Если на систему действуют одни только консервативные силы, то можно для нее ввести понятие потенциальной энергии.

Работа, совершаемая консервативными силами при переходе системы из рассматриваемого в нулевое положение называется разностью потенциальных энергий в рассматриваемом и нулевом положениях. Работа консервативных сил не зависит от пути перехода, а потому потенциальная энергия системы E_п является функцией только ее координат.

Потенциальная энергия системы определена не однозначно, а с точностью до произвольной постоянной. Этот произвол не может отразиться на физических выводах, так как ход физических явлений может зависеть не от абсолютных значений самой потенциальной энергии, а лишь от ее разностей в различных состояниях. Эти же разности от выбора произвольной постоянной не зависят.

Пусть система перешла из положения 1 в положение 2 по какому-либо пути 12. Работу A₁₂, совершенную консервативными силами при таком переходе, можно выразить через потенциальные энергии E_п1 и E_п2 в состояниях 1 и 2:

,

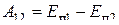т. е. работа консервативных сил равна убыли потенциальной энергии системы.

Та же работа А₁₂ может быть выражена через приращение кинетической энергии по формуле .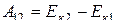

Приравнивая последние два выражения, получим 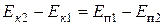, откуда

.

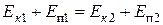Сумма кинетической и потенциальной энергий системы называется ее полной энергией Е. Таким образом, 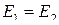 или

.

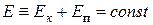В системе с одними только консервативными силами полная энергия остается неизменной. Могут происходить лишь превращения потенциальной энергии в кинетическую и обратно, но полный запас энергии системы измениться не может. Это положение называется законом сохранения энергии в механике.

Вычислим потенциальную энергию в некоторых простейших случаях.

а) Потенциальная энергия тела в однородном поле тяжести. Если материальная точка, находящаяся на высоте h, упадет на нулевой уровень (т. е. уровень, для которого h = 0), то сила тяжести совершит работу. Поэтому на высоте h материальная точка обладает потенциальной энергией 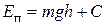. За нулевой можно принять произвольный уровень, например, уровень пола (если опыт производится в лаборатории), уровень моря и т. д. Постоянная С равна потенциальной энергии на нулевом уровне. Полагая ее равной нулю, получим

.

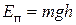б) Потенциальная энергия растянутой пружины. Упругие силы, возникающие при растяжении или сжатии пружины, являются консервативными силами. Поэтому имеет смысл говорить о потенциальной энергии деформированной пружины. Ее называют упругой энергией. Обозначим через х растяжение пружины, т. е. разность 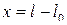 длин пружины в деформированном и недеформированном состояниях. Упругая сила F зависит только от растяжения. Если растяжение х не очень велико, то она пропорциональна ему: F = kx (закон Гука). При возвращении пружины из деформированного в недеформированное состояние сила F совершает работу

.

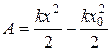Если упругую энергию пружины в недеформированном состоянии условиться считать равной нулю 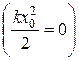, то

.

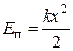в) Потенциальная энергия гравитационного притяжения двух материальных точек. По закону всемирного тяготения Ньютона гравитационная сила притяжения двух точечных тел пропорциональна произведению их масс Mm и обратно пропорциональна квадрату расстояния между ними:

,

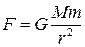где G – гравитационная постоянная. Силы гравитационного притяжения являются консервативными. Для них имеет смысл говорить о потенциальной энергии. При вычислении этой энергии одну из масс, например М, можно считать неподвижной, а другую – перемещающейся в ее гравитационном поле. При перемещении массы т из бесконечности гравитационные силы совершают работу

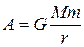
где r – расстояние между массами М и m в конечном состоянии. Эта работа равна убыли потенциальной энергии:

.

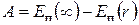Обычно потенциальную энергию в бесконечности U(¥), принимают равной нулю. При таком соглашении

.

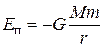Данная величина отрицательна. Это имеет простое объяснение. Максимальной энергией притягивающиеся массы обладают при бесконечном расстоянии между ними. В этом положении потенциальная энергия считается равной нулю. Во всяком другом положении она меньше, т. е. отрицательна.

Вопросы для самоконтроля:

1. Сформулируйте определение работы силы. В каких единицах измеряется работа?

2. При каких условиях работа силы положительная? отрицательная? равна нулю?

3. Дайте определение мощности. В каких единицах измеряется мощность?

4. Сформулируйте определение энергии. В каких единицах измеряется энергия?

5. Что является мерой изменения энергии систем тел?

6. Дайте определение кинетической энергии тела.

7. Сформулируйте теорему о кинетической энергии.

8. Какие силы называются консервативными? Приведите примеры.

9. Чему равна работа, совершаемая упругой силой? гравитационной силой?

10. Чему равна потенциальная энергия упругодеформированного тела?

11. Чему равна полная механическая энергия системы тел?

12. При каких условиях полная механическая энергия системы сохраняется?