Структурная схема устройства ЧАПЧ непрерывного типа соответствует обобщенной схеме АПЧ, приведенной на рис. 2. Частотный дискриминатор приведен на рис. 4.

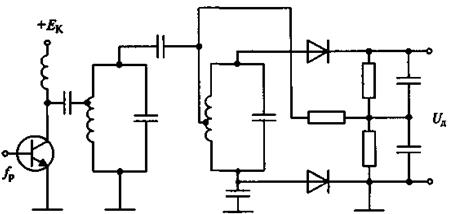
Рис. 4 – Частотный дискриминатор балансного типа

В ней под звеном сравнения следует понимать частотный дискриминатор, напряжение, на выходе которого зависит от частоты на его входе. Известно несколько схем частотных дискриминаторов, наиболее распространенными из которых являются схемы балансного типа (рис. 4) и на расстроенных контурах.

В качестве частотного дискриминатора может использоваться и микросхема, имеющая два входа (рис. 5, а). На 1-й вход подается сигнал частоты f₀, определяющий среднюю частоту дискриминатора, а на 2-й - сигнал разностной частоты f _р = f _ст – f _эт. При f_p > f ₀ напряжение на выходе дискриминатора и_д= U _д, а при f_p < f ₀ напряжение и_д=– U _д. В результате характеристика дискриминатора имеет вид, приведенный на рис. 5, б.

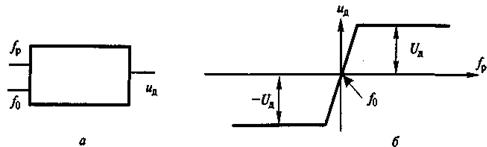
Рисунок 15.5. Характеристика дискриминатора

Из схем управления частотой автогенератора выделим две: с варикапом и ферритом. Варикапом называется полупроводниковый диод, емкость закрытого р-n-перехода которого существенно зависит от значения обратного напряжения U _обр. Данная зависимость определяется следующим примерным соотношением:

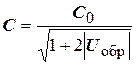.                                          (1)

Схема управляющего элемента с варикапом приведена на рис. 6.

Рис. 6 – Схема управляющего элемента с варикапом

Схема управляющего элемента с ферритом показана на рис. 7. Катушка индуктивности с ВЧ ферритом располагается в зазоре электромагнита. При изменении тока подмагничивания меняется дифференциальная магнитная проницаемость феррита, что приводит к измерению индуктивности контура и частоты автоколебаний.

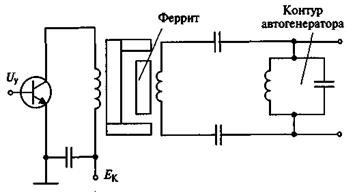
Рис. 7 – Схема управляющего элемента с ферритом

В обеих схемах характеристика управляющего элемента D f_y = y ( U_y) подобна характеристике, приведенной на рис. 3, б.

В качестве ФНЧ может использоваться однозвенный RC - фильтр (рис. 8).

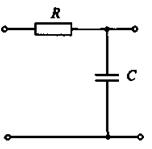
Рис. 8 – Однозвенный RC-фильтр

Определим точность ЧАП в установившемся режиме работы, в котором линейная модель устройства описывается системой из трех уравнений:

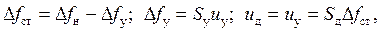                 (2)

где D f _ст - отклонение частоты стабилизируемого автогенератора от номинального значения; D f _н - начальная расстройка того же автогенератора; D f_y- изменение частоты автогенератора под действием управляющего элемента в замкнутой системе. (Остальные параметры определены выше на рис. 3.). Решив совместно уравнения (2), получим уравнение для отклонения частоты стабилизируемого автогенератора в установившемся режиме работы:

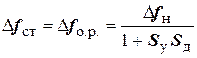,                        (15.3)

где D f _о.р. - остаточная расстройка.

Из (3) следует, что благодаря действию устройства ЧАПЧ первоначальное отклонение частоты стабилизируемого автогенератора от номинального значения D f _н уменьшается в К_рег=(1+S_уS_д) раз. Поскольку коэффициент авторегулирования К_рег>>1, то это уменьшение может быть весьма существенным - в 1000 и более раз. Графическое решение уравнений (2) представлено на рис. 9. Из него также следует, что решением уравнений (2) является величина D f _ст = D f _о.р.. Именно на эту величину, которая определяет точность ЧАПЧ, отличается частота стабилизируемого автогенератора от номинального значения в установившемся режиме.

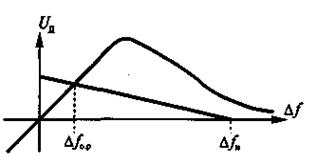
Рис. 9 – Графическое решение уравнений (2)

Пример. Начальная расстройка Df_н=000 кГц. Крутизна S_y=400 кГц/В, крутизна S_д=5 В/кГц. Коэффициент регулирования К_рег=1+S_уS_д=2001. Остаточная расстройка Df_о.р.=Df_н/К_рег=0,5 кГц. Таким образом, нестабильность частоты стабилизируемого автогенератора с 1000 кГц уменьшается до 500 Гц.