Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

КОНТРОЛЬНАЯ РАБОТА № 2

Расчет цепей с источниками гармонических воздействий

Задание

1. По заданному номеру варианта изобразить цепь, подлежащую расчету, выписать значения параметров элементов.

Записать в общем виде систему уравнений Кирхгофа для полученной цепи.

Рассчитать токи во всех ветвях и напряжение на источнике тока методом контурных токов.

Составить баланс активных и реактивных мощностей.

Записать мгновенные значения токов ветвей и напряжение на источнике тока.

Рассчитать токи во всех ветвях и напряжение на источнике тока методом узловых потенциалов.

Рассчитать ток одной ветви методом эквивалентного генератора.

Найти ток одной ветви методом наложения.

Определить потенциалы всех точек цепи и построить на комплексной плоскости векторную топографическую диаграмму напряжений и токов.

2.2. Выбор варианта цепи

1. Граф цепи, подлежащей расчету, выбирать в соответствии с рис. 2.1. Расположение источников напряжения и тока, а также пассивных элементов в ветвях выбирать с помощью табл. 2.1. Направление действия источников произвольное.

2. Численные значения параметров источников напряжения и тока выбирать с помощью табл. 2.2. Частота питающего напряжения и тока f=50 Гц.

3. Численные значения параметров пассивных элементов определяются по формулам:

для четных ветвей:	для нечетных ветвей:
R = R0 + AR · N ,	R = R0 + AR · 3,5N,
L = L0 + AL · N ,	L = L0 + AL · 3,5N,
C = C0 + AC · N ,	С = С0 + AС · 3,5N,

где N – номер группы, значения коэффициентов R₀, L₀, C₀ заданы в табл. 2.3, а каждый из дополнительных коэффициентов A_R, A_L, A_C, имея соответствующую размерность (Ом, мГн, мкФ), равен сумме цифр номера варианта.

 

 

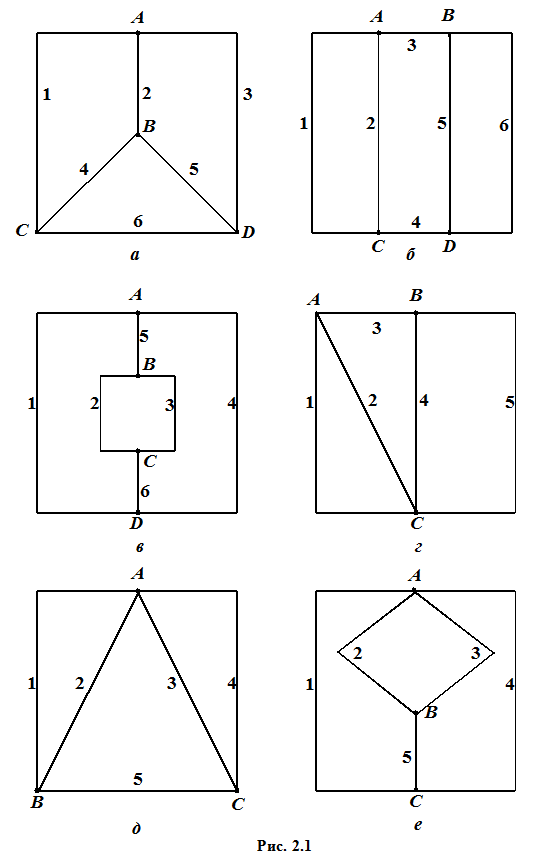
Таблица 2.1

Номер

варианта

Граф

Расположение элементов в ветвях цепи

источник напряже-ния источ-ник тока резисторы индуктив-ности емкости 1, 26, 51, 76 а 1 3 2, 3, 4, 5, 6 2 6 2, 27, 52, 77 б 1 5 1, 2, 3, 4, 5, 6 1 4 3, 28, 53, 78 в 3 6 1, 2, 4, 5, 6 4 1 4, 29, 54, 79 г 5 1 1, 2, 3, 4, 5 3 5 5, 30, 55, 80 д 5 3 1, 2, 3, 4, 5 2 3 6, 31, 56, 81 е 5 4 1, 2, 3, 4, 5 1 4 7, 32, 57, 82 а 3 6 1, 2, 4, 5, 6 1 2 8, 33, 58, 83 б 5 1 1, 2, 3, 4, 5,6 4 2 9, 34, 59, 84 в 4 1 1, 2, 3, 5, 6 2 6 10, 35, 60, 85 г 5 4 1, 2, 3, 4, 5 1 3 11, З6, 61, 86 д 1 3 1, 2, 3, 4, 5 2 5 12, 37, 62, 87 е 4 1 1, 2, 3, 5 2 3 13, 38, 63, 88 а 2 1 1, 3, 4, 5, 6 1 3 14, 39, 64, 89 б 4 3 1, 2, 3, 4, 5,6 2 5 15, 40, 65, 96 в 6 4 1, 2, 3, 4, 5 1 5 16, 41, 66, 91 г 1 5 1, 2, 3, 4, 5 3 4 17, 42, 67, 92 д 3 4 1, 2, З, 4, 5 1 3 18, 43, 68, 93 е 5 3 1, 2, 3, 4, 5 4 2 19, 44, 69, 94 а 2 3 1, 3, 4, 5, 6 5 1 20, 45, 70, 95 б 3 5 1, 2, 3, 4, 5, 6 1 2 21, 46, 71, 96 в 1 3 2, 3, 4, 5, 6 2 6 22, 47, 72, 97 г 3 5 1, 2, 3, 4, 5 4 2 23, 48, 73, 98 д 2 5 1, 2, 3, 4, 5 3 2 24, 49, 74, 99 е 3 2 1, 2, 4, 5 5 1 25, 50, 75, 100 а 5 4 1, 2, 3, 4, 6 3 4

 

 

Таблица 2.2

Ветви

Е

J

АТ, АТПП, КТЭИ, АД, ЭТМ АЭП, ТК, ИВК ПКМ, ТТУМ, ОНГП АСУ, ЭС, АТП, ТПМП, ТЦБП АТ, АТПП, КТЭИ, АД, ЭТМ АЭП, ТК, ИВК ПКМ, ТТУМ, ОНГП АСУ, ЭС, АТП, ТПМП, ТЦБП 1 50e^{–j60 °} 150e^{j30 °} 200e ^{j0 °} 3e^{j45 °} 4e^{j150 °} 5e^{j150 °} 2 100e^{–j45 °} 100e^{j60 °} 150e ^{–j45 °} 2e^{j60 °} 5e^{j0 °} 4e^{j45 °} 3 120e ^{j30 °} 200e^{j45 °} 100e ^{–j45 °} 5e^{–j45 °} 3e^{–j120 °} 2e^{j30 °} 4 141e ^{j0 °} 50e^{–j30 °} 141e ^{–j60 °} 4e^{–j30 °} 4e^{–j60 °} 3e^{j0 °} 5 150e ^{j45 °} 200e ^{–j45 °} 141e ^{j45 °} 3e^{–j60 °} 5e^{–j45 °} 5e^{–j60 °} 6 100e ^{–j90 °} 120e ^{–j60 °} 150e ^{j150 °} 2e^{j45 °} 4e^{–j150 °} 3e^{j120 °}

Таблица 2.3

	R 0 , Ом	L 0 , мГн	С О , мкФ
АСУ, ТЦБП	40	80	100
АT, АД, АТПП	50	100	110
АЭП, ИВК, ТПМП	60	120	120
КТЭИ, ЭТМ	70	140	130
ТК, ТТУМ	80	160	140
ЭС, ОНГП	90	180	150
АТП, ПКМ	100	150	160

Методические указания

Метод уравнений Кирхгофа

1. Пронумеровать m ветвей и обозначить n узлов в соответствии с графом цепи.

Обозначить токи ветвей и произвольно выбрать их положительное направление, а также выбрать полярности на зажимах источника тока.

3. Произвольно выбрать опорный узел и для прочих (n – 1) узла записать уравнения по I закону Кирхгофа в форме

.

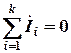Алгебраическая сумма токов в любом узле электрической цепи равна нулю. При суммировании токи, направленные к узлу, следует принять условно положительными, а направленные от узла – отрицательными (или наоборот).

4. Произвольно выбрать совокупность p независимых контуров и обозначить направление их обхода. Для каждого из независимых контуров записать уравнения по II Закону Кирхгофа в форме

.

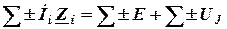При суммировании в левой части положительными принимают падения напряжения на тех потребителях, в которых выбранное положительное направление тока совпадает с направлением обхода контура; в правой части положительными принимают ЭДС источников, являющихся содействующими в смысле выбранного направления обхода контура (потенциал на них возрастает).

Метод контурных токов

Применение метода позволяет уменьшить общее количество уравнений системы до числа независимых контуров p.

Баланс мощностей

Или

,

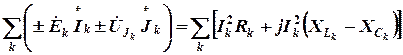где 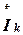– сопряженный комплекс тока k -й ветви;

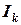     – действующее значение тока k -й ветви;

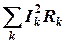     – активная мощность потребителей;

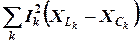     – реактивная мощность потребителей.

Выражение в левой части равенства представляет собой суммарную комплексную мощность источников. Правило знаков аналогично изложенному в п. 3.4 (контрольная работа № 1).

Метод узловых потенциалов

Применение данного расчетного метода позволяет уменьшить количество уравнений системы до (n – 1), где n – число узлов электрической цепи. Порядок расчета данным методом следующий:

1. Потенциал одного из узлов (любого) условно принять равным нулю. Этот узел называют опорным.

2. Для расчета неизвестных (n – 1) потенциалов составить систему уравнений, записываемую в виде матричного уравнения вида

,

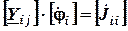где  – квадратная матрица комплексных проводимостей, в которой:

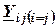        – собственная комплексная проводимость, определяемая как сумма проводимостей ветвей, сходящихся в узле;

 – общая комплексная проводимость ветвей, соединяющих i и j узлы, определяемая как проводимость ветви, соединяющей i и j узлы. В случае, если между i и j узлами подключены несколько ветвей (не имеющих промежуточных узлов), общая проводимость определяется как сумма проводимостей ветвей, соединяющих узлы. Общая проводимость в системе уравнений всегда берется со знаком минус.

В н и м а н и е! Проводимость ветви, содержащей источник тока, равна 0.

Д о п о л н е н и е. Для цепей, в ветвях которых подключены только идеальные источники напряжения (R_ветви = 0), расчет может быть упрощен при выборе опорного узла на выводах этих ветвей. Тогда потенциал одного из узлов становится известным и равным ЭДС идеального источника напряжения. Таким образом, количество совместно рассматриваемых уравнений системы сокращается. Однако следует отметить, что оставшиеся уравнения остаются неизменными, т.е. содержат слагаемые, являющиеся произведением известного потенциала узла и соответствующей проводимости.

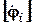 – матрица-столбец потенциалов;

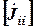– матрица-столбец узловых токов, определяемых по следующей формуле:

,

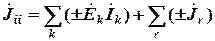Метод наложения

Решение задач данным методом основано на применении принципа суперпозиции (наложения), согласно которому ток в произвольной i-й ветви равен алгебраической сумме токов, создаваемых каждым источником в отдельности.

При расчете цепей методом наложения из исходной цепи получают k вспомогательных схем (подсхем), где k – число источников. В каждой из этих вспомогательных схем оставляют только один источник. Удаление источников осуществляется в соответствии со следующим правилом: источники ЭДС заменяются короткозамкнутыми участками, ветви с источниками тока размыкаются. В каждой из полученных подсхем рассчитываются составляющие соответствующих токов, создаваемые данным источником. Токи исходной цепи определяются как алгебраическая сумма соответствующих токов вспомогательных схем:

.

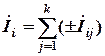Пример расчета

Задание

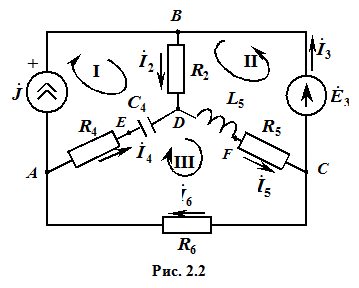
Рассчитать цепь, изображенную графом а (рис. 2.1), в которой

E = 150е^j30; J = 3e^j45; f = 50 Гц.

Параметры пассивных элементов:

R ₂ = R₄ = R₆ = 38 Oм;

R ₅ = 66 Oм;

L ₃ = 176 мГн;   X_L5 = 2 p fL = 55,292 Ом;

C ₄ = 136 мкФ;  X_C4 = 1/(2 p fC ) = 23,405 Ом.

Подлежащая расчету схема имеет вид, представленный на рис. 2.2:

Число узлов n = 4. Число независимых контуров p = 3.

2.4.2. Составление системы уравнений Кирхгофа

Произвольно задавшись положительным направлением токов ветвей (см. рис. 2.2) и совокупностью независимых контуров, запишем:

– уравнения по I закону Кирхгофа, число уравнений (n – 1) = 4 – 1 = 3

узел А : ;

узел В: ;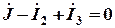

узел С: .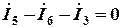

– уравнения по II закону Кирхгофа, число уравнений p = 3,

I контур: ;

II контур: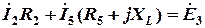

I II контур: .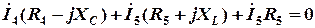

В результате имеем систему, состоящую из 6 уравнений, разрешимую относительно 6 неизвестных: _.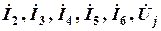

Определители системы:

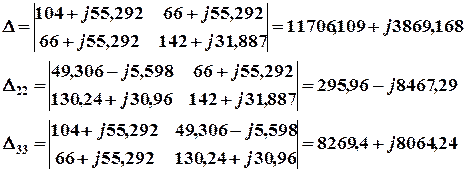
Ток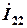и   и 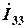 находят по формулам:

,

.

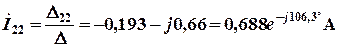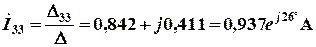В соответствии с условно принятыми положительными направлениями (см. рис. 2.2) вычислим токи ветвей:

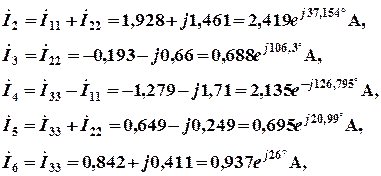
Мгновенные значения токов ветвей и напряжения на источнике тока

Поскольку угловая частота равна w = 2 p f , а амплитуда связана с действующим значением с помощью соотношения 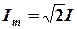, следовательно,

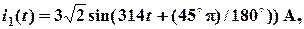
где  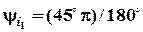    - начальная радиан-фаза тока i₁ ,

аналогично запишем:

 

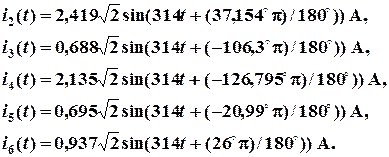
Метод наложения

С использованием принципа суперпозиции рассчитывается ток 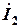. Поскольку в цепи два источника, для определения искомого тока строятся две подсхемы, каждая из которых содержит только один из источников, а второй исключается в соответствии с правилом, изложенным в п.п. 3.4.

Расчет составляющей 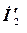 по схеме (рис. 2.7)

.

.

 

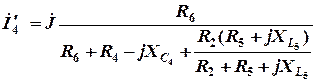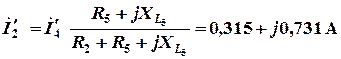Расчет составляющей 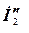 по схеме (рис. 2.8)

.

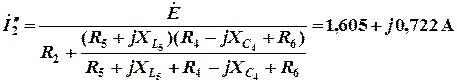Искомый ток

.

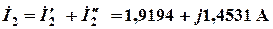Напряжение холостого хода

.

Определение входного сопротивления пассивного двухполюсника (рис. 2.10)

.

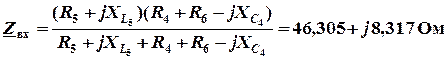C учетом 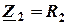 искомый ток .

 

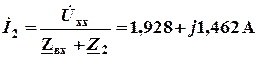Библиографический список

Приложение 1

Министерство образования РФ

Пермский государственный технический университет

Контрольная работа № 1

Вариант №

 

	Выполнил студент гр. (№ зачетной книжки ) (Ф.И.О.)
	Проверил преподаватель каф. КРЭС (Ф.И.О.)

 

 

Пермь 20 10

 

КОНТРОЛЬНАЯ РАБОТА № 2

Расчет цепей с источниками гармонических воздействий

Задание

1. По заданному номеру варианта изобразить цепь, подлежащую расчету, выписать значения параметров элементов.