Основан на измерении удельного электрического сопротивления и магнитной проницаемости горных пород.
В некоторых случаях электрическое сопротивление пород в зонах трещиноватости отличается в несколько раз от значения в нарушенном массиве.
Геодезические методы обеспечены необходимой аппаратурой, методиками и широко применяется на практике.
Реометрические методы.
Основаны на измерении скорости падения давления сжатого воздуха или воды в скважинах или шпурах, пробуренных в породах окружающих выработку.
Схема метода
1-выработка
2-скважина (шпур)
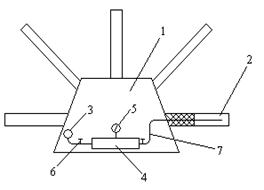3-магистраль сжатого воздуха
4-резервуар сжатого воздуха
5-манометр
6-вентили
7-шланг
8-герметизатор
(из вакуумной резины)
Герметизирующие устройства при нагнетании сжатого воздуха устанавливаются на различных расстояниях от устья. Падение давления измеряется манометром.
При нагнетании воды определяется расход воды и время, через которое она появляется на контуре или в соседней скважине (шпуре).
Степень нарушенности пород оценивают коэффициентом проницаемости:
Кпр=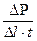 
,
где: ∆ P - величина падения давления на участке скважине (шпуре),
∆ l -длина части шпура, находящегося под давлением,
t- время падения давления.
Акустический метод оценки трещиноватости основан на сопоставлении скоростей продольных волн в массиве и отдельности. Методика таких измерений разработана в МГИ, а степень трещиноватости оценивают по акустическому показателю трещиноватости, определяемому величиной отношения квадратов скоростей продольных волн в образце и в массиве.
Степень трещиноватости не является абсолютной характеристикой и может изменяться в результате воздействия на массив различных факторов, из которых наиболее существенным является влияние предшествующих взрывов.
После взрыва .поверхность массива нарушается трещинами-заколами, которые обычно параллельны бровке уступа. При вертикальных зарядах зона заколообразования по кровле уступа составляет около 100 диаметров заряда d , а вдоль оси заряда в глубь массива (7-10d).
Граница между нарушенным массивом и целиком может быть установлена различными методами: по изменению скорости утечки воды из скважины, падению давления сжатого воздуха в пробуренном шпуре и т.д.
Однако все эти методы дают только качественную оценку данного участка.
Контрольные вопросы:
1. Назовите особенности физических методов оценки трещиноватости.
2. Охарактеризуйте методы непосредственных замеров.
3. Определите точность косвенных методов оценки.
4. Перечислите и дайте оценку физическим методам оценки трещиноватости.
5. Что такое каротаж и какие методы каротажа можно назвать?
Модуль 2. Изучение трещиноватости и механических свойств горных пород
Раздел 4. Оценка структурного ослабления массива горных пород. Особенности деформирования и разрушения массива
Тема 5. Оценка структурного ослабления массива горных пород. Особенности деформирования и разрушения массива
ЛЕКЦИЯ № 7
План лекции
1. Характеристики ослабления массива.
2. Виды воздействия нарушений на массив.
3. Структурное ослабление массива.
4. Механические свойства пород.
Структурное ослабление горных пород
Структурная неоднородность массива горных пород проявляется в его прочностных и деформационных свойствах двояко: непосредственно и опосредственно (косвенно). Если размеры исследуемого объема пород (или объекта в массиве пород) соразмерны с величиной структурного блока i-го масштабного уровня, то:
♦ разрывные нарушения i-го, (i - 1)-го и т.д. масштабных уровней будут влиять на состояние и свойства массива непосредственно;
♦ разрывные нарушения (i+1)-го, (i+2)-го и т.д. масштабных уровней косвенно влияют на состояние и свойства массива или объекта.
При этом линейные параметры объекта и структурного блока будем считать соразмерными, если их соотношения не удовлетворяют ранее установленному условию Lоб/Lcтр не менее 10 - 20 или хотя бы условию не менее 5,5 - 6,5.
Междукамерный или потолочный целик с линейными размерами в наименьшем поперечном сечении около 10 м будет испытывать непосредственное воздействие разрывных нарушений (трещин) I и II масштабных уровней и косвенное — III масштабного уровня.
Разумеется, схемы воздействия разрывных нарушений на массив (или объект в массиве) имеют определенную условность. Вследствие этого в рассматриваемом примере и в пределах i-го (в нашем случае II) масштабного интервала возможны разрывные трещины, влияние которых на объект окажется косвенным (особенно, если размеры объекта и структурного блоки таковы, что они приурочены соответственно к противоположным границам зоны).
Непосредственное воздействие разрывного нарушения проявляется в том, что это нарушение (тектоническая трещина, дайка и т.п.), имеющее конечную ширину раскрытия, пересекает исследуемый массив или объект полностью и образует в нем аномальную по прочностным и деформационным характеристикам область. Поскольку прочностные свойства среды вдоль этой области, как правило, на порядок и более ниже соответствующих в массиве, объект деформируется и разрушается непосредственно вдоль этого нарушения при напряженных состояниях, существенно допредельных для остального окружающего разлом массива.
Влияние таких разрывных нарушений на состояние массива или объекта учитывается индивидуально путем изучения ряда характеристик прочностных и деформационных свойств на поверхности разлома (если он зияющий) или свойств среды-заполнителя (если он заполнен вторичными материалами); геометрических параметров разлома и соотношения их с параметрами объекта; взаимной ориентировки направлений поверхности разлома и действующих в массиве усилий.
Косвенное воздействие разрывных трещин на объект проявляется при соотношениях Lоб/Lcтр более 5,5 и заключается в снижении прочности массива пород и изменении характера его деформирования. В этом случае учет влияния трещин на состояние массива или объекта производится по совокупности путем изучения одновременного влияния всех имеющихся систем трещин на прочностные и деформационные свойства массива пород.
Изучение и учет непосредственного влияния разрывных нарушений на массив или сооружение в нем не представляют существенных затруднений как в методическом, так и техническом отношениях. Они сводятся к определению взаимной ориентировки поверхностей трещины и обнажений массива пород; оценке взаимоотношении направлении и величин приложенных усилий с прочностными характеристиками заполнителя. В литературе эти вопросы описаны достаточно подробно. Значительно большие трудности возникают при изучении косвенного влияния трещинной структуры массива на его состояние и свойства.
Характерной особенностью горных пород является их высокая хрупкость. Она обусловлена тем, что на различных масштабных уровнях массивы горных пород представляют собой сложную структурную среду, у которой сцепление между элементами (зернами, структурными блоками) существенно меньше, чем в самих элементах.
Хрупкие материалы отличаются весьма низким сопротивлением растяжению (отрыву). Этим объясняется свойство горных пород разрушаться в форме отрыва при самых различных напряженных состояниях, в том числе и при всестороннем неравномерном сжатии. Анализируя характер разрушения образцов пород и опорных целиков, Г.Л. Фисенко отмечает, что даже в случае, когда разрушение происходит в виде косого среза, ему предшествует начальное разрушение в виде разрыва по направлению, нормальному в приложенной сжимающей нагрузке. Наши наблюдения показали, что во всех случаях разрушение разрыва образцов зарождается и развивается в местах имеющихся трещин, микротрещин и других дефектов однородности.
При разрушении твердых тел кроме разрыва широко распространены деформации среза (сдвига). Г.Л. Фисенко считает, что деформирование и разрушение горных пород в массиве происходят в определенной последовательности: сдвиг в упругой стадии — отрыв — разрушение слабых блоков — поворот более прочных структурных блоков. Эти выводы основаны на предпосылке о характере деформирования трещиноватого массива. Если направление приложения усилия не совпадает с плоскостями трещин, то происходит деформация растяжения в направлении наименьшего главного напряжения, появляются трещины отрыва. После этого в наиболее слабых участках структурных блоков, ограниченных трещинами разрыва, появляются сколовые трещины. Затем происходит вращательное перемещение структурных блоков. Именно разворотструктурных элементов под нагрузкой имеет решающее значение в формировании прочности структурированных массивов пород.
 |
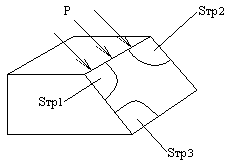Прочность массива на сдвиг (разрыв) в значительной степени определяется наличием трещин вдоль линии сдвига(разрыва).
Sтр1,2,3-площади сдвига по трещинам
P- срезающее усилие.
См∙S=Стр∙∑Sтрi+Ск(S-∑ Sтрi),
Где См - сцепление пород в массиве
Ск - сцепление пород в куске(образце)
Стр - сцепление пород по трещинам
S - общая площадь сдвига
Sтрi - суммарная площадь трещин.
Коэффициент структурного ослабления:
Кстр =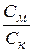 
С-предел прочности на срез или сдвиг
Кстр= 0,2-0,4
Пример: По данным ВНИМИ для апатитовых месторождений С=3,0 МПа, Стр=0,3-площадь межтрещенных участов-30%,трещин-70%. Тогда См∙1=0,3∙0,7+3∙0,3; См=1,1 МПа
Кстр=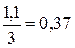 
Для определения коэффициента структурного ослабления (Кстр) проводят лабораторные испытания на образцах и крупномасштабные дорогостоящие натурные испытания. требующие специального оборудования. Поэтому натурные испытания доступны в основном крупным предприятиям.
В большинстве случаев проводят лабораторные испытания руд и пород, а их результаты корректируют с помощью “Кстр”, полученного наружными испытаниями в сходных условиях.
Факторы, влияющие на “Кстр”
Кстр = f (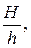 
λ, f, C, Y, V)
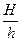- количество элементарных боков, слагающих элемент конструкции;
H-элемент в натуре;
h - размер элементарного блока;
λ - угол падения определенных трещин;
f - коэффициент крепости пород;
C-сцепление;
Y – угол внутреннего трения (ширина трещин, минеральный заполнитель, шероховатость стенок, волокнистость);
V - характер напряженного состояния (одноосное, объемное).
Механические свойства пород
Прочностные, деформационные, физико-технические.
Прочностные свойства определяют падение пород в различных условиях (пределы прочности на растяжение, сжатие, изгиб, срез со сжатием длительная прочность, хрупкость, пластичность, вязкость)
Деформационные свойства определяют способность породы деформироваться, в том числе при длительном напряжении (упругость, ползучесть, релаксация).
Испытание свойств пород.
Испытание предусматривает подготовительный период, который включает 4 этапа:
§ Выбор места отбора проб
§ Отбор проб
§ Консервация и транспортировка
§ Изготовление образцов
В качестве проб отбирают породные блоки с размерами е менее 0,2×0,2×0,2м или керны диаметром от 40 до 90 мм длиной от 70 мм.
Отобранные пробы тщательно документируют. Пробы мягких пород консервируют, заворачивая в бумагу, пропитанную парафином или двумя слоями пропарафиненной ткани.
Образцы изготавливаю с применением специального бурового или камнерезного оборудования.
Полученный размер образа должен быть не менее 7-9 зернам(≥40-50мм).
Недостатки натурных исследований:
§ трудность проведения;
§ неудовлетворенная обработка поверхностей испытуемых тел, выделенных в массиве;
§ относительно малые размеры испытуемого объекта;
§ обычно небольшое число опытов.
Недостатки лабораторных исследований.
§ несовершенство методики отбора образцов и методики испытания прочностных и деформационных характеристик ;
§ ограниченность числа мест отбора образцов всегда являются достаточно представительны ;
§ отбор проб в выработках приводит к тому, что испытания образцов ведутся уже при повторных нагрузках;
§ пробы, не смотря на парафинирование в процессе транспортировки, хранении, изготовлении образцов изменяют естественную влажность;
§ при отбое проб и изготовлении образцов неизбежно отбираются наиболее прочные части, поскольку наиболее слабые , трещиноватые и имеющие другие дефекты разрушаются;
§ при испытании образцов трудно избежать перекосов вследствие неточности обработки проб, несоосности приложения нагрузок, влияния концентрации напряжений в метах приложения захватов и др.
Испытание на одноосное сжатие
 |
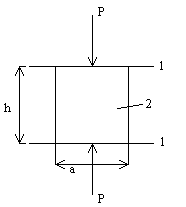1-плита пресса
2-образец
P- разрушающая нагрузка
.
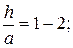
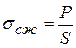Предел прочности пород на одноосное сжатие - одна из наиболее важных механических характеристик горных пород. Профессор Протодьяконов (1926) разделил горные породы по крепости на классы от 1 до 20 (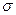 
сж изменяется от 10 до 200МПа). Крепкие кварциты, крепкие базальты, диабазы 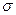сж=400-500МПа. Корундовые породы-до800МПа.
Условия испытания
1-сухое трение;
2-со смазкой торцов (имитируется наличие пластичных прослоек на торцах).
Предел прочности одной и той же горной породы имеет различные значения в зависимости от способа нагружения (режима испытания), вида напряженного состояния и некоторых других факторов.
На практике чаще всего определяют показатели стандартной прочности, получаемой при испытании образца породы стандартного размера и формы и в режиме, регламентированном техническими условиями и инструкциями. Основными показателями стандартной прочности является временные сопротивления сжатию (σсж), растяжению (σр) и сдвигу (σсдв), т.е. пределы прочности при указанных напряженных состояниях. Наибольшие числовые значения имеют временные сопротивления на сжатие, наименьшие – на растяжение.
Контрольные вопросы:
1. Каким образом структурная неоднородность влияет на свойства горных пород?
2. Перечислите схемы воздействия разрывных нарушений на массив.
3. Охарактеризуйте механизм разрушения хрупких пород.
4. Перечислите недостатки натурных наблюдений.
5. Как имитируются пластичные прослойки при испытаниях образцов?
Модуль 2. Изучение трещиноватости и механических свойств горных пород
Раздел 5. Деформирование и разрушение горных пород. Прочностные, деформационные и реологические свойства горных пород
Тема 6. Механические свойства горных пород и массивов
ЛЕКЦИЯ № 8
План лекции
1. Прочностные и деформационные свойства пород.
2. Прямые и косвенные методы определения механических свойств.
Механические свойства относятся к числу физических характеристик горных пород, используемых при решении важнейших научных и практических задач горного дела: определения силовых и энергетических параметров процесса разрушения горных пород, прогнозе проявлений горного давления и установлений тональных способов управления ими и многих др.
Механические свойства характеризует сопротивляемость породы разрушению и деформациям. Соответственно различают прочностные деформационные свойства горных пород.
Прочностные свойства обычно оценивают максимальной нагрузкой, воспринимаемой образцом горной породы до разрушения и называемой пределом прочности. Такое представление о прочности связано с критическим характером процесса разрушения горной породы: потеря сплошности (т.е. разрушение) наступает, когда один из параметров, определяющих состояние деформируемого образца горной породы, например, нормальное (σn) или касательное напряжение (τ), достигает предельного, критического значения.
Предел прочности одной и той же горной породы имеет различные значения в зависимости от способа нагружения (режима испытания), вида напряженного состояния и некоторых других факторов.
Испытания в условиях сухого трения
Форма образца кубическая, призматическая и цилиндрическая.
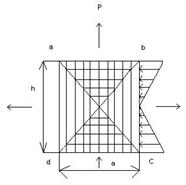
Эпюра, эквивалентная сигнал трения по высоте образца
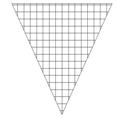Зона объемного напряженного состояния
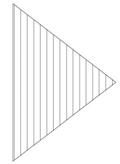Зона одноосного сжатия
При сжатии образца точки abcd сохраняют первоначальное положение. Образец приобретает бочкообразную форму.
В пределах образца возникают зоны объемного напряженного состояния под влиянием сил трения и переферийные зоны одноосного сжатия.
Разрушения начинаются под влиянием растягивающих деформаций с образованием вертикальных трещин и заканчивается образованием наклонных линий скольжения.
Образуется два стыкующихся конуса, напоминающих песочные часы. С изменением высоты образца зоны объемного напряженного состояния сдвигаются по высоте или накладываются.
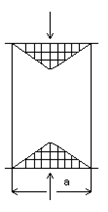
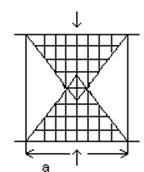
С увеличением высоты образца несущая способность уменьшается и может быть выражена в уравнении:
Кф=1,15-0,15 
,
где Кф- коэффициент формы
Испытание при отсутствии трения на торцах
Во всех случаях при нагружении уменьшается высота образца и увеличивается ширина.
Разрушение происходит за счет растягивающих деформаций с образованием вертикальных трещин. С увеличением высоты образца несущая способность снижается.
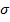сж = 
Испытание на растяжение
Прямой метод
Вследствие сложности изготовления образцов, сложности проведения эксперимента и получение заниженных результатов этот метод не применяется.
Косвенные методы (раскалывание образца).
а) б)
в) 
 |
Испытания пород на срез (одноплоскостной и двухплоскостной) с одновременным приложением различной по величине нормальной сжимающей нагрузки дают наиболее надежные результаты. Схема испытаний на срез со сжатием в наклонных матрицах показана на рисунке. Испытательное устройство состоит из трех пар сменных матриц с углом наклона, равным 30, 45 и 60°, двух разрезных обойм-вкладышей 2, двух плит 3 и роликового опорного приспособления 4. Пресс создает вертикальную нагрузку, которая в образце автоматически раскладывается на две составляющие: нормальную к плоскости среза и срезающую. Зная максимальное значение разрушающей нагрузки Fmax, вычисляют предельное нормальное и касательное напряжения на плоскость среза по формулам
1-полуматрицы
2-образец
3-диски
4-система роликов
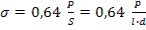
σн 
σ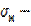 
нормальная составляющая напряжения
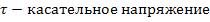
τ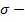 
главное напряжение
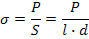
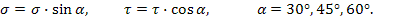
Предельное значение развиваемого при срезе касательного напряжения соответствует пределу прочности при срезе.
Испытания на срез со сжатием в наклонных матрицах можно проводить на образцах правильной и неправильной формы.
Графическое представление результатов испытаний
τ 
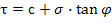
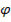С-сцепление
σ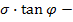 
сила трения
Испытания в объемном напряженном состоянии
(в стабилометре).
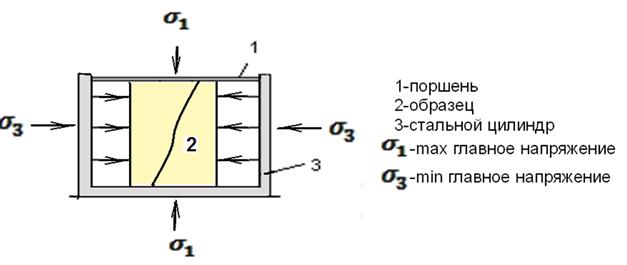
Прочность горной породы при двухосном сжатии значительно больше прочности при простом (одноосном) сжатии. При всестороннем сжатии прочность возрастает еще в большей мере. Твердые породы в условиях всестороннего сжатия не разрушаются даже при очень высоких давлениях, измеряемых многими тысячами атмосфер. В частных случаях наблюдается повышение предела прочности на сжатие на величину, примерно равную прочности всестороннего сжатия.
Прочность пород на сжатие и растяжение, сдвиг характеризуется их пределом прочности, представляющим критическое значение одноосного напряженного состояния, при котором происходит разрушение породы. Прочность горных пород в одноосном напряженном состоянии изменяется в широких пределах: на сжатие от 1∙105 до 4∙108 Па; на растяжение - 0 до 4∙107 Па; на сдвиг - 1∙104до 7∙107 Па.
При всестороннем сжатии прочность пород возрастает в 3-5 раз. Повышается и предел упругости пород.
Прочность пород зависит также от скорости приложения нагрузки. При динамическом (ударном) вдавливании пуансона в породу сопротивление ее в 8-9 раз меньше, чем при статическом нагружении (вдавливанием пуансона измеряют твердость горных пород). При больших скоростях приложения сжимающих нагрузок сопротивление горных пород разрушению в 10-12 раз больше, чем при статических нагрузках (например, при взрыве).
Контрольные вопросы:
1. При каких условиях происходит разрушение породы?
2. Перечислите факторы, от которых зависит величина предела прочности одной и той же горной породы.
3. Прямые методы испытания пород.
4. Косвенные методы испытания пород.
5. Какова взаимосвязь прочности пород и скорости приложения нагрузки?
Модуль 2. Изучение трещиноватости и механических свойств горных пород
Раздел 5. Деформирование и разрушение горных пород. Прочностные, деформационные и реологические свойства горных пород
Тема 6. Механические свойства горных пород и массивов
ЛЕКЦИЯ № 9
План лекции
3. Упругие и пластические свойства пород и массивов.
4. Ползучесть и релаксация.
5. Наследственная теория ползучести.
Реологические свойства горных пород
Реологические свойства горных пород — это свойства, связанные с их деформированием во времени. Для их характеристики пользуются понятиями «ползучесть» и «релаксация».
Ползучесть — способность породы развивать во времени деформации при постоянной нагрузке, а релаксация — способность породы снижать во времени напряжение (расслабляться) при постоянной, наперед заданной деформации.
Характер деформирования горных пород во времени обычно иллюстрируется кривой ползучести (рис.1.), которая в наиболее общем случае включает три характерные стадии деформирования.
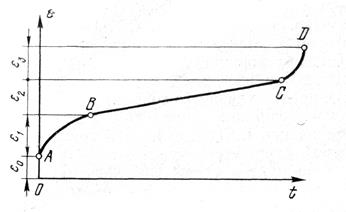
Рис.1. График ползучести горных пород
Участок ОА соответствует начальной условно-мгновенной деформации. В зависимости от величины приложенного напряжения она может быть как упругой, связанной с упругим сжатием минерального скелета, защемленного воздуха и воды, так и частично необратимой, обусловленной микроразрушениями (сдвигом частиц, их переориентацией, частичным нарушением жестких связей).
Участок АВ соответствует стадии неустановившейся или затухающей ползучести. Для ползучести породы в этой стадии также характерны как упругая, так и необратимая деформации.
Участок ВС соответствует стадии установившейся ползучести или ползучести с постоянной скоростью (е = const). Эта стадия формирования характеризуется разрушением структурных связей, и поэтому деформации при разгрузке восстанавливаются лишь частично.
Участок CD характеризуется увеличением скорости деформирования, что связано с интенсификацией процесса разрушения, появлением трещин и, наконец, полным разрушением. Этот участок соответствует стадии прогрессирующего течения.
Рассмотренный случай является наиболее общим для горных пород. Ниже будет показано, что характер деформирования конкретных горных пород может иметь несколько иной характер.
Связь между переменным (напряжением, деформацией, скоростями их изменения и временем), входящими в реологическое уравнение состояния, устанавливается на основании теории ползучести. В механике горных пород наибольшее распространение получили теории упруго-вязко-пластической среды и наследственной ползучести.
В теории упругости предполагается, что все тела обладают свойством упругости. Под упругостью понимают способность восстанавливать свои первоначальные форму и размеры после устранения сил, которые вызывали деформацию. Теория упругости рассматривает идеально упругие тела, т.е. такие, которые полностью восстанавливают свою форму, размеры и взаимное расположение частиц.
Тело всегда имеет форму, зависящую лишь от тех нагрузок, которые действуют на тело в данный момент, и не зависящую от того, какие нагрузки оно испытывало в предыдущие моменты времени. Примером совершенной упругости могут служить кристаллы некоторых твердых минералов (кварца, алмаза). Под действием равномерно распределенных нагрузок они деформируются на очень малые величины, зависящие только от мгновенных значений нагрузки. После разгрузки деформации полностью исчезают. Все выводы теории упругости основываются на законе Гука о прямой пропорциональности между напряжением и деформацией, Большинство горных пород и строительных материалов в известной степени обладают свойствами упругости. Если силы, вызвавшие деформации не превосходят определенной величины, то можно рассматривать материал как упругий. Как показывают многочисленные исследования, для многих прочных пород типа гранита, кварцитов, известняков, а также для некоторых углей прямая пропорциональность между напряжениями и деформациями сохраняется вплоть до момента разрушения.
Линейная теория упругости описывает деформирование тела с помощью линейных уравнений. При этом вводят допущения о малости перемещений, поворотов, деформаций, что позволяет применять недеформированную схему тела с использованием закона Гука.
Например, участок от начала координат до предела пропорцинальности А (рис. 2.) соответствует закону Гука. Связь между напряжением и деформацией остальной части кривой, где наряду с упругой деформацией наблюдается также остаточная деформация, изучается в теории пластичности.
Материал может быть упругим, но не подчиняться закону Гука (рис. 2.7). Нагрузка происходит по кривой ОАВ, а медленная разгрузка - по кривой ВАО, причем в обратном порядке (рис. 2.7)
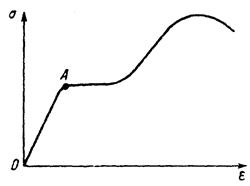
Рис. 2. Диаграмма напряжений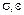 
Теория, исследующая деформации и напряжения в таком теле, называется нелинейной теорией упругости.
Многие строительные материалы и горные породы, например упруго-пластичные материалы, при разгрузке не приходят в исходное положение (рис. 3).
Разгрузка происходит по прямой ВС, отрезок ОС соответствует остаточной деформации.
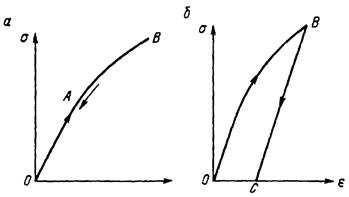
Рис. 3. Диаграммы напряжений 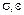при: а – нелинейной упругости; б – уругопластичной деформации.
Как известно основное различи; между хрупкими и пластичными материалами заключается в том, что хрупкие разрушаются при незначительных деформациях, а пластичные - лишь после значительных изменений формы. Пластичность – это способность тела получать под действием нагрузок остаточные деформации. Примером пластичного материала является свинец, который почти не возвращается в первоначальную форму после удаления деформирующих сил.
Почти все твердые вещества в большей или меньшей степени обладают свойством пластичности. При больших давлениях могут течь без разрушения даже такие материалы, которые принято считать хрупкими. Например, горные породы на большой глубине под действием высокого всестороннего давления текут, испытывая большие пластические деформации.
В сопротивлении материалов рассмотрены некоторые задачи, касающиеся определения несущей способности балок и статически неопределимых систем. При этом имеется в виду, что материал по достижении предела текучести приобретает свойства, характерные для идеально пластичного тела (рис. 4, а). Для упрощения теоретических расчетов принимают длину площадки текучести неограниченной. Такое упрощение допустимо в тех случаях, когда площадка текучести имеет большую протяженность, причем заранее известно, что материал при наибольших нагрузках не достигнет состояния упрочнения.
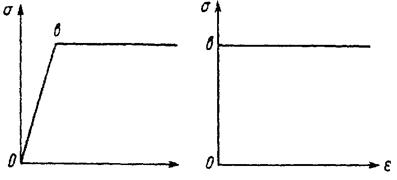
Рис. 4. Диаграммы напряжений 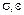материала: а – идеально упругопластичного; б – идеально жёсткопластичного.
В действительности площадка текучести во многих случаях имеет небольшую длину, после которой рост деформации сопровождается ростом напряжений. Во многих материалах, в том числе в горных породах, площадка текучести, как правили не наблюдается.
Иногда для определения несущей способности пренебрегают упругими деформациями и пользуются еще более идеализированной кривой 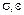(рис. 4, 6). Если упрочнение за пределом упругости незначительно, то кривую зависимости - можно предать в идеализированном виде без упрочнения. При постоянной нагрузке, вызывающей пластическое состояние по всему сечению, тело теряет возможность оказывать возрастающее сопротивление нагрузке и деформация растет.
Деформации называются упруго-пластичными, когда в одних частях тела возникают только упругие, в других только пластические деформации. Деформации считаются малыми, если можно пренебречь их произведениями и квадратами по сравнению с самими деформациями.
В теории пластичности различают активную и пассивную деформации. Активная деформация связана с непрерывным ростом нагрузки, например, при осевом растяжении. При разгрузке деформация считается пассивной.
Если в теле возникают только упругие деформации, то оно ведет себя совершенно одинаково как при нагрузке, так и при разгрузке, следовательно, зависимость между напряжением и деформацией однозначна в обоих случаях.
При напряжениях выше предела упругости в теле возникают пластические деформации и зависимость между напряжениями и деформациями при активной деформации резко отличается от зависимости при пассивной деформации. При активной деформации пластическая деформация возрастает, при пассивной - происходит лишь уменьшение упругой деформации, пластическая деформация не изменяется.
Наряду с упругостью и пластичностью важное значение имеет вязкость. Тело называется вязким, если скорость необратимых деформаций возрастает с ростом напряжений, вызывающих деформацию. Напряжения в состоянии текучести зависят лишь от скорости деформации, но не от самой деформации.
Тело называется вязко-пластичным, если оно соединяет в себе свойства, характеризуемые этими двумя понятиями. Такой материал следует закону деформирования, выражаемому уравнением
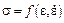
Идеально вязким считается тело, у которого скорость деформации пропорциональна напряжению. Существуют тела, у которых вязкость проявляется наряду с упругостью.
Постоянная скорость деформации реализуется путем растяжения образцов при данной относительной скорости захватов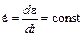 
(рис. 5 а), постоянная скорость нагружения получается путем увеличения в испытуемом образце напряжения на одинаковые величины в одинаковые промежутки времени 
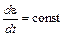(рис. 5 б).
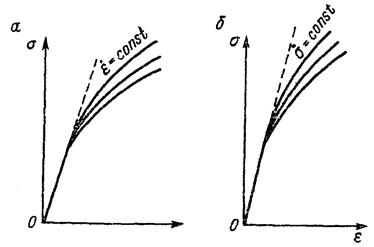
Рис. 5. Диаграммы напряжений 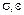при постоянной скорости: а – деформирования; б – нагружения.
Ползучестью называют необратимый рост деформации во времени при неизменных внешних нагрузках. С течением времени скорость ползучести при данном напряжении монотонно убывает, стремясь к некоторому предельному значению.
Состояние установившейся ползучести наступает при деформациях ползучести, заметно преобладающих над упругими деформациями. Задачи установившейся ползучести отличаются известной простотой, поэтому в технике большей частью ограничиваются анализом установившейся ползучести.
Наиболее важна зависимость разрушающего напряжения от времени: разрушение наступает при всяком напряжении, при высоком напряжении оно происходит через сравнительно короткий промежуток времени, при низком - время до момента разрушения оказывается значительным, Вместо предела прочности здесь вводится другая характеристика - длительная прочность, т.е. напряжение, вызывающее разрушение за данный промежуток времени.
Цель теоретического описания процесса ползучести - определить деформации после определенного времени и установить условия разрушения. В отличие от обычных расчетов на прочность, при расчетах на ползучесть ставят задачу не обеспечить абсолютную прочность, а лишь гарантировать, что нормальные условия работы не будут нарушены до ранее определенного срока.
Таким образом, задачей теории является разработка методов определения деформации в телах, подверженных ползучести, и методов определения времени до разрушения.
Релаксацией называется процесс самопроизвольного ослабления напряжений. Явление релаксации объясняется развитием в теле деформаций ползучести, вследствие чего снижается величина упругой деформации. Процесс релаксации можно представить как ползучесть, протекающую при уменьшающемся напряжении.
Релаксация приводит к тому, что концентрация напряжений со временем ослабевает, распределение напряжений становится более равномерным и максимум напряжений снижается. В этом случае влияние релаксации на прочность благоприятно.
Связь теории упругости, ползучести и пластичности с сопротивлением материалов
Теории упругости, пластичности и ползучести следует рассматривать как высшую ступень развития сопротивления материалов, где углубляются теоретические положения о напряженно-деформированном состоянии тела произвольной формы. Получаемые результаты позволяют проверить упрощенные решения, рассматриваемые в сопротивлении материалов.
Объектом изучения в сопротивлении материалов служит действие сил на брус, решаются так называемые одномерные задачи при различных видах деформации: растяжение - сжатие, изгиб, кручение и при различных сочетаниях этих деформаций. Стержень или брус характеризуется тем, что имеет один размер -длину, намного превосходящую другие размеры (высоту и ширину поперечного сечения). Эти задачи рассматриваются также в теориях упругости и пластичности, но более строго, без применения упрощающих предположений и гипотез.
Так, при изучении изгиба в сопротивлении материалов вводится гипотеза плоских сечений: поперечные сечения, бывшие плоскими до деформации, остаются плоскими и после деформации. Гипотеза плоских сечений является точной для чистого изгиба балки, но она несовместима с наличием касательных напряжений, 
(ху), (хz) связанных со сдвигом. Гипотеза приблизительно соответствует действительности, поскольку эти напряжения малы равнению с нормальными напряжениями. Строгое решение задачи методами теории упругости показывает, что гипотеза плоских сечений дает удовлетворительные результаты только в тех случаях, когда размеры сечения балки малы по сравнению с пролетом. Если же высота балки сравнима с ее длиной, то решение, полученное в сопротивлении материалов, уже не верно и следует воспользоваться теорией упругости.
Методами сопротивления материалов нельзя решать задачи определение напряжений и деформаций в телах, имеющих форму пластины или оболочки; задачу о напряженном состоянии массива, имеющую большое значение в горном деле; контактные задачи; определять концентрацию напряжений у отверстия, в местах: резких переходов и многие другие. Все перечисленные задачи могут быть решены только исходя из более общих предпосылок, при помощи методов, обеспечивающих большую строгость решения по сравнению с сопротивлением материалов.
Исторические замечания
Теория упругости сформировалась как самостоятельная дисциплина в первой половине XIX в. Быстрое развитие железных , машиностроения вызвало необходимость создать теоретические методы расчета частей сооружений и машин на прочность. Огромные успехи математики, которая решала задачи, поставленная перед ней физикой, послужили основой создания математической теории упругости, изучающей напряжения и деформации в упругом теле под действием внешних сил.
Наиболее значительный вклад в разработку основ теории ости внесли французские ученые О.Коши, Л.Навье и Б.Сен-Венан, получившие основные дифференциальные уравнения. Большую роль в развитии теории упругости сыграли работы И.И.Остроградского, А.Лямэ, А.Н.Крылова, С.П.Тимошенко, Б.Г.Галеркина и др.
Начиная со второй четверти XX в. исследователи уделяли все больше внимания поведению материала за пределом упругости изучению напряжений и деформаций в пластической зоне, Наиболее важные результаты были получены А.А.Ильюшиным, разработавшем теорию малых упругопластических деформаций, В.В.Соколовским, А.А.Гвоздевым и др. Среди исследований, выполненных в этой области за рубежом, следует выделить работы американского ученого А.Надаи, много сделавшего для развития теории пластичности и ползучести.
Со второй половины XX в. начала интенсивно развиваться теория ползучести. Серьезным толчком для этого послужило изучение явлений ползучести, связанных с высокими температурами в котлах и турбинах. В дальнейшем аналогичные исследования проводились применительно к задачам горного давления, где ползучесть проявляется при обычных температурах и является решающим фактором при определении устойчивости выработок. Здесь выделяются работы Ю.Н.Работнова, Л.М.Качалова, Е.С.Ержанова, М.И.Розовского и др.
Контрольные вопросы:
1. Что понимается под реологическими свойствами горных пород?
2. Дайте определения понятиям ползучести и релаксации.
3. Прямые методы испытания пород.
4. Какие породы обладают пластичностью?
5. Что такое длительная прочность?
Модуль 2. Изучение трещиноватости и механических свойств горных пород
Раздел 5. Деформирование и разрушение горных пород. Прочностные, деформационные и реологические свойства горных пород
Тема 7. Методы определения свойств горных пород
ЛЕКЦИЯ № 10
План лекции
6. Прочностные и деформационные свойства пород.
7. Прямые и косвенные методы определения механических свойств.
Дата: 2019-02-25, просмотров: 378.
