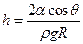 ,
,
где a - коэффициент поверхностного натяжения; q - краевой угол (q = 0 при полном смачивании поверхности жидкостью; q = p при полном несмачивании); r - плотность жидкости; g - ускорение свободного падения; R - радиус канала капиллярной трубки.
Пример 1. В цилиндр длиной l0 = 2 м, заполненный воздухом при нормальном давлении р =1×105 Па, начали медленно вдвигать поршень площадью S = 100 см2. Определить давление p1 в цилиндре и силу F, которая будет действовать на поршень, если поршень остановится на расстоянии l1 = 2 см от дна цилиндра. (Вес поршня не учитывать).
| Дано: l0 =2 м р0 = 1×105 Па S = 100 см2 l1 = 2 см | В единицах СИ: S = 1×10-2 м2 l1 = 2 ×10-2 м | Решение. 1. Если поршень вдвигать медленно, воздух практически не нагревается, и процесс можно считать изотермическим (T = const). Уравнение такого процесса имеет вид: p0V0 = p1V1, где р0 = 105 Па – начальное давление, V0 = l0×S – начальный объем газа, р1 – конечное давление, а V1 = l1× S – конечный объем газа. Из этого уравнения следует, что: |
| Найти: р1, F |
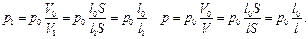 (28)
(28)
2. Силу, действующую на поршень, найдем из выражения для давления:
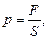 откуда
откуда 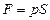 .
.
Произведем вычисления:
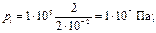
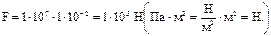
Ответ. 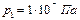 ; F = 1×105 Н.
; F = 1×105 Н.
Пример 2. Под каким давлением находится кислород ( 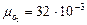 кг/моль) в баллоне объемом V = 10 л и чему равна суммарная кинетическая энергия всех его молекул при условии, что концентрация и средняя квадратичная скорость молекул кислорода составляют, соответственно,
кг/моль) в баллоне объемом V = 10 л и чему равна суммарная кинетическая энергия всех его молекул при условии, что концентрация и средняя квадратичная скорость молекул кислорода составляют, соответственно, 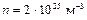 и
и 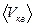 = 103 м/с.
= 103 м/с.
|
Дано:
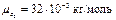 V = 10 л
п = 2×1025 м-3
V = 10 л
п = 2×1025 м-3
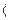 vквñ = 103 м/с
NА = 6,02 · 1023 моль-1
R = 8,31 Дж/(моль×К) vквñ = 103 м/с
NА = 6,02 · 1023 моль-1
R = 8,31 Дж/(моль×К)
| В единицах СИ: V = 1×10-2 м3 | Решение. 1. Для нахождения давления газа p воспользуемся уравнением Клапейрона–Менделеева
Массу газа можно выразить через известные величины следующим образом: |
| Найти: p, Е. |
m = N×m0где N = n×V число молекул газа; n - концентрация газа; V - объем газ; 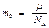 - масса одной молекулы кислорода, m - молярная масса газа; NA - число Авогадро.
- масса одной молекулы кислорода, m - молярная масса газа; NA - число Авогадро.
Таким образом:
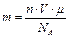 ,
, 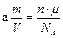 . (30)
. (30)
Температуру газа можно определить исходя из выражения для средней квадратичной скорости молекул 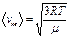 .
.
Находим:
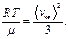 (31)
(31)
Подставляя полученные выражения (30) и (31) в (29), окончательно получим:
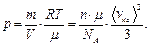 (32)
(32)
2. Суммарная кинетическая энергия всех молекул газа есть ни что иное, как внутренняя энергия газа
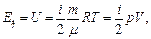 (33)
(33)
где i = 5 – число степеней свободы для двухатомных молекул газа.
Подставив в (33) полученное выше выражение (32) для давления p, получим
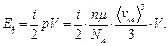 (34)
(34)
Произведем вычисления по формулам (4) и (6):
 ;
;
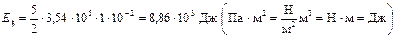 .
.
Ответ. Газ находится по давлением p = 3,54×105 Па, а его суммарная кинетическая энергия составляет Eк = 8,86×103 Дж.
Пример 3. Двухатомный газ под давлением р = 150 кПа и при температуре t ° = 27°С занимает объем V = 100 л. Определить теплоемкость этого газа при постоянном объеме сV и при постоянном давлении ср.
| Дано: i = 5 р = 150 кПа t° = 27°С V = 100 л | В единицах СИ р = 1,5 · 105 Па Т =300 К V = 0,1 м3 | Решение. Теплоемкости произвольной массы газа m при постоянном объеме сV и при постоянном давлении ср могут быть выражены через молярные теплоемкости, соответственно, при постоянном объеме |
| Найти: cV, ср |
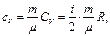 (35)
(35)

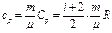 , (36)
, (36)
где m - масса газа, μ – молярная масса газа, i = 5 – число степеней свободы для молекул двухатомного газа, R = 8,31 Дж/(моль×К) - универсальная газовая постоянная.
Из уравнения Клапейрона-Менделеева
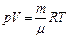 (37)
(37)
|
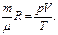 Следовательно, уравнения (35) и (36) принимают вид:
Следовательно, уравнения (35) и (36) принимают вид:
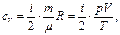 (38)
(38)

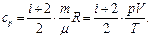 (39)
(39)
Произведем вычисления по формулам (38) и (39):
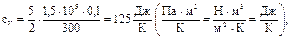
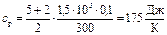
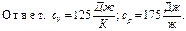

 Пример 4. В цилиндре объемом V = 6 л под поршнем, занимающим среднее положение (рис. 2.1), находится водород Н2 при атмосферном давлении (р0 = 105 Па). При нагревании газ расширяется при постоянном давлении, в результате чего поршень поднимается вверх до упора, после чего давление газа постепенно возрастает в два раза. Построить pV- и VT-диаграммы наблюдаемых изопроцессов и определить теплоту Q , переданную газу. Трением поршня о стенки сосуда, а также весом поршня и его толщиной пренебречь.
Пример 4. В цилиндре объемом V = 6 л под поршнем, занимающим среднее положение (рис. 2.1), находится водород Н2 при атмосферном давлении (р0 = 105 Па). При нагревании газ расширяется при постоянном давлении, в результате чего поршень поднимается вверх до упора, после чего давление газа постепенно возрастает в два раза. Построить pV- и VT-диаграммы наблюдаемых изопроцессов и определить теплоту Q , переданную газу. Трением поршня о стенки сосуда, а также весом поршня и его толщиной пренебречь.
| Дано: V1 = 3 л V2 = V = 6 л p1 = р0 = 1×105 Па m = 2×103 кг/моль р2 = 2р1 | В единицах СИ: V1 = 6×10-3 м3 V2 = 3×10-3 м3 | Решение. На первом этапе газ расширяется от V1 до V2 при постоянном давлении р0, т. е. протекает изобарический процесс, а затем газ нагревается при постоянном объеме, то есть идет изохорический процесс. Представим эти процессы на pV-диаграмме и VT-диаграмме.
|
| Найти: Q |
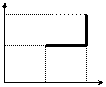
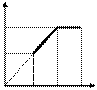
1. На pV-диаграмме (рис.2.2) показано, что переход из состояния 1 в состояние 2 происходит при постоянном давлении р0 (изобарический процесс), а переход из состояния 2 в состояние 3 – при постоянном объеме V2 (изохорический процесс). На VT-диаграмме (рис. 2.3) эти же переходы представлены зависимостями V/ T = const (1®2) и V = const (2®3). T1, T2 и T3 - температуры газа в состояниях 1, 2 и 3, соответственно.
2. Суммарное количество теплоты, Qp переданное газу, найдем как сумму количеств теплоты, переданных при изобарическом и изохорическом QV процессах.
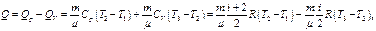 (40)
(40)
где i = 5 – число степеней свободы для двухатомной молекулы Н2; т – масса газа; μ - молярная масса водорода Н2; R = 8,31 Дж/(моль×К)– газовая постоянная.
 p
p1 3
p0 1 2
V1 V2 V p
p1 3
p0 1 2
V1 V2 V
|  V
2 3
V2
1
V1
T1 T2 T3 T V
2 3
V2
1
V1
T1 T2 T3 T
|
| Рис. 2.2 | Рис. 2.3 |
Воспользовавшись уравнением Клапейрона-Менделеева 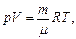 полученное выражение (40) для Q можно представить в виде:
полученное выражение (40) для Q можно представить в виде:
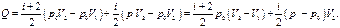 (41)
(41)
Произведем вычисления по формуле (41):
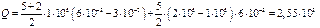 Дж
Дж
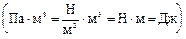
Ответ. Суммарное количество теплоты, переданное газу, Q = 2,55 кДж.
Пример 5. Трехатомный (i = 6) газ совершает цикл Карно (см. рис. 2.4). Объем газа в точке В составляет 6 м3. Определить объем газа в точке С, если КПД цикла равен 22%.
Дано:
i=6
V В = 6 м3
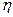 = 22% = 22%
| в единицах СИ
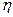 = 0,22 = 0,22
|
B
D C V
|
| Найти: VС |
|
Решение: Так как переход из точки В в точку С газ совершает адиабатически, то воспользуемся уравнением для этого процесса (уравнение Пуассона) в виде:
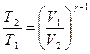 , (1)
, (1)
где Т1 – температура газа в точке В, Т2 – температура
газа в точке С, V1 = VВ – объем газа в точке В,
V2 = VС – объем газа в точке С, 
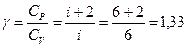 - показатель адиабаты.
- показатель адиабаты.
Так как 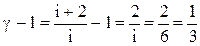 для трехатомного газа, представим уравнение (1) в виде:
для трехатомного газа, представим уравнение (1) в виде:
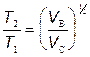 Þ
Þ 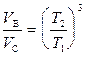 (2)
(2)
Отношение 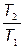 находим из формулы для КПД цикла Карно:
находим из формулы для КПД цикла Карно:
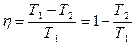 Þ
Þ 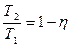 . (3)
. (3)
Подставляя полученное выражение (3) в (2), окончательно находим:
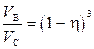 Þ
Þ 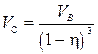 (4)
(4)
Произведем вычисления по формуле (4):
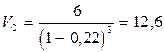 м3
м3
Ответ: Объем газа в точке С составляет 12,6 м3.
Пример 6. Найти изменение энтропии при охлаждении азота массой m = 10 г от 80 0С до 0 0С
а) при постоянном объеме
б) при постоянном давлении.
Дано:
N2
m = 28×10-3 кг/моль
m = 10 г
 = 80 0С = 80 0С
 = 0 0С
R =8,31 Дж/(моль×К)
а) V = const
б) p = const = 0 0С
R =8,31 Дж/(моль×К)
а) V = const
б) p = const
| в единицах СИ m = 1×10-2 кг Т1 = 353 К Т2 = 273 К | Решение: Изменение энтропии будем искать по формуле: где dQ – малое изменение теплоты при температуре Т. При изохорном процессе
|
Найти: 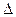 S V ,, S V ,, 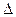 Sp Sp
|
При изобарном процессе
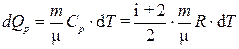 (3)
(3)
Подставляя полученные соотношения (2) и (3) в выражение (1) для изменения энтропии, получим:
а) для изохорного процесса

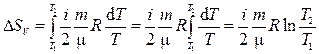 (4)
(4)
б) для изобарного процесса
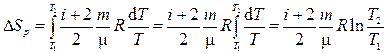 (5)
(5)
Произведем вычисления по формулам (4) и (5):
|
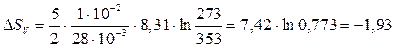 Дж/К,
Дж/К,
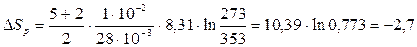 Дж/К.
Дж/К.
Знак (-) означает, что энтропия газа при уменьшении его температуры уменьшилась.
Ответ: Энтропия газа уменьшится при уменьшении температуры на 1,93 Дж/К при изохорном процессе и на 2,7 Дж/К при изобарном процессе.
Пример 7. Наружная поверхность неоштукатуренной кирпичной стены толщиной 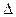 х =50 см (два кирпича) имеет температуру -10 0С, внутренняя +20 0С. За сутки через 1 м2 стены за счет теплопроводности теряется количество тепла Q = 3,6
х =50 см (два кирпича) имеет температуру -10 0С, внутренняя +20 0С. За сутки через 1 м2 стены за счет теплопроводности теряется количество тепла Q = 3,6 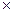 106 Дж. Определить коэффициент теплопроводности кирпичной кладки.
106 Дж. Определить коэффициент теплопроводности кирпичной кладки.
Дано:
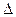 х = 50 см х = 50 см
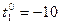 оС. оС.
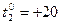 оС.
S = 1 м2
t = 24 ч
Q = 3,6 оС.
S = 1 м2
t = 24 ч
Q = 3,6  106 Дж 106 Дж
| в единицах
СИ
 х = 0,5 м
Т1 = 263 К
Т2 = 293 К
t = 8,64×104 с х = 0,5 м
Т1 = 263 К
Т2 = 293 К
t = 8,64×104 с
| Решение: Считая стену бесконечной, температуры Т1 и Т2 постоянными, процесс теплопроводности установившимся, уравнение теплопроводности можно записать в виде: Q = æ× где Q – количество теплоты прошедшей через стену толщиной через площадь S за время t , æ – коэффициент теплопроводности.
| |
| Найти: æ | |||
Из уравнения (1) находим коэффициент теплопроводности:
æ = 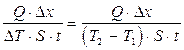
Произведем вычисления:
æ = 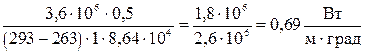
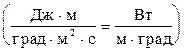 .
.
Ответ: Коэффициент теплопроводности æ = 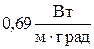 .
.
Пример 8. Горизонтально расположенный капилляр с внутренним радиусом
R =1мм и длиной l = 10 см полностью заполнен водой. Когда капилляр поставили вертикально, опустив нижний конец в воду на пренебрежимо малую глубину, часть воды вытекла. Определить массу вытекшей воды. Плотность воды 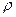 = 1×103 кг/м3, коэффициент поверхностного натяжения
= 1×103 кг/м3, коэффициент поверхностного натяжения 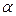 = 72
= 72 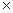 10-3 Н/м.
10-3 Н/м.
Дано:
R = 1 мм
l = 10 см
r = 1×103 кг/м3
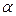 = 72 = 72 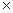 10-3 Н/м 10-3 Н/м
| в единицах СИ R = 1×10-3 м l = 1×10-1 м | Решение: Масса воды, полностью заполняющей капилляр, равна 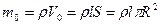 ,
где r - плотность воды,
l – длина капилляра,
R – радиус капилляра.
Когда капилляр поставлен вертикально, причем нижний конец находится в воде, высота уровня воды будет ,
где r - плотность воды,
l – длина капилляра,
R – радиус капилляра.
Когда капилляр поставлен вертикально, причем нижний конец находится в воде, высота уровня воды будет
|
Найти: 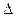 т т
|  , (1) , (1)
|
где 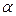 - коэффициент поверхностного натяжения,
- коэффициент поверхностного натяжения,
q = 0 - краевой угол при полном смачивании - плотность воды,
g = 9,8 м/с2 - ускорение свободного падения.
Тогда масса воды, оставшейся в капилляре, будет равна:
m = rV = rhS = 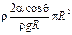 , или, так как cosq = 1, m =
, или, так как cosq = 1, m = 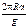 (2)
(2)
Следовательно,
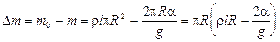 (3)
(3)
|
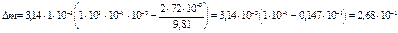 кг.
кг.
Ответ: Масса вытекшей из капилляра воды равна 0,268 г.
Варианты задач
Дата: 2019-02-25, просмотров: 309.
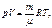 из которого следует
из которого следует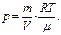 . (29)
. (29)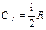 и при постоянном давлении
и при постоянном давлении 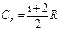 следующим образом:
следующим образом: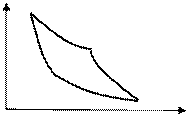 p A
p A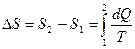 , (1)
, (1) (2)
(2)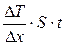 , (1)
, (1)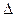 х при разности температур
х при разности температур