Раздел 2.
ТЕРМОДИНАМИКА
И МОЛЕКУЛЯРНАЯ ФИЗИКА
Основные формулы
Количество вещества тела (системы)
n = N/NA = m/ m ,
где N - число структурных элементов (атомов; молекул, ионов и т. п.), составляющих тело (систему); NA - число Авогадро; m - масса тела (вещества); m - молярная масса вещества.
Основное уравнение молекулярно-кинетической теории газов
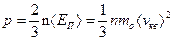
или p = nkT,
где 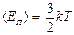 - средняя кинетическая энергия поступательного движения молекулы; n = N/V - концентрация молекул; k - постоянная Больцмана.
- средняя кинетическая энергия поступательного движения молекулы; n = N/V - концентрация молекул; k - постоянная Больцмана.
Уравнение Клапейрона-Менделеева (уравнение состояния идеального газа)
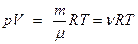 ,
,
где m - масса газа; V - объем газа; R - молярная газовая постоянная; Т - термодинамическая температура.
Средняя полная кинетическая энергия молекулы
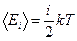 ,
,
где i - число степеней свободы молекулы.
Скорости молекул:
– средняя квадратичная
|
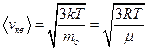 ;
;
– средняя арифметическая
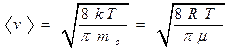 ;
;
– наиболее вероятная
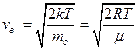 =
= 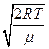 .
.
где mo - масса одной молекулы.
Молярная теплоемкость газа:
– при постоянном объеме
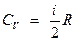 ;
;
– при постоянном давлении
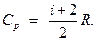
Удельная теплоемкость газа:
– при постоянном объеме
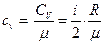 ;
;
– при постоянном давлении
сp = 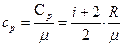 .
.
Внутренняя энергия идеального газа
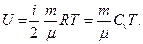
Первое начало термодинамики
Q = DU + A,
|
Работа расширения газа:
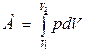 ,
,
– при изобарическом процессе
A = p(V2 - V1);
– при изотермическом процессе
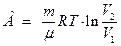 ;
;
– при адиабатном процессе
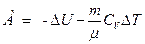
или 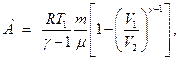
где 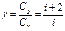 - показатель адиабаты.
- показатель адиабаты.
Уравнения Пуассона, связывающие параметры идеального газа при адиабатном процессе
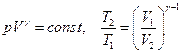 ,
,
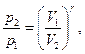
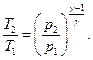
Термический КПД кругового цикла
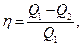
где Q1 - теплота, полученная рабочим телом от теплоотдатчика; Q2 - теплота, переданная рабочим телом теплоприемнику.
Термический КПД цикла Карно
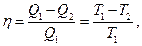
где T1 - термодинамическая температура теплоотдатчика; T2 - термодинамическая температура теплоприемника.
Изменение энтропии при переходе из состояния 1 в состояние 2
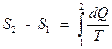 .
.
Средняя длина свободного пробега молекулы
<l> = ( 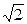 pd2n)-1,
pd2n)-1,
где d - эффективный диаметр молекулы; n - число молекул в единице объема.
Среднее число столкновений молекулы в единицу времени
< z > = 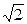 pd2n<v>.
pd2n<v>.
Уравнение диффузии (в направлении x)
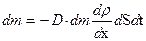 ,
,
где D - коэффициент диффузии; r - плотность; dS - элементарная площадка, перпендикулярная оси Оx.
Уравнение теплопроводности
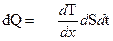 ,
,
|
Коэффициент диффузии
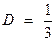 <v><l>.
<v><l>.
Динамическая вязкость
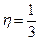 r<v><l> = Dr.
r<v><l> = Dr.
Теплопроводность
æ = 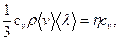
где cv - удельная теплоемкость газа при постоянном объеме.
Рис.2.4
|
Решение: Так как переход из точки В в точку С газ совершает адиабатически, то воспользуемся уравнением для этого процесса (уравнение Пуассона) в виде:
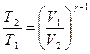 , (1)
, (1)
где Т1 – температура газа в точке В, Т2 – температура
газа в точке С, V1 = VВ – объем газа в точке В,
V2 = VС – объем газа в точке С, 
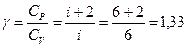 - показатель адиабаты.
- показатель адиабаты.
Так как 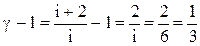 для трехатомного газа, представим уравнение (1) в виде:
для трехатомного газа, представим уравнение (1) в виде:
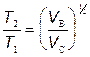 Þ
Þ 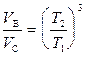 (2)
(2)
Отношение 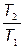 находим из формулы для КПД цикла Карно:
находим из формулы для КПД цикла Карно:
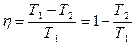 Þ
Þ 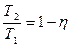 . (3)
. (3)
Подставляя полученное выражение (3) в (2), окончательно находим:
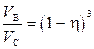 Þ
Þ 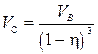 (4)
(4)
Произведем вычисления по формуле (4):
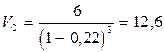 м3
м3
Ответ: Объем газа в точке С составляет 12,6 м3.
Пример 6. Найти изменение энтропии при охлаждении азота массой m = 10 г от 80 0С до 0 0С
а) при постоянном объеме
б) при постоянном давлении.
Дано:
N2
m = 28×10-3 кг/моль
m = 10 г
 = 80 0С = 80 0С
 = 0 0С
R =8,31 Дж/(моль×К)
а) V = const
б) p = const = 0 0С
R =8,31 Дж/(моль×К)
а) V = const
б) p = const
| в единицах СИ m = 1×10-2 кг Т1 = 353 К Т2 = 273 К | Решение: Изменение энтропии будем искать по формуле: где dQ – малое изменение теплоты при температуре Т. При изохорном процессе
|
Найти: 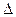 S V ,, S V ,, 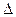 Sp Sp
|
При изобарном процессе
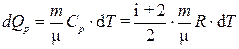 (3)
(3)
Подставляя полученные соотношения (2) и (3) в выражение (1) для изменения энтропии, получим:
а) для изохорного процесса

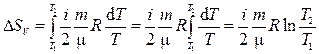 (4)
(4)
б) для изобарного процесса
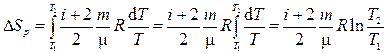 (5)
(5)
Произведем вычисления по формулам (4) и (5):
|
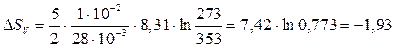 Дж/К,
Дж/К,
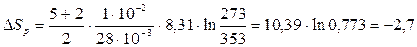 Дж/К.
Дж/К.
Знак (-) означает, что энтропия газа при уменьшении его температуры уменьшилась.
Ответ: Энтропия газа уменьшится при уменьшении температуры на 1,93 Дж/К при изохорном процессе и на 2,7 Дж/К при изобарном процессе.
Пример 7. Наружная поверхность неоштукатуренной кирпичной стены толщиной 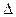 х =50 см (два кирпича) имеет температуру -10 0С, внутренняя +20 0С. За сутки через 1 м2 стены за счет теплопроводности теряется количество тепла Q = 3,6
х =50 см (два кирпича) имеет температуру -10 0С, внутренняя +20 0С. За сутки через 1 м2 стены за счет теплопроводности теряется количество тепла Q = 3,6 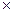 106 Дж. Определить коэффициент теплопроводности кирпичной кладки.
106 Дж. Определить коэффициент теплопроводности кирпичной кладки.
Дано:
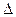 х = 50 см х = 50 см
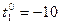 оС. оС.
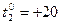 оС.
S = 1 м2
t = 24 ч
Q = 3,6 оС.
S = 1 м2
t = 24 ч
Q = 3,6 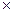 106 Дж 106 Дж
| в единицах
СИ
 х = 0,5 м
Т1 = 263 К
Т2 = 293 К
t = 8,64×104 с х = 0,5 м
Т1 = 263 К
Т2 = 293 К
t = 8,64×104 с
| Решение: Считая стену бесконечной, температуры Т1 и Т2 постоянными, процесс теплопроводности установившимся, уравнение теплопроводности можно записать в виде: Q = æ× где Q – количество теплоты прошедшей через стену толщиной через площадь S за время t , æ – коэффициент теплопроводности.
| |
| Найти: æ | |||
Из уравнения (1) находим коэффициент теплопроводности:
æ = 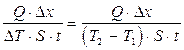
Произведем вычисления:
æ = 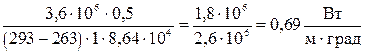
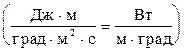 .
.
Ответ: Коэффициент теплопроводности æ = 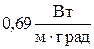 .
.
Пример 8. Горизонтально расположенный капилляр с внутренним радиусом
R =1мм и длиной l = 10 см полностью заполнен водой. Когда капилляр поставили вертикально, опустив нижний конец в воду на пренебрежимо малую глубину, часть воды вытекла. Определить массу вытекшей воды. Плотность воды 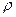 = 1×103 кг/м3, коэффициент поверхностного натяжения
= 1×103 кг/м3, коэффициент поверхностного натяжения 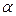 = 72
= 72 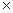 10-3 Н/м.
10-3 Н/м.
Дано:
R = 1 мм
l = 10 см
r = 1×103 кг/м3
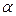 = 72 = 72  10-3 Н/м 10-3 Н/м
| в единицах СИ R = 1×10-3 м l = 1×10-1 м | Решение: Масса воды, полностью заполняющей капилляр, равна 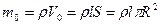 ,
где r - плотность воды,
l – длина капилляра,
R – радиус капилляра.
Когда капилляр поставлен вертикально, причем нижний конец находится в воде, высота уровня воды будет ,
где r - плотность воды,
l – длина капилляра,
R – радиус капилляра.
Когда капилляр поставлен вертикально, причем нижний конец находится в воде, высота уровня воды будет
|
Найти: 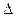 т т
|  , (1) , (1)
|
где 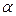 - коэффициент поверхностного натяжения,
- коэффициент поверхностного натяжения,
q = 0 - краевой угол при полном смачивании - плотность воды,
g = 9,8 м/с2 - ускорение свободного падения.
Тогда масса воды, оставшейся в капилляре, будет равна:
m = rV = rhS = 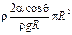 , или, так как cosq = 1, m =
, или, так как cosq = 1, m = 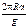 (2)
(2)
Следовательно,
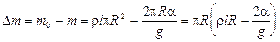 (3)
(3)
|
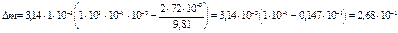 кг.
кг.
Ответ: Масса вытекшей из капилляра воды равна 0,268 г.
Варианты задач
Раздел 3. Теплоемкость газа
221. Вычислить удельные теплоемкости cp и cv газов: 1) гелия He; 2) водорода H2; 3) углекислого газа CO2.
222. Разность удельных теплоемкостей cp - cv некоторого двухатомного газа равна 260 Дж/(кг×К). Найти молярную массу газа и его удельные теплоемкости cp и cv.
223. Двухатомный газ под давлением 300 кПа и при температуре t = 27oС занимает объем V = 50 л. Определить теплоемкость этого газа при постоянном объеме и постоянном давлении.
224. Найти показатель адиабаты g идеального газа, который при температуре Т = 350 К и давлении p = 0,4 МПа занимает объем V = 300 л и имеет молярную теплоемкость Cv = 857 Дж/(моль×К).
225. Трехатомный газ при нормальных условиях (p = 100 кПа, t = 27oС) занимает объем 20 л. Вычислить теплоемкость этого газа при постоянном объеме и постоянном давлении.
226. Плотность некоторого газа при нормальных условиях r = 1,25 кг/м3. Отношение удельных теплоемкостей g = 1,4. Определить удельные теплоемкости cp и cv этого газа.
227. Найти для кислорода отношение удельной теплоемкости при постоянном давлении к удельной теплоемкости при постоянном объеме.
228. Для некоторого двухатомного газа удельная теплоемкость при постоянном давлении cp = 1,46×104 Дж/(кг×К). Чему равна масса одного киломоля этого газа?
229. Чему равны удельные теплоемкости cp и cv некоторого двухатомного газа, если плотность этого газа при нормальных условиях равна 1,43 кг/м3?
230. Найти удельные теплоемкости cp и cv некоторого газа, если известно, что масса одного киломоля этого газа равна m = 30 кг/кмоль и отношение cp/cv =1,4.
Раздел 6. Энтропия
251. Водород массой 2 г изохорически нагрет, в результате чего давление увеличилось в 2 раза. Определить изменение энтропии газа.
252. Азот массой 4 г занимает объем 5 м3. При изобарическом расширении его объем увеличился до 9 м3. Определить изменение энтропии газа.
253. В результате изотермического расширения 10 л газа при температуре 300К его объем достиг 27 л. Давление газа в начале процесса 0,1 МПа. Определить изменение энтропии газа.
254. До какой температуры нужно довести 4 кг кислорода, находящегося при температуре 500 К, не меняя его объема, чтобы уменьшить энтропию газа на 1,31 кДж/К ?
255. При нагревании 8 г аргона его абсолютная температура увеличилась в 2 раза. Определить изменение энтропии при изохорическом и изобарическом нагревании газа.
256. При изобарическом расширении 1 кмоля гелия его объем увеличился в 4 раза. Найти изменение энтропии при этом расширении.
257. Найти изменение энтропии при охлаждении азота массой 2 г от 40 oС до 0 0С: а) при постоянном объеме; б) при постоянном давлении.
258. Масса азота 6 г при давлении 0,1 МПа имела объем 5 л, а при давлении 0,3 МПа – объем 2 л. Переход от первого состояния ко второму был проведен в два этапа: сначала изохорически, затем изобарически. Определить изменение энтропии газа.
259. Определить изменение энтропии газа, используя данные предыдущей задачи 268, если переход от первого состояния ко второму происходит сначала изобарически, а затем изохорически.
260. При изохорическом нагревании некоторой массы двухатомного газа приращение энтропии составило 200 Дж/К. Чему будет равно приращение энтропии при изобарическом нагревании той же массы газа в том же диапазоне температур?
Раздел 7. Явления переноса
Раздел 2.
ТЕРМОДИНАМИКА
И МОЛЕКУЛЯРНАЯ ФИЗИКА
Основные формулы
Количество вещества тела (системы)
n = N/NA = m/ m ,
где N - число структурных элементов (атомов; молекул, ионов и т. п.), составляющих тело (систему); NA - число Авогадро; m - масса тела (вещества); m - молярная масса вещества.
Основное уравнение молекулярно-кинетической теории газов
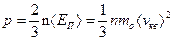
или p = nkT,
где 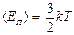 - средняя кинетическая энергия поступательного движения молекулы; n = N/V - концентрация молекул; k - постоянная Больцмана.
- средняя кинетическая энергия поступательного движения молекулы; n = N/V - концентрация молекул; k - постоянная Больцмана.
Уравнение Клапейрона-Менделеева (уравнение состояния идеального газа)
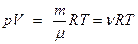 ,
,
где m - масса газа; V - объем газа; R - молярная газовая постоянная; Т - термодинамическая температура.
Дата: 2019-02-25, просмотров: 298.
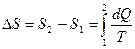 , (1)
, (1) (2)
(2)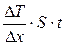 , (1)
, (1)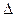 х при разности температур
х при разности температур