Выделите диапазон А2:Е6 и вызовите Мастер диаграмм. Постройте гистограмму, посмотрите, как можно с помощью контекстного меню изменять параметры диаграммы.
Затем выделите несмежные диапазоны В2:В6 и D2:D6 (включая заголовки) и постройте круговую диаграмму. В контекстном меню выберите Параметры диаграммы, перейдите на вкладку Подписи данных и укажите Доля.
Теперь используем мастер диаграмм для построения графиков функций.
Пример: Построим график функции у=sin(х) на отрезке [-2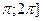 
с шагом h= 
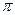/5. Это число получено так: отрезок разбит на n=20 (можно любое) равных частей. Всего будет n+1 узлов разбиения.
1. В ячейку А1 введите: -2*ПИ().
2. В ячейку В1 введите: =SIN(А1).
3. В ячейку А2 введите: =А1+ПИ()/5.
4. Сделайте автозаполнение из В1 в В2.
5. Выделите диапазон А2:В2 и сделайте автозаполнение до 21-й строки.
6. Вызовите Мастер диаграмм. Выберите График, левый верхний образец, далее.
7. На вкладке Диапазон данных проведите мышью по диапазону В1:В21, перейдите на вкладку Ряд. Проведите по диапазону А1:А21, нажмите Готово.
8. Вызовите контекстное меню щелчком по линии графика, опция Формат рядов данных, вкладка Вид. Поставьте флажок Сглаженная линия.
Задание: Построить график функции 
на отрезке [ a ; b ] c шагом h .
Варианты заданий выбираются из. Номер варианта выбирается по сумме последних трёх цифр номера зачётной книжки. Например, зачётная книжка № 931417 ® Вариант № 4+1+7=12 .
| № | n | m | H |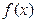 
|
| 0 | – 2 | 2 | 0,25 |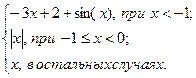 
|
| 1 | – 0.9 | 0.9 | 0,1 |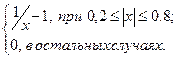 
|
| 2 | – 1 | 3 | 0,2 |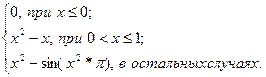 
|
| 3 | 2 | 4 | 0,2 |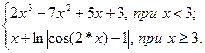 
|
| 4 |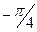 
| 
| 
| 
|
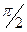
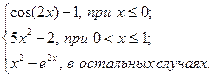
| 5 | – 4 | 0 | 0.4 | 
|
| 6 |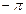 
| 
| 
| 
|
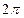
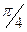
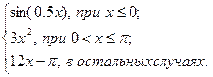
| 7 | 4.2 | 5.85 | 0.15 |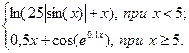 
|
| 8 | – 3 | 6 | 0,5 |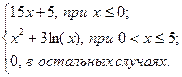 
|
| 9 |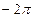 
| 0 | 
| 
|
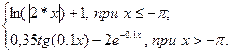
| 10 | – 2.1 | 3 | 0,3 |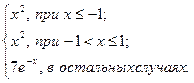 
|
| 11 |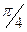 
| 
| 
| 
|
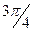
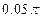
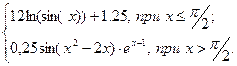
| 12 | – 20 | 20 | 4 |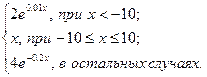 
|
| 13 | 12 | 13.2 | 0.1 |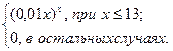 
|
| 14 |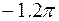 
| 
| 
| 
|
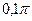
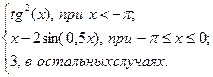
| 15 | – 0.1 | 0.1 | 0,04 |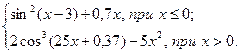 
|
| 16 | 0 | 1,4 | 0,1 |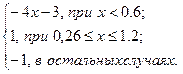 
|
| 17 | – 5 | 5 | 1,5 |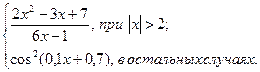 
|
| 18 | – 2 | 2 | 0,25 |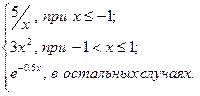 
|
| 19 | – 1.4 | 1.4 | 0,2 |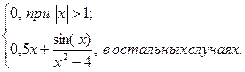 
|
| 20 |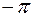 
| 
| 
| 
|
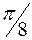
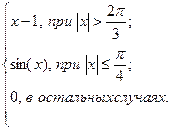
| 21 | – 1,05 | 1,05 | 0,15 |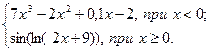 
|
| 22 | 0 | 2,4 | 0,15 |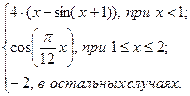 
|
| 23 | – 12 | 0 | 1 | 
|
| 24 | 3 | 7 | 0,25 |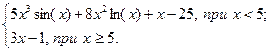 
|
| 25 |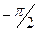 
|
|
| 
|
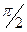
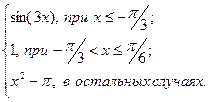
| 26 | 1 | 3 | 0,25 | 
|
| 27 |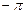 
| 
| 
| 
|
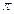
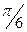
Задание 6. Операции с матрицами.
Рассмотрим систему n линейных алгебраических уравнений с n неизвестными.
Система из n уравнений с n неизвестными, определитель которой не равен 0, обладает решением, притом только одним.
1). Решение можно получить по формулам Крамера:
,
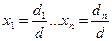где d - определитель системы,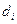 
- определитель, получающийся заменой i-го столбца матрицы системы столбцом 
.
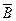Пример. Решить систему:
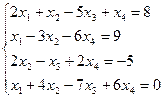
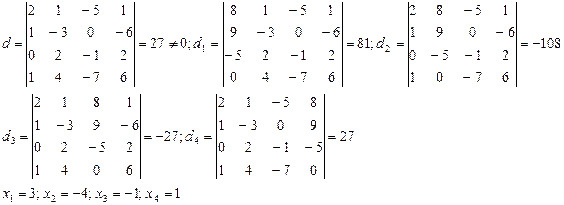
Для нахождения решения пользуемся функцией МОПРЕД.
2). Можно решить систему, исходя из матричного уравнения АХ=В, откуда (А-1А)Х=А-1В, Х=А-1В.
Для обращения матрицы:
1. Ввести элементы матрицы n´n в свободные ячейки (диапазон Х).
2. В свободную ячейку - МОБР(Х).
3. Enter - появится элемент А11-1.
4. Выделить диапазон n´n с А11-1 в качестве левой верхней ячейки.
5. Нажать клавишу F2.
6. Нажать Ctrl+Shift+Enter.
Для умножения матрицы на столбец подготавливаем столбец вместо матрицы и используем МУМНОЖ. Получим Х=А-1В.
Затем делаем проверку: АХ=В должно иметь место.
Задание: Найти решение системы 4 линейных алгебраических уравнений с 4 неизвестными.
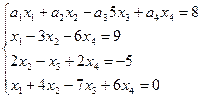
Элементы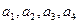 
выбираются по последним четырем цифрам номера зачетной книжки, остальные элементы оставить без изменения. Например, если номер зачетной книжки 060899, система уравнений примет следующий вид:
Задание 7. Подбор параметра.
Рассмотрим подбор параметра при решении уравнений.
Пример: Найти все корни уравнения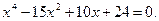 
Введите в ячейку В1 формулу: =A1^4-15*A1^2+10*A1+24. Нажмите Сервис ® Подбор параметра:
Установить в ячейке $В$1
Значение 0
Изменяя значение ячейки $A$1
Результат будет зависеть от того, что записано в А1. Подобранный корень - какой-то из концов отрезка между двумя нулями, содержащего число, записанное в А1.
Получив в А1 число а, делим многочлен столбиком на (х-а). Затем делаем то же самое для нового корня. Все корни: -4, -1, 2, 3.
Задание: Найти все корни уравнения. Варианты заданий выбираются из табл. Номер варианта выбирается по модулю разности последней и четвертой цифры номера зачётной книжки. Например, зачётная книжка № 931423 ®3-4=-1,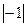 
=1 Вариант № 1.
| № | 
| 
| 
|
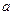
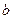
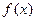
| 0 | – 5,5 | – 4 |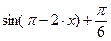 
|
| 1 | 0 | 1 |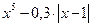 
|
| 2 | 5 | 10 |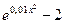 
|
| 3 | 1 | 3 | 
|
| 4 | 1 | 6 |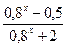 
|
| 5 | – 3 | 1 |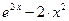 
|
| 6 | 0 | 3 |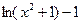 
|
| 7 | 0,2 | 1,4 |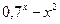 
|
| 8 | 0 | 2 | 
|
| 9 | – 3 | 0 |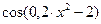 
|
| 10 | 7 | 11 |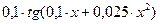 
|
Задание 8. Построение трехмерных диаграмм и графиков
Задание: Построить таблицу значений функции z ( x , y ) и ее отображение в виде поверхности на области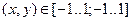 
с шагом 0,1 по каждому направлению. Номер варианта выбирается по разности между последней и предпоследней цифрой шифра из следующей таблицы:
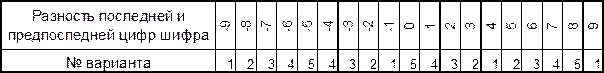
Варианты заданий:
| N вар. | Функция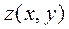 
|
| 1 |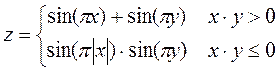 
|
| 2 |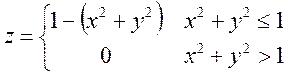 
|
| 3 | 
|
| 4 |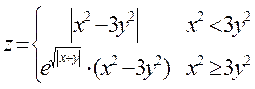 
|
| 5 |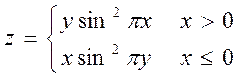 
|
При построении диаграммы – поверхности:
1. поставить подписи оси x и оси y;
2. проградуировать ось z так, чтобы поверхность разбивалась на 5-7 частей; все части окрасить в серый цвет; убрать цвета стенок и основания;
3. выделить оси и установить соответствующие форматы и выравнивания для подписи осей; выбрать такую ориентацию поверхности, чтобы ее двумерное изображение было наиболее наглядным.
Дата: 2019-02-25, просмотров: 237.
