Элементы зонной теории кристаллов. Заполнение зон: металлы, диэлектрики, полупроводники. Электропроводность металлов. Электропроводность полупроводников. Примесные полупроводники. Магнитные свойства твердых тел. Контактные явления.
Тема 10. Физика атомного ядра и элементарных частиц
Состав ядра. Дефект масс и энергия связи ядра Свойства и природа ядерных сил. Радиоактивность. Закон радиоактивного превращения. Ядерные реакции и их типы. Реакция деления ядра. Реакции синтеза. Элементарные частицы и их классификация. Кварки. Типы и характеристики фундаментальных взаимодействий. Кванты фундаментальных полей. Физическая картина мира. Вещество и поле.
Основные формулы
Сила Ампера
в векторной форме:
,
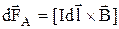в скалярной форме:
где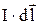 
– элемент тока, 
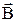– индукция магнитного поля, 
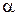– угол между векторами 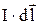и 
.
,
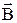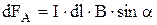Магнитный момент замкнутого контура площадью S с током I:
где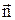 
– единичный вектор положительной нормали к плоскости контура, направление которого связано с направлением тока правилом правого винта.
,
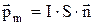Механический момент сил, действующих на контур с током, помещенный в магнитное поле с индукцией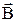
в векторной форме:
,
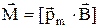в скалярной форме:
где 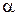– угол между векторам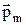и 
и .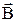
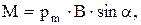
Сила Лоренца
в векторной форме:
,
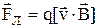в скалярной форме:
где q – заряд частицы,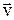 
– ее скорость, 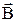– индукция магнитного поля, 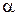– угол между векторам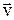и и .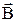
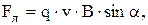
Закон Био-Савара-Лапласа
в векторной форме:
где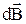 
– магнитная индукция поля, создаваемого элементом тока I 
; 
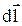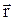– радиус-вектор точки, в которой определяется магнитная индукция; 
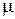– магнитная проницаемость окружающей проводник среды, 
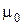– магнитная постоянная;
,
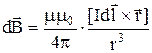в скалярной форме:
где 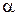– угол между векторами I 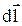и .
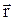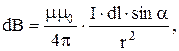
Индукция магнитного поля в центре кругового проводника (витка) с током I:
где r – радиус витка.
,
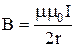Индукция магнитного поля, создаваемого бесконечно длинным прямым проводником с током I в точке, находящейся на расстоянии r от оси проводника:
.
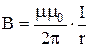Индукция магнитного поля, создаваемого отрезком проводника с током:
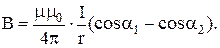
Индукция магнитного поля, создаваемого соленоидом с током I в средней его части (или тороидом на его оси):
где n – число витков, приходящихся на единицу длины соленоида.
,
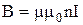Связь индукции 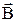с напряженностью 
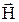магнитного поля (в случае однородной, изотропной среды):
.
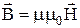Элементарный поток вектора индукции магнитного поля (магнитный поток) через площадку dS:
где 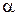– угол между направлением вектора 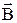и нормалью к площадке 
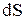, Вn – проекция вектора 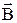на направление нормали к площадке.
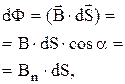
Поток вектора индукции магнитного поля через произвольную поверхность S:
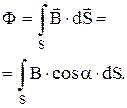
Потокосцепление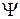 
(полный поток сквозь N витков):
.
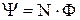Элементарная работа по перемещению контура с током I в магнитном поле:
где dФ – изменение магнитного потока, пронизывающего поверхность, ограниченную контуром.
,
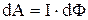Работа при произвольном перемещении контура в магнитном поле:
.
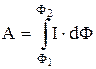Магнитный поток, сцепленный с соленоидом (катушкой содержащей N витков):
где L – индуктивность контура (коэффициент самоиндукции).
,
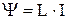Закон электромагнитной индукции (закон Фарадея - Максвелла):
где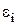 
– электродвижущая сила индукции, N – число витков контура.
,
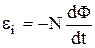Электродвижущая сила самоиндукции:
.
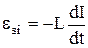Индуктивность соленоида:
где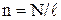 
– число витков на единицу длины соленоида, S – площадь сечения соленоида, 
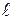– его длина, 
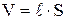– объем соленоида, 
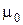– магнитная постоянная, 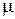– магнитная проницаемость среды.
,
,
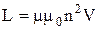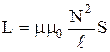Энергия магнитного поля соленоида (катушки) с индуктивностью L при силе тока I:
.
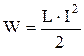Объемная плотность энергии магнитного поля:
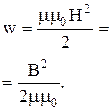
Скорость распространения электромагнитных волн (света) в среде:
где с – скорость света в вакууме,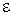 
– диэлектрическая проницаемость среды, 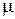– магнитная проницаемость среды, n – абсолютный показатель преломления среды.
,
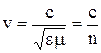Длина волны света в среде:
где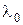 
– длина волны в вакууме, n – абсолютный показатель преломления среды.
,
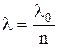Оптическая разность хода двух световых волн:
где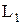 
и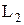 
– оптические длины путей световых волн в различных средах, 
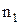и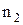 
– абсолютные показатели преломления сред, 
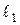и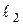 
– геометрические длины путей световых волн соответственно в средах с показателями преломления 
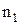и .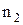
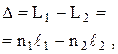
Связь разности фаз двух волн (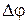 
) с их оптической разностью хода ( 
):
.
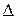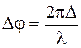Оптическая разность хода волн ( 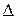), отраженных от верхней и нижней поверхностей тонкой плоскопараллельной пластинки или пленки, находящейся в воздухе:
а) в отраженном свете:
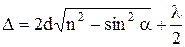
или
;
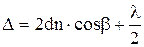б) в проходящем свете:
где d – толщина пластинки (пленки), 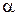– угол падения света на пластинку, 
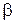– угол преломления, n – относительный показатель преломления материала пластинки (пленки).
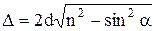
или
,
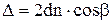Условие максимума интенсивности при интерференции двух когерентных волн:
где 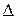– оптическая разность хода.
,
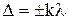k= 0, 1, 2, 3...,
Условие минимума интенсивности при интерференции двух когерентных волн:
,
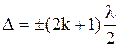k= 0, 1, 2, 3...
Положение максимумов и минимумов интенсивности света при интерференции волн от двух когерентных источников (метод Юнга):
где d – расстояние между двумя когерентными источниками (отверстиями в методе Юнга), находящимися на расстоянии L от экрана, параллельного обоим источникам, при условии L >> d.
,
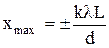k= 0, 1, 2, 3...,
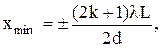
k= 0, 1, 2, 3...,
Ширина интерференционной полосы при интерференции волн от двух когерентных источников:
.
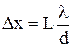Радиусы светлых колец Ньютона в отраженном свете (или темных в проходящем):
где k – номер кольца, R – радиус кривизны линзы.
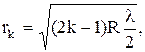
k = 1, 2, 3 ...,
Радиусы темных колец Ньютона в отраженном свете (или светлых в проходящем):
,
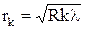k = 1, 2, 3 ...
Радиусы зон Френеля
для сферической волны:
,
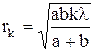для плоской волны:
где a – расстояние от диафрагмы с отверстием (щелью) до точечного источника света, b – расстояние от диафрагмы до точки наблюдения (экрана), k – номер зоны Френеля.
,
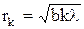При дифракции Френеля на круглом отверстии в центре экрана будет наблюдаться:
а) максимум интенсивности (светлое пятно), если в отверстие укладывается нечетное число зон Френеля;
б) минимум интенсивности (темное пятно), если в отверстие укладывается четное число зон Френеля.
Дифракция Фраунгофера на одной щели при нормальном падении лучей:
условие минимума интенсивности света:
,
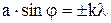k = 1, 2, 3, . . .
условие максимума интенсивности света:
где а – ширина щели,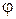 
– угол дифракции, k – номер максимума (минимума).
,
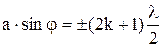k = 1, 2, 3, . . .
Положение главных максимумов при дифракции света на дифракционной решетке при нормальном падении лучей:
где d – период (постоянная) решетки, k – номер главного максимума (порядок спектра), 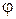– угол дифракции.
,
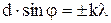k = 0, 1, 2, . . .,
Разрешающая способность дифракционной решетки:
где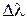 
– наименьшая разность длин волн двух соседних спектральных линий, видимых раздельно, N – общее число штрихов решетки, k – порядок спектра.
R =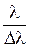 
= kN,
Угловая дисперсия дифракционной решетки:
где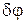 
– угловое расстояние между двумя спектральными линиями, отличающимися по длине волны на 
.
,
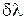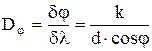Закон Брюстера:
где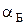 
– угол падения, при котором отраженный луч полностью поляризован, 
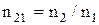– относительный показатель преломления.
,
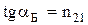Закон Малюса:
где I – интенсивность света, прошедшего через анализатор, I0 – интенсивность плоскополяризованного света, падающего на анализатор,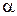 
– угол между плоскостью поляризации волны, падающей на анализатор, и плоскостью пропускания анализатора.
,
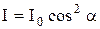Степень поляризации света:
где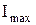 
и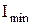 
– максимальная и минимальная интенсивности частично – поляризованного света, пропускаемого анализатором.
,
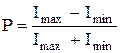Дата: 2019-02-25, просмотров: 184.
