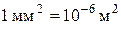ФИЗИКА
Часть 2
(Электромагнетизм, волновая оптика, элементы квантовой физики и физики твердого тела, элементы физики атомного ядра и элементарных частиц)
Методические указания и контрольные
задания для студентов заочной формы обучения
направлений 13.03.01; 13.03.02; 15.03.01; 15.03.04; 15.03.05;
20.03.01; 23.03.01; 23.03.03; 27.03.01; 23.05.01; 27.03.04
Курган 2018
Кафедра: «Общая физика»
Дисциплина: «Физика»
(направления 13.03.01; 13.03.02; 15.03.01; 15.03.04; 15.03.05;
20.03.01; 23.03.01; 23.03.03; 27.03.01; 23.05.01; 27.03.04).
Составили: д-р техн. наук, профессор Б.С. Воронцов,
канд. физ.-мат. наук, доцент Т.Н. Новгородова,
канд. физ.-мат. наук, доцент В.М. Овсянов.
Утверждены на заседании кафедры «21» февраля 2018 г.
Рекомендованы методическим советом университета «20» декабря 2017 г.
Введение
Физика – наука о наиболее простых и вместе с тем наиболее общих формах движения материи и их взаимных превращениях. Изучаемые физикой формы движения (механическая, тепловая и др.) присутствуют во всех высших и более сложных формах движения материи (химических, биологических и др.). Поэтому они, будучи наиболее простыми, являются в то же время наиболее общими формами движения материи.
Курс физики вместе с другими дисциплинами цикла общих математических и естественнонаучных дисциплин составляет основу теоретической подготовки инженеров и играет роль фундаментальной физико-математической базы, без которой невозможна успешная деятельность инженеров любого профиля.
Дисциплина «Физика» представляет собой целостный и фундаментальный курс, единый в своих частях и демонстрирующий роль физики как основы всего современного естествознания.
Изучение курса физики совместно с другими дисциплинами цикла способствует формированию у студентов знаний и умений, являющихся основой формирования соответствующих компетенций, а также современного естественнонаучного мировоззрения.
Цель настоящих методических указаний – оказать помощь студентам заочной формы обучения технических специальностей КГУ в изучении курса физики.
Общие методические указания
Дисциплина «Физика» изучается студентами технических специальностей заочной формы обучения Курганского государственного университета в течение двух семестров.
Основной формой обучения студента заочной формы обучения является самостоятельная работа с учебным материалом. Эта работа организуется и направляется кафедрой общей физики КГУ. Преподаватели кафедры читают студентам установочные и обзорные лекции, проводят консультации, практические и лабораторные занятия, осуществляют текущий и итоговый контроль приобретенных знаний.
Процесс изучения физики студентами заочной формы обучения в каждом из учебных семестров состоит из следующих этапов:
1) проработка установочных и обзорных лекций;
2) самостоятельная работа с учебниками и учебными пособиями;
3) выполнение и защита контрольных работ;
4) прохождение лабораторного практикума;
5) сдача зачетов (если они предусмотрены учебным планом) и экзаменов.
Важнейшим аспектом самостоятельной работы студентов является выполнение контрольных работ, которые позволяют закрепить теоретический материал курса. В процессе изучения физики студент должен выполнить две контрольные работы (по одной в семестр). Контрольные работы рецензируются преподавателем и, в случае необходимости, отправляются на доработку. Обязательным элементом является последующая защита контрольной работы студентом, которая может происходить как в течение семестра, так и во время сессии.
Основные разделы курса физики для инженерно-технических специальностей распределены по контрольным работам следующим образом.
Первая контрольная работа включает в себя физические основы механики, основы молекулярной физики и термодинамики, основы электродинамики.
Вторая – электромагнетизм, волновую оптику, элементы квантовой физики, элементы физики атомного ядра и элементарных частиц.
Вариант задания контрольной работы для каждого студента определяет преподаватель.
Перед её выполнением необходимо внимательно ознакомиться с примерами решения задач, уравнениями и формулами, а также со справочными материалами, приведенными в методических указаниях.
Каждая контрольная работа оформляется в отдельной тетради. На титульном листе должны быть указаны: номер контрольной работы, наименование дисциплины, фамилия и инициалы студента, номер учебной группы, шифр и домашний адрес.
При решении задач по физике необходимо:
1– Внимательно прочитать условие задачи. Полностью переписать условие задачи в тетрадь. Сделать краткую запись, выразить все данные в СИ. Если позволяет характер задачи, необходимо сделать рисунок, поясняющий ее сущность.
2– Уточнить, какие величины требуется найти в результате решения задачи. Дать определения этих величин, записать для них соответствующие математические соотношения.
3– Установить круг физических явлений, относящихся к данной задаче, и физические законы, лежащие в их основе. Записать в общем виде математические выражения этих законов, а также соотношения между величинами, характеризующими установленные явления с количественной точки зрения.
4– Переписать все уравнения в соответствии с условиями задачи. (Ввести обозначения величин, учесть начальные и конечные условия, число состояний и количественный состав представленной в задаче физической системы).
5– Исходя из полученных соотношений, составить замкнутую систему уравнений (число уравнений совпадает с числом неизвестных). Решить ее любым известным математическим методом. (Следует помнить, что в ряде случаев «лишние» неизвестные могут сокращаться в процессе промежуточных математических преобразований).
6– Если конечное выражение для искомой величины является достаточно сложным, то его правильность желательно проверить методом размерности.
7– Необходимо помнить, что численные значения физических величин всегда являются приближенными. Поэтому при расчетах надо руководствоваться правилами действий с приближенными числами.
Отметим, что для инженерных расчетов, как, впрочем, и для большинства физических, достаточна точность, обеспечиваемая тремя значащими цифрами.
8– Получив численный ответ, оценить его правдоподобность с позиций современной физики.
2 Содержание курса «Физика»
(2 семестр изучения)
Тема 6. Электромагнетизм
Магнитное поле. Вектор магнитной индукции. Сила Ампера. Сила Лоренца. Закон Био-Савара-Лапласа. Магнитный поток. Работа перемещения проводника и контура с током в магнитном поле. Теорема Остроградского-Гаусса. Закон полного тока для магнитного поля в вакууме. Явление электромагнитной индукции. Закон электромагнитной индукции. Явление самоиндукции. Индуктивность. Типы магнетиков. Энергия магнитного поля. Уравнения Максвелла.
Тема 7.Волновая оптика
Механизм образования волн. Гармонические волны. Уравнение электромагнитной волны. Основные свойства электромагнитных волн. Интерференция света и методы ее наблюдения. Дифракция и условия ее наблюдения. Принцип Гюйгенса-Френеля. Дифракция Френеля на круглом отверстии и диске. Дифракция Фраунгофера на одной щели и на дифракционной решетке. Поляризация света. Закон Малюса. Закон Брюстера. Поляроиды и поляризационные призмы.
Основные формулы
Сила Ампера
в векторной форме:
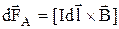 ,
,
в скалярной форме:
где 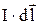 – элемент тока,
– элемент тока, 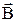 – индукция магнитного поля,
– индукция магнитного поля, 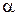 – угол между векторами
– угол между векторами 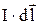 и
и 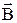 .
.
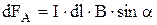 ,
,
Магнитный момент замкнутого контура площадью S с током I:
где 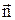 – единичный вектор положительной нормали к плоскости контура, направление которого связано с направлением тока правилом правого винта.
– единичный вектор положительной нормали к плоскости контура, направление которого связано с направлением тока правилом правого винта.
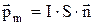 ,
,
Механический момент сил, действующих на контур с током, помещенный в магнитное поле с индукцией 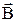
в векторной форме:
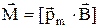 ,
,
в скалярной форме:
где 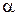 – угол между векторами
– угол между векторами 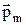 и
и 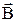 .
.
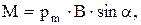
Сила Лоренца
в векторной форме:
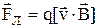 ,
,
в скалярной форме:
где q – заряд частицы, 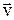 – ее скорость,
– ее скорость, 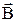 – индукция магнитного поля,
– индукция магнитного поля, 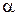 – угол между векторами
– угол между векторами 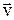 и
и 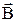 .
.
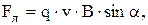
Закон Био-Савара-Лапласа
в векторной форме:
где 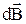 – магнитная индукция поля, создаваемого элементом тока I
– магнитная индукция поля, создаваемого элементом тока I 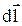 ;
; 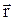 – радиус-вектор точки, в которой определяется магнитная индукция;
– радиус-вектор точки, в которой определяется магнитная индукция; 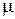 – магнитная проницаемость окружающей проводник среды,
– магнитная проницаемость окружающей проводник среды, 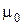 – магнитная постоянная;
– магнитная постоянная;
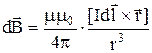 ,
,
в скалярной форме:
где 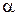 – угол между векторами I
– угол между векторами I 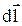 и
и 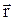 .
.
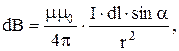
Индукция магнитного поля в центре кругового проводника (витка) с током I:
где r – радиус витка.
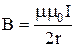 ,
,
Индукция магнитного поля, создаваемого бесконечно длинным прямым проводником с током I в точке, находящейся на расстоянии r от оси проводника:
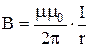 .
.
Индукция магнитного поля, создаваемого отрезком проводника с током:
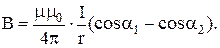
Индукция магнитного поля, создаваемого соленоидом с током I в средней его части (или тороидом на его оси):
где n – число витков, приходящихся на единицу длины соленоида.
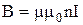 ,
,
Связь индукции 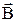 с напряженностью
с напряженностью 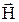 магнитного поля (в случае однородной, изотропной среды):
магнитного поля (в случае однородной, изотропной среды):
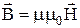 .
.
Элементарный поток вектора индукции магнитного поля (магнитный поток) через площадку dS:
где 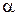 – угол между направлением вектора
– угол между направлением вектора 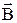 и нормалью к площадке
и нормалью к площадке 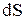 , Вn – проекция вектора
, Вn – проекция вектора 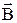 на направление нормали к площадке.
на направление нормали к площадке.
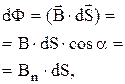
Поток вектора индукции магнитного поля через произвольную поверхность S:
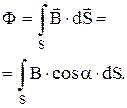
Потокосцепление 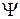 (полный поток сквозь N витков):
(полный поток сквозь N витков):
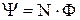 .
.
Элементарная работа по перемещению контура с током I в магнитном поле:
где dФ – изменение магнитного потока, пронизывающего поверхность, ограниченную контуром.
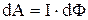 ,
,
Работа при произвольном перемещении контура в магнитном поле:
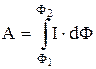 .
.
Магнитный поток, сцепленный с соленоидом (катушкой содержащей N витков):
где L – индуктивность контура (коэффициент самоиндукции).
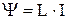 ,
,
Закон электромагнитной индукции (закон Фарадея - Максвелла):
где 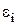 – электродвижущая сила индукции, N – число витков контура.
– электродвижущая сила индукции, N – число витков контура.
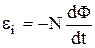 ,
,
Электродвижущая сила самоиндукции:
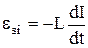 .
.
Индуктивность соленоида:
где 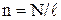 – число витков на единицу длины соленоида, S – площадь сечения соленоида,
– число витков на единицу длины соленоида, S – площадь сечения соленоида, 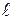 – его длина,
– его длина, 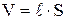 – объем соленоида,
– объем соленоида, 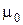 – магнитная постоянная,
– магнитная постоянная, 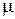 – магнитная проницаемость среды.
– магнитная проницаемость среды.
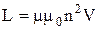 ,
,
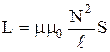 ,
,
Энергия магнитного поля соленоида (катушки) с индуктивностью L при силе тока I:
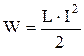 .
.
Объемная плотность энергии магнитного поля:
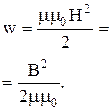
Скорость распространения электромагнитных волн (света) в среде:
где с – скорость света в вакууме, 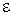 – диэлектрическая проницаемость среды,
– диэлектрическая проницаемость среды, 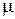 – магнитная проницаемость среды, n – абсолютный показатель преломления среды.
– магнитная проницаемость среды, n – абсолютный показатель преломления среды.
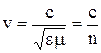 ,
,
Длина волны света в среде:
где 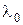 – длина волны в вакууме, n – абсолютный показатель преломления среды.
– длина волны в вакууме, n – абсолютный показатель преломления среды.
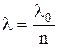 ,
,
Оптическая разность хода двух световых волн:
где 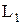 и
и 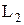 – оптические длины путей световых волн в различных средах,
– оптические длины путей световых волн в различных средах, 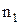 и
и 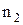 – абсолютные показатели преломления сред,
– абсолютные показатели преломления сред, 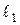 и
и 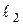 – геометрические длины путей световых волн соответственно в средах с показателями преломления
– геометрические длины путей световых волн соответственно в средах с показателями преломления 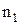 и
и 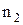 .
.
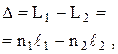
Связь разности фаз двух волн ( 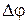 ) с их оптической разностью хода (
) с их оптической разностью хода ( 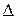 ):
):
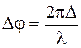 .
.
Оптическая разность хода волн ( 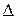 ), отраженных от верхней и нижней поверхностей тонкой плоскопараллельной пластинки или пленки, находящейся в воздухе:
), отраженных от верхней и нижней поверхностей тонкой плоскопараллельной пластинки или пленки, находящейся в воздухе:
а) в отраженном свете:
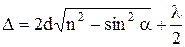
или
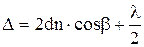 ;
;
б) в проходящем свете:
где d – толщина пластинки (пленки), 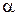 – угол падения света на пластинку,
– угол падения света на пластинку, 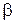 – угол преломления, n – относительный показатель преломления материала пластинки (пленки).
– угол преломления, n – относительный показатель преломления материала пластинки (пленки).
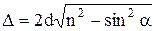
или
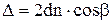 ,
,
Условие максимума интенсивности при интерференции двух когерентных волн:
где 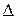 – оптическая разность хода.
– оптическая разность хода.
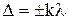 ,
,
k= 0, 1, 2, 3...,
Условие минимума интенсивности при интерференции двух когерентных волн:
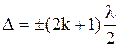 ,
,
k= 0, 1, 2, 3...
Положение максимумов и минимумов интенсивности света при интерференции волн от двух когерентных источников (метод Юнга):
где d – расстояние между двумя когерентными источниками (отверстиями в методе Юнга), находящимися на расстоянии L от экрана, параллельного обоим источникам, при условии L >> d.
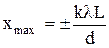 ,
,
k= 0, 1, 2, 3...,
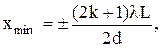
k= 0, 1, 2, 3...,
Ширина интерференционной полосы при интерференции волн от двух когерентных источников:
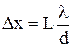 .
.
Радиусы светлых колец Ньютона в отраженном свете (или темных в проходящем):
где k – номер кольца, R – радиус кривизны линзы.
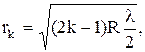
k = 1, 2, 3 ...,
Радиусы темных колец Ньютона в отраженном свете (или светлых в проходящем):
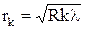 ,
,
k = 1, 2, 3 ...
Радиусы зон Френеля
для сферической волны:
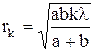 ,
,
для плоской волны:
где a – расстояние от диафрагмы с отверстием (щелью) до точечного источника света, b – расстояние от диафрагмы до точки наблюдения (экрана), k – номер зоны Френеля.
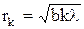 ,
,
При дифракции Френеля на круглом отверстии в центре экрана будет наблюдаться:
а) максимум интенсивности (светлое пятно), если в отверстие укладывается нечетное число зон Френеля;
б) минимум интенсивности (темное пятно), если в отверстие укладывается четное число зон Френеля.
Дифракция Фраунгофера на одной щели при нормальном падении лучей:
условие минимума интенсивности света:
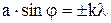 ,
,
k = 1, 2, 3, . . .
условие максимума интенсивности света:
где а – ширина щели, 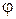 – угол дифракции, k – номер максимума (минимума).
– угол дифракции, k – номер максимума (минимума).
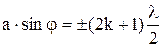 ,
,
k = 1, 2, 3, . . .
Положение главных максимумов при дифракции света на дифракционной решетке при нормальном падении лучей:
где d – период (постоянная) решетки, k – номер главного максимума (порядок спектра), 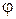 – угол дифракции.
– угол дифракции.
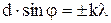 ,
,
k = 0, 1, 2, . . .,
Разрешающая способность дифракционной решетки:
где 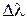 – наименьшая разность длин волн двух соседних спектральных линий, видимых раздельно, N – общее число штрихов решетки, k – порядок спектра.
– наименьшая разность длин волн двух соседних спектральных линий, видимых раздельно, N – общее число штрихов решетки, k – порядок спектра.
R = 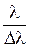 = kN,
= kN,
Угловая дисперсия дифракционной решетки:
где 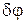 – угловое расстояние между двумя спектральными линиями, отличающимися по длине волны на
– угловое расстояние между двумя спектральными линиями, отличающимися по длине волны на 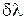 .
.
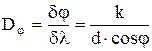 ,
,
Закон Брюстера:
где 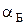 – угол падения, при котором отраженный луч полностью поляризован,
– угол падения, при котором отраженный луч полностью поляризован, 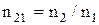 – относительный показатель преломления.
– относительный показатель преломления.
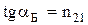 ,
,
Закон Малюса:
где I – интенсивность света, прошедшего через анализатор, I0 – интенсивность плоскополяризованного света, падающего на анализатор, 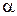 – угол между плоскостью поляризации волны, падающей на анализатор, и плоскостью пропускания анализатора.
– угол между плоскостью поляризации волны, падающей на анализатор, и плоскостью пропускания анализатора.
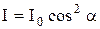 ,
,
Степень поляризации света:
где 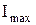 и
и 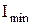 – максимальная и минимальная интенсивности частично – поляризованного света, пропускаемого анализатором.
– максимальная и минимальная интенсивности частично – поляризованного света, пропускаемого анализатором.
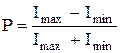 ,
,
Серия Лаймана:
n=1, k=2,3,4…
серия Бальмера:
n=2, k=3,4,5…
серия Пашена:
n=3, k=4,5,6,…
серия Брэкета:
n=4, k=5,6,7,…
Серия Пфунда:
n=5, k=6,7,8,…
серия Хэмфри:
n=6, k=7,8,9,…
Радиус n-й стационарной орбиты электрона в атоме водорода в модели Бора:
где m – масса электрона, e –элементарный заряд, 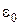 –электрическая постоянная, n=1, 2, …
–электрическая постоянная, n=1, 2, …
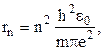
Период полураспада:
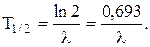
Среднее время жизни радиоактивного ядра:
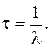
Активность нуклида (активность изотопа):
где 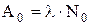 – активность изотопа в начальный момент времени (t=0).
– активность изотопа в начальный момент времени (t=0).
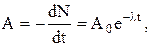
Правила смещения:
для 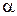 – распада:
– распада:
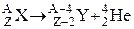 ,
,
для 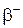 – распада:
– распада:
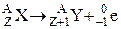 ,
,
для 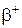 – распада:
– распада:
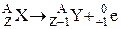 .
.
| Символическая запись ядерной реакции: где | 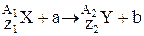 или
или
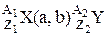 , ,
| |
Энергия ядерной реакции
(ее энергетический эффект):
где 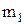 и и 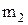 – массы покоя ядра мишени и бомбардирующей частицы; – массы покоя ядра мишени и бомбардирующей частицы; 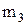 и и 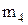 – массы покоя ядер (частиц) продуктов реакции. – массы покоя ядер (частиц) продуктов реакции.
|
| |
Примеры решения задач
Пример 1. Два параллельных бесконечно длинных тонких проводника, по которым текут в одном направлении токи I=60 А, расположены на расстоянии d = 10 см друг от друга. Определить магнитную индукцию 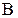 в точке, отстоящей от одного проводника на расстояние
в точке, отстоящей от одного проводника на расстояние 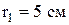 , а от другого – на
, а от другого – на 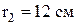 .
.
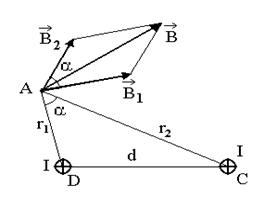
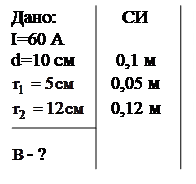 Решение
Решение
Для нахождения магнитной индукции в указанной точке А определим по правилу правого винта направления векторов индукций 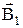 и
и 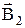 полей, создаваемых каждым проводником в отдельности (рисунок 1). По Рисунок 1.
полей, создаваемых каждым проводником в отдельности (рисунок 1). По Рисунок 1.
принципу суперпозиции:
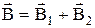 .
.
Модуль результирующего вектора 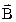 найдем по теореме косинусов:
найдем по теореме косинусов:
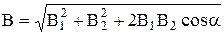 . (1)
. (1)
Значения индукций 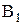 и
и 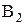 рассчитаем по формулам для индукции магнитного поля, создаваемого бесконечным прямым проводником с током:
рассчитаем по формулам для индукции магнитного поля, создаваемого бесконечным прямым проводником с током:
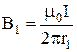 ,
, 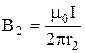 ,
,
где 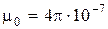 Гн/м – магнитная постоянная.
Гн/м – магнитная постоянная.
Подставляя эти выражения в (1) и вынося общий множитель за знак корня, получим:
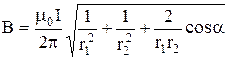 . (2)
. (2)
Из треугольника DAC несложно найти 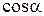 . По теореме косинусов в наших обозначениях:
. По теореме косинусов в наших обозначениях:
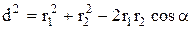 .
.
Отсюда 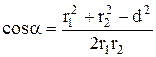 .
.
Подставляя данные, получим 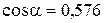 .
.
Подставив в формулу (2) значения всех входящих в нее величин, найдем искомую величину: В = 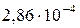 Тл.
Тл.
Пример 2. Плоский прямоугольный контур (рамка) со сторонами а=10 см и b = 15 см, по которому течет ток силой I=100 А, свободно установился в однородном магнитном поле (В=1 Тл). Определить: 1) работу 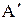 , совершаемую внешними силами при повороте контура на угол
, совершаемую внешними силами при повороте контура на угол 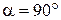 относительно оси, проходящей через середины его больших сторон; 2) среднюю ЭДС, возникающую при этом, если поворот совершается за две секунды. Считать, что при повороте контура сила тока в нем поддерживается неизменной.
относительно оси, проходящей через середины его больших сторон; 2) среднюю ЭДС, возникающую при этом, если поворот совершается за две секунды. Считать, что при повороте контура сила тока в нем поддерживается неизменной.
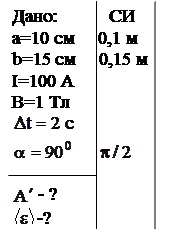 Решение
Решение
При перемещении контура с током в магнитном поле поле совершает работу:
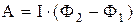 ,
,
где Ф1 – магнитный поток, пронизывающий контур до перемещения; Ф2 – то же, после перемещения, I – сила тока в контуре. Из закона сохранения энергии следует, что работа внешних сил:
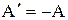 .
.
По определению магнитный поток: 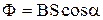 , где S – площадь контура,
, где S – площадь контура, 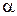 – угол между вектором индукции и магнитным моментом контура
– угол между вектором индукции и магнитным моментом контура 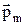 .
.
По условию задачи в начальном положении контур свободно установился в магнитном поле. Такое положение контура возможно, если векторы 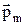 и
и 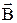 совпадают по направлению.
совпадают по направлению.
Тогда 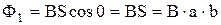 .
.
В конечном состоянии (после поворота на угол 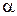 ) магнитный поток, пронизывающий контур:
) магнитный поток, пронизывающий контур:
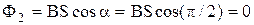 .
.
Следовательно
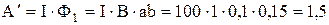 Дж.
Дж.
Среднее значение ЭДС найдем по закону Фарадея-Максвелла:
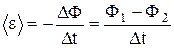 .
.
Подстановка данных приводит к результату: 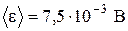 .
.
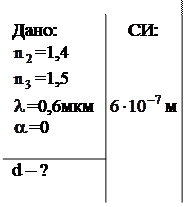
Пример 3. Толстая стеклянная пластинка покрыта тонкой пленкой и находится в воздухе. На нее падает нормально параллельный пучок монохроматического света с длиной волны 0,6 мкм. Отраженный свет максимально ослаблен вследствие интерференции. Определить толщину пленки, если показатель преломления стекла равен 1,5, а пленки – 1,4.
 Решение
Решение
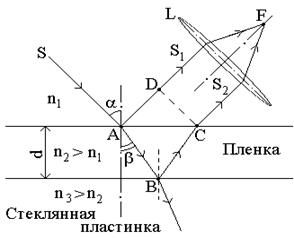
Рисунок 2.
Из световой волны, падающей на пленку, выделим узкий пучок SA. Ход этого пучка в случае, когда угол падения 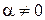 , показан на рисунке 2. В точках А и В пучок частично отражается и частично преломляется. Отраженные лучи света падают на собирающую линзу, пересекаются в ее фокусе и интерферируют между собой.
, показан на рисунке 2. В точках А и В пучок частично отражается и частично преломляется. Отраженные лучи света падают на собирающую линзу, пересекаются в ее фокусе и интерферируют между собой.
Так как показатель преломления воздуха ( 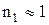 ) меньше показателя преломления вещества пленки (
) меньше показателя преломления вещества пленки ( 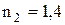 ), который, в свою очередь, меньше показателя преломления стекла (
), который, в свою очередь, меньше показателя преломления стекла ( 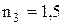 ), то в точках А и В отражение происходит от среды, оптически более плотной, чем среда, в которой идет падающая волна. При этом фаза колебаний обоих интерферирующих лучей при отражении изменяется на
), то в точках А и В отражение происходит от среды, оптически более плотной, чем среда, в которой идет падающая волна. При этом фаза колебаний обоих интерферирующих лучей при отражении изменяется на 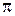 радиан, что приводит к уменьшению оптической длины пути каждого из пучков на
радиан, что приводит к уменьшению оптической длины пути каждого из пучков на 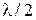 . Следовательно, результат интерференции этих лучей будет такой же, как если бы никакого изменения фазы колебаний ни у того, ни у другого луча не было.
. Следовательно, результат интерференции этих лучей будет такой же, как если бы никакого изменения фазы колебаний ни у того, ни у другого луча не было.
Как видно из рисунка 2, оптическая разность хода интерферирующих лучей равна:
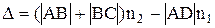 . (1)
. (1)
В результате интерференции лучи будут ослаблены, если выполняется условие минимума интенсивности:
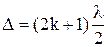 , (2)
, (2)
где k = 0, 1, 2 . . .
При угле падения 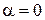 ,
, 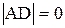 ,
, 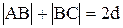 . Приравняв правые части уравнений (1) и (2), получим:
. Приравняв правые части уравнений (1) и (2), получим:
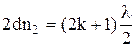 .
.
Отсюда искомая толщина пленки:
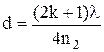 .
.
Полагая k=0, 1, 2, . . ., получим ряд возможных значений толщины пленки:
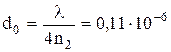 м;
м; 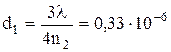 м и т.д.
м и т.д.
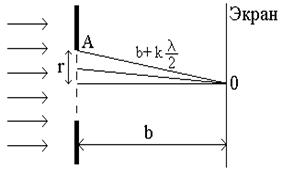
Пример 4. На диафрагму с круглым отверстием радиусом 1 мм падает нормально параллельный пучок света с длиной волны 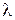 =0,5 мкм. На пути лучей, прошедших через отверстие, помещают экран. Определить максимальное расстояние от центра отверстия до экрана, при котором в центре дифракционной картины еще будет наблюдаться темное пятно.
=0,5 мкм. На пути лучей, прошедших через отверстие, помещают экран. Определить максимальное расстояние от центра отверстия до экрана, при котором в центре дифракционной картины еще будет наблюдаться темное пятно.
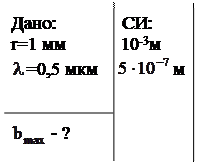 Решение
Решение
Рисунок 3.
При дифракции Френеля на круглом отверстии в центре дифракционной картины будет наблюдаться темное пятно, если в размер отверстия укладывается четное число зон Френеля.
Следовательно, разбив отверстие диафрагмы на зоны Френеля, расстояние АО от края отверстия до точки наблюдения (рисунок 3) можно записать в виде:
АО = 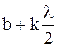 ,
,
где k = 2, 4, 6 . . . – число зон Френеля, укладывающихся в размер отверстия.
Тогда по теореме Пифагора:
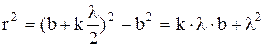 .
.
Так как 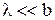 , то слагаемым, содержащим
, то слагаемым, содержащим 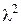 , можно пренебречь. Последнее равенство при этом перепишется в виде:
, можно пренебречь. Последнее равенство при этом перепишется в виде:
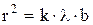 .
.
Отсюда 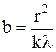 , где k = 2, 4, 6 . . .
, где k = 2, 4, 6 . . .
Очевидно, что максимальное значение b получится при k = 2:
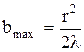 .
.
Произведя вычисления по последней формуле, найдем 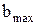 = 1 м.
= 1 м.
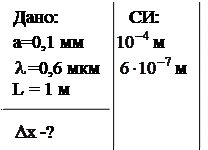
Пример 5. На щель шириной 0,1 мм нормально падает параллельный пучок света от монохроматического источника ( 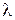 = 0,6 мкм). Определить ширину центрального максимума в дифракционной картине, проецируемой с помощью линзы, находящейся непосредственно за щелью, на экран, отстоящий от линзы на расстоянии L=1 м.
= 0,6 мкм). Определить ширину центрального максимума в дифракционной картине, проецируемой с помощью линзы, находящейся непосредственно за щелью, на экран, отстоящий от линзы на расстоянии L=1 м.
 Решение
Решение
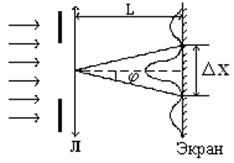
Центральный дифракционный максимум интенсивности света занимает область между ближайшими от него минимумами интенсивности. Поэтому ширину центрального максимума Рисунок 4.
примем равной расстоянию между этими двумя
минимумами (рисунок 4).
Минимумы интенсивности света при дифракции на одной щели наблюдаются под углами 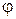 , определяемыми условием:
, определяемыми условием:
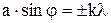 , (1)
, (1)
где k – порядок минимума. В нашем случае k =1.
Как видно из рисунка 4, 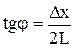 . Отсюда расстояние между двумя минимумами на экране:
. Отсюда расстояние между двумя минимумами на экране: 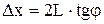 .
.
Так как при малых углах 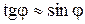 , то
, то
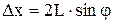 . (2)
. (2)
Выражая 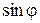 из формулы (1) и подставляя в (2), получим расчетную формулу:
из формулы (1) и подставляя в (2), получим расчетную формулу:
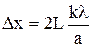 .
.
Произведя вычисления для k=1, получим 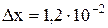 м.
м.
Пример 6. На дифракционную решетку нормально к ее поверхности падает параллельный пучок света с длиной волны 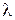 =0,5 мкм. Помещенная вблизи решетки линза проецирует дифракционную картину на плоский экран, удаленный от линзы на L=1 м. Расстояние между двумя максимумами интенсивности первого порядка, наблюдаемыми на экране, равно 20,2 см. Определить: 1) постоянную дифракционной решетки; 2) общее число максимумов, которое дает дифракционная решетка; 3) максимальный угол отклонения лучей, соответствующих последнему дифракционному максимуму.
=0,5 мкм. Помещенная вблизи решетки линза проецирует дифракционную картину на плоский экран, удаленный от линзы на L=1 м. Расстояние между двумя максимумами интенсивности первого порядка, наблюдаемыми на экране, равно 20,2 см. Определить: 1) постоянную дифракционной решетки; 2) общее число максимумов, которое дает дифракционная решетка; 3) максимальный угол отклонения лучей, соответствующих последнему дифракционному максимуму.
 |
 Решение
Решение
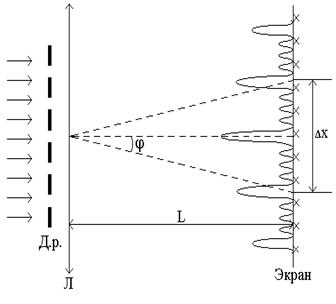
Рисунок 5.
1–Постоянная дифракционной решетки (d), длина волны ( 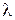 ) и угол отклонения лучей (
) и угол отклонения лучей ( 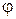 ), соответствующий k-му дифракционному максимуму, связаны соотношением:
), соответствующий k-му дифракционному максимуму, связаны соотношением:
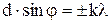 , (1)
, (1)
где k – порядок спектра или в случае монохроматического света порядок максимума. В данной задаче k=1.
Как видно из рисунка 5, 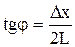 .
.
Ввиду того, что 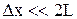 , можно считать, что угол
, можно считать, что угол 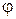 – мал. Тогда
– мал. Тогда 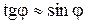 . С учетом этого соотношение (1) примет вид:
. С учетом этого соотношение (1) примет вид: 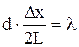 .
.
Тогда постоянная решетки: 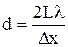 .
.
Подставляя данные, получим 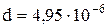 м.
м.
2–Дифракционная картина, наблюдаемая при дифракции на дифракционной решетке, состоит из центрального максимума (k=0) и расположенных симметрично по обе стороны от него максимумов более высоких порядков.
Найдем максимальное значение 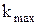 , исходя из того, что максимальный угол отклонения лучей решеткой не может превышать
, исходя из того, что максимальный угол отклонения лучей решеткой не может превышать 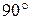 (рисунок 5).
(рисунок 5).
Из формулы (1):
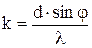 . (2)
. (2)
Подставив численные значения величин ( 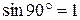 ), получим k = 9,9.
), получим k = 9,9.
Число k обязательно должно быть целым. В то же время оно не может принять значение равное 10, так как при этом значении 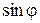 должен быть больше единицы, что невозможно. Следовательно,
должен быть больше единицы, что невозможно. Следовательно, 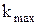 = 9.
= 9.
По обе стороны от центрального максимума будет наблюдаться по одинаковому числу максимумов, равному 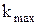 , т.е. всего 2
, т.е. всего 2 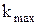 . Если учесть также центральный максимум, получим общее число максимумов: N = 2
. Если учесть также центральный максимум, получим общее число максимумов: N = 2 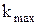 +1.
+1.
Подставляя значение 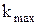 , найдем: N = 19.
, найдем: N = 19.
3–Для определения максимального угла отклонения лучей, соответствующего последнему дифракционному максимуму, выразим из соотношения (1) синус этого угла:
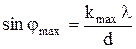 .
.
Отсюда 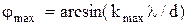 .
.
Подставив значения величин 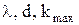 и произведя вычисления, получим:
и произведя вычисления, получим: 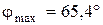 .
.
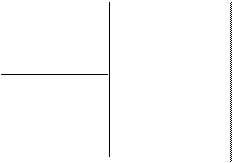
Пример 7. Определить длину волны 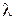 , массу и импульс фотона с энергией
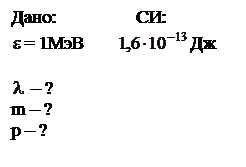
, массу и импульс фотона с энергией 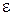 = 1 МэВ.
= 1 МэВ.
 Решение
Решение
Энергия фотона связана с длиной волны света соотношением: 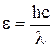 ,
,
где h – постоянная Планка, с – скорость света в вакууме. Отсюда 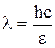 .
.
Подставив численные значения, получим: 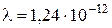 м.
м.
Массу фотона определим, используя формулу Эйнштейна 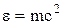 . Масса фотона
. Масса фотона 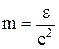 =
= 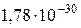 кг.
кг.
Импульс фотона 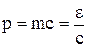 =
= 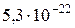 кг м/с.
кг м/с.
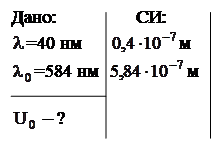
Пример 8. Натриевый катод вакуумного фотоэлемента освещается монохроматическим светом с длиной волны 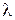 =40 нм. Определить задерживающее напряжение, при котором фототок прекращается. «Красная граница» фотоэффекта для натрия
=40 нм. Определить задерживающее напряжение, при котором фототок прекращается. «Красная граница» фотоэффекта для натрия 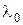 =584 нм.
=584 нм.
 Решение
Решение
Электрическое поле, препятствующее движению электронов от катода к аноду, называют обратным. Напряжение, при котором фототок полностью прекращается, называется задерживающим напряжением. При таком задерживающем напряжении 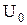 ни один из электронов, даже обладающий при вылете из катода максимальной скоростью
ни один из электронов, даже обладающий при вылете из катода максимальной скоростью 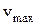 , не может преодолеть задерживающего поля и достигнуть анода. При этом начальная кинетическая энергия фотоэлектронов (
, не может преодолеть задерживающего поля и достигнуть анода. При этом начальная кинетическая энергия фотоэлектронов ( 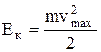 ) переходит в потенциальную (
) переходит в потенциальную ( 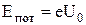 , где е=
, где е= 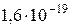 Кл – элементарный заряд, а
Кл – элементарный заряд, а 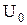 – наименьшее задерживающее напряжение). По закону сохранения энергии
– наименьшее задерживающее напряжение). По закону сохранения энергии
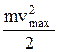 =
= 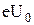 . (1)
. (1)
Кинетическую энергию электронов найдем, используя уравнение Эйнштейна для внешнего фотоэффекта:
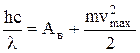 . (2)
. (2)
Отсюда 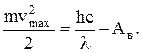 (3)
(3)
Работа выхода электронов Ав определяется красной границей фотоэффекта:
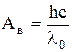 . (4)
. (4)
Подставив выражение (4) в уравнение (3), получим:
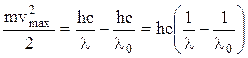 .
.
Тогда, из уравнения (1) 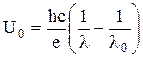 .
.
Вычисляя, получим 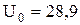 В.
В.
 Пример 9. Кинетическая энергия протона в четыре раза меньше его энергии покоя. Вычислить длину волны де Бройля для протона.
Пример 9. Кинетическая энергия протона в четыре раза меньше его энергии покоя. Вычислить длину волны де Бройля для протона.
Решение
Длина волны де Бройля определяется по формуле:
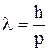 , (1)
, (1)
где h – постоянная Планка, 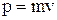 – импульс частицы.
– импульс частицы.
По условию задачи кинетическая энергия протона сравнима по величине с его энергией покоя Е0. Следовательно, импульс и кинетическая энергия связаны между собой релятивистским соотношением:
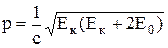 , (2)
, (2)
где с – скорость света в вакууме.
Используя условие задачи, получим: 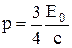 . Подставив полученное выражение в формулу (1), найдем длину волны де Бройля:
. Подставив полученное выражение в формулу (1), найдем длину волны де Бройля:
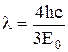 .
.
Энергию покоя протона найдем по формуле Эйнштейна 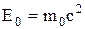 , где m0 – масса покоя протона, с – скорость света в вакууме.
, где m0 – масса покоя протона, с – скорость света в вакууме.
Подставив числовые значения, получим: 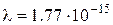 м.
м.
Пример 10. В результате перехода из одного стационарного состояния в другое атомом водорода был испущен квант с частотой 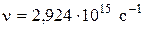 . Найти, как изменились радиус орбиты и скорость движения электрона, используя теорию Бора.
. Найти, как изменились радиус орбиты и скорость движения электрона, используя теорию Бора.
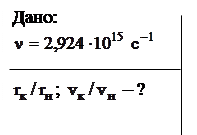 Решение
Решение
Излучение с частотой 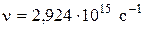 соответствует длине волны
соответствует длине волны 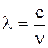 = 102,6 нм (с – скорость света в вакууме), лежащей в ультрафиолетовой области. Следовательно, спектральная линия принадлежит серии Лаймана, возникающей при переходе электрона на первый энергетический уровень (n=1).
= 102,6 нм (с – скорость света в вакууме), лежащей в ультрафиолетовой области. Следовательно, спектральная линия принадлежит серии Лаймана, возникающей при переходе электрона на первый энергетический уровень (n=1).
Используем обобщенную формулу Бальмера, чтобы определить номер энергетического уровня (k), с которого был совершен переход:
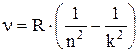 .
.
Выразим из этой формулы k:
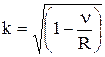 .
.
Подставляя имеющиеся данные, получим k=3. Следовательно, излучение произошло в результате перехода электрона с третьей орбиты на первую.
Значения радиусов 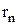 орбит и скоростей движения электронов
орбит и скоростей движения электронов 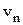 на этих орбитах найдем, рассмотрев движение электрона в атоме водорода.
на этих орбитах найдем, рассмотрев движение электрона в атоме водорода.
На электрон, находящийся на стационарной орбите в атоме водорода, со стороны ядра действует сила Кулона:
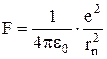 ,
,
которая сообщает ему нормальное ускорение 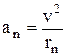 . Следовательно, согласно основному закону динамики:
. Следовательно, согласно основному закону динамики:
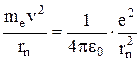 . (1)
. (1)
Кроме того, согласно постулату Бора, момент импульса электрона на стационарной орбите должен быть кратен постоянной Планка, т.е.
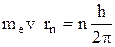 , (2)
, (2)
где n = 1, 2, 3 …. – номер стационарной орбиты.
Из уравнения (2) скорость 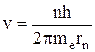 . Подставив это выражение в уравнение (1), получим
. Подставив это выражение в уравнение (1), получим
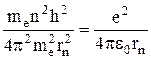 .
.
Отсюда радиус стационарной орбиты электрона в атоме водорода:
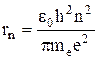 .
.
Тогда скорость электрона на этой орбите:
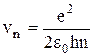 .
.
Принимая, что до излучения кванта электрон имел характеристики r3, v3, а после излучения r1, v1 несложно получить:
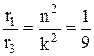 ;
; 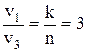 ,
,
то есть, радиус орбиты уменьшился в 9 раз, скорость электрона увеличилась в 3 раза.
Пример 11. Определить период полураспада радиоактивного изотопа, если известно, что за 1 сутки из 1 млн ядер распадается 175 тысяч.
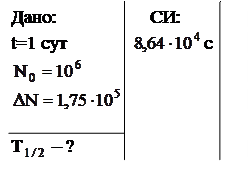 Решение
Решение
Период полураспада связан с постоянной радиоактивного распада соотношением:
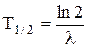 . (1)
. (1)
Постоянную радиоактивного распада 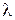 найдем, используя закон радиоактивного распада:
найдем, используя закон радиоактивного распада:
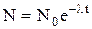 , (2)
, (2)
где N – число ядер, не распавшихся к моменту времени t, 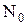 – начальное число ядер.
– начальное число ядер.
Разделив уравнение (2) на 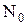 и прологарифмировав обе части, получим:
и прологарифмировав обе части, получим:
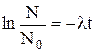 или
или 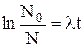 .
.
Отсюда: 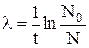 .
.
Учет того, что N= 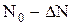 , дает:
, дает:
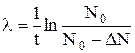 .
.
Подставив это выражение в (1), получим для периода полураспада следующее выражение:
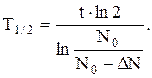
Подстановка численных значений и расчет приводят к результату 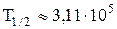 с.
с.
Примечание. Решая задачи подобного типа, допускается использование внесистемных единиц измерения времени, таких как – час, сутки, год.
Пример 12. Вычислить дефект массы, энергию связи и удельную энергию связи ядра 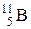 .
.
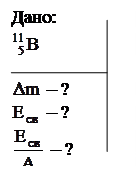 Решение
Решение
Дефект массы ядра определим по формуле:
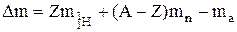 . (1)
. (1)
Для ядра 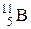 : Z=5; А=11.
: Z=5; А=11.
Вычисление дефекта массы выполним во внесистемных единицах – атомных единицах массы (а.е.м.). Необходимые данные возьмем из таблицы (приложение В):
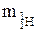 =1,00783 а.е.м.,
=1,00783 а.е.м., 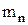 =1,00867 а.е.м.,
=1,00867 а.е.м., 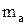 = 11,00931 а.е.м.
= 11,00931 а.е.м.
В результате расчета по формуле (1) получим: 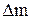 =0,08186 а.е.м.
=0,08186 а.е.м.
Энергию связи ядра найдем также во внесистемных единицах (МэВ), воспользовавшись формулой:
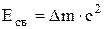 . (2)
. (2)
Коэффициент пропорциональности 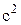 = 931,4 МэВ/а.е.м., т.е.
= 931,4 МэВ/а.е.м., т.е.
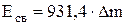 .
.
После подстановки численных значений получим: 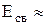 76,24 МэВ.
76,24 МэВ.
Удельная энергия связи, по определению, равна:
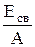
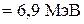 .
.
Примечание. Расчет дефекта массы ядра должен проводиться с максимально возможной точностью, т.е. с учетом всех значащих цифр, указанных в табличных данных.
Контрольная работа № 2
Таблица 1 – Таблица выбора вариантов индивидуального задания
| Вариант | |||||||||||
Номера задач
1–Два бесконечно длинных прямолинейных проводника с токами 6 А и 8 А скрещены перпендикулярно друг другу. Определить индукцию и напряженность магнитного поля на середине кратчайшего расстояния между проводниками, равного 20 см.
2–По двум бесконечно длинным прямолинейным параллельным проводникам, расстояние между которыми равно 15 см, в одном направлении текут токи 4 А и 6 А. Определить расстояние от проводника с меньшей силой тока до геометрического места точек, в которых индукция магнитного поля равна нулю.
3–По квадратной рамке течет ток силой I = 2 А. Напряженность магнитного поля в центре рамки равна H = 45 А/м. Определить периметр рамки.
4–По двум бесконечно длинным прямолинейным параллельным проводникам текут токи 5 и 10 А в одном направлении. Геометрическое место точек, в котором индукция магнитного поля равна нулю, находится на расстоянии 10 см от проводника с меньшей силой тока. Определить расстояние между проводниками.
5–По кольцевому проводнику радиусом 10 см течет ток I1 = 4 А. Параллельно плоскости кольцевого проводника на расстоянии 2 см от его центра проходит бесконечно длинный прямолинейный проводник, по которому течет ток I2 = 2 А. Определить индукцию и напряженность магнитного поля в центре кольца. Рассмотреть все возможные случаи.
6–Два круговых витка с током лежат в одной плоскости и имеют общий центр. Радиусы витков равны 12 и 8 см. Напряженность магнитного поля в центре витков равна 50 А/м, если токи текут в одном направлении, и нулю, если в противоположных. Определить силы токов, текущих по круговым виткам.
7–Бесконечно длинный прямолинейный проводник с током I1 = 3 А расположен на расстоянии 20 см от центра витка радиусом 10 см с током I2 = 1 А. Определить индукцию магнитного поля в центре витка для случаев, когда проводник: а) расположен перпендикулярно плоскости витка; б) находится в плоскости витка.
8–По квадратной рамке со стороной а = 0,2 м течет ток силой I = 4 А. Определить напряженность и индукцию магнитного поля в центре рамки.
9–По двум бесконечно длинным прямолинейным параллельным проводникам, расстояние между которыми 25 см, в противоположных направлениях текут токи 4 А и 6 А. Определить расстояние от проводника с большей силой тока до геометрического места точек, в которых индукция магнитного поля равна нулю.
10–По квадратной рамке со стороной а = 0,4 м течет ток, который создает в центре рами магнитное поле напряженностью H = 45 А/м. Определить силу тока в рамке.
11–Круговой проводящий контур радиусом r = 5 см и током I = 1 А находится в магнитном поле, причем плоскость контура перпендикулярна направлению поля. Напряженность поля равна 10 кА/м. Определить: 1) работу, которую необходимо совершить, чтобы повернуть контур на 900 вокруг оси, совпадающей диаметром контура и перпендикулярной к направлению поля; 2) среднюю ЭДС, индуцируемую в контуре, если поворот будет совершен за 6 секунд?
12–Круговой контур помещен в однородное магнитное поле так, что плоскость контура расположена под углом 300 к силовым линиям поля. Напряженность магнитного поля H = 2.104 А/м. По контуру течет ток силой 2А. Радиус контура 2 см. Какую работу надо совершить, чтобы повернуть контур на 900 вокруг оси, совпадающей с диаметром контура и перпендикулярной к направлению поля? Какая средняя ЭДС индуцируется в контуре, если поворот будет совершен за 12 секунд?
13–В однородном магнитном поле с индукцией В = 0,01 Тл находится прямой провод длиной L = 8 см, расположенный перпендикулярно линиям индукции. По проводу течет ток I = 2 A. Под действием сил поля за две секунды провод переместился на расстояние S = 5 см. Найти 1) работу сил поля; 2) разность потенциалов, индуцированную на концах провода.
14–Плоский контур, площадь которого S = 300 см2, находится в однородном магнитном поле с индукцией В = 0,01 Тл. Плоскость контура перпендикулярна линиям индукции. В контуре поддерживается неизменный ток I = 10 А. Определить работу А внешних сил по перемещению контура с током в область пространства, в которой магнитное поле отсутствует. Какая средняя ЭДС индуцируется в контуре, если это перемещение будет совершено за 2 секунды?
15–По проводу, согнутому в виде квадрата со стороной длиной а = 10 см, течет ток I = 20 А, сила которого поддерживается неизменной. Плоскость квадрата составляет угол 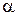 =200 c линиями индукции однородного магнитного поля (В=0,1Тл). Вычислить работу А, которую необходимо совершить для того, чтобы удалить провод за пределы поля. Какая средняя ЭДС индуцируется в проводе, если перемещение будет совершено за 2 с?
=200 c линиями индукции однородного магнитного поля (В=0,1Тл). Вычислить работу А, которую необходимо совершить для того, чтобы удалить провод за пределы поля. Какая средняя ЭДС индуцируется в проводе, если перемещение будет совершено за 2 с?
16–По кольцу радиусом R = 10 см, сделанному из тонкого гибкого провода, течет ток I = 100 A. Перпендикулярно плоскости кольца возбуждено магнитное поле с индукцией В = 0,1 Тл, совпадающей по направлению с индукцией В1 собственного магнитного поля кольца. Определить работу А внешних сил, которые, действуя на провод, деформировали его и придали ему форму квадрата. Сила тока при этом поддерживалась неизменной. Работой против упругих сил пренебречь. Определить среднюю ЭДС, возникшую при этом в замкнутом контуре, если изменение конфигурации произошло за 5 секунд?
17–Виток, по которому течет ток I = 20 А, свободно установился в однородном магнитном поле с индукцией В = 0,016 Тл. Диаметр витка равен 10 см. Определить работу А, которую нужно совершить, чтобы повернуть виток 1) на угол 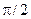 относительно оси, совпадающей с диаметром, 2) на угол
относительно оси, совпадающей с диаметром, 2) на угол 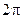 относительно этой же оси. Определить ЭДС в первом случае, если поворот был совершен за 3 секунды.
относительно этой же оси. Определить ЭДС в первом случае, если поворот был совершен за 3 секунды.
18. Прямой провод длиной L = 20 см с током I = 5 А, находящийся в однородном магнитном поле с индукцией В = 0,1 Тл, расположен перпендикулярно линиям магнитной индукции. Под действием сил поля проводник переместился на 2 см за 4 секунды. Определить: 1) работу сил поля; 2) разность потенциалов, возникшую на концах провода.
19–Квадратный проводящий контур со стороной l = 20 см и током I = 10 А свободно подвешен в однородном магнитном поле с индукцией В = 0,2 Тл. Определить: 1) работу, которую необходимо совершить, чтобы повернуть контур на 1800 вокруг оси, перпендикулярной направлению магнитного поля; 2) ЭДС, индуцированную в контуре, если поворот был совершен за 4 секунды.
20–В однородном магнитном поле с магнитной индукцией В = 0,2 Тл находится квадратный проводящий контур со стороной а = 20 см и током I = 10 А. Плоскость квадрата составляет с направлением поля угол 300. Определить работу удаления провода за пределы поля и ЭДС, возникшую в нем, если удаление было совершено за 7 секунд.
21–Соленоид содержит N = 1000 витков. Сила тока I в обмотке равна 1 А, магнитный поток Ф через поперечное сечение соленоида равен 0,1 мВб. Вычислить энергию магнитного поля внутри соленоида.
22–Сколько витков имеет катушка, индуктивность которой L = 1 мГн, если при токе I = 1 А магнитный поток сквозь сечение катушки Ф = 2 мкВб ?
23–Обмотка электромагнита имеет сопротивление R = 15 Ом и индуктивность L = 0,3 Гн. Определить время, за которое в обмотке выделится количество теплоты, равное энергии магнитного поля в сердечнике, если обмотка магнита находится под постоянным напряжением.
24–Сила тока I в обмотке соленоида, содержащего N = 1500 витков, равна 5 А. Магнитный поток Ф через поперечное сечение соленоида составляет 200 мкВб. Определить энергию магнитного поля в соленоиде.
25–Катушка длиной 20 см и диаметром D = 3 см имеет 400 витков. По катушке течет ток I = 2 А. Найти индуктивность L катушки и магнитный поток Ф, пронизывающий ее поперечное сечение.
26–Сколько витков проволоки диаметром 0,6 мм имеет однослойная обмотка катушки, индуктивность которой L=1 мГн и диаметр D = 4 см? Витки плотно прилегают друг к другу.
27–Соленоид индуктивностью L = 4 мГн содержит N = 600 витков. Площадь поперечного сечения соленоида S = 20 см2. Определить магнитную индукцию поля внутри соленоида, если сила тока, протекающего по его обмотке, равна 6 А.
28–Определить, сколько витков проволоки, вплотную прилегающих друг к другу, диаметром 0,5 мм с изоляцией ничтожной толщины надо намотать на картонный цилиндр диаметром 1,5 см, чтобы получить однослойную катушку индуктивностью L = 100 мкГн?
29–Катушка, намотанная на немагнитный цилиндрический каркас, имеет N1 = 750 витков и индуктивность L1 = 25 мГн. Чтобы увеличить индуктивность катушки до L2 = 36 мГн, обмотку с катушки сняли и заменили обмоткой из более тонкой проволоки с таким расчетом, чтобы длина катушки осталась прежней. Определить число N2 витков катушки после перемотки.
30–Соленоид длиной 50 см и площадью поперечного сечения S = 2 см2 имеет индуктивность L = 0,2 мкГн. При каком токе I объемная плотность энергии магнитного поля внутри соленоида w0 = 1 мДж/м3?
31–На пути одного из интерферирующих лучей помещается стеклянная пластинка толщиной 12 мкм. Определить, на сколько полос сместится интерференционная картина, если показатель преломления стекла n = 1,5; длина волны света 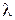 = 750 нм и свет падает на пластинку нормально.
= 750 нм и свет падает на пластинку нормально.
32–Какой должна быть толщина пластинки, изготовленной из стекла с показателем преломления n = 1,6, если при введении пластинки на пути одного из двух интерферирующих лучей интерференционная картина смещается на четыре полосы ? Длина волны падающего света 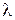 = 550 нм.
= 550 нм.
33–Во сколько раз в опыте Юнга (интерференция от двух точечных источников) нужно изменить расстояние до экрана, чтобы 5-я светлая полоса новой интерференционной картины оказалась на том же расстоянии от нулевой, что и 3-я светлая полоса в прежней картине.
34–В опыте Юнга (интерференция от двух точечных источников) вначале использовали свет с длиной волны 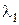 = 600 нм, а затем с
= 600 нм, а затем с 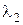 . Какова длина волны во втором случае, если 7-я светлая полоса в первом случае совпадает с 10-й темной во втором?
. Какова длина волны во втором случае, если 7-я светлая полоса в первом случае совпадает с 10-й темной во втором?
35–На мыльную пленку (n = 1,33), находящуюся в воздухе, падает под углом 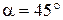 пучок лучей белого света. При какой наименьшей толщине пленки свет с длиной волны
пучок лучей белого света. При какой наименьшей толщине пленки свет с длиной волны 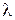 = 0,55 мкм окажется максимально усиленным в результате интерференции ? Наблюдение ведется в отраженном свете.
= 0,55 мкм окажется максимально усиленным в результате интерференции ? Наблюдение ведется в отраженном свете.
36–На мыльную пленку (n = 1,33), находящуюся в воздухе, падает под углом 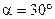 пучок лучей белого света. При какой наименьшей толщине пленки свет с длиной волны
пучок лучей белого света. При какой наименьшей толщине пленки свет с длиной волны 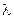 = 0,5 мкм окажется максимально ослабленным в результате интерференции? Наблюдение ведется в отраженном свете.
= 0,5 мкм окажется максимально ослабленным в результате интерференции? Наблюдение ведется в отраженном свете.
37–Во сколько раз увеличится расстояние между соседними интерференционными полосами на экране в опыте Юнга, если длину волны излучения изменили с 500 нм до 650 нм ?
38–На мыльную пленку (n = 1,33), находящуюся в воздухе, падает под углом 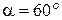 пучок лучей белого света. При какой наименьшей толщине пленки свет с длиной волны
пучок лучей белого света. При какой наименьшей толщине пленки свет с длиной волны 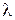 = 0,55 мкм окажется максимально усиленным в результате интерференции? Наблюдение ведется в проходящем свете.
= 0,55 мкм окажется максимально усиленным в результате интерференции? Наблюдение ведется в проходящем свете.
39–Расстояние между двумя когерентными источниками света ( 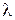 =0,5мкм) равно 0,1 мм. Расстояние между интерференционными максимумами в средней части интерференционной картины равно 1 см. Определить расстояние от источников до экрана.
=0,5мкм) равно 0,1 мм. Расстояние между интерференционными максимумами в средней части интерференционной картины равно 1 см. Определить расстояние от источников до экрана.
40–В воде интерферируют когерентные световые волны с частотой 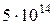 Гц. Усиление или ослабление света будет наблюдаться в точке наложения, если геометрическая разность хода лучей в ней равна 1,8 мкм? Показатель преломления воды n = 1,33.
Гц. Усиление или ослабление света будет наблюдаться в точке наложения, если геометрическая разность хода лучей в ней равна 1,8 мкм? Показатель преломления воды n = 1,33.
41–Дифракция наблюдается на расстоянии 1 м от точечного источника монохроматического света ( 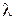 = 0,5 мкм). Посередине между источником света и экраном находится диафрагма с круглым отверстием. Определить радиус отверстия, при котором центр дифракционных колец на экране является наиболее темным.
= 0,5 мкм). Посередине между источником света и экраном находится диафрагма с круглым отверстием. Определить радиус отверстия, при котором центр дифракционных колец на экране является наиболее темным.
42–Сферическая волна, распространяющаяся из точечного монохроматического источника света ( 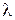 = 0,6 мкм ), встречает на своем пути экран с круглым отверстием радиусом 0,4 мм. Расстояние от источника до экрана равно 1 м. Определить наибольшее расстояние от отверстия до точки экрана, лежащей на линии, соединяющей источник с центром отверстия, где наблюдается максимум освещенности.
= 0,6 мкм ), встречает на своем пути экран с круглым отверстием радиусом 0,4 мм. Расстояние от источника до экрана равно 1 м. Определить наибольшее расстояние от отверстия до точки экрана, лежащей на линии, соединяющей источник с центром отверстия, где наблюдается максимум освещенности.
43–Плоская световая волна ( 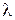 = 0,7 мкм) падает нормально на диафрагму с круглым отверстием радиусом 1,4 мм. Определить расстояния от диафрагмы до двух наиболее удаленных от нее точек, в которых наблюдаются минимумы интенсивности.
= 0,7 мкм) падает нормально на диафрагму с круглым отверстием радиусом 1,4 мм. Определить расстояния от диафрагмы до двух наиболее удаленных от нее точек, в которых наблюдаются минимумы интенсивности.
44–На щель шириной 0,1 мм падает нормально монохроматический свет с длиной волны 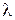 = 0,5 мкм. Дифракционная картина наблюдается на экране, расположенном параллельно щели. Определить расстояние от щели до экрана, если ширина центрального дифракционного максимума равна 1 см.
= 0,5 мкм. Дифракционная картина наблюдается на экране, расположенном параллельно щели. Определить расстояние от щели до экрана, если ширина центрального дифракционного максимума равна 1 см.
45–На щель шириной 2 мкм падает нормально параллельный пучок монохроматического света ( 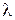 = 589 нм). Под какими углами будут наблюдаться дифракционные минимумы света?
= 589 нм). Под какими углами будут наблюдаться дифракционные минимумы света?
46–На щель шириной 0,1 мм падает нормально монохроматический свет ( 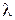 = 0,5 мкм). Что будет наблюдаться на экране (максимум или минимум интенсивности), если угол дифракции равен: 1) 17'; 2) 43'.
= 0,5 мкм). Что будет наблюдаться на экране (максимум или минимум интенсивности), если угол дифракции равен: 1) 17'; 2) 43'.
47–На дифракционную решетку, содержащую 400 штрихов на 1 мм, падает нормально монохроматический свет ( 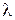 = 0,6 мкм). Найти общее число дифракционных максимумов, которые дает эта решетка. Определить угол дифракции, соответствующий последнему максимуму.
= 0,6 мкм). Найти общее число дифракционных максимумов, которые дает эта решетка. Определить угол дифракции, соответствующий последнему максимуму.
48–На дифракционную решетку нормально падает пучок света. Натриевая линия ( 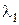 = 589 нм) наблюдается в спектре первого порядка при угле дифракции
= 589 нм) наблюдается в спектре первого порядка при угле дифракции 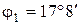 . Некоторая линия имеет в спектре второго порядка угол дифракции
. Некоторая линия имеет в спектре второго порядка угол дифракции 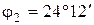 . Найти длину волны
. Найти длину волны 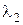 этой линии и число штрихов на единицу длины решетки.
этой линии и число штрихов на единицу длины решетки.
49–Постоянная дифракционной решетки d = 2 мкм. Какую разность длин волн 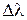 может разрешить эта решетка в области желтых лучей (
может разрешить эта решетка в области желтых лучей ( 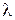 = 600 нм) в спектре второго порядка? Длина решетки – 2,5 см.
= 600 нм) в спектре второго порядка? Длина решетки – 2,5 см.
50–Дифракционная картина получена с помощью дифракционной решетки длиной 1,5 см и периодом d = 5 мкм. Определить, в спектре какого наименьшего порядка этой картины получатся раздельные изображения двух спектральных линий с разностью длин волн 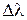 = 0,1 нм, если линии лежат в крайней красной части спектра (
= 0,1 нм, если линии лежат в крайней красной части спектра ( 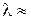 760 нм).
760 нм).
51–Сравнить энергию, массу и импульс фотонов красного ( 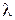 =0,7 мкм) и фиолетового (
=0,7 мкм) и фиолетового ( 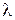 =0,4 мкм) излучений.
=0,4 мкм) излучений.
52–При какой температуре средняя кинетическая энергия теплового движения молекул одноатомного газа равна энергии фотона рентгеновских лучей ( 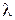 =0,1 нм)?
=0,1 нм)?
53–Найти массу фотона, импульс которого равен импульсу молекулы водорода при температуре 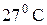 . Скорость молекулы считать равной средней квадратичной скорости.
. Скорость молекулы считать равной средней квадратичной скорости.
54–С какой скоростью должен двигаться электрон, чтобы его кинетическая энергия была равна энергии фотона с длиной волны 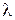 =520 нм?
=520 нм?
55–С какой скоростью должен двигаться электрон, чтобы его импульс был равен импульсу фотона с длиной волны 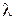 =520 нм?
=520 нм?
56–Какую энергию и частоту должен иметь фотон, чтобы его масса была равна массе покоя электрона?
57–При какой температуре средняя кинетическая энергия молекулы двухатомного газа будет равна энергии фотона с длиной волны 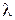 =
= 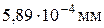 ? Чему равна масса этого фотона?
? Чему равна масса этого фотона?
58–Сколько фотонов в 1 с испускает электрическая лампочка накаливания, полезная мощность которой 25 Вт, если средняя длина волны излучения составляет 650 нм?
59–Определить длину волны фотона, импульс которого равен импульсу электрона, обладающего скоростью 10 Мм/с.
60–Чувствительность сетчатки глаза (наименьшая мощность излучения, еще воспринимаемая сетчаткой) к желтому свету с длиной волны 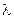 =600 нм составляет Р=
=600 нм составляет Р= 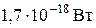 . Сколько фотонов должно падать ежесекундно на сетчатку, чтобы свет был воспринят?
. Сколько фотонов должно падать ежесекундно на сетчатку, чтобы свет был воспринят?
61–Фотоэлектроны, вырываемые с поверхности металла, полностью задерживаются при приложении обратного напряжения 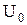 =3 В. Фотоэффект для этого металла начинается при частоте падающего монохроматического света
=3 В. Фотоэффект для этого металла начинается при частоте падающего монохроматического света 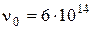 с
с 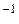 . Определить: 1) работу выхода электронов из этого металла; 2) частоту применяемого облучения.
. Определить: 1) работу выхода электронов из этого металла; 2) частоту применяемого облучения.
62–На поверхность литиевого катода падает монохроматическое излучение 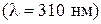 . Чтобы прекратить эмиссию электронов, нужно приложить задерживающую разность потенциалов U
. Чтобы прекратить эмиссию электронов, нужно приложить задерживающую разность потенциалов U 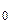 не менее 1,7 В. Определить работу выхода А и красную границу фотоэффекта.
не менее 1,7 В. Определить работу выхода А и красную границу фотоэффекта.
63–Для прекращения фотоэффекта, вызванного облучением ультрафиолетовым излучением платиновой пластинки, нужно приложить задерживающую разность потенциалов 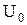 =3,7 В. Если платиновую пластинку заменить другой пластинкой, то задерживающую разность потенциалов придется увеличить до 6 В. Определить работу А выхода электронов с поверхности этой пластинки.
=3,7 В. Если платиновую пластинку заменить другой пластинкой, то задерживающую разность потенциалов придется увеличить до 6 В. Определить работу А выхода электронов с поверхности этой пластинки.
64–При облучении фотокатода видимым светом выбиваемые фотоэлектроны полностью задерживаются обратным напряжением 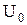 =1,2 В. Специальные измерения показали, что длина волны падающего света
=1,2 В. Специальные измерения показали, что длина волны падающего света 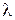 =400 нм. Определить красную границу фотоэффекта.
=400 нм. Определить красную границу фотоэффекта.
65–Найти частоту света, вырывающего с поверхности катода электроны, полностью задерживающиеся обратным напряжением в 3 В. Фотоэффект у этого металла начинается при частоте падающего света в 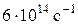 . Чему равна работа выхода электрона из этого металла.
. Чему равна работа выхода электрона из этого металла.
66–Плоский серебряный электрод освещается монохроматическим излучением с длиной волны 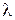 =83 нм. Определить, на какое максимальное расстояние от поверхности электрода может удалиться фотоэлектрон, если вне электрода имеется задерживающее электрическое поле напряженностью Е=10 В/см. Красная граница фотоэффекта для серебра
=83 нм. Определить, на какое максимальное расстояние от поверхности электрода может удалиться фотоэлектрон, если вне электрода имеется задерживающее электрическое поле напряженностью Е=10 В/см. Красная граница фотоэффекта для серебра 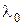 =264 нм.
=264 нм.
67–При освещении катода вакуумного фотоэлемента монохроматическим светом с длиной волны 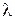 =310 нм фототок прекращается при некотором задерживающем напряжении. При увеличении длины волны на 25 % задерживающее напряжение оказывается меньше на 0,8 В. Определить по этим экспериментальным данным постоянную Планка.
=310 нм фототок прекращается при некотором задерживающем напряжении. При увеличении длины волны на 25 % задерживающее напряжение оказывается меньше на 0,8 В. Определить по этим экспериментальным данным постоянную Планка.
68. Какая доля энергии фотона (в %) израсходована на работу вырывания фотоэлектрона, если красная граница фотоэффекта 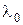 =307 нм и максимальная кинетическая энергия фотоэлектрона равна 1 эВ?
=307 нм и максимальная кинетическая энергия фотоэлектрона равна 1 эВ?
69–Катод вакуумного фотоэлемента, изготовленный из калия, освещается монохроматическим излучением с длиной волны 400 нм. Определить наименьшее задерживающее напряжение, при котором фототок прекратится. Работа выхода электронов из калия равна 2,2 эВ.
70–Определить постоянную Планка h, если известно, что фотоэлектроны, вырываемые с поверхности некоторого металла светом с частотой 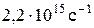 , полностью задерживаются обратным потенциалом в 6,6 В, а вырываемые светом с частотой
, полностью задерживаются обратным потенциалом в 6,6 В, а вырываемые светом с частотой 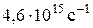 – потенциалом в 16,5 В.
– потенциалом в 16,5 В.
71–Протон движется в однородном магнитном поле с индукцией В=15 мТл по окружности радиусом R=1,4 м. Определить длину волны де Бройля для протона.
72–Найти длину волны де Бройля для электрона, движущегося по первой боровской орбите атома водорода.
73–Определить, какую ускоряющую разность потенциалов должен пройти протон, чтобы длина волны де Бройля для него была равна 1 пм.
74–Заряженная частица, ускоренная разностью потенциалов 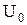 =500 В, имеет длину волны де Бройля
=500 В, имеет длину волны де Бройля 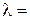 1,282 пм. Принимая заряд этой частицы равным заряду электрона, определить ее массу.
1,282 пм. Принимая заряд этой частицы равным заряду электрона, определить ее массу.
75–Вычислить длину волны де Бройля электрона и протона, обладающих кинетической энергией 1,00 кэВ. При каких значениях их кинетических энергий эта длина волны будет равна 100 пм?
76–При увеличении энергии электрона на 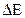 = 200 эВ длина волны де Бройля изменилась в 2 раза. Найти первоначальную длину волны де Бройля.
= 200 эВ длина волны де Бройля изменилась в 2 раза. Найти первоначальную длину волны де Бройля.
77–Найти длину волны де Бройля альфа-частицы, прошедшей ускоряющую разность потенциалов: 1) 1 кВ; 2) 1 МВ.
78–Электрон движется со скоростью 200 Мм/с. Определить длину волны де Бройля, учитывая изменение массы электрона в зависимости от скорости.
79–Найти кинетическую энергию электрона, при которой соответствующая длина волны де Бройля 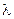 равна радиусу третьей боровской орбиты.
равна радиусу третьей боровской орбиты.
80–Определить длину волны де Бройля электрона, находящегося в атоме водорода на третьей боровской орбите.
81–Используя теорию Бора, определить, как изменилась кинетическая энергия электрона в атоме водорода при переходе его с четвертой орбиты на вторую.
82–Используя теорию Бора, определить частоту 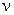 вращения электрона по третьей орбите атома водорода.
вращения электрона по третьей орбите атома водорода.
83–Атом водорода в основном состоянии поглотил квант света с длиной волны 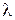 =121,5 нм. Используя теорию Бора, определить радиус r электронной орбиты возбужденного атома водорода.
=121,5 нм. Используя теорию Бора, определить радиус r электронной орбиты возбужденного атома водорода.
84–Атомарный водород находился в возбужденном состоянии. Определить: а) коротковолновую и длинноволновую границы его излучения, если n=4; б) к каким сериям принадлежат спектральные линии, соответствующие излучению таких атомов.
85–Используя теорию Бора для атома водорода, определить: а) радиус ближайшей к ядру орбиты; б) скорость движения электрона по этой орбите.
86–Используя теорию Бора, определить скорость v электрона по третьей орбите атома водорода.
87–Электрон находится на первой боровской орбите атома водорода. Определить для электрона: а) потенциальную энергию 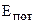 ; б) кинетическую энергию
; б) кинетическую энергию 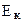 ; в) полную энергию
; в) полную энергию 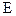 .
.
88–Используя теорию Бора, определить частоту фотона, излучаемого атомом водорода, при переходе электрона на уровень с номером n=2, если радиус орбиты электрона изменился в k=9 раз.
89–Используя теорию Бора, найти изменение кинетической энергии электрона в атоме водорода при излучении атомом фотона с длиной волны 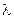 =486 нм.
=486 нм.
90–Вычислить длину волны 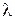 спектральной линии атомарного водорода, частота которой равна разности частот следующих двух линий серии Лаймана:
спектральной линии атомарного водорода, частота которой равна разности частот следующих двух линий серии Лаймана: 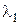 =102,60 нм и
=102,60 нм и 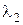 =97,27 нм. Какой серии принадлежит данная линия?
=97,27 нм. Какой серии принадлежит данная линия?
91–Какая часть начального количества атомов распадется за один год в радиоактивном изотопе тория 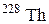 ?
?
92–Какая часть начального количества ядер актиния 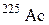 останется через 5 сут. ? через 15 сут. ?
останется через 5 сут. ? через 15 сут. ?
93–За один год начальное количество радиоактивного изотопа уменьшилось в три раза. Во сколько раз оно уменьшится за два года ?
94–За какое время распадется 1/4 начального количества ядер радиоактивного изотопа, если период его полураспада 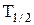 =24 ч ?
=24 ч ?
95–За время t=8 сут. распалось k=3/4 начального количества ядер радиоактивного изотопа. Определить период полураспада 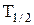 .
.
96–Сколько атомов полония распадется за сутки из 1 млн атомов ?
97–Сколько граммов радона распадется за 8 часов, если его начальная масса равняется 0,5 кг ?
98–Найти число распадов за 1 с в 1 г радия – 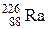 .
.
99–Период полураспада радиоактивного изотопа актиния 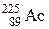 составляет 10 сут. Определить время, за которое распадется 1/3 начального количества ядер актиния.
составляет 10 сут. Определить время, за которое распадется 1/3 начального количества ядер актиния.
100–Определить период полураспада радиоактивного изотопа, если 5/8 начального количества ядер этого изотопа распалось за время t=849 с.
В задачах 101-110 найти дефект массы, энергию связи и удельную энергию связи ядер изотопов:
101–Лития 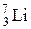 .
.
102–Гелия 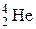 .
.
103–Алюминия 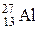 .
.
104–Кислорода 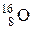 .
.
105–Водорода (дейтерия) 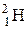 .
.
106–Азота 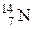 .
.
107–Кальция 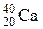 .
.
108–Меди 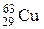 .
.
109–Кадмия 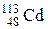 .
.
110–Урана 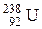 .
.
Список литературы
Основная учебная литература
1–Трофимова Т. И. Курс физики. – Москва : Высшая школа, 2003.
2–Савельев И. В. Курс физики. – Москва : АКТ, 2005. – Т. 1-5.
3–Чертов А. Г., Воробьев А. А. Задачник по физике. – Москва : Издательство физико-математической литературы, 2003.
4–Детлаф А. А., Яворский Б. М. Курс физики. – Москва : Издательский ценр «Академия», 2003.
5–Никеров В. А. Физика. Современный курс : учебник. – Москва : Издательско-торговая корпорация «Дашков и К°», 2012. – 452 с. – ЭБС «Консультант Студента».
Дополнительная учебная литература
1–Епифанов Г. И. Физика твердого тела. – Москва : Высшая школа, 1977.
2–Бордовский Г. А., Бурсиан Э. В. Общая физика : курс лекций. – Москва : Владос-Пресс, 2001. – Т. 1, 2.
3–Федосеев В. Б. Физика : учебник. – Ростов-на-Дону : Феникс, 2009.
4–Ландсберг Г. С. Оптика. – Москва : Физматлит, 2010.
5–Паршаков А. Н. Введение в квантовую физику : учеб. пособие. – Санкт-Петербург : Издательство «Лань», 2010.
Интернет-ресурсы
1 Физика для всех. URL : http://www.allphysics.ru
2 Федеральный интернет-экзамен. URL : http://www.fepo.ru
3 Открытая физика. URL : http://www.physics.ru
Приложения
Приложение А
Таблица А – Физические постоянные
| Название физической постоянной | Обозначение и величина |
| Скорость света в вакууме | 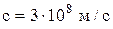
|
| Нормальное ускорение свободного падения | g = 9,81 м/с2 |
| Гравитационная постоянная | 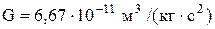
|
| Постоянная Авогадро | 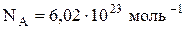
|
| Молярная газовая постоянная | 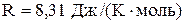
|
| Постоянная Больцмана | 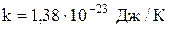
|
| Элементарный заряд | 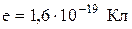
|
| Масса покоя электрона | 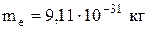
|
| Удельный заряд электрона | 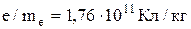
|
| Масса покоя нейтрона | 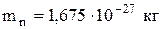
|
| Масса покоя протона | 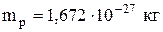
|
| Атомная единица массы | 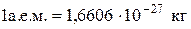
|
Масса изотопа 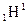
| 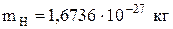
|
Приложение Б
Таблица Б – Единицы измерения физических величин (СИ) и их связь с внесистемными единицами
| Физическая величина | Рекомендуемые символы | Наименование единицы измерения | Обозначение единицы измерения | Некоторые внесистемные единицы | |
| 1 | 2 | 3 | 4 | 5 | |
|
Основные единицы | |||||
| Длина | l, L. | метр | м | 1 мм = 10-3 м 1 см = 10-2 м | |
| Масса | m, M | килограмм | кг | 1 г = 10-3 кг
1 т = 103 кг
1 а.е.м. = 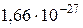 кг кг
| |
| Время | t, 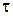
| секунда | с | 1 мин = 60 с 1 час = 3600 с | |
| Сила электрического тока | I, i | Ампер | А | ||
| Термодинамическая температура | T | Кельвин | К | 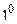 С = 1 К С = 1 К
| |
| Количество вещества | 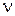
| моль | моль | ||
| Плоский угол | 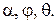
| радиан | рад | 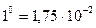 рад рад 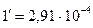 рад рад
| |
| Производные единицы | |||||
| Скорость | V, v, u | метр в секунду | м/с |
| |
| Ускорение | a | метр на секунду в квадрате | 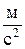
|
| |
| Частота | 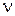 , n, f , n, f
| герц | Гц |
| |
| Частота вращения | n | оборот в секунду | 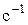
|
| |
| Циклическая частота | 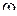
| секунда в минус первой степени | 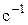
|
| |
| Работа, энергия | A, E, U | джоуль | Дж | 1 эВ=
| |
| Мощность | P, N | ватт | Вт | 1 л.с.=736 Вт | |
| Площадь | S | квадратный метр | 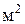
|
| |
Продолжение таблицы Б
| 1 | 2 | 3 | 4 | 5 |
| Объем | V | кубический метр | 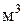
| 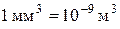
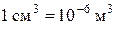
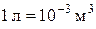
|
| Электрический заряд | Q, q | кулон | Кл | |
| Электрический потенциал, напряжение, ЭДС | 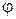 , U, , U, 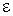
| вольт | В | |
| Электрическое сопротивление | R, r | ом | Ом | |
| Магнитный поток | Ф | вебер | Вб | |
| Магнитная индукция | В | тесла | Тл | |
| Напряженность магнитного поля | Н | ампер на метр | 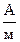
| |
| Индуктивность, взаимная индуктивность | L | генри | Гн | |
| Магнитный момент | р | ампер-квадратный метр | 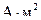
|
Приложение В – Справочные таблицы
Таблица В. 1 – Диэлектрическая проницаемость ( 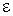 )
)
| Вода | 81 |
| Масло (трансформаторное) | 2,2 |
| Парафин | 2 |
| Слюда | 7 |
| Стекло | 7 |
| Фарфор | 5 |
| Эбонит | 3 |
Таблица В. 2 – Показатели преломления (n)
(средние значения для видимой части спектра)
| Алмаз | 2,42 |
| Вода | 1,33 |
| Сероуглерод | 1,63 |
| Скипидар | 1,48 |
| Слюда | 1,9 |
| Стекло | 1,5 - 1,9 |
Таблица В. 3 – Диапазоны электромагнитных волн
| Частота, Гц | Диапазон волн | Длина волн, м |
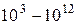
| Радиоволны | 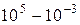
|
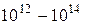
| Инфракрасный | 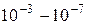
|
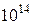
| Видимый свет | 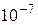
|
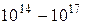
| Ультрафиолетовый | 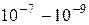
|
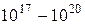
| Рентгеновский | 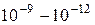
|
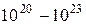
| 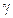 -излучение -излучение
| 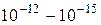
|
Таблица В. 4 – Работа выхода электронов
| Элемент | А. эВ | Элемент | А. эВ |
| Вольфрам | 4,5 | Платина | 5,3 |
| Калий | 2,2 | Серебро | 4,3 |
| Литий | 2,4 | Цинк | 4,2 |
| Оксид бария | 1,0 | Медь | 4,47 |
Таблица В. 5 – Масса покоя некоторых элементарных частиц и легких ядер
| Частица | Масса | |
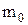 , кг , кг
| 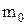 , а.е.м. , а.е.м.
| |
| Электрон (позитрон) | 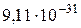
| 0,00055 |
| Протон | 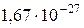
| 1,00728 |
| Нейтрон | 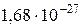
| 1,00867 |
| Дейтон | 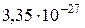
| 2,01355 |
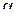 -частица -частица
| 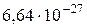
| 4,00149 |
Таблица В. 6 – Период полураспада радиоактивных изотопов
| Изотоп | Символ изотопа | Период полураспада |
| Актиний | 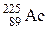
| 10 сут. |
| Йод | 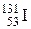
| 8,065 сут. |
| Иридий | 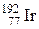
| 74,3 сут. |
| Радий | 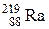
| 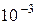 с. с.
|
| Радий | 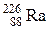
| 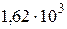 лет лет
|
| Радон | 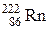
| 3,824 сут. |
| Торий | 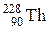
| 1,913 лет |
| Торий | 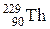
| 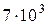 лет лет
|
| Полоний | 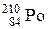
| 138,4 сут. |
Таблица В. 7 – Массы нейтральных атомов
| Элемент | Изотоп | Масса, а.е.м. |
| Водород | 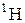
| 1,007825 |
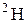
| 2,014102 | |
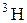
| 3,016049 | |
| Гелий | 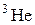
| 3,016030 |
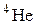
| 4,002604 | |
| Литий | 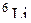
| 6,015126 |
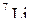
| 7,016005 | |
| Бериллий | 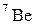
| 7,016931 |
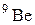
| 9,012186 | |
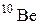
| 10,013535 |
Продолжение таблицы В. 7
| Бор | 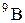
| 9,01333 |
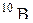
| 10,01294 | |
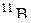
| 11,00931 | |
| Углерод | 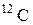
| 12,00000 |
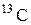
| 13,00335 | |
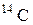
| 14,00324 | |
| Азот | 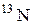
| 13,00574 |
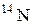
| 14,00307 | |
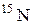
| 15,00011 | |
| Кислород | 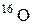
| 15,99491 |
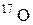
| 16,99913 | |
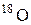
| 17,99916 | |
| Фтор | 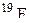
| 18,99840 |
| Магний | 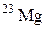
| 22,99414 |
| Алюминий | 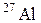
| 26,98154 |
| Фосфор | 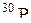
| 29,97832 |
| Калий | 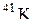
| 40,96184 |
| Кальций | 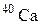
| 39,97542 |
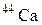
| 43,95549 | |
| Медь | 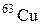
| 62,92959 |
| Кадмий | 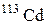
| 112,94206 |
| Уран | 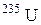
| 235,04393 |
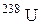
| 238,05076 |
Таблица В. 8 – Таблица десятичных приставок
| Приставка | Множитель | Обозначение | Приставка | Множитель | Обозначение |
| Тера | 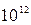
| Т | Санти | 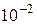
| с |
| Гига | 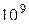
| Г | Милли | 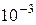
| м |
| Мега | 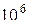
| М | Микро | 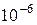
| мк |
| Кило | 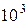
| К | Нано | 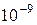
| н |
| Деци | 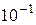
| Д | Пико | 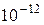
| п |
Воронцов Борис Сергеевич
Новгородова Татьяна Назаровна
Овсянов Виктор Михайлович
ФИЗИКА
Часть 2
(Электромагнетизм, волновая оптика, элементы квантовой физики и физики твердого тела, элементы физики атомного ядра и элементарных частиц)
Методические указания и контрольные
задания для студентов заочной формы обучения
направлений: 13.03.01; 13.03.02; 15.03.01; 15.03.04; 15.03.05;
20.03.01; 23.03.01; 23.03.03; 27.03.01; 23.05.01; 27.03.04.
Редактор Л. П. Чукомина
____________________________________________________________________
Подписано в печать Формат 60x84 1/16 Бумага 65 г/м2
Печать цифровая Усл. печ. л. Уч.-изд. л.
Заказ Тираж 100
____________________________________________________________________
БИЦ Курганского государственного университета.
640020, г. Курган, ул. Советская, 63/4.
Курганский государственный университет.
ФИЗИКА
Часть 2
(Электромагнетизм, волновая оптика, элементы квантовой физики и физики твердого тела, элементы физики атомного ядра и элементарных частиц)
Методические указания и контрольные
задания для студентов заочной формы обучения
направлений 13.03.01; 13.03.02; 15.03.01; 15.03.04; 15.03.05;
20.03.01; 23.03.01; 23.03.03; 27.03.01; 23.05.01; 27.03.04
Курган 2018
Кафедра: «Общая физика»
Дисциплина: «Физика»
(направления 13.03.01; 13.03.02; 15.03.01; 15.03.04; 15.03.05;
20.03.01; 23.03.01; 23.03.03; 27.03.01; 23.05.01; 27.03.04).
Составили: д-р техн. наук, профессор Б.С. Воронцов,
канд. физ.-мат. наук, доцент Т.Н. Новгородова,
канд. физ.-мат. наук, доцент В.М. Овсянов.
Утверждены на заседании кафедры «21» февраля 2018 г.
Рекомендованы методическим советом университета «20» декабря 2017 г.
Введение
Физика – наука о наиболее простых и вместе с тем наиболее общих формах движения материи и их взаимных превращениях. Изучаемые физикой формы движения (механическая, тепловая и др.) присутствуют во всех высших и более сложных формах движения материи (химических, биологических и др.). Поэтому они, будучи наиболее простыми, являются в то же время наиболее общими формами движения материи.
Курс физики вместе с другими дисциплинами цикла общих математических и естественнонаучных дисциплин составляет основу теоретической подготовки инженеров и играет роль фундаментальной физико-математической базы, без которой невозможна успешная деятельность инженеров любого профиля.
Дисциплина «Физика» представляет собой целостный и фундаментальный курс, единый в своих частях и демонстрирующий роль физики как основы всего современного естествознания.
Изучение курса физики совместно с другими дисциплинами цикла способствует формированию у студентов знаний и умений, являющихся основой формирования соответствующих компетенций, а также современного естественнонаучного мировоззрения.
Цель настоящих методических указаний – оказать помощь студентам заочной формы обучения технических специальностей КГУ в изучении курса физики.
Общие методические указания
Дисциплина «Физика» изучается студентами технических специальностей заочной формы обучения Курганского государственного университета в течение двух семестров.
Основной формой обучения студента заочной формы обучения является самостоятельная работа с учебным материалом. Эта работа организуется и направляется кафедрой общей физики КГУ. Преподаватели кафедры читают студентам установочные и обзорные лекции, проводят консультации, практические и лабораторные занятия, осуществляют текущий и итоговый контроль приобретенных знаний.
Процесс изучения физики студентами заочной формы обучения в каждом из учебных семестров состоит из следующих этапов:
1) проработка установочных и обзорных лекций;
2) самостоятельная работа с учебниками и учебными пособиями;
3) выполнение и защита контрольных работ;
4) прохождение лабораторного практикума;
5) сдача зачетов (если они предусмотрены учебным планом) и экзаменов.
Важнейшим аспектом самостоятельной работы студентов является выполнение контрольных работ, которые позволяют закрепить теоретический материал курса. В процессе изучения физики студент должен выполнить две контрольные работы (по одной в семестр). Контрольные работы рецензируются преподавателем и, в случае необходимости, отправляются на доработку. Обязательным элементом является последующая защита контрольной работы студентом, которая может происходить как в течение семестра, так и во время сессии.
Основные разделы курса физики для инженерно-технических специальностей распределены по контрольным работам следующим образом.
Первая контрольная работа включает в себя физические основы механики, основы молекулярной физики и термодинамики, основы электродинамики.
Вторая – электромагнетизм, волновую оптику, элементы квантовой физики, элементы физики атомного ядра и элементарных частиц.
Вариант задания контрольной работы для каждого студента определяет преподаватель.
Перед её выполнением необходимо внимательно ознакомиться с примерами решения задач, уравнениями и формулами, а также со справочными материалами, приведенными в методических указаниях.
Каждая контрольная работа оформляется в отдельной тетради. На титульном листе должны быть указаны: номер контрольной работы, наименование дисциплины, фамилия и инициалы студента, номер учебной группы, шифр и домашний адрес.
При решении задач по физике необходимо:
1– Внимательно прочитать условие задачи. Полностью переписать условие задачи в тетрадь. Сделать краткую запись, выразить все данные в СИ. Если позволяет характер задачи, необходимо сделать рисунок, поясняющий ее сущность.
2– Уточнить, какие величины требуется найти в результате решения задачи. Дать определения этих величин, записать для них соответствующие математические соотношения.
3– Установить круг физических явлений, относящихся к данной задаче, и физические законы, лежащие в их основе. Записать в общем виде математические выражения этих законов, а также соотношения между величинами, характеризующими установленные явления с количественной точки зрения.
4– Переписать все уравнения в соответствии с условиями задачи. (Ввести обозначения величин, учесть начальные и конечные условия, число состояний и количественный состав представленной в задаче физической системы).
5– Исходя из полученных соотношений, составить замкнутую систему уравнений (число уравнений совпадает с числом неизвестных). Решить ее любым известным математическим методом. (Следует помнить, что в ряде случаев «лишние» неизвестные могут сокращаться в процессе промежуточных математических преобразований).
6– Если конечное выражение для искомой величины является достаточно сложным, то его правильность желательно проверить методом размерности.
7– Необходимо помнить, что численные значения физических величин всегда являются приближенными. Поэтому при расчетах надо руководствоваться правилами действий с приближенными числами.
Отметим, что для инженерных расчетов, как, впрочем, и для большинства физических, достаточна точность, обеспечиваемая тремя значащими цифрами.
8– Получив численный ответ, оценить его правдоподобность с позиций современной физики.
2 Содержание курса «Физика»
(2 семестр изучения)
Тема 6. Электромагнетизм
Магнитное поле. Вектор магнитной индукции. Сила Ампера. Сила Лоренца. Закон Био-Савара-Лапласа. Магнитный поток. Работа перемещения проводника и контура с током в магнитном поле. Теорема Остроградского-Гаусса. Закон полного тока для магнитного поля в вакууме. Явление электромагнитной индукции. Закон электромагнитной индукции. Явление самоиндукции. Индуктивность. Типы магнетиков. Энергия магнитного поля. Уравнения Максвелла.
Тема 7.Волновая оптика
Механизм образования волн. Гармонические волны. Уравнение электромагнитной волны. Основные свойства электромагнитных волн. Интерференция света и методы ее наблюдения. Дифракция и условия ее наблюдения. Принцип Гюйгенса-Френеля. Дифракция Френеля на круглом отверстии и диске. Дифракция Фраунгофера на одной щели и на дифракционной решетке. Поляризация света. Закон Малюса. Закон Брюстера. Поляроиды и поляризационные призмы.
Тема 8. Элементы квантовой физики
Тепловое излучение, его характеристики. Квантовая гипотеза и формула Планка. Внешний фотоэффект. Уравнение Эйнштейна для внешнего фотоэффекта. Фотоны.
Гипотеза де Бройля. Соотношения неопределенностей. Волновая функция. Стационарное уравнение Шредингера. Постулаты Бора. Линейчатые спектры атомов (по Бору). Водородоподобные атомы в квантовой механике. Принцип Паули. Периодическая система элементов.
Дата: 2019-02-25, просмотров: 413.
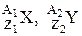 – исходное и конечное ядра, соответственно, с зарядовыми числами
– исходное и конечное ядра, соответственно, с зарядовыми числами 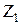 и
и 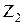 и массовыми числами
и массовыми числами 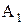 и
и 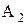 ; а и b – соответственно; бомбардирующая и испускаемая (или испускаемые) в ядерной реакции частицы.
; а и b – соответственно; бомбардирующая и испускаемая (или испускаемые) в ядерной реакции частицы. 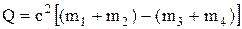 ,
,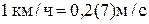
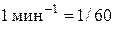 с-1
с-1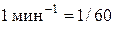 с-1
с-1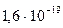 Дж
Дж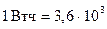 Дж
Дж