Обработка собранных мнений (данных) экспертов проводится как количественно (численные данные), так и качественно (содержательная информация). При обработке используются различные способы.
При наличии численных данных для решения вопросов, имеющих достаточный информационный материал, применяются методы усреднения экспертных суждений. Однако даже при имеющихся численных данных, но при недостаточности информации по решаемому вопросу (что нередко бывает при проектировании СК), наряду с количественными методами обработки экспертных данных используются методы качественного анализа и синтеза.
При использовании рассмотренных экспертных методов (рангов и др.) мнения экспертов часто не совпадают, поэтому необходимо количественно оценивать меру согласованности мнений экспертов и определять причины несовпадения суждений. Мера согласованности, естественно, определяется на основе статистических данных всей группы экспертов. Для оценки меры согласованности мнений экспертов используются, как правило, коэффициенты конкордации.
Мера согласованности определяется математико-статистической обработкой всех имеющихся результатов экспертизы. Так, согласованность мнений компетентных экспертов при использовании всех указанных экспертных методов, где определяются ранги объектов, можно определить с помощью коэффициента конкордации (согласия) по формуле:
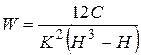
где С — сумма квадратов отклонений сумм рангов по каждому объекту от средней суммы рангов по всем объектам и экспертам, т. е.
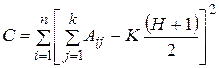
где 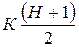 – средняя сумма рангов.
– средняя сумма рангов.
Полная запись формулы имеет следующий вид:
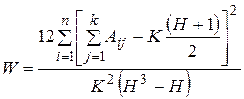
Коэффициент конкордации W может быть в диапазоне 1 ≥ W ≥ 0. При W=0 согласованность мнений экспертов отсутствует, а при W=1 согласованность полная. Обычно считается, что согласованность вполне достаточна, если W ≥ 0,5.
Допустим, по результатам работы компетентных экспертов получены определенные данные ранжирования и по ним требуется рассчитать коэффициент конкордации (табл. 7.5.1).
Таблица 8.5.1 Данные для расчета коэффициента конкордации
| Эксперт № К=6 | Ранги, поставленные экспертами пяти объектам ранжирования (Н = 5) | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 4 | 5 | 2 | 1 | 3 |
| 2 | 3 | 5 | 1 | 2 | 4 |
| 3 | 4 | 5 | 3 | 1 | 2 |
| 4 | 3 | 5 | 2 | 4 | 1 |
| 5 | 4 | 3- | 2 | 1 | 5 |
| 6 | 4 | 5 | 2 | 1 | 3 |
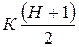
| 18 | 18 | 18 | 18 | 18 |
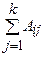
| 22 | 28 | 12 | 10 | 18 |
| С | 16 | 100 | 36 | 64 | 0 |
Коэффициент конкордации равен:

т. е. мнения экспертов можно признать согласованными, так как полученная величина коэффициента конкордации удовлетворяет условию W ≥ 0,5.
При использовании экспертных методов, в которых ранги не определяются, для нахождения конкордации рассчитанные значимости объектов следует переводить в ранги. Ранг 1 приписывается объекту, у которого значимость наибольшая и т. д., в противном случае оценку согласованности мнений проводят по другим критериям согласия.
Рассчитанную величину коэффициента конкордации взвешивают по критерию Пирсона (X2) с определенным уровнем значимости (В), т. е. максимальной вероятностью неправильного результата работы экспертов. Обычно задавать значимость достаточно в пределах 0,005 - 0,05.
В случае получения расчетной величины Х2расч > табличной Х2табл (с избранным уровнем значимости) мнения экспертов окончательно признаются согласованными
Табличные величины Х2табл зависят от принимаемого уровня значимости (в таблице 7.5.2 - 0,05) и числа степеней свободы (S), которое определяют по формуле:
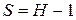
Расчетная величина Х2расч, определяется по формуле:
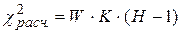
Таким образом, для данных приведенного ранее примера:
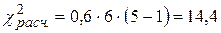
При уровне значимости 0,05 табличная величина Х2табл равна примерно 9, т. е. мнения экспертов можно окончательно признать с вероятностью 0,95 согласованными, так как Х2расч > Х2табл.
Таблица 8.5.2 Распределение Пирсона (Х2табл - распределение), значения Х2табл для вероятности Р=95% (уровень значимости В =0,05)
| S | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Х 2табл | 3,841 | 5,991 | 7,815 | 9,488 | 11,070 | 12,592 | 14,067 | 15,507 | 16,919 | 18,307 |
| S | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Х2табл | 19,675 | 21,026 | 22,362 | 23,685 | 24,996 | 26,296 | 27,587 | 28,869 | 30,144 | 31,410 |
| S | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| Х2табл | 35,479 | 36,781 | 38,076 | 39,384 | 40,046 | 41,923 | 43,194 | 44,461 | 45,722 | 46,979 |
В случае определения несогласованности мнений экспертов по коэффициентам конкордации и соответствующей проверке его величины по критерию Пирсона экспертные опросы следует осуществить повторно.
Обработка экспертных и социологических данных и расчеты мер согласованности требуют довольно трудоемких вычислений, поэтому при проведении сбора и обработки результатов экспертной и социологической информации следует шире использовать компьютерную технику.
Применение всех рассмотренных экспертных методов, несмотря на их недостатки, при исследованиях и проектировании систем УК показывает их эффективность, причем наибольший эффект достигается при одновременном использовании как рассмотренных выше методов, так и других.
Дата: 2019-02-19, просмотров: 348.