Задача 1. Расчёт затрат
Производство и затраты фирмы
Заполните таблицу на основании следующих данных о затратах фирмы в краткосрочном периоде:
| Q | AFC | VC | AC | MC | TC |
| 0 | |||||
| 1 | 8 | ||||
| 2 | 4 | ||||
| 3 | 2 | 15 | |||
| 4 | 11 |
Решение:
Расшифровка обозначений, определения и формулы подробно рассмотрены в задаче №71.
Начнём заполнение таблицы с нахождения общих издержек при Q = 1:
АС(1) = TC(1) / Q = 8
Отсюда:
TC(1) = 8
TC(2) = TC(1) + MC(2) = 8 + 4 = 12
FC = AFC × Q = 2 × 3 = 6 для любого Q.
Заполним первый столбец:
AFC(1) = 6 / 1 = 6
AFC(2) = 6 / 2 =3
AFC(4) = 6 / 4 =1,5
При Q = 0 TC(0) = FC = 6
MC(1) = TC(1) - TC(0) = 8 - 6 = 2
AC(2) = TC(2) / 2 = 12 / 2 = 6
AC(3) = TC(3) / 3 = 15 / 3 = 5
MC(3) = TC(3) - TC(2) = 15 - 12 = 3
TC(4) = FC + VC(4) = 6 + 11 = 17
MC(4) = TC(4) - TC(3) = 17 - 15 = 2
AC(4) = TC(4) / 4 = 17 / 4 = 4,25
Осталось заполнить столбец переменных издержек:
VC(0) = 0
VC(1) = TC(1) - FC = 8 - 6 = 2
VC(2) = TC(2) - FC = 12 - 6 = 6
VC(3) = TC(3) - FC = 15 - 6 = 9
Заполним таблицу:
| Q | AFC | VC | AC | MC | TC |
| 0 | - | 0 | - | - | 6 |
| 1 | 6 | 2 | 8 | 2 | 8 |
| 2 | 3 | 6 | 6 | 4 | 12 |
| 3 | 2 | 9 | 5 | 3 | 15 |
| 4 | 1,5 | 11 | 4,25 | 2 | 17 |
Задача 2. Расчёт издержек фирмы
Производство и затраты фирмы
Информация о деятельности фирмы, кроме представленной в таблице, оказалась утраченной. Восстановите недостающую информацию об издержках фирмы.
| Q | TC | VC | FC | AC | AVC | AFC | MC |
| 1 | 30 | ||||||
| 2 | 18 | ||||||
| 3 | 15 | ||||||
| 4 | 7 | ||||||
| 5 | 4 | 2 | |||||
| 3,5 | 1 |
Решение:
При Q = 5, AFC = 4, AFC = FC / Q, следовательно, FC = 5 × 4 = 20 при любом объёме выпуска.
Заполняем столбец FC полностью.
VC(1) = TC – FC = 30 – 20 = 10
АС(1) = TC / Q = 30 / 1 = 3
AVC(1) = VC / Q = 10 / 1 = 10
AFC(1) = FC / Q = 20 / 1 = 20
TC(0) = FC + VC = 20 + 0 = 20
MC(1) = (TC(1) – TC(0)) / (1 – 0) = 30 – 20 = 10
TC(2) = FC + VC = 20 + 18 = 38
АС(2) = TC / Q = 38 / 2 = 19
AVC(2) = VC / Q = 18 / 2 = 9
AFC(2) = FC / Q = 20 / 2 = 10
MC(2) = (TC(2) – TC(1)) / (2 – 1) = 38 – 30 = 8
TC(3) = AC × Q = 15 × 3 = 45
VC(3) = TC – FC = 45 – 20 = 25
AVC(3) = VC / Q = 25 / 3
AFC(3) = AC – AVC = 15 – 25/3 = 20/3
MC(3) = (TC(3) – TC(2)) / (3 – 2) = 45 – 38 = 7
VC(4) = AVC × Q = 7 × 4 = 28
TC(4) = 28 + 20 = 48
АС(4) = TC / Q = 48 / 4 = 12
AFC = AC – AVC = 12 – 7 = 5
MC(4) = (TC(4) – TC(3)) / (4 – 3) = 48 – 45 = 3
MC(5) = (TC(5) – TC(4)) / (5 – 4) = TC(5) – TC(4),
отсюда
TC(5) = MC(5) + TC(4) = 2 + 48 = 50
VC(5) = TC – FC = 50 – 20 = 30
АС(5) = TC / Q = 50 / 5 = 10
AVC(5) = AC – AFC = 10 – 4 = 6
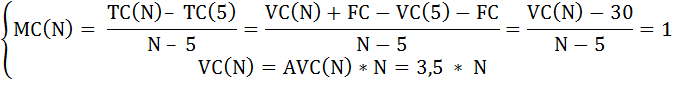
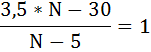
2,5 × N = 25
N = 10
VC(10) = 3,5 × 10 = 35
ТС(10) = VC + FC = 35 + 20 = 55
AC(10) = TC / Q = 55 / 10 = 5,5
AFC(10) = FC / Q = 20 / 10
Занесём полученные результаты в таблицу:
| Q | TC | VC | FC | AC | AVC | AFC | MC |
| 1 | 30 | 10 | 20 | 30 | 10 | 20 | 10 |
| 2 | 38 | 18 | 20 | 19 | 9 | 10 | 8 |
| 3 | 45 | 25 | 20 | 15 | 25/3 | 20/3 | 7 |
| 4 | 48 | 28 | 20 | 12 | 7 | 5 | 3 |
| 5 | 50 | 30 | 20 | 10 | 6 | 4 | 2 |
| 10 | 55 | 35 | 20 | 5,5 | 3,5 | 2 | 1 |
Задача 3. Расчёт цены выбора
Альтернативная стоимость
Бухгалтеру нужно покрасить свой дом. Для этого он может нанять начинающего маляра, который покрасит дом за 30 рабочих часов и просит за работу 1200 р.
Жена предлагает нашему бухгалтеру покрасить дом самому. Мотивирует она это тем, что бухгалтер в молодости был неплохим маляром. Он затратит на покраску 20 ч. И сэкономит семье деньги.
Бухгалтер завален работой и обычно зарабатывает 100 р. в час. Поэтому он отказывается сам красить дом, ссылаясь на экономическую целесообразность.
Кто прав и почему? Какова цена правильного выбора?
Решение:
Прав бухгалтер. Он сэкономит семье деньги, если будет заниматься своей работой, которая за 20 часов принесёт ему:
20 × 100 = 2000 р.
и наймёт маляра с оплатой 1 200 р.
Цена его выбора, то есть экономия при этом составит:
2 000 – 1 200 = 800 р.
Задача №4. Построение КПВ
Альтернативная стоимость
На одном поле фермер может произвести 500 т картофеля или 100 т пшеницы, а на другом альтернативная стоимость выращивания 2 т пшеницы равна 5 т картофеля при максимальном производстве картофеля, равном 1000 т. Построить кривую производственных возможностей фермера.
Решение:
Кривая производственных возможностей (КПВ) – это кривая, каждая точка которой показывает максимальные количества двух экономических благ, которые способна произвести экономика страны при полном и эффективном использовании имеющихся ресурсов и текущем уровне технологий.
Из условия задачи известно, что на первом поле фермер может произвести либо 500 т картофеля, либо 100 т пшеницы.
Для построения кривой производственных возможностей первого поля откладываем по оси ординат (пшеница) максимальное количество выращенной пшеницы, которое производилось бы в экономике, если бы все имеющиеся ресурсы были направлены на производство пшеницы, то есть 100 т. Производство картофеля в этом случае равно нулю.
И наоборот, если все имеющиеся ресурсы направлены на производство картофеля, то максимальное количество – 500 т, которое может быть произведено при полном и эффективном использовании имеющихся ресурсов, мы откладываем по оси абсцисс (картофель). Производство пшеницы в этом случае равно нулю.
Соединив две эти точки, получим КПВ первого поля.
При этом альтернативные издержки (АИ) производства 1 т картофеля – это то количество пшеницы, от выращивания которого фермер вынужден отказаться:
100 / 500 = 0,2 т пшеницы.
На втором поле фермер может произвести максимально 1000 т картофеля или 400 т пшеницы, так как альтернативная стоимость выращивания 2 т пшеницы равна 5 т картофеля. Или альтернативные издержки 1 т картофеля равны 2 / 5 = 0,4 т пшеницы.
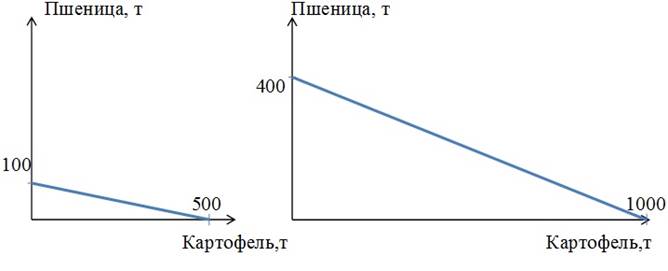
Построим суммарную КПВ для этого фермера.
Максимально возможный объём выращиваемой пшеницы – 500 тонн (на первом поле он может вырастить 100 тонн, на втором – 400 тонн). При этом объём картофеля будет нулевым. Отметим соответствующую точку на графике (точка А).
Далее определим, на каком из двух полей следует начать выращивать картофель, если фермер решит выращивать хотя бы небольшое его количество.
Для этой цели выберем из двух полей то, на котором выращивание каждой единицы картофеля приведёт к наименьшим потерям объёма пшеницы. То есть выберем то поле, где альтернативные издержки выращивания картофеля наименьшие.
На первом поле альтернативные издержки 1 т картофеля равны 0,2 т пшеницы.
А на втором поле альтернативные издержки 1 т картофеля равны 0,4 т пшеницы.
0,2 меньше чем 0,4, значит, для производства первых тонн картофеля выгоднее использовать первое поле.
Максимально на первом поле можно вырастить 500 т картофеля, пожертвовав при этом 100 тонн пшеницы.
Координаты точки перелома (точки В) – 500 тонн картофеля, 400 тонн пшеницы.
Максимальное количество картофеля, которое можно вырастить на двух полях равно 1500 тонн (500 тонн на первом поле и 1000 тонн на втором). При этом объём пшеницы будет нулевым. Обозначим точку С на оси абсцисс.
Соединив последовательно три точки А, В и С получим суммарную кривую производственных возможностей нашего фермера.

Участок земли
Рента дифференциальная, р.
Совокупная рента, R
Издержки производства включают в данной задаче расходы выращивания и транспортные расходы.
Найдём цену земли.
Субъект, желающий купить земельный участок, должен учесть альтернативные варианты вложения денег и получения дохода. Субъект выбирает: положить деньги в банк или купить земельный участок. Поэтому при всех неизменных условиях цену земли можно выразить следующей формулой:
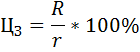
где
R – размер арендной платы (рента),
r – величина ссудного процента или процентная ставка,
Размер арендной платы = Абсолютная рента + Дифференциальная рента +
+ Процент на капитал
Так как в задании не сказано осуществлялись ли ранее капиталовложения в постройки и сооружения, размер арендной платы и размер совокупной ренты будут совпадать. В противном случае арендная плата на ряду с рентой включает в себя выплату процента на вложенный капитал и амортизационные отчисления на вложенный капитал.
Таким образом, для нашего задания:
Размер арендной платы = Абсолютная рента + Дифференциальная рента =
= Совокупная рента
Абсолютная рента получается собственниками земли абсолютно со всех земельных участков и абсолютно одинаковой величины, если размеры земельных участков одинаковы.
В условии задания сказано, что все четыре участка одинаковы по площади и величина абсолютной ренты равна 300 р.
Дифференциальная рента будет получена собственниками земли только со средних и лучших участков земли, как по качеству и плодородию почвы, так и по месторасположению. Участки, обладающие дифференциальной рентой: I, II и III.
IV участок земли будет иметь только абсолютную ренту. Поэтому виды ренты будут способствовать формированию цен на землю. Цена земли IV участка будет зависеть только от величины абсолютной ренты и величины ссудного капитала, в отличии от I, II и III участка, где цена зависит ещё и от величины дифференциальной ренты.
Совокупная рента - это избыточная прибыль которую присваивают собственники земли.
Можно сказать, что собственник III участка, за счёт наилучшей его производительности получит наибольшую избыточную прибыль.
Рассчитаем цены земельных участков.
Цена I участка земли:
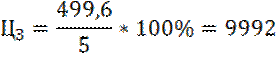
Цена II участка земли:
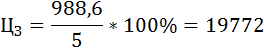
Цена III участка земли:
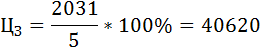 .
.
Цена VI участка земли:
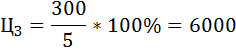
Проект
Доходы
Всего доходы
Рассчитать, какой проект является наиболее выгодным для инвестирования.
Решение:
Для оценки будущих доходов при альтернативных вложениях капитала найдём текущую дисконтированную стоимость для каждого проекта по формуле:
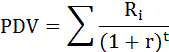
где
PDV – текущая дисконтированная приведённая стоимость,
Ri – доход от инвестиций в году t,
r – ставка процента.
Величина дисконтированного дохода проекта Зайка:
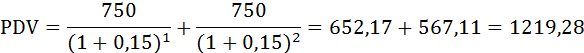
Величина дисконтированного дохода проекта Белочка:
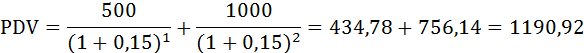
Величина дисконтированного дохода проекта Енотик:
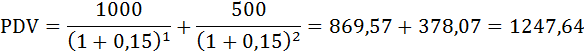
Итак, проект Енотик оказывается предпочтительнее для инвестирования
Задача 9.
Спрос и предложение на обеды в студенческой столовой описываются уравнениями: QD = 2400 – 100P; QS = 1000 + 250P, где Q – кол-во обедов в день, Р – цена обеда (ден. ед.). Вычислите равновесную цену и кол-во проданных обедов по такой цене. Заботясь о студентах, администрация установила цену в 3 ден. ед. за обед. Охарактеризуйте последствия такого решения.
Дано:
QD=2400-100P
QS=1000+250P
P1=3 ден. ед.
Найти: Pe-? Qe-?
Решение:
В состоянии равновесия объем спроса равен объему предложения
2400-100P=1000+250P
1400=350P
P=4 ден. ед. (равновесная цена)
Qe=2400-100P=2000 обедов (равновесный объем)
Р1=3 ден. ед., тогда QD=2400-100*3=2100 обедов
QS=1000+250*3=1750 обедов
Таким образом, при цене обеда 3 ден. ед. наблюдается дефицит, составляющий 350 обедов.
Задача 10.
В набор потребителя входят два товара: минеральная вода и печенье. Предельная полезность характеризуется следующими данными:
| Количество минеральной воды | 1 | 2 | 3 | 4 | 5 | 6 |
| Предельная полезность (MU) | 10 | 8 | 6 | 4 | 3 | 2 |
| Количество печенья | 1 | 2 | 3 | 4 | 5 | 6 |
| Предельная полезность (MU) | 7 | 6 | 5 | 4 | 3 | 2 |
Цена одной бутылки минеральной воды 10ден. ед., цена одной пачки печенья – 5ден. ед.. Общий доход потребителя, который он тратит на минеральную воду и печенье, равен 25ден. ед. Какое количество минеральной воды и печенья покупает рациональный потребитель?
Дано:
Рх=10ден. ед.
Ру=5ден. ед.
I=25ден. ед.
Найти: рациональный выбор.
Решение:
Потребителький выбор – это выбор, максимизирующий функцию полезности рационального потребителя в условиях ограниченности ресурсов (денежного дохода). Функция полезности максимизируется в том случае, когда денежный доход распределяется таким обоазом, что последняя денежная единица (рубль, евро и т. д), затраченная на приобретение любого блага, приносит одинаковую предельную полезность.
Равновесие потребителя соответствует след. условию:
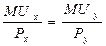
Рассчитаем значение предельно полезности на одну ден. ед.
| Кол-во мин. воды | Преде-я полезн-ть мин. воды на 1 ден. ед | Кол-во печенья | Преде-я полезн-ть печенья на 1 ден. ед |
| 1 | 1 | 1 | 1,4 |
| 2 | 0,8 | 2 | 1,2 |
| 3 | 0,6 | 3 | 1 |
| 4 | 0,4 | 4 | 0,8 |
| 5 | 0,3 | 5 | 0,6 |
| 6 | 0,2 | 6 | 0,4 |
Этому равенству соответствует несколько комбинаций: 1 бутылка мин. воды и 3 пачки печенья; 2 бутылки мин. воды и 4 пачеи печенья; 3 бутылки минеральной воды и 5 пачек печенья; 4 бутылки минеральной воды и 6 пачек печенья, но только одна комбинация входит в бюджет потребителя, а другие выходят за рамки данного бюджета.
С учетом бюджетного ограничения:
I=Px*Qx+Py*Qy
25=10*1+5*3
10+15=25
Ответ. Рациональный потребитель покупает 1 бутылку минеральной воды и 3 пачки печенья.
Задача 11.
В краткоср-м периоде фирма может варьировать исп-е труд-х ресурсов, но не может повлиять на вел-ну исп-го капитала. Таблица показывает, как изм-ся выпуск пр-и вследствие изм-я объемов применяемого труда.
| Затраты труда (чел./нед.) | Объем продукта (ед./нед.) | MPL | APL |
| 1 | 35 | 35 | 35 |
| 2 | 80 | 45 | 40 |
| 3 | 122 | 42 | 41 |
| 4 | 156 | 34 | 39 |
| 5 | 177 | 21 | 35,4 |
| 6 | 180 | 3 | 30 |
Опр-те, при каких затратах труд будет исп-ся с максимальной эффективностью.
Решение:
MPL = ΔTP/ΔF
MPL1 = (35-0)/(1-0)=35 ед.
MPL2 = (80-35)/(2-1)=45 ед.
MPL3 = (122-80)/(3-2)=42 ед.
MPL4 = (156-122)/(4-3)=34 ед.
MPL5 = (177-156)/(5-4)=21 ед.
MPL6 = (180-177)/(6-5)=3ед.
APL = TP/F
APL1 = 35/1=35 APL2 = 80/2=40
APL3 = 122/3=41 APL4 = 156/4=39
APL5 = 177/5=35,4 APL6 = 180/6=30
Т. о., труд будет исп. ся с максимальной эф. тью при затратах 2 чел. ка, т. к. предельный продукт имеет максимальное значение.
Задача 12.
Используя данные таблицы о затратах труда (L), капитала (K) и объеме выпуска (Q), определите характер экономии от масштаба при переходе от А к Б, от Б к В и от В к Г. Решение А: затраты факторов пр-ва: 40+20=60 ед. Q=200 ед. Б: затраты факторов пр-ва: 60+30=90 ед. Q=400 ед. Δ50% Δ100% При переходе от А к Б набл-ся возрастающая экономия от масштаба. т. к. ув-е затрат факторов пр-ва на 50% привело к росту объема выпуска продукции на 100%. Б: 60+30=90 ед. Q=400 ед. В: 120+60=180 ед. Q=800 ед. Δ100% Δ100% При переходе от Б к В набл-ся постоянная экономия от масштаба. В: 120+60=180 ед. Q=800 ед. Г: 180+90=270 ед. Q=880 ед. Δ50% Δ10% При переходе от В к Г наблюдаем убывающую экономию от масштаба. Ответ: Оптимальный размер предприятия достигнут в точке В, после которого приращение пр-ва достигается за счет непропорционально больших задач. Задача 13 Фирма планирует выпустить учебник. Средние совокупные издержки на производство книги описываются уравнением: ATC=4+4000/Q, где Q-количество учебников, выпущенных за год. Планируемая цена учебника 8 ден. ед. Каков должен быть годовой тираж учебника, соответствующий точке безубыточности? Дано: АТС=4+4000/Q Р=8 ден. ед. Найти: Q-? Решение: По условию самоокупаемости(безубыточности) средние общие издержки равны значению цены АТС=Р 4+4000/Q=8 Q=1000 учебников. Ответ: годовой тираж учебника, соответствующий точке безубыточности, составит 1000 экземпляров. Задача 14 В таблице содержаться данные об издержках Фирсы, работающей на рынке совершенной конкуренции Используя данную инф-ю, выполните след-е задания: 1.Рассчитайте значения общих издержек, предельных издержек, средних общих издержек, средних переменных издержек для каждого значения Q 2.Используя предельный подход, определите, будет ли данная фирма производить в краткосрочном периоде, если цена товара составит 32 ден. ед. если фирма производит, то каков будет бъем пр-ва, максимизирующий прибыль или минимизирующий убыток? Решение 1.Рассчитаем издержки фирмы для каждого значения Q - общие изд. TC = FC+VC - предельные издержки MC =∆TC/∆Q - средние общие издержкиATC = TC/Q - средние переменные издержки AVC=VC/Q 2. При условии, что цена превышает минимум средних переменных издержек (AVC), конкурентная фирма будет максимизировать прибыль или минимизировать убытки в краткосрочном периоде, производя такой объем продукции, при котором цена равна предельным издержкам Ответ: фирма выходит из отрасли, так как цена меньше значения средних переменных издержек для любого количества товара. Задача 15. Определите общую денежную выручку, коэффициент эластичности спроса и тип эластичности, заполнив соответствующие строчки в таблице: Показ-ли Товар - Х Товар - У Неэластичный Эластичный Решение: Рассчитаем выручку производителя TR=P*Q Для товара Х TRxo=4*10=40 тыс. д.ед. TRx1= 3*12=36 тыс. д.ед. Для товара У ТRyo= 10*1=10 млн. д.ед ТRy1= 5*3=15 млн. д.ед. Q1 – первоначальный объем спроса Q – изменившийся объем спроса P – первоначальная цена P – изменившаяся цена Для товара Х Для товара У Ответ: спрос на товар Х является неэластичным, так как значение коэффициента эластичности по модулю больше единицы. Задача 1. Расчёт затрат Производство и затраты фирмы Заполните таблицу на основании следующих данных о затратах фирмы в краткосрочном периоде: Решение: Расшифровка обозначений, определения и формулы подробно рассмотрены в задаче №71. Начнём заполнение таблицы с нахождения общих издержек при Q = 1: АС(1) = TC(1) / Q = 8 Отсюда: TC(1) = 8 TC(2) = TC(1) + MC(2) = 8 + 4 = 12 FC = AFC × Q = 2 × 3 = 6 для любого Q. Заполним первый столбец: AFC(1) = 6 / 1 = 6 AFC(2) = 6 / 2 =3 AFC(4) = 6 / 4 =1,5 При Q = 0 TC(0) = FC = 6 MC(1) = TC(1) - TC(0) = 8 - 6 = 2 AC(2) = TC(2) / 2 = 12 / 2 = 6 AC(3) = TC(3) / 3 = 15 / 3 = 5 MC(3) = TC(3) - TC(2) = 15 - 12 = 3 TC(4) = FC + VC(4) = 6 + 11 = 17 MC(4) = TC(4) - TC(3) = 17 - 15 = 2 AC(4) = TC(4) / 4 = 17 / 4 = 4,25 Осталось заполнить столбец переменных издержек: VC(0) = 0 VC(1) = TC(1) - FC = 8 - 6 = 2 VC(2) = TC(2) - FC = 12 - 6 = 6 VC(3) = TC(3) - FC = 15 - 6 = 9 Заполним таблицу: Задача 2. Расчёт издержек фирмы Производство и затраты фирмы Информация о деятельности фирмы, кроме представленной в таблице, оказалась утраченной. Восстановите недостающую информацию об издержках фирмы. Решение: При Q = 5, AFC = 4, AFC = FC / Q, следовательно, FC = 5 × 4 = 20 при любом объёме выпуска. Заполняем столбец FC полностью. VC(1) = TC – FC = 30 – 20 = 10 АС(1) = TC / Q = 30 / 1 = 3 AVC(1) = VC / Q = 10 / 1 = 10 AFC(1) = FC / Q = 20 / 1 = 20 TC(0) = FC + VC = 20 + 0 = 20 MC(1) = (TC(1) – TC(0)) / (1 – 0) = 30 – 20 = 10 TC(2) = FC + VC = 20 + 18 = 38 АС(2) = TC / Q = 38 / 2 = 19 AVC(2) = VC / Q = 18 / 2 = 9 AFC(2) = FC / Q = 20 / 2 = 10 MC(2) = (TC(2) – TC(1)) / (2 – 1) = 38 – 30 = 8 TC(3) = AC × Q = 15 × 3 = 45 VC(3) = TC – FC = 45 – 20 = 25 AVC(3) = VC / Q = 25 / 3 AFC(3) = AC – AVC = 15 – 25/3 = 20/3 MC(3) = (TC(3) – TC(2)) / (3 – 2) = 45 – 38 = 7 VC(4) = AVC × Q = 7 × 4 = 28 TC(4) = 28 + 20 = 48 АС(4) = TC / Q = 48 / 4 = 12 AFC = AC – AVC = 12 – 7 = 5 MC(4) = (TC(4) – TC(3)) / (4 – 3) = 48 – 45 = 3 MC(5) = (TC(5) – TC(4)) / (5 – 4) = TC(5) – TC(4), отсюда TC(5) = MC(5) + TC(4) = 2 + 48 = 50 VC(5) = TC – FC = 50 – 20 = 30 АС(5) = TC / Q = 50 / 5 = 10 AVC(5) = AC – AFC = 10 – 4 = 6 2,5 × N = 25 N = 10 VC(10) = 3,5 × 10 = 35 ТС(10) = VC + FC = 35 + 20 = 55 AC(10) = TC / Q = 55 / 10 = 5,5 AFC(10) = FC / Q = 20 / 10 Занесём полученные результаты в таблицу:
L, чел.
К, ед.
Q, ед.
А
40
20
200
Б
60
30
400
В
120
60
800
Г
180
90
880
Общее кол-во продукта Q, ед
Пост-е изд-ки, д. е
(FC)
Прем-е изд-ки д. е
(VC)
Общие изд-ки (ТС),д. е
Пред-е изд-ки(МС)д. е
Ср-е общ. изд-ки(АТС) ден. ед
Ср-е переем. изд-ки (AVC)
1
60
45
105
-
105
45
2
60
91
151
46
755
45
3
60
120
180
29
60
40
4
60
150
210
30
525
37.5
5
60
185
245
35
49
37
6
60
225
285
40
475
37.5
7
60
270
330
45
47.14
38.57
8
60
325
385
55
4813
4063
9
60
390
450
65
50
43.33
10
60
465
525
75
525
46.5
Первонач-е знач-ие
Изм-ся значение
Первонач-е знач-ие
Изм-ся значение
1. Цена (Р), ден. ед.
4 тыс.
3 тыс.
10 млн.
5 млн.
2. Кол-во (Q), шт.
10
12
1
3
3. Выручка (TR), ден. ед.
40 тыс.
36 тыс.
10 млн.
15 млн.
4.Коэф-ент эластичности Edr
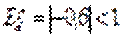
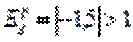
5. Тип эластичности
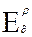 =
= 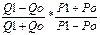 , где
, где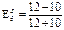 *
* 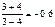
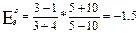
Q
AFC
VC
AC
MC
TC
0
1
8
2
4
3
2
15
4
11
Q
AFC
VC
AC
MC
TC
0
-
0
-
-
6
1
6
2
8
2
8
2
3
6
6
4
12
3
2
9
5
3
15
4
1,5
11
4,25
2
17
Q
TC
VC
FC
AC
AVC
AFC
MC
1
30
2
18
3
15
4
7
5
4
2
3,5
1
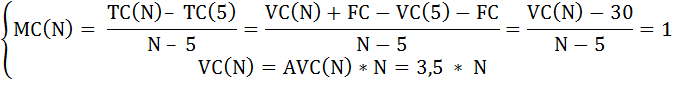
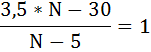
Q
TC
VC
FC
AC
AVC
AFC
MC
1
30
10
20
30
10
20
10
2
38
18
20
19
9
10
8
3
45
25
20
15
25/3
20/3
7
4
48
28
20
12
7
5
3
5
50
30
20
10
6
4
2
10
55
35
20
5,5
3,5
2
1
Дата: 2019-02-19, просмотров: 1112.