Чувствительность к тепловому импульсу без пламени чаще всего характеризуется температурой вспышки. Практически температуру вспышки ЭКМ определяют как наименьшую температуру, до которой надо нагреть взрывчатое вещество для того, чтобы вызвать в нем химические превращение со скоростью, достаточной для получения звукового эффекта и пламени.
Температура вспышки не является строго постоянной для каждого вещества, а зависит от ряда причин, в первую очередь от условий, определяющих соотношение между теплоприходом и теплоотводом. Она зависит:
а) от температуры источника тепла, следовательно, от температуры испытуемого ЭКМ (чем меньше эта температура, тем ниже температура вспышки);
б) от величины навески; при уменьшении величины навески увеличивается температура вспышки, а, начиная с некоторой навески, разложение вещества произойдет без вспышки (теплоприход пропорционален объему, а теплоотвод – поверхности).
Чтобы получить сравнимые результаты, температуру вспышки или самовоспламенения, (т. е. воспламенение без поджигания) определяют в строго определенных условиях.
Опытное определение температуры вспышки . В специальной железной бане расплавляют легкоплавкий металлический сплав. По достижении заданной температуры, близкой к ожидаемой температуре вспышки, в баню погружают стеклянную или металлическую пробирку с навеской массы в 0,1 г пороха или 0.05 г бризантного ЭКМ. Отмечают продолжительность выдержки до момента вспышки при этой температуре. Повторными опытами определяют с точностью до 5°С минимальную температуру, ниже которой при выдержке в 5 секунд или 5 минут вспышки не наблюдается.
Температура вспышки не характеризует воспламеняемость ЭКМ, а лишь температурную устойчивость ЭКМ к нагреву и относительную химическую стойкость вещества, если речь идет о веществах одной природы. Температура вспышки нитроцеллюлозных порохов определяется термической стойкостью нитроцеллюлозы и нитроэфира. Так как температура интенсивного разложения компонентов СТРТ: связующих каучуков и ПХА находится на уровне 200…3000С, то и температура вспышки СРТТ составляет 200…3000С.
Пороха и топлива по чувствительности к тепловому импульсу можно расположить в ряд: ПП > БП > СТРТ > ДРП > ВВ.
Температуры вспышки важнейших ЭКМ приведены в табл. 18.
Температура вспышки ЭКМ. Таблица 18.
| Взрывчатое вещество | Твсп,ОС при τзад=5сек | Твсп,ОС при τзад=300сек |
| Пироксилин | − | 185…195 |
| Нитроглицерин | 220 | 210 |
| Бездымные пороха | 270 | 180…220 |
| Дымный порох | − | 290…310 |
| Тротил | 475 | 290…295 |
| Аммониты | − | 220…240 |
| Гексоген | − | 230 |
| СТРТ (на основе ПХА и инертного связующего) | 250…350 | 200…300 |
Температура вспышки является одним из основных показателей, по которым определяется пожароопасиость ЭКМ.
Для расчета критических параметров теплового взрыва зарядов РДТТ в настоящее время используется следующий алгоритм. Критическими параметрами называют наименьшую температуру заряда Ткр, при которой возможно его тепловое самовоспламенение, и время до воспламенения τкр.
В качестве математической модели процесса теплового самовоспламенения используют уравнение теплового баланса:
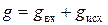 , (5)
, (5)
где g – количество тепла, накапливающееся в локальной области исследуемой системы, 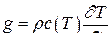 ;
;
gвх – количество тепла, образующееся в данной локальной области исследуемой системы за счет экзотермических реакций разложения, 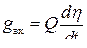 ;
;
gисх – дивергенция (расходимость) вектора потока тепла, обусловленная взаимодействием данной локальной области с окружающими локальными областями системы и окружающей средой, 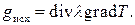
Поскольку заряды, как правило, имеют форму цилиндра, уравнение теплопроводности для одномерного потока тепла в заряде удобно представить в цилиндрических координатах как:
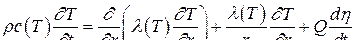 (6)
(6)
Таким образом, математическая модель процесса теплового самовоспламенения (системообразующее отношение) представляет собой дифференциальное уравнение в частных производных второго порядка параболического типа, где Q – тепловой эффект термического разложения; η – глубина термического разложения (0 < η < 1); dη/dt – скорость реакции термического разложения; c(T) – теплоемкость; λ(T) – коэффициент теплопроводности; ρ – плотность топлива.
Любое из дифференциальных уравнений переноса, которое мы хотим использовать в качестве модели, является математической моделью целого класса явлений, т.е. оно в математической форме отражает всю совокупность явлений, характеризуемых одинаковым механизмом процессов. Чтобы получить из множества возможных решений данного уравнения одно частное решение, надо знать все конкретные особенности данного явления.
Конкретное явление характеризуется следующими индивидуальными признаками, выделяющими его из целого класса явлений.
1. Любая рассматриваемая система имеет определенные размеры и форму, поэтому в условия однозначности обязательно должны входить геометрические свойства системы (параметр формы, размеры).
2. Тела, составляющие данную систему, обладают определенными физическими свойствами. Поэтому для определения данного явления необходимо задать все физические свойства тел, существенные для данного процесса: Q, h, dh/dt, c(T), λ(T), ρ.
Дата: 2019-02-19, просмотров: 720.