Телемеханики
При управлении производственным процессом происходит по-
стоянный обмен различными сообщениями о событиях, происходя-
щих в той или иной точке процесса. Эти сообщения несут информа-
цию о его состояниях (значении контролируемого параметра, со-
стоянии исполнительного механизма, уставке регулятора) или
предназначены для изменения этих состояний (команды управле-
ния) — например, сообщение об изменении давления в трубопрово-
де или команда на закрытие задвижки.
Для получателя сообщения, как правило, интерес представляет
только его новая часть — информация, т. е. содержательные сведения
(данные), ранее ему неизвестные.
Сообщения передаются с помощью сигналов. Сигналом называ-
ется носитель (переносчик) сообщения. Таким средством могут слу-
жить любые физические явления или объекты, изменение параметров
которых во времени несет информацию в прямом или закодирован-
ном виде (свет, звук, напряжение, ток, давление и т.д.). Наибольшее
распространение получили электрические сигналы. Сигнал должен
однозначно отображать сообщение, а после преобразований восста-
навливаться без потери информации.
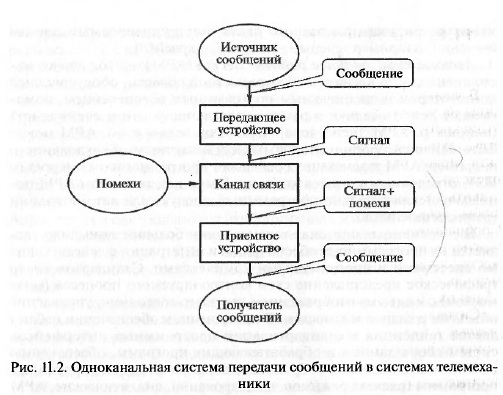
Процесс передачи сообщений условно показан в виде схемы, по-
казанной на рис. 11.2. Сообщение от источника поступает в передаю-
щее устройство, которое преобразует его в сигнал, передаваемый по
каналу связи. Процесс автоматического преобразования в сигнал,
происходящий в передающем устройстве, включает в себя одну или
несколько из следующих операций: преобразование из одной физи-
ческой формы в другую, квантование, модуляцию, кодирование.
Канал связи начинается на входе передающего устройства и конча-
ется на выходе приемного устройства. В процессе передачи на сигнал
накладываются различные помехи. Приемное устройство отфильтро-
вывает их и восстанавливает по полученному сигналу сообщение для
получателя.
11.3. Преобразование сообщений для передачи
По каналам связи
В зависимости от характера изменения во времени сообщения де-
лятся на четыре группы: 1) непрерывные; 2) дискретные по времени;
3) дискретные по множеству; 4) дискретные по времени и по множе-
ству. Технологические параметры, характеризующие состояние объ-
екта управления (температура, давление, уровень, скорость и т.д.),
представляют собой непрерывные сообщения, которые можно пред-
ставить в виде функции X(t), причем эта функция может принимать
любые вещественные значения в диапазоне изменения аргумента t.
Сообщения, которые могут изменяться в строго определенные мо-
менты, называются дискретными по времени. Дискретные по мно-
жеству сообщения имеют ограниченное количество значений, напри-
мер: состояние крана — открыт или закрыт. Существуют также со-
общения, дискретные как по времени, так и по множеству.
Сигналы также делятся на непрерывные и дискретные. Непре-
рывный по времени сигнал — это сигнал, определенный для любого
момента времени, т.е. он также представляет собой непрерывную
функцию. Дискретные по времени сигналы — это сигналы, опреде-
ленные только в дискретные моменты времени, например через
каждую секунду.
Любое непрерывное сообщение может быть с достаточной точно-
стью передано дискретными сигналами. Процесс замены непрерыв-
ного сообщения дискретным называется квантованием. Если сообще-
ние меняется на дискретное по множеству, квантование называется
квантованием по уровню, а если на дискретное по времени — кванто-
ванием по времени.
При квантовании по уровню значение функции X(t) в произволь-
ный момент времени заменяется своим ближайшим значением, на-
зываемым уровнем квантования. Интервал между двумя соседними
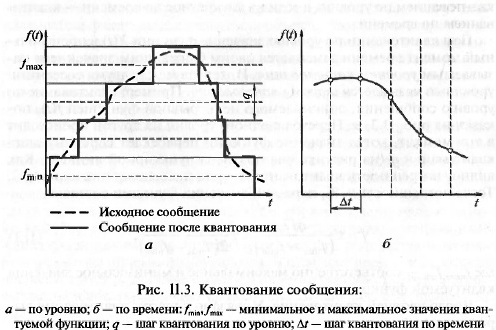
уровнями называется шагом квантования. Пример: квантование по
уровню сообщения, описываемого непрерывной функцией ƒ(t), по-
казан на рис. 11.3, а. Переход с одного уровня на другой происходит
в тот момент, когда значение функции пересекает середину шага
квантования q (на рисунке она показана пунктирной линией). Как
видно, погрешность квантования ∆шах не превышает значения q/ 2.
Тогда погрешность γ, %, передачи значений функции составит
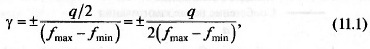
Где ƒmax,ƒmin— соответственно максимальное и минимальное значения
квантуемой функции.
Число уровней квантования N связано с шагом квантования вы-
Ражением
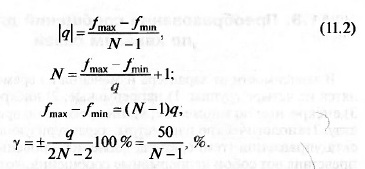
На практике, как правило, решается задача определения необходи-
мого числа N исходя из заданной точности передачи, т.е. значения у.
При квантовании по в р е м е н и значения функции передаются
в определенные моменты времени независимо от того, изменилось
ее значение или нет. Необходимость такой передачи объясняется не-
сколькими причинами: во-первых, за малое время значение сообще-
ния может изменяться очень незначительно; во-вторых, обработка
сообщений получателем производится последовательно во времени;
в-третьих, передача сообщений только в фиксированные моменты
сокращает объем передаваемой и обрабатываемой информации. При-
мер квантования по времени сообщения, описываемого непрерывной
функцией f{t), показан на рис. 11.3, б. Как видно из рисунка, кван-
тованное сообщение представляется в виде отдельных отсчетов функ-
ции Д/), получаемых в моменты времени кх, к= 1, 2, .. При получе-
нии проквантованного по времени сообщения возникает задача
восстановления значений исходного сообщения в произвольные
моменты, не равные кх, к = 1, 2,.... Это возможно в том случае, если
дискретные отсчеты разделены интервалом

где ,F mix — максимальная частота изменения исходной функции (след-
ствие теоремы Котельникова).
Для передачи полученных в результате квантования дискретных
значений, как правило, используются сигналы постоянного (видеоим-
пульсы) или переменного (радиоимпульсы) тока. Видеоимпульсы могут
быть различной формы: прямоугольные, треугольные, синусоидальные,
трапецеидальные, экспоненциальные и др. Радиоимпульсы образуются
наполнением видеоимпульсов высокочастотными гармоническими
колебаниями. Сообщение в этом случае представляется изменением
одного или нескольких параметров сигнала, например: амплитуды,
частоты, фазы и т. п. Этот процесс наложения сообщения на перенос-
чик информации называется модуляцией. Основной смысл модуля-
ции — передача низкочастотного сообщения высокочастотным сигна-
лом, который обеспечивает следующие преимущества: значительное
уменьшение мощности передатчика и затухания сигнала; возможность
одновременной передачи по одной линии связи разных сообщений;
повышение достоверности передаваемых сообщений вследствие лучшей
помехозащищенности модулированных сигналов. В зависимости от
того, какой параметр переносчика меняется, модуляция может быть
непрерывной (амплитудной, частотной, фазовой) или импульсной
(широтно-импульсной и т. д.). А сами параметры сигнала, используемые
дая передачи, называются импульсными признаками. К ним относятся:
1) полярность — этот признак является наиболее помехозащищенным,
но позволяет формировать только два различных состояния; 2) ампли-
туда импульса — с помощью этого признака можно сформировать
любое число состояний, но амплитуда сигнала наиболее подвержена
действию помех; кроме того, если амплитуды соседних сигналов от-
личаются незначительно, их трудно различать на приемной стороне;
3) длительность импульса; 4) частота импульсов; 5) фаза импульса — с
помощью этого признака обычно тоже формируется только два со-
стояния, одному из которых соответствует посылка импульса, синфаз-
ного опорному сигналу, а другому сообщению — импульса, находяще-
гося в противофазе с опорным сигналом. Наиболее часто используют-
ся полярность импульса (при передаче на постоянном токе) и частота
импульсов (при передаче на переменном токе).
Кодирование сообщений
Кодирование, — это преобразование по определенному правилу
дискретного сообщения в дискретный сигнал в виде кодовых комби-
наций. Обратный процесс (декодирование) должен однозначно вос-
становить передаваемое сообщение. Целью кодирования является
эффективное использование каналов связи и увеличение достовер-
ности передачи информации.
Код (от лат. codex — свод законов) — система условных знаков,
символов для передачи, обработки и хранения различнбй информа-
ции. Конечная последовательность кодовых знаков называется кодо-
вым словом. Число различных символов, которые используются в
словах кода, называется основанием т данного кода, а сами символы
составляют так называемый кодовый алфавит. Число элементов кода
в кодовом слове определяет его длину, или разрядность, п. Код на-
зывается равномерным, если все кодовые комбинации одинаковы по
длине, и неравномерным, если значение п в коде непостоянно. Место
элемента в кодовом слове определяет его разряд. Число кодовых
комбинаций N, которые можно образовать в коде, называется объ-
емом кода. Характеристики кода связаны между собой зависимостью
N - т". Например, в коде Морзе применяются два символа: точка и
тире. Следовательно, такой код является двоичным (т = 2). Все бук-
вы русского алфавита кодируются с помощью кодовых слов (кодовых
комбинаций) различной длины, поэтому код Морзе — неравномер-
ный двоичный.
В любой системе счисления числа представляются в виде набора
коэффициентов перед числом, которое является основанием системы
счисления и имеет определенную степень. Обычная система счисле-
ния, используемая людьми при счете, — десятичная, т.е. кодовый
алфавит содержит 10 символов — от 0 до 9.
При передаче сообщений наиболее широкое распространение
получили двоичные коды ( т = 2), использующие символы 0 и 1. Это
объясняется простотой технической реализации такого кодирования,
так как большинство элементов автоматики имеет два взаимоисклю-
чающих состояния (контакт реле замкнут или разомкнут, транзистор
открыт или закрыт). При использовании двоичных кодов кодируемые
сообщения записываются в двоичной системе счисления, т.е. пред-
ставляются в виде набора коэффициентов 1 и 0 перед числом 2 в
соответствующей степени. Например, число 6 в двоичной системе
будет иметь вид 110:6 -> 1*22 + 1*21+0*20->110
Если десятичное число просто переводится в двоичную систему,
то полученные кодовые комбинации образуют натуральный двоич-
ный код (НДК), или двоичный код на все сочетания. Это самый
простой код, представляющий собой равномерный код длины п. В нем
для отражения значений сообщения используются все возможные ко-
довые комбинации, отличающиеся друг от друга хотя бы одним элемен-
том в каком-нибудь разряде. Число таких комбинаций N= 2".
Ниже в качестве примера представлена запись чисел от 0 до 9
четырехразрядным двоичным кодом.

Двоично-десятичный код позволяет записать каждый разряд деся-
тичного числа в виде четырехразрядного двоичного кода, т. е. в двоич-
ной системе счисления представляется отдельно каждая цифра. Напри-
мер, число 8 247 запишется в виде 1000 0010 0100 0111 (8->1000,
2->0010, 4->0100, 7->0111).
В рассмотренных кодах все возможные кодовые комбинации ис-
пользуются для передачи информации. Такие коды являются про-
стыми, или кодами без избыточности, и относятся к так называемым
непомехозащищенным кодам. Это коды, в которых имеются хотя бы
две разрешенные (т. е. используемые для передачи сообщений) кодо-
вые комбинации, переходящие одна в другую при замене в какой-
нибудь из них кодового символа другим. При этом искажение любо-
го разряда под действием помехи не может быть обнаружено, так как
приводит к возникновению другой разрешенной кодовой комбина-
ции. Например, если среди используемых кодовых комбинаций дво-
ичного трехразрядного кода имеются комбинации 110 и 010, код будет
непомехозащищенным, так как замена 1 на 0 в старшем разряде пер-
вой комбинации превратит ее во вторую. Помехозащищенными
(корректирующими) называются коды, позволяющие только обнару-
жить или обнаружить и исправить ошибки, возникающие в кодовых
комбинациях. Корректирующие коды строятся так, что для передачи
сообщения используются не все кодовые комбинации, которые мож-
но образовать посредством данного кода, а лишь некоторая их часть
(так называемые разрешенные кодовые комбинации). Тем самым
создается возможность обнаружения и исправления ошибки при не-
правильном воспроизведении некоторого числа символов. Коррек-
тирующие свойства кодов достигаются введением в кодовые комби-
нации дополнительных (избыточных) символов.
Для иллюстрации помехозащитных свойств удобно использовать
геометрическую модель кода (модель Хемминга). В соответствии с
этой моделью любой «-разрядный код представляется я-мерным
многогранником, в вершинах которого располагаются все разрешен-
ные кодовые комбинации. Соседние кодовые комбинации, имеющие
общее ребро, отличаются только в одном разряде. Расстояние между
произвольными кодовыми комбинациями, измеряемое минимальным
числом ребер между ними, называется кодовым расстоянием d. Ис-
пользуя геометрическую модель Хэмминга, можно определить связь
между кодовым расстоянием и числом обнаруживаемых (г) и исправ-
ляемых (5) ошибок. На рис. 11.4 показана модель Хэмминга для трех-
разрядного натурального двоичного кода. Все его возможные комби-
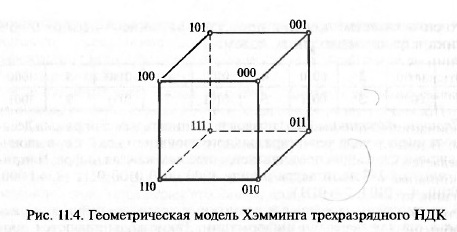
нации размещены в вершинах трехмерного куба. Действие помехи
проявляется в том, что вместо любого символа 1 может появиться
символ 0 и наоборот. Пусть один из символов какой-нибудь комби-
нации заменен другим. Если при кодировании используются все
кодовые комбинации, то переданный сигнал трансформируется в
другой и код будет непомехозащищенным. Если же требуется обна-
ружить одну ошибку, то необходимо, чтобы точки, изображающие
различные сообщения, не имели общих ребер. Этому условию удо-
влетворяют только четыре точки, расположенные по диагонали гра-
ней, например: 001, 100, 010, 111, для которых d = 2. Изменение
одного из символов этих комбинаций переводит точку в положение,
не соответствующее ни одной из выбранных четырех кодовых ком-
бинаций, и ошибка, таким образом, обнаруживается. Если же требу-
ется, чтобы одиночная ошибка была не только обнаружена, но и
исправлена, выбранные комбинации должны отличаться в трех раз-
рядах (d = 3), т.е. должны располагаться по диагонали куба (например,
000 и 111); все остальные комбинации являются запрещенными. Ми-
нимальное кодовое расстояние (наименьшее расстояние между каждой
парой комбинаций, используемых в коде) связано с корректирующи-
ми свойствами кода соотношением d = r + s+ 1. Таким образом, для
придания кодам помехозащитных свойств необходимо увеличить
кодовое расстояние. Это можно сделать двумя способами: 1) исполь-
зование не всех комбинаций кода на все сочетания; 2) добавление к
комбинации НДК определенного количества контрольных разрядов
по определенному правилу. На практике, как уже отмечалось, обыч-
но используется второй способ.
Коды, позволяющие обнаружить ошибку, называются обнаружи-
вающими. Коды, позволяющие обнаружить и исправить ошибки,
называются корректирующими. Простейшим кодом, позволяющим
обнаружить все ошибки нечетной (четной) кратности, является код
с проверкой на четность (нечетность). Этот код используется, на-
пример, для обеспечения достоверности ТИ и ТС. Он образуется
добавлением к каждой кодовой комбинации еще одного контроль-
ного символа. При защите на четность добавляется 1, если число
единиц в основной кодовой комбинации нечетное, 0 — если число
единиц четное. При приеме кодовых комбинаций этого кода под-
считывается число единиц в них. Если оно оказывается четным, это
означает, что одиночной ошибки или ошибки нечетной кратности
нет. Поскольку одиночная ошибка наиболее вероятна, принятую
комбинацию с большой долей достоверности можно считать правиль-
ной. В ней отбрасывается последний контрольный символ и она
передается получателю. Если же число единиц в принятой кодовой
комбинации нечетное, это означает, что при передаче кодовой ком-
бинации произошла одиночная ошибка (или ошибка нечетной крат-
ности). В этом случае требуется повторить передачу этой кодовой
комбинации. При защите на нечетность проверка производится по
противоположному критерию; такой код обнаруживает ошибки чет-
ной кратности. Для защиты команд ТУ, как уже упоминалось, ис-
пользуется инверсный код. Он строится из НДК следующим образом:
если в исходной комбинации четное число единиц, то добавляет-
ся еще такая же комбинация; если же число единиц нечетное, то
добавляется комбинация, инверсно повторяющая исходную:
ОНО—>01100110; 0100^-01001011. Декодирование происходит в соот-
ветствии со следующим алгоритмом: 1) анализируется информаци-
онная часть поступившего инверсного кода; 2) если число единиц в
ней четное, то контрольная часть сохраняется неизменной, если не-
четное, контрольная часть инвертируется; 3) осуществляется побит-
ное сравнение информационной и контрольной частей; 4) если все
разряды совпадают, то принимается решение о правильном приеме,
контрольная часть отбрасывается, а информационная используется
по назначению; 5) если хотя бы один разряд не совпадает, принима-
ется решение о неправильном приеме и кодовая комбинация браку-
ется.
Оба рассмотренных кода относятся к обнаруживающим, исправ-
лять ошибки они не могут.
Технические устройства для преобразования сообщений в код и
обратно называют по-разному: кодовые преобразователи, шифрато-
ры/дешифраторы, кодеры/декодеры. Простейшими устройствами
этого семейства являются так называемые кодовые маски. Кодовая
маска — это устройство, используемое в преобразователях угловых и
линейных перемещений для преобразования последних в код. В за-
висимости от используемого физического принципа бывают оптиче-
ские, магнитные и электрические кодовые маски.
Кодовая маска угловых перемещений представляет собой диск,
поверхность которого разбивается на ряд концентрических окруж-
ностей (число образовавшихся колец равно числу разрядов кода) и
на сектора (число секторов в пределах кольца соответствует количе-
ству возможных кодовых комбинаций и определяет точность измере-
ния углового перемещения). Этот диск соединяется с каким-либо
чувствительным элементом, например трубкой Бурдона, и при из-
менении контролируемого параметра поворачивается на определен-
ный угол. В электрических масках сектора делаются по определенно-
му правилу проводящими и непроводящими, а диск вращается от-
носительно неподвижных щеток. В оптических масках сектора
кодовой маски делаются оптически прозрачными или непрозрачны-
ми, а сам диск вращается между несколькими источниками оптиче-
ского излучения и расположенными напротив них фотоэлементами.
В магнитных кодовых масках секторами диска экранируется магнит-
ное поле. Источником магнитного поля могут быть или постоянные
магниты, или электромагниты. В качестве чувствительных элементов
могут использоваться магнитоуправляемые контакты (герконы) или
преобразователи Холла.
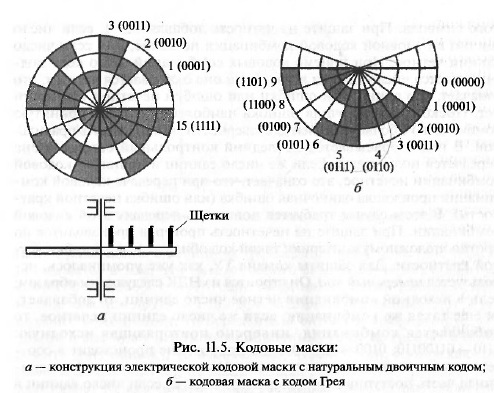
Электрическая кодовая маска углового перемещения приведена
на рис. 11.5, а. Чередование проводящих и непроводящих участков
подчиняется закону натурального двоичного кода. Считывание кода
производится с помощью неподвижных щеток, расположенных по
радиусу диска. Младший разряд располагается у края диска. Изме-
нение углового положения диска вызывает изменение считываемого
кода. В результате считанный двоичный код является функцией угло-
вого положения диска. Недостатком кодовой маски НДК является
возможность возникновения больших погрешностей во время пере-
хода из одного положения в другое. Эта погрешность, называемая
погрешностью от неопределенности считывания, обусловлена не-
одновременным изменением цифр в разных разрядах вследствие
несовершенства аппаратуры. Так, при переходе щеток из положения
5 (0101) в положение 6 (0110) ошибка считывания может возникнуть
в двух младших разрядах. Фактически могут быть прочитаны кодовые
комбинации 0100, 0101, 0110 и 0111, что соответствует положениям
диска 4, 5, 6 и 7 соответственно. Из них комбинации 0100 и 0111 яв-
ляются ложными, т. е. их появление на выходе считывающего устрой-
ства приведет к возникновению погрешности. Этого недостатка
лишена кодовая маска, в которой чередование проводящих и непро-
водящих участков подчинено закону кода Грея (рис. 11.5, б). Код Грея
образуется из комбинации НДК путем суммирования по модулю два
с точно такой же комбинацией, смещенной на один разряд влево или
вправо. Сложение (суммирование) по модулю 2 — это так называемое
логическое сложение. Знак этой операции обозначается символом ©.
При логическом сложении сумма двух разных символов равна 1, а
двух одинаковых — 0. Младший разряд полученной комбинации от-
брасывается. Например, результат перевода из НДК в код Грея ком-
бинации 1011: 1011 (НДК) = >1110 (код Грея):
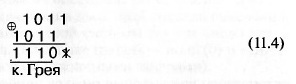
При обратном преобразовании кода Грея в НДК старший разряд
кодовой комбинации остается тот же, а каждый последующий разряд
получается как результат логического сложения всех разрядов кода
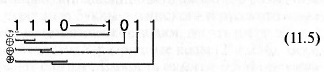
Грея, начиная со старшего и заканчивая преобразуемым разрядом.
Результат перевода: 1110 (код Грея) =>1011 (НДК):
В коде Грея соседние кодовые комбинации различаются только в
одном разряде. В результате максимальная абсолютная погрешность
считывания не превышает одной единицы. Благодаря этому качеству
код Грея нашел широкое применение в преобразователях угловых и
линейных перемещений.
Однако при использовании этого кода необходимо помнить, что
код Грея'неарифметический, т.е. в нем отсутствует постоянный вес
разряда, поэтому над ним нельзя производить арифметические опе-
рации. Кроме того, имеются определенные трудности перевода кода
Грея в десятичный код и обратно.
Контрольные вопросы
1. Перечислите базовые функции системы телемеханики.
2. В чем заключается разница между телеуправлением и телерегулированием?
3. Охарактеризуйте понятия «линия связи» и «канал связи».
4. Какие виды сигнала вы знаете?
5. Одинаковы ли по смыслу понятия «сообщение» и «информация»?
6. На какие группы делятся сообщения в зависимости от характера изме-
нения во времени?
7. Из каких соображений определяется число уровней квантования?
8. Какие импульсные признаки сигнала существуют?
9. Что такое кодирование?
10. Почему при передаче сообщений в системах телемеханики наибольшее
распространение получили двоичные коды?
11. Почему в кодовых масках используется код Грея?
Гл а в а 12
Дата: 2018-12-28, просмотров: 642.