Силы, приложенные к твердому телу в точке, называются сосредоточенными. Однако, реально существуют лишь системы распределенных сил, приложенных к телу по объему,по поверхности, или по линии. Распределенные силы характеризуются величиной силы приходящейся на единицу объема, площади или длины тела.
В основном действуют параллельные системы распределенных сил. Например: силы тяжести, силы давления ветра на стену здания, воды на плотину, сыпучего груза на площадку и т.д.
Для сил, распределенных по отрезку прямой (рис. 1.9), интенсивность q – частное от деления равнодействующей dQ системы сил, приложенных к бесконечно малому участку линии, на длину dx этого участка.
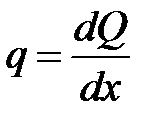, Н/м.
Рис. 1.9
При известном законе изменения q=f(x) (рис. 1.9) равнодействующая распределенной нагрузки определиться по формуле
.
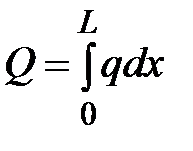В соответствии с теоремой о моменте равнодействующей, выражение для определения точки приложения силы Q имеет вид:
; 
.
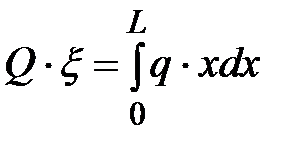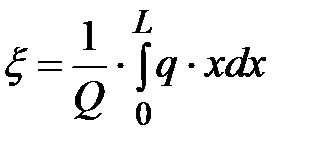Для нагрузки, изменяющейся по линейному закону (рис.1.10) и (рис.1.11), формулы для определения Q и ξ имеют вид:
| 
|
| Рис. 1.10. | Рис. 1.11 |
| 
|
Задача
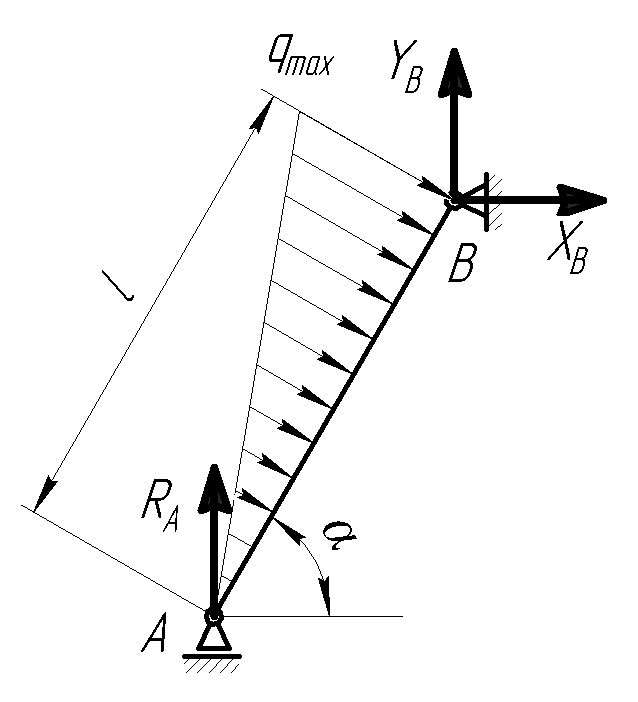
Определить реакцию опоры А, если длина балки l = 0,3 м, интенсивность распределенной нагрузки qmax = 20 Н/м, угол α = 60º.
___________________________________
Решение:
Применим принцип освобождаемости от связей, заменив связи их реакциями.
Составим уравнение равновесия: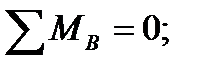 
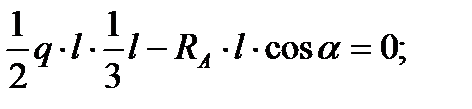
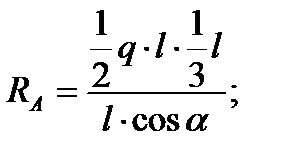
Подставляя численные значения получим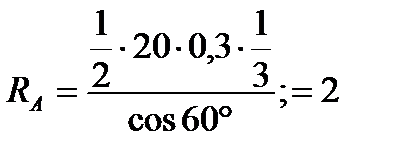 
Н.
Ответ: R А = 2 Н.
Момент силы относительно оси
Момент MZ силы относительно оси Oz (рис.1.12) равен произведению модуля проекции силы на плоскость Q, перпендикулярную оси, на плечо h этой проекции относительно точки O пересечения оси с плоскостью Q.
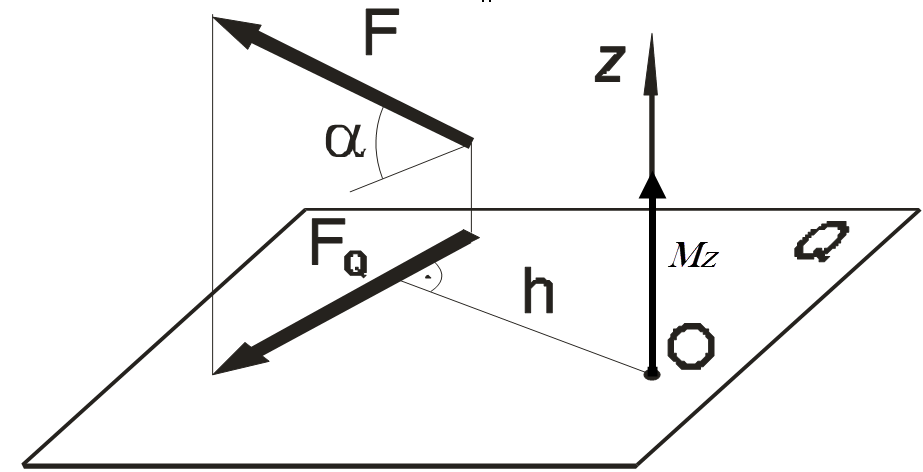
Рис.1.12
.
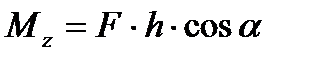Момент считается положительным, если, (см. рис.1.12) смотреть навстречу оси, «вращение» плоскости Q под действием спроецированной на неё силы наблюдается происходящим против хода часовой стрелки, и отрицательным – при вращении в обратном направлении.
Момент силы относительно оси равен нулю, если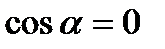 
(линия действия силы параллельна оси); или h=0 (линия действия силы проходит через ось).
Момент силы относительно осей и начала отсчета прямоугольной системы координат (рис. 1.13) можно определить через координаты точки приложения силы (x, y, z) и проекции силы на оси (X, Y, Z).
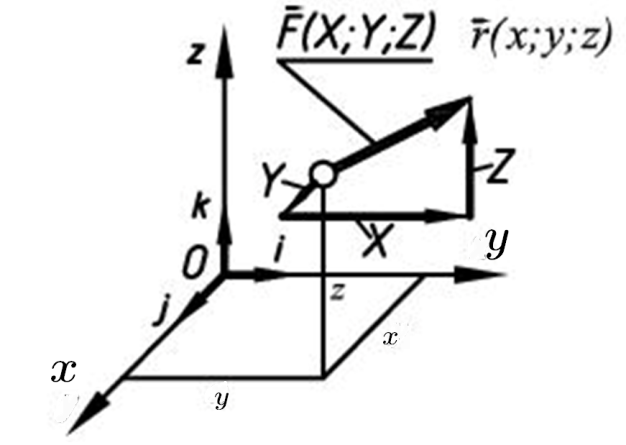
Рис. 1.13
;
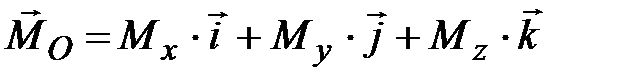Mx=yZ-zY; My=zX-xZ; Mz=xY-yX;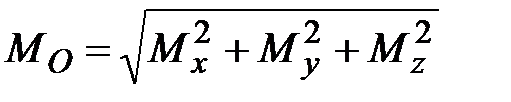 
,
где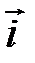 
, 
и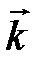 
– еденичные орты осей координатx, y, z соответственно.
Задача
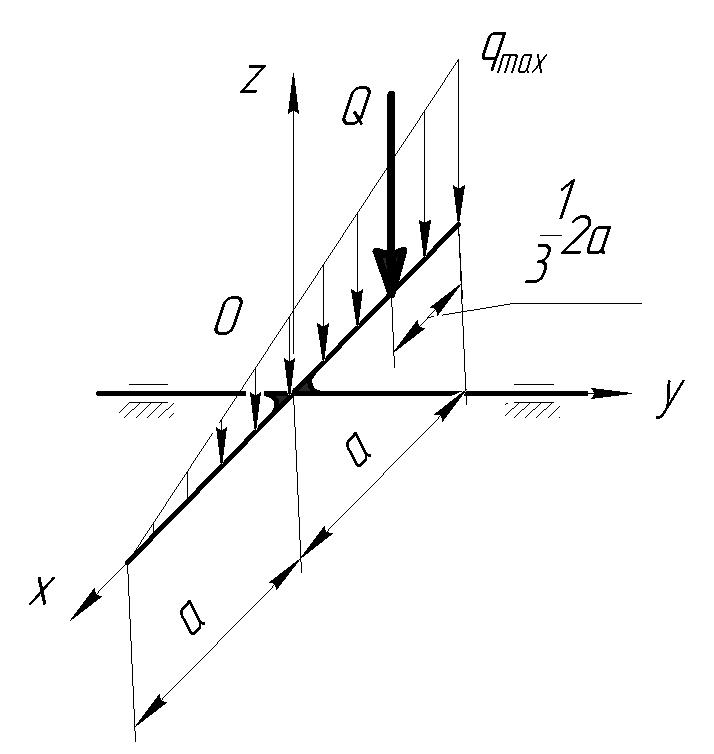
Определить момент распределенной нагрузки относительно оси O y, если
qmax = 10 Н/м, а = 3 м.
________________________________
Решение:
Момент распределенной нагрузки относительно оси Oy равен:
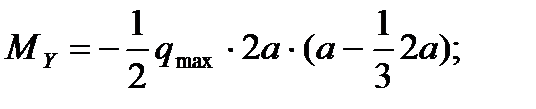
Подставляя численные значения получим
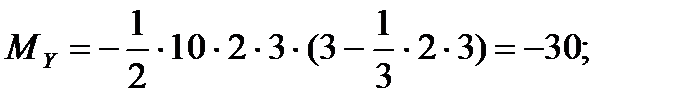Н∙м.
Ответ: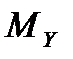 
= –30 Н∙м.
Дата: 2018-12-28, просмотров: 777.
