3.1. Пределы, непрерывность и разрывы функций.
3.1.1.Найти пределы функций:
а) 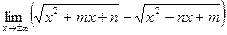 ;
;
б) 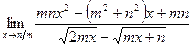 ;
;
в) 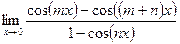 ;
;
г) 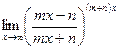 .
.
3.1.2.В точках 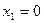 и
и 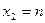 для функции
для функции 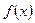 установить непрерывность или определить характер точек разрыва. Нарисовать график функции
установить непрерывность или определить характер точек разрыва. Нарисовать график функции 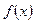 в окрестностях этих точек:
в окрестностях этих точек:
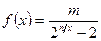 ;
;
Производные функций.
3.1.3.Найти производные 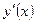 функций:
функций:
а) 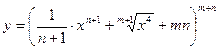 ; б)
; б) 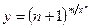 ;
;
в) 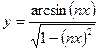 ; д)
; д) 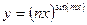 ; е)
; е) 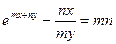 ;
;
ж) 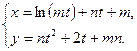
3.2. Приложения производной.
3.2.1.С помощью методов дифференциального исчисления построить график функции 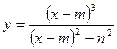 .
.
3.3. Приближенное решение алгебраических уравнений.
3.3.1.Для уравнения 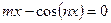 отделить положительный корень и найти его приближенно с точностью
отделить положительный корень и найти его приближенно с точностью 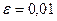 :
:
а) методом деления отрезка пополам;
б) методом касательных.
Примечание. Можно считать, что точность 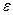 достигнута, если разность между соседними приближениями
достигнута, если разность между соседними приближениями 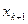 и
и 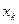 удовлетворяет неравенству
удовлетворяет неравенству 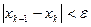 .
.
4. Интегральное исчисление.
4.1. Неопределенный интеграл.
4.1.1.Найти интегралы:
а) 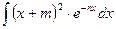 ; б)
; б) 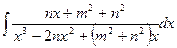 ; д)
; д) 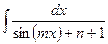 .
.
4.2. Несобственные интегралы.
4.2.1.Вычислить интеграл или установить его расходимость:
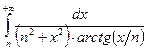
4.3. Применения определенных интегралов.
4.3.1.Построить схематический чертеж и найти площадь фигуры, ограниченной линиями:
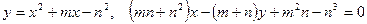 ;
;
4.3.2.Найти объем тела, полученного при вращении вокруг оси ОХ фигуры, ограниченной линиями:
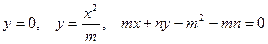 .
.
4.4. Приближенное вычисление определенных интегралов.
4.4.1.Для вычисления определенного интеграла 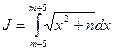 , разбивая отрезок интегрирования сначала на 10 равных частей, а затем на 20 равных частей, найти приближенное значение
, разбивая отрезок интегрирования сначала на 10 равных частей, а затем на 20 равных частей, найти приближенное значение 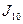 и
и 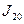 : а) по формуле трапеций; б) по формуле Симпсона. Оценить точность приближения с помощью разности
: а) по формуле трапеций; б) по формуле Симпсона. Оценить точность приближения с помощью разности 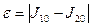 .
.
5. Функции нескольких переменных.
5.1. Частные производные и дифференциал функции.
5.1.1.Найти дифференциал 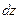 функции
функции 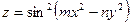 .
.
5.1.2.Показать, что функция 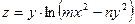 удовлетворяет уравнению
удовлетворяет уравнению 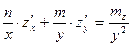 .
.
5.2. Приложения частных производных.
5.2.1.Составить уравнения касательной плоскости и нормали к поверхности 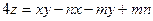 в точке
в точке 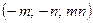 .
.
5.2.2.Для функции 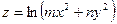 в точке
в точке 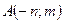 найти градиент и производную по направлению
найти градиент и производную по направлению 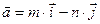 .
.
6. Двойные, тройные и криволинейные интегралы.
6.1. Двойные интегралы.
6.1.1.Изменить порядок интегрирования:
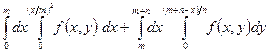 .
.
6.1.2.Сделать чертеж и найти объем тела, ограниченного поверхностями 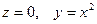 и плоскостью, проходящей через точки
и плоскостью, проходящей через точки 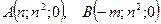 и
и 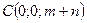 .
.
6.1.3.Сделать чертеж и найти площадь фигуры, ограниченной линиями:
а) 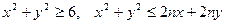 .
.
6.2. Тройные интегралы.
6.2.1.Найти 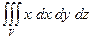 , если тело V ограниченно плоскостями
, если тело V ограниченно плоскостями 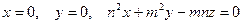 и
и 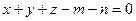 .
.
6.2.2.Найти объем тела, ограниченного поверхностями 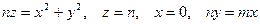 .
.
6.3. Криволинейные интегралы.
6.3.1.Вычислить 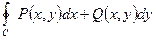 , где
, где 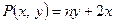 ,
, 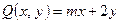 , а контур С образован линиями
, а контур С образован линиями 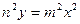 ,
, 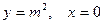 : а) непосредственно; б) по формуле Грина.
: а) непосредственно; б) по формуле Грина.
6.3.2.Вычислить 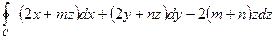 , где контур С является одним витком винтовой линии:
, где контур С является одним витком винтовой линии:
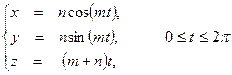 .
.
7. Элементы теории поля.
7.1. Дифференциальные операции.
7.1.1.В точке 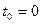 составить уравнение касательной прямой и нормальной плоскости к кривой
составить уравнение касательной прямой и нормальной плоскости к кривой
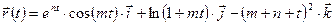 .
.
7.1.2.Найти в точке 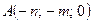 градиент скалярного поля
градиент скалярного поля
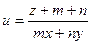 .
.
7.1.3.Найти в точке 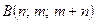 дивергенцию векторного поля
дивергенцию векторного поля
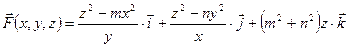 .
.
7.1.4.Найти в точке 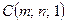 ротор векторного поля
ротор векторного поля
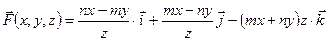 .
.
7.2. Интегралы и интегральные теоремы.
7.2.1.Убедиться, что поле 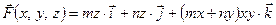 потенциально, и найти его потенциал.
потенциально, и найти его потенциал.
7.2.2.Даны поле 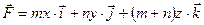 и цилиндр D, ограниченный поверхностями z =0, z = m , x 2 + y 2 =( n +1)2. Найти:
и цилиндр D, ограниченный поверхностями z =0, z = m , x 2 + y 2 =( n +1)2. Найти:
а) поток поля 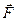 через боковую поверхность цилиндра в направлении внешней нормали;
через боковую поверхность цилиндра в направлении внешней нормали;
б) поток поля 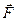 через всю поверхность цилиндра в направлении внешней нормали непосредственно и с помощью теоремы Остроградского – Гаусса.
через всю поверхность цилиндра в направлении внешней нормали непосредственно и с помощью теоремы Остроградского – Гаусса.
7.2.3. Даны поле 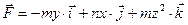 и замкнутый виток
и замкнутый виток 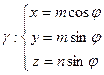 ,
, 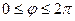 ( обход контура происходит в направлении, соответствующем возрастанию параметра φ). Найти циркуляцию поля
( обход контура происходит в направлении, соответствующем возрастанию параметра φ). Найти циркуляцию поля 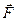 вдоль контура γ непосредственно и с помощью теоремы Стокса.
вдоль контура γ непосредственно и с помощью теоремы Стокса.
8. Дифференциальные уравнения.
8.1. Уравнения первого порядка.
8.1.1.Найти общее решение уравнения:
а) 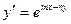 ; б)
; б) 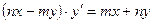 ; в)
; в) 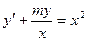 .
.
8.1.2.Скорость роста банковского вклада пропорциональна с коэффициентом равным 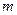 величине вклада. Найти закон изменения величины вклада со временем, если первоначальная сумма вклада составляла
величине вклада. Найти закон изменения величины вклада со временем, если первоначальная сумма вклада составляла 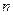 миллионов рублей.
миллионов рублей.
8.2. Линейные уравнения высших порядков.
8.2.1.Решить задачу Коши:
а) 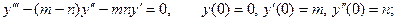
б) 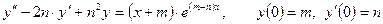 .
.
8.3. Системы линейных уравнений.
8.3.1.Решить систему линейных уравнений
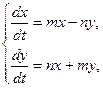 с начальными условиями
с начальными условиями 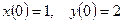 .
.
9. Ряды.
9.1. Числовые ряды.
9.1.1.Исследовать на сходимость ряды с положительными членами:
а) 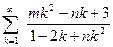 ; б)
; б) 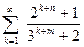 ;
;
в) 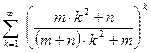 ; г)
; г) 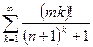 .
.
9.1.2.Исследовать на условную сходимость и абсолютную сходимость знакочередующиеся ряды:
а) 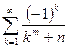 ; б)
; б) 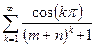 .
.
9.2. Степенные ряды.
9.2.1.Найти область сходимости степенного ряда:
а) 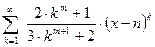 ; б)
; б) 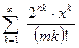 .
.
9.2.2.Разложить функцию 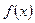 в ряд Тейлора в окрестности точки х0:
в ряд Тейлора в окрестности точки х0:
а) 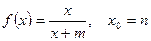 ; б)
; б) 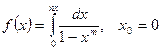 .
.
9.2.3.С помощью разложения в ряд вычислить приближенно с точностью 0,001 значения:
а) 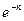 ; б)
; б) 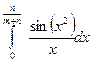 .
.
9.3. Ряды Фурье.
9.3.1.Разложить функцию 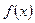 в ряд Фурье в указанном интервале:
в ряд Фурье в указанном интервале:
а) 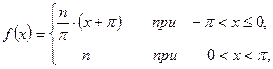
в интервале 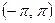 ;
;
б) 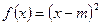 в интервале
в интервале 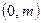 .
.
в) 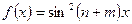 в интервале
в интервале 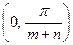 .
.
10. Функции комплексного переменного.
10.1. Действия с комплексными числами.
10.1.1. Выполнить действия:
а) 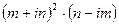 ; б)
; б) 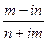 .
.
10.1.2. Решить уравнения:
а) 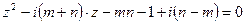 ; б)
; б) 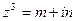 .
.
10.2. Аналитические функции.
10.2.1. Показать, что функция 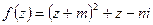 аналитична.
аналитична.
10.2.2. Известна вещественная часть u ( x , y )= m ( x 2 - y 2 )+ mx - ny аналитической функции f ( z ), (z = x + iy). Найти функцию f(z) .
10.3. Интегрирование функций комплексного переменного.
10.3.1. Вычислить 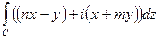 , где контур С – незамкнутая ломанная, соединяющая точки
, где контур С – незамкнутая ломанная, соединяющая точки 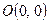 ,
, 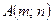 и
и 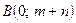 .
.
10.3.2. Вычислить с помощью интегральной формулы Коши
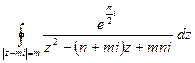 .
.
10.4. Ряды Тейлора и Лорана.
10.4.1. Разложить функцию 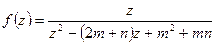 в окрестности точки
в окрестности точки 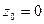 в ряд Тейлора и найти радиус сходимости ряда.
в ряд Тейлора и найти радиус сходимости ряда.
10.4.2. Разложить функцию 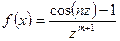 в окрестности точки
в окрестности точки 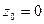 в ряд Лорана.
в ряд Лорана.
10.4.3. Разложить функцию 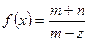 в ряд Лорана по степеням
в ряд Лорана по степеням 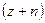 и найти область сходимости ряда.
и найти область сходимости ряда.
10.5. Вычеты и их приложения.
10.5.1. Определить тип особых точек функции 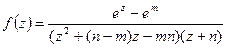 и найти вычеты в конечных особых точках.
и найти вычеты в конечных особых точках.
10.5.2. Вычислить с помощью вычетов 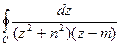 , где контур C , заданный уравнением
, где контур C , заданный уравнением 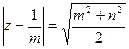 , обходится против часовой стрелки.
, обходится против часовой стрелки.
11. Операционное исчисление.
11.1. Нахождение изображений и восстановление оригиналов.
11.1.1. Найти изображения функций:
а) 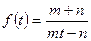 ; б)
; б) 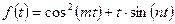 .
.
11.1.2. Восстановить оригиналы по изображениям:
а) 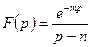 ; б)
; б) 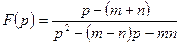 .
.
11.2. Приложения операционного исчисления.
11.2.1. Решить операционным методом дифференциальное уравнение:
а) 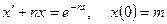 ;
;
б) 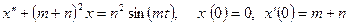 .
.
12. Теория вероятностей.
12.1. Случайные события.
12.1.1. В коробке находятся m +2 синих, n +3 красных и 2 n +1 зеленых карандашей. Одновременно вынимают m +3 n +2 карандашей. Найти вероятность того, что среди них будет m +1 синих и n +1 красных.
12.1.2. В первой урне находятся m +2 шаров белого и n шаров черного цвета, во второй — m + n белого и m синего, в третьей — n +3 белого и m +1 красного цвета. Из первой и второй урны наудачу извлекают по одному шару и кладут в третью. После этого из третьей вынимают один шар. Найти вероятность того, что он окажется белым.
12.1.3. Вероятность попадания стрелка в мишень при одном выстреле равна 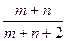 . Производится n+4 выстрела. Найти вероятность того, что он промахнется не более двух раз.
. Производится n+4 выстрела. Найти вероятность того, что он промахнется не более двух раз.
12.2. Случайные величины.
12.2.1. Случайная величина Х равна числу появлений «герба» в серии из n +3 бросаний монеты. Найти закон распределения и функцию распределения F ( x ) этой случайной величины; вычислить ее математическое ожидание MX и дисперсию DX; построить график F(x).
12.2.2. Закон распределения дискретной случайной величины X имеет вид:
| xi | -2 | -1 | 0 | m | m+n |
| pi | 0,2 | 0,1 | 0,2 | p4 | p5 |
Найти вероятности p 4 , p 5 , и дисперсию DX, если математическое ожидание MX=-0,5+0,5m+0,1n.
12.2.3. Плотность распределения непрерывной случайной величины X имеет вид:
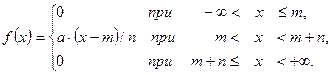
Найти:
а) параметр а; б) функцию распределения 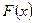 ;
;
в) вероятность попадания случайной величины X в интервал
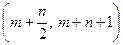 ;
;
г) математическое ожидание MX и дисперсию DX.
Построить график функций 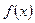 и
и 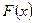 .
.
12.2.4. Случайные величины 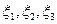 имеют равномерное, пуассоновское и показательное распределения соответственно. Известно, что математические ожидания Mξi = m + n , а дисперсия Dξ 1 = n 2 /3. Найти вероятности: а)
имеют равномерное, пуассоновское и показательное распределения соответственно. Известно, что математические ожидания Mξi = m + n , а дисперсия Dξ 1 = n 2 /3. Найти вероятности: а) 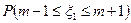 ; б)
; б) 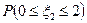 ; в)
; в) 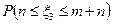 .
.
13. Элементы математической статистики
Имеются следующие выборочные данные (выборка 10%-ная, механическая) о выпуске продукции и сумме прибыли, млн. руб.:
| № предприятия | Выпуск продукции | Прибыль | № предприятия | Выпуск продукции | Прибыль |
| 1 | 60+n | 15,7 | 16 | 52,0 | 14,6 |
| 2 | 78,0 | 18,0 | 17 | 62,0 | 14,8 |
| 3 | 41,0 | 12,1 | 18 | 69,0 | 16,1 |
| 4 | 54,0 | 13,8 | 19 | 85,0 | 16,7 |
| 5 | 60+n | 15,5 | 20 | 70+n | 15,8 |
| 6 | n•m+20 | n+m+10 | 21 | 71,0 | 16,4 |
| 7 | 45,0 | 12,8 | 22 | n•m+30 | n+m+20 |
| 8 | 57,0 | 14,2 | 23 | 72,0 | 16,5 |
| 9 | 67,0 | 15,9 | 24 | 88,0 | 18,5 |
| 10 | 80+n | 17,6 | 25 | 70+n | 16,4 |
| 11 | 92,0 | 18,2 | 26 | 74,0 | 16,0 |
| 12 | 48,0 | n+m+5 | 27 | 96,0 | 19,1 |
| 13 | 59,0 | 16,5 | 28 | 75,0 | 16,3 |
| 14 | 68,0 | 16,2 | 29 | 101,0 | 19,6 |
| 15 | 80+n | 16,7 | 30 | 70+n | 17,2 |
По исходным данным:
Задание 13. 1.
13.1.1. Постройте статистический ряд распределения предприятий по сумме прибыли, образовав пять групп с равными интервалами. Постройте графики ряда распределения.
13.1.2. Рассчитайте числовые характеристики ряда распределения предприятий по сумме прибыли: среднюю арифметическую 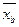 , среднее квадратическое отклонение
, среднее квадратическое отклонение 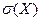 , дисперсию, коэффициент вариации V. Сделайте выводы.
, дисперсию, коэффициент вариации V. Сделайте выводы.
Задание 13.2.
13.2.1. Определите границы, в которых с вероятностью 0,997 заключена сумма прибыли одного предприятия в генеральной совокупности.
13.2.2. Используя c2-критерий Пирсона, при уровне значимости 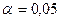 проверить гипотезу о том, что случайная величина X – сумма прибыли – распределена по нормальному закону.
проверить гипотезу о том, что случайная величина X – сумма прибыли – распределена по нормальному закону.
Задание 13.3.
13.3.1. Установите наличие и характер корреляционной связи между стоимостью произведённой продукции (X) и суммой прибыли на одно предприятие (Y). Постройте диаграмму рассеяния и линию регрессии.
13.3.2. Определите коэффициенты выборочного уравнения регрессии 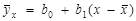 .
.
13.3.3. Рассчитайте линейный коэффициент корреляции. Используя t-критерий Стьюдента, проверьте значимость коэффициента корреляции. Сделайте вывод о тесноте связи между факторами X и Y, используя шкалу Чеддока.
При расчетах целесообразно использовать стандартные математические пакеты для персональных компьютеров.
14. Линейное программирование.
14.1. Задача оптимального производства продукции.
Предприятие планирует выпуск двух видов продукции I и II, на производство которых расходуется три вида сырья А, В, и С. Потребность 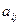 на каждую единицу
на каждую единицу 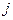 -го вида продукции
-го вида продукции 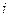 -го вида сырья, запас
-го вида сырья, запас 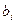 соответствующего вида сырья и прибыль
соответствующего вида сырья и прибыль 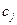 от реализации единицы
от реализации единицы 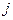 -го вида продукции заданы таблицей:
-го вида продукции заданы таблицей:
| Виды сырья | Виды продукции | Запасы сырья | |
| I | II | ||
| А | 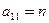
| 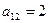
| 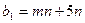
|
| В | 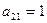
| 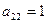
| 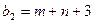
|
| С | 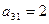
| 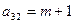
| 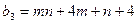
|
| прибыль | 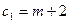
| 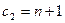
| |
| план (ед.) | 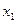
| 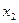
| |
14.1.1. Для производства двух видов продукции I и II с планом 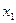 и
и 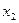 единиц составить целевую функцию прибыли Z и соответствующую систему ограничений по запасам сырья, предполагая, что требуется изготовить в сумме не менее
единиц составить целевую функцию прибыли Z и соответствующую систему ограничений по запасам сырья, предполагая, что требуется изготовить в сумме не менее 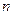 единиц обоих видов продукции.
единиц обоих видов продукции.
14.1.2. В условиях задачи 14.1.1. составить оптимальный план 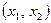 производства продукции, обеспечивающий максимальную прибыль
производства продукции, обеспечивающий максимальную прибыль 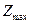 . Определить остатки каждого вида сырья. (Задачу решить симплекс – методом)
. Определить остатки каждого вида сырья. (Задачу решить симплекс – методом)
14.1.3. Построить по полученной системе ограничений многоугольник допустимых решений и найти оптимальный план производства геометрическим путем. Определить соответствующую прибыль 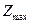 .
.
14.2. Транспортная задача.
На трех складах 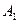 ,
, 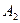 и
и 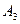 хранится
хранится 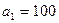 ,
, 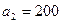 и
и 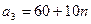 единиц одного и того же груза. Этот груз требуется доставить трем потребителям
единиц одного и того же груза. Этот груз требуется доставить трем потребителям 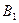 ,
, 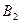 и
и 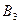 , заказы которых составляют
, заказы которых составляют 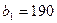 ,
, 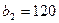 и
и 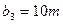 единиц груза соответственно. Стоимость перевозок
единиц груза соответственно. Стоимость перевозок 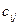 единицы груза с
единицы груза с 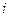 -го склада
-го склада 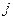 -му потребителю указаны в правых верхних углах соответствующих клеток транспортной таблицы:
-му потребителю указаны в правых верхних углах соответствующих клеток транспортной таблицы:
|
запасы | 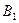
| 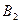
| 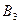
| |
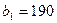
| 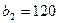
| 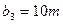
| ||
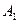
| 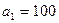
|  4 4
|  2 2
|  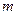
|
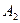
| 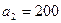
|  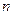
|  5 5
|  3 3
|
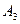
| 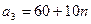
|  1 1
|  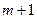
|  6 6
|
14.2.1. Сравнивая суммарный запас 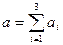 и суммарную потребность
и суммарную потребность 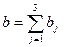 в грузе, установить, является ли модель транспортной задачи, заданная этой таблицей, открытой или закрытой. Если модель является открытой, то ее необходимо закрыть, добавив фиктивный склад
в грузе, установить, является ли модель транспортной задачи, заданная этой таблицей, открытой или закрытой. Если модель является открытой, то ее необходимо закрыть, добавив фиктивный склад 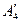 с запасом
с запасом 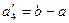 в случае
в случае 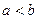 или фиктивного потребителя
или фиктивного потребителя 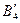 с потребностью
с потребностью 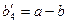 в случае
в случае 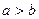 и положив соответствующие им тарифы перевозок нулевыми.
и положив соответствующие им тарифы перевозок нулевыми.
14.2.2. Составить первоначальный план перевозок. (Рекомендуется воспользоваться методом наименьшей стоимости.)
14.2.3. Проверить, является ли первоначальный план оптимальным в смысле суммарной стоимости перевозок, и если это так, то составить оптимальный план
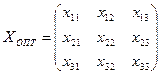 ,
,
обеспечивающий минимальную стоимость перевозок 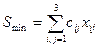 . Найти эту стоимость. (Рекомендуется воспользоваться методом потенциалов.)
. Найти эту стоимость. (Рекомендуется воспользоваться методом потенциалов.)
14.3. Матричные игры.
14.3.1. Игра 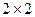 задана матрицей
задана матрицей
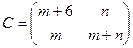
Найти вероятности применения стратегий 1-м и 2-м игроком для получения цены игры. (Задачу решить аналитическим методом.)
14.3.2. Игра задана матрицами
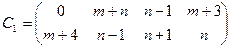 для
для 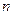 - четного
- четного
и
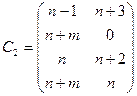 для
для 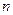 - нечетного.
- нечетного.
Применяя графический метод, найти смешанные оптимальные стратегии обоих игроков и определить цену игры.
15. Математические методы в экономике .
15.1. Сетевое планирование.
Прогресс производства сложной продукции разбивается на отдельные этапы, зашифрованные номерами 1, 2,..., 10. 1 – начальный этап производства продукции, 10 – завершающий. Переход от 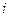 -го этапа к
-го этапа к 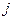 -му этапу назовем операцией. Возможны выполнения операций
-му этапу назовем операцией. Возможны выполнения операций 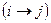 и их продолжительности
и их продолжительности 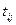 задаются таблицей.
задаются таблицей.
| N п/п | шифр операции | продолжительность операции | 15.1.1. Составьте и упорядочите по слоям сетевой график производства работ. Номера этапов необходимо обвести кружками, а операции |
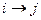
| 
| ||
| 1 | 1→2 | 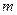
| |
| 2 | 1→3 | 4 | |
| 3 | 1→4 | 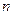
| |
| 4 | 2→3 | 3 | |
| 5 | 2→6 | 5 | |
| 6 | 4→3 | 2 | |
| 7 | 4→6 | 6 | |
| 8 | 3→5 | 3 | 15.1.2. Считая, что начало работы происходит во время |
| 9 | 3→7 | 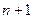
| |
| 10 | 5→9 | 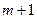
| |
| 11 | 6→7 | 4 | |
| 12 | 6→8 | 3 | |
| 13 | 7→8 | 7 | |
| 14 | 7→9 | 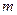
| |
| 15 | 7→10 | 5 | |
| 16 | 8→10 | 4 | |
| 17 | 9→10 | 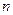
|
15.1.3. Найдите критическое время завершения процесса работ Ткр и выделите стрелки, лежащие на критическом пути.
15.1.4. Для каждой некритической операции 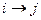 определите резервы свободного времени
определите резервы свободного времени 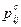 и проставьте их над стрелками рядом с
и проставьте их над стрелками рядом с 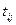 в скобках.
в скобках.
15.1.5. Решите задачу табличным методом. Номера этапов, лежащие на критическом пути подчеркните. (В табличном методе кроме резервов свободного времени 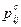 необходимо также найти полные резервы времени
необходимо также найти полные резервы времени 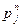 для каждого этапа.)
для каждого этапа.)
Дата: 2018-12-28, просмотров: 324.
 потребности
потребности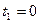 , определите время
, определите время 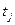 окончания каждого
окончания каждого