СБОРНИК ЗАДАНИЙ
ПО МАТЕМАТИКЕ
Контрольные задания и программа по курсам математики и математических методов в экономике
для студентов заочного отделения
Санкт-Петербург
2005
Утверждены Методическим Советом СПбГАСЭ
Сборник заданий по математике. Контрольные задания и программа по курсам математики и математических методов в экономике для студентов заочного отделения. - СПб.: Изд-во СПбГАСЭ, 2005. – 32 с.
Сборник содержит задачи для контрольных работ по всем курсам математических дисциплин, предусмотренным учебными планами специальностей, и краткий перечень вопросов для подготовки к экзаменам.
Каждая контрольная работа состоит из задач одного или нескольких разделов данного сборника, выбранных в соответствии с рабочей программой.
Перечень разделов сборника, необходимых для выполнения контрольных работ по каждой специальности, сообщается студентам этой специальности в начале семестра.
Составители: канд. физ.-мат. наук, проф. С.И.Никитин;
канд. физ.-мат. наук, доц. А.Л.Пирозерский;
канд. физ.-мат. наук, доц. Н.Ю.Кропачева;
старший преподаватель М.Ю.Никанорова.
© Санкт-Петербургская государственная академия сервиса и экономики
2005 г.
Содержание
Требования к оформлению контрольных работ ...................................... 4
Формирование исходных данных к задачам ............................................ 4
Раздел 1. Линейная алгебра .................….............................................. 5
Раздел 2. Аналитическая геометрия ...................................................... 6
Раздел 3. Дифференциальное исчисление............................................. 7
Раздел 4. Интегральное исчисление ...................................................... 8
Раздел 5. Функции нескольких переменных ........................................ 9
Раздел 6. Двойные, тройные и криволинейные интегралы ................. 9
Раздел 7. Элементы теории поля ........................................................... 10
Раздел 8. Дифференциальные уравнения .............................................. 11
Раздел 9. Ряды .......................................................................................... 12
Раздел 10. Функции комплексного переменного ................................... 13
Раздел 11. Операционное исчисление ..................................................... 14
Раздел 12. Теория вероятностей .............................................................. 15
Раздел 13. Математическая статистика .................................................. 16
Раздел 14. Линейное программирование ................................................ 18
Раздел 15. Математические методы в экономике .................................. 21
Раздел 16. Дискретная математика .......................................................... 23
Краткое содержание (программа) курса.................................................... 25
Список учебной литературы ...................................................................... 31
Требования к оформлению контрольных работ
1. Контрольные работы следует выполнять в ученических тетрадях в клетку. На обложке необходимо указать: название института Академии; название кафедры (математики и математических методов в экономике); название и номер контрольной работы; название (номер) специальности; фамилию, имя, отчество и личный шифр студента.
2. На каждой странице надо оставить поля размером 4 см для оценки решения задач и методических указаний проверяющего работу.
3. Условия задач переписывать полностью необязательно, достаточно указать номер задачи по данному сборнику. В условия задач надо сначала подставить конкретные числовые значения параметров т и п, и только после этого приступать к их решению.
4. Задачи в контрольной работе нужно располагать в порядке возрастания номеров.
Формирование исходных данных к задачам
Каждая контрольная работа состоит из задач одного или нескольких разделов сборника.
Условия задач, входящих в контрольную работу, одинаковы для всех студентов, однако числовые данные задач зависят от личного шифра студента, выполняющего работу.
Числовых данных параметров т и п определяются по двум последним цифрам своего шифра (А — предпоследняя цифра, В — последняя цифра). Значение параметра т выбирается из таблицы 1, а значение параметра п - из таблицы 2. Эти два числа т и п и нужно подставить в условия задач контрольной работы.
Таблица 1 (выбор параметра т)
| А | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| т | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Таблица 2 (выбор параметра п )
| В | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| п | 5 | 3 | 2 | 4 | 1 | 4 | 5 | 2 | 3 | 1 |
Например, если шифр студента 1604 — 037, то А = 3, В = 7, и из таблиц находим, что т = 4, п = 2. Полученные т = 4 и п = 2 подставляются в условия всех задач контрольной работы этого студента.
Линейная алгебра
Действия с матрицами.
Выполнить действия:
а) 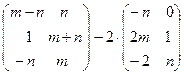 ; б)
; б) 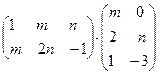 .
.
Вычисление определителей.
Вычислить определитель 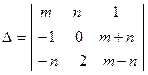 двумя способами:
двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
Обратная матрица.
Найти обратную матрицу к матрице 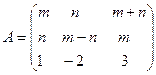 и проверить выполнение равенства
и проверить выполнение равенства 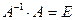 .
.
Системы линейных уравнений.
Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) с помощью вычисления обратной матрицы, записав систему в матричном виде 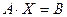 :
:
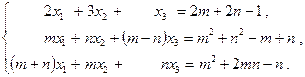
Аналитическая геометрия
Прямая на плоскости.
Построить треугольник, вершины которого находятся в точках 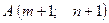 ,
, 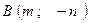 ,
, 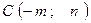 и найти:
и найти:
1) координаты точки пересечения медиан;
2) длину и уравнение высоты, опущенной из вершины А;
3) площадь треугольника;
4) систему неравенств, задающих внутренность треугольника АВС.
Задание 13. 1.
13.1.1. Постройте статистический ряд распределения предприятий по сумме прибыли, образовав пять групп с равными интервалами. Постройте графики ряда распределения.
13.1.2. Рассчитайте числовые характеристики ряда распределения предприятий по сумме прибыли: среднюю арифметическую 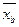 , среднее квадратическое отклонение
, среднее квадратическое отклонение 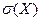 , дисперсию, коэффициент вариации V. Сделайте выводы.
, дисперсию, коэффициент вариации V. Сделайте выводы.
Задание 13.2.
13.2.1. Определите границы, в которых с вероятностью 0,997 заключена сумма прибыли одного предприятия в генеральной совокупности.
13.2.2. Используя c2-критерий Пирсона, при уровне значимости 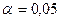 проверить гипотезу о том, что случайная величина X – сумма прибыли – распределена по нормальному закону.
проверить гипотезу о том, что случайная величина X – сумма прибыли – распределена по нормальному закону.
Задание 13.3.
13.3.1. Установите наличие и характер корреляционной связи между стоимостью произведённой продукции (X) и суммой прибыли на одно предприятие (Y). Постройте диаграмму рассеяния и линию регрессии.
13.3.2. Определите коэффициенты выборочного уравнения регрессии 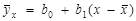 .
.
13.3.3. Рассчитайте линейный коэффициент корреляции. Используя t-критерий Стьюдента, проверьте значимость коэффициента корреляции. Сделайте вывод о тесноте связи между факторами X и Y, используя шкалу Чеддока.
При расчетах целесообразно использовать стандартные математические пакеты для персональных компьютеров.
14. Линейное программирование.
14.1. Задача оптимального производства продукции.
Предприятие планирует выпуск двух видов продукции I и II, на производство которых расходуется три вида сырья А, В, и С. Потребность 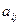 на каждую единицу
на каждую единицу 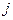 -го вида продукции
-го вида продукции 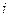 -го вида сырья, запас
-го вида сырья, запас 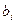 соответствующего вида сырья и прибыль
соответствующего вида сырья и прибыль 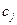 от реализации единицы
от реализации единицы 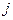 -го вида продукции заданы таблицей:
-го вида продукции заданы таблицей:
| Виды сырья | Виды продукции | Запасы сырья | |
| I | II | ||
| А | 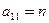
| 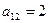
| 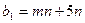
|
| В | 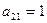
| 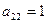
| 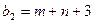
|
| С | 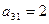
| 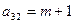
| 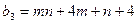
|
| прибыль | 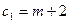
| 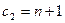
| |
| план (ед.) | 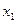
| 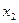
| |
14.1.1. Для производства двух видов продукции I и II с планом 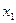 и
и 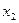 единиц составить целевую функцию прибыли Z и соответствующую систему ограничений по запасам сырья, предполагая, что требуется изготовить в сумме не менее
единиц составить целевую функцию прибыли Z и соответствующую систему ограничений по запасам сырья, предполагая, что требуется изготовить в сумме не менее 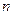 единиц обоих видов продукции.
единиц обоих видов продукции.
14.1.2. В условиях задачи 14.1.1. составить оптимальный план 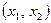 производства продукции, обеспечивающий максимальную прибыль
производства продукции, обеспечивающий максимальную прибыль 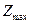 . Определить остатки каждого вида сырья. (Задачу решить симплекс – методом)
. Определить остатки каждого вида сырья. (Задачу решить симплекс – методом)
14.1.3. Построить по полученной системе ограничений многоугольник допустимых решений и найти оптимальный план производства геометрическим путем. Определить соответствующую прибыль 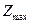 .
.
14.2. Транспортная задача.
На трех складах 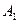 ,
, 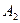 и
и 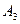 хранится
хранится 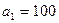 ,
, 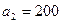 и
и 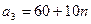 единиц одного и того же груза. Этот груз требуется доставить трем потребителям
единиц одного и того же груза. Этот груз требуется доставить трем потребителям 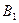 ,
, 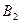 и
и 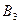 , заказы которых составляют
, заказы которых составляют 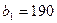 ,
, 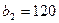 и
и 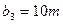 единиц груза соответственно. Стоимость перевозок
единиц груза соответственно. Стоимость перевозок 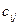 единицы груза с
единицы груза с 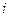 -го склада
-го склада 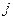 -му потребителю указаны в правых верхних углах соответствующих клеток транспортной таблицы:
-му потребителю указаны в правых верхних углах соответствующих клеток транспортной таблицы:
|
запасы | 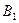
| 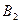
| 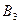
| |
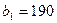
| 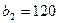
| 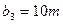
| ||
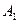
| 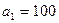
|  4 4
|  2 2
|  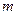
|
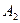
| 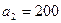
|  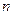
|  5 5
|  3 3
|
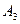
| 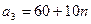
|  1 1
|  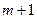
|  6 6
|
14.2.1. Сравнивая суммарный запас 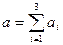 и суммарную потребность
и суммарную потребность 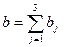 в грузе, установить, является ли модель транспортной задачи, заданная этой таблицей, открытой или закрытой. Если модель является открытой, то ее необходимо закрыть, добавив фиктивный склад
в грузе, установить, является ли модель транспортной задачи, заданная этой таблицей, открытой или закрытой. Если модель является открытой, то ее необходимо закрыть, добавив фиктивный склад 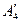 с запасом
с запасом 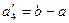 в случае
в случае 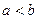 или фиктивного потребителя
или фиктивного потребителя 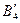 с потребностью
с потребностью 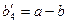 в случае
в случае 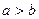 и положив соответствующие им тарифы перевозок нулевыми.
и положив соответствующие им тарифы перевозок нулевыми.
14.2.2. Составить первоначальный план перевозок. (Рекомендуется воспользоваться методом наименьшей стоимости.)
14.2.3. Проверить, является ли первоначальный план оптимальным в смысле суммарной стоимости перевозок, и если это так, то составить оптимальный план
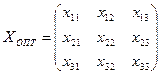 ,
,
обеспечивающий минимальную стоимость перевозок 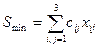 . Найти эту стоимость. (Рекомендуется воспользоваться методом потенциалов.)
. Найти эту стоимость. (Рекомендуется воспользоваться методом потенциалов.)
14.3. Матричные игры.
14.3.1. Игра 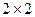 задана матрицей
задана матрицей
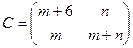
Найти вероятности применения стратегий 1-м и 2-м игроком для получения цены игры. (Задачу решить аналитическим методом.)
14.3.2. Игра задана матрицами
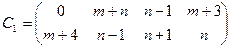 для
для 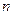 - четного
- четного
и
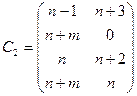 для
для 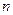 - нечетного.
- нечетного.
Применяя графический метод, найти смешанные оптимальные стратегии обоих игроков и определить цену игры.
15. Математические методы в экономике .
15.1. Сетевое планирование.
Прогресс производства сложной продукции разбивается на отдельные этапы, зашифрованные номерами 1, 2,..., 10. 1 – начальный этап производства продукции, 10 – завершающий. Переход от 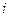 -го этапа к
-го этапа к 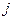 -му этапу назовем операцией. Возможны выполнения операций
-му этапу назовем операцией. Возможны выполнения операций 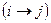 и их продолжительности
и их продолжительности 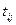 задаются таблицей.
задаются таблицей.
| N п/п | шифр операции | продолжительность операции | 15.1.1. Составьте и упорядочите по слоям сетевой график производства работ. Номера этапов необходимо обвести кружками, а операции |
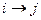
| 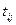
| ||
| 1 | 1→2 | 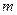
| |
| 2 | 1→3 | 4 | |
| 3 | 1→4 | 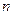
| |
| 4 | 2→3 | 3 | |
| 5 | 2→6 | 5 | |
| 6 | 4→3 | 2 | |
| 7 | 4→6 | 6 | |
| 8 | 3→5 | 3 | 15.1.2. Считая, что начало работы происходит во время |
| 9 | 3→7 | 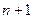
| |
| 10 | 5→9 | 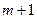
| |
| 11 | 6→7 | 4 | |
| 12 | 6→8 | 3 | |
| 13 | 7→8 | 7 | |
| 14 | 7→9 | 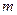
| |
| 15 | 7→10 | 5 | |
| 16 | 8→10 | 4 | |
| 17 | 9→10 | 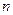
|
15.1.3. Найдите критическое время завершения процесса работ Ткр и выделите стрелки, лежащие на критическом пути.
15.1.4. Для каждой некритической операции 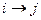 определите резервы свободного времени
определите резервы свободного времени 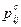 и проставьте их над стрелками рядом с
и проставьте их над стрелками рядом с 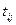 в скобках.
в скобках.
15.1.5. Решите задачу табличным методом. Номера этапов, лежащие на критическом пути подчеркните. (В табличном методе кроме резервов свободного времени 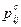 необходимо также найти полные резервы времени
необходимо также найти полные резервы времени 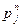 для каждого этапа.)
для каждого этапа.)
Дискретная математика.
Двоичная система счисления.
16.1.1. Записать число 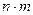 в двоичной системе счисления.
в двоичной системе счисления.
Например: 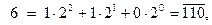
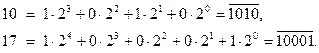
16.1.2. Определить четырехзначное двоичное число 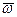 своего задания. Для этого необходимо взять последние 4 цифры полученного в задаче 16.1.1. двоичного числа. Если в нем меньше четырех цифр, то слева нужно дописать нули.
своего задания. Для этого необходимо взять последние 4 цифры полученного в задаче 16.1.1. двоичного числа. Если в нем меньше четырех цифр, то слева нужно дописать нули.
Так: 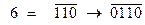 ,
,
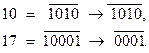
Логика высказываний.
Пусть 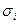 принимает значения 0 либо 1 (
принимает значения 0 либо 1 ( 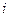 = 1, 2, 3, 4). Положим
= 1, 2, 3, 4). Положим
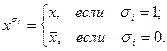
По четырехзначному двоичному числу 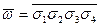 , полученному в задаче 16.1.2, составьте формулу логики высказываний
, полученному в задаче 16.1.2, составьте формулу логики высказываний
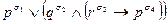
для своего задания. Так, например, двоичному числу 0110 (где 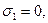
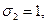
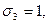
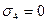 ) соответствует формула
) соответствует формула 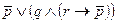 , а двоичному числу 1010 - формула
, а двоичному числу 1010 - формула 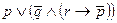 . Для полученной формулы:
. Для полученной формулы:
16.2.1. Найти таблицу истинности.
16.2.2. Определить, эквивалентны ли она и формула 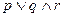 .
.
16.2.3. Найти совершенную дизъюнктивную нормальную форму и совершенную конъюнктивную нормальную форму:
а) табличным методом, б) непосредственным преобразованием.
16.2.4 Составить минимальную релейно-контактную схему, приведя формулу к минимальной дизъюнктивной форме.
Краткое содержание (программа) курса
Линейная алгебра.
Матрицы, действия над ними. Определители, их свойства и вычисление. Обратная матрица. Системы линейных уравнений, условие их совместности. Формулы Крамера, метод Гаусса и матричный способ решения систем. Линейный оператор. Собственные векторы и собственные значения линейных операторов.
Аналитиче c кая геометрия.
Простейшие задачи аналитической геометрии (расстояние между точками, деление отрезка в заданном отношении). Прямая на плоскости, различные виды ее уравнений, угол между прямыми. Расстояние от точки до прямой. Геометрический смысл линейных уравнений и неравенств. Кривые второго порядка, их канонические уравнения.
Векторы, линейные операции над ними. Координаты вектора, его длина, направляющие косинусы. Скалярное, векторное и смешанное произведения векторов, условия их перпендикулярности, коллинеарности, компланарности.
Плоскость в пространстве, ее уравнения, угол между плоскостями, расстояние от точки до плоскости. Прямая в пространстве, ее общие и канонические уравнения. Угол между прямой и плоскостью.
Интегральное исчисление.
Неопределенный интеграл, его основные свойства. Таблица интегралов. Интегрирование подстановкой и по частям. Интегрирование дробно-рациональных, тригонометрических и иррациональных функций.
Интегральная сумма. Определенный интеграл, его геометрический смысл. Свойства определенного интеграла. Формула Ньютона-Лейбница. Интегрирование по частям и замена переменной в определенном интеграле. Несобственные интегралы. Приложения определенного интеграла.
Использование понятия определенного интеграла в экономике.
Элементы теории поля.
Поверхностные интегралы. Поток векторное поля через ориентированную поверхность, его физический смысл. Дивергенция векторного поля, свойства. Теорема Остроградского. Линейный интеграл. Циркуляция векторного поля. Ротор (вихрь) векторного поля, свойства ротора. Теорема Стокса. Потенциальное поле. Потенциал. Соленоидальное поле.
Ряды.
Числовые ряды, сходимость и сумма ряда. Необходимое условие сходимости. Свойства сходящихся рядов. Достаточные признаки сходимости рядов с неотрицательными членами (признаки сравнения, Даламбера, Гаусса, радикальный признак Коши, интегральный признак). Знакочередующиеся ряды. Признак Лейбница. Знакопеременные ряды. Абсолютно и условно сходящиеся ряды. Функциональные ряды, область сходимости, методы её определения.Степенные ряды, действия над ними. Теорема Абеля о сходимости степенных рядов. Формулы для вычисления радиуса сходимости степенных рядов. Ряды Тейлора и Маклорена. Разложение функций у = s in x, c os x, ex, (1+x)m, ln (1+x), arctg x в степенные ряды. Применение степенных рядов в приближенных вычислениях (приближенное вычисление значений функций, определенных интегралов, приближенное решение дифференциальных уравнений). Тригонометрические ряды Фурье. Разложение функций в тригонометрические ряды Фурье.
Операционное исчисление.
Начальная функция (оригинал) и ее изображение. Теорема о существовании изображения. Теорема единственности оригинала. Свойство линейности изображения. Таблица оригиналов и изображений изображений некоторых функций. Теорема подобия. Теорема смещения. Теорема запаздывания. Теорема свертывания. Дифференцирование оригиналов. Интегрирование оригиналов. Таблица оригиналов и их изображений. Интегрирование линейных дифференциальных уравнений с постоянными коэффициентами.
Теория вероятностей.
Случайные события, алгебра событий. Относительная частота, статистическое определение вероятности. Классическое определение вероятности. Геометрическое определение вероятности, задача о встрече. Формулы комбинаторики. Теоремы сложения. Независимые события, теоремы умножения. Формула полной вероятности. Формулы Байеса. Повторение испытаний. Формула Бернулли. Наивероятнейшее число событий. Локальная и интегральная теоремы Лапласа. Случайные величины. Функция распределения (интегральный закон распределения). Плотность распределения (дифференциальный закон распределения). Математическое ожидание, его свойства. Дисперсия, ее свойства, среднее квадратическое отклонение. Основные примеры распределений случайных величин (биномиальное, геометрическое, гипергеометрическое, Пуассона, равномерное, показательное, нормальное). Вероятность попадания в заданный интервал нормально распределенной случайной величины Оценка отклонения теоретического распределения от нормального. Асимметрия и эксцесс. Распределения, связанные с нормальным. Многомерные случайные величины. Числовые характеристики системы случайных величин. Коэффициент корреляции. Законы больших чисел. Предельные теоремы.
Математическая статистика.
Выборочный метод, статистическое распределение. Эмпирическая функция распределения. Полигон и гистограмма. Оценка параметров, свойства точечных оценок. Условные варианты, метод произведений. Доверительный интервал. Метод наибольшего правдоподобия. Статистическая проверка статистических гипотез. Критерии согласия. Метод наименьших квадратов. Уравнение прямой линии регрессии. Выборочный коэффициент корреляции.
Линейное программирование.
Общая и основная задачи линейного программирования (ЛП). Основные теоремы ЛП. Геометрический метод решения задач ЛП. Симплек-метод: определение первоначального допустимого базисного решения; проверка решения на оптимальность; переход к другому допустимому решению. Двойственные задачи: их свойства; теоремы двойственности; объективно обусловленные оценки и их смысл. Транспортная задача: экономико-математическая модель транспортной задачи; нахождение первоначального базисного распределения поставок (метод «северо-западного» угла, метод наименьших затрат); критерий оптимальности базисного распределения поставок; перераспределение поставок; вырождение транспортной задачи; открытая модель транспортной задачи. Элементы теории игр: основные понятия; антагонистические игры, платежная матрица; решение игр в смешанных стратегиях; геометрические решения игр размера 2xn, mx2; приведение матричной игры к задаче ЛП.
Дискретная математика.
Высказывания, логические операции над ними. Равносильность формул логики высказываний. Алгебра Буля. Представление булевой функции формулой логики высказываний. Закон двойственности. Нормальные и совершенные нормальные формы формул. Предикаты, логические операции над ними. Кванторные операции. Формулы логики предикатов, их равносильность, нормальная форма. Комбинаторные схемы. Основные понятия и определения теории графов. Изоморфизм. Матричное задание графов. Операции над графами. Кратчайший путь между вершинами. Алгоритм Дейкстры. Поток в транспортной сети. Теорема Форда-Фалкерсона. Задача о максимальном потоке. Алгоритм Форда-Фалкерсона.
Список учебной литературы
1. И.Л.Акулич. Математическое программирование в примерах и задачах.—М.: Высшая школа, 1986.
2. И.П.Алдохин. Теория массового обслуживания в промышленности.— М.: Экономика,1980.
3. Я.С.Бугров, С.М.Никольский. Дифференциальное и интегральное исчисления.—М.: Наука, 1990.
4. Я.С.Бугров, С.М.Никольский. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного.— М: Наука, 1988.
5. Я.С.Бугров, С.М.Никольский. Элементы линейной алгебры и аналитической геометрии.—М.: Наука, 1990.
6. Е.С.Вентцель. Прикладные задачи теории вероятностей.—М.:Наука,1984.
7. В.Е.Гмурман. Курс теории вероятностей и математической статистики.—М.: Высшая школа, 1980.
8. В.Е.Гмурман. Руководство к решению задач по теории вероятностей и математической статистике.—М.: Высшая школа, 1980.
9. П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах. Том 1,2.—М.: Высшая школа, 2000.
10. Н.В.Ефимов. Краткий курс аналитической геометрии.—М.: Наука, 1980.
11. В.А.Ильин, Э.Г.Позняк. Линейная алгебра.—М.: Наука, 1974.
12. М.Л.Краснов, А.И.Киселев, Г.Н. Макаренко. Функции комплексного переменного. Операционное исчисление. Теория устойчивости.— М.: Наука, 1981.
13. Ю.Н.Кузнецов, В.И.Кузубов, А.Б.Велощенко. Математическое программирование.—М.: Высшая школа, 1980.
14. А.И.Ларионов, Т.И.Юрченко, А.Л.Новоселов. Экономико—математические методы-—М.: Высшая школа, 1991.
15. Н.С.Пискунов. Дифференциальное и интегральное исчисления Том 1,2.— М.: Наука, 1988.
16. П.Н.Романовский. Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа.—М.: Наука, 1986.
17. А.Г.Свешников, А.Н.Тихонов. Теория функций комплексного переменного.—М.: Наука, 1984.
18. Л.Л.Терехов. Экономико—математические методы.—М.: Статистика, 1982.
СБОРНИК ЗАДАНИЙ
ПО МАТЕМАТИКЕ
Контрольные задания и программа по курсам математики и математических методов в экономике
для студентов заочного отделения
Санкт-Петербург
2005
Утверждены Методическим Советом СПбГАСЭ
Сборник заданий по математике. Контрольные задания и программа по курсам математики и математических методов в экономике для студентов заочного отделения. - СПб.: Изд-во СПбГАСЭ, 2005. – 32 с.
Сборник содержит задачи для контрольных работ по всем курсам математических дисциплин, предусмотренным учебными планами специальностей, и краткий перечень вопросов для подготовки к экзаменам.
Каждая контрольная работа состоит из задач одного или нескольких разделов данного сборника, выбранных в соответствии с рабочей программой.
Перечень разделов сборника, необходимых для выполнения контрольных работ по каждой специальности, сообщается студентам этой специальности в начале семестра.
Составители: канд. физ.-мат. наук, проф. С.И.Никитин;
канд. физ.-мат. наук, доц. А.Л.Пирозерский;
канд. физ.-мат. наук, доц. Н.Ю.Кропачева;
старший преподаватель М.Ю.Никанорова.
© Санкт-Петербургская государственная академия сервиса и экономики
2005 г.
Содержание
Требования к оформлению контрольных работ ...................................... 4
Формирование исходных данных к задачам ............................................ 4
Раздел 1. Линейная алгебра .................….............................................. 5
Раздел 2. Аналитическая геометрия ...................................................... 6
Раздел 3. Дифференциальное исчисление............................................. 7
Раздел 4. Интегральное исчисление ...................................................... 8
Раздел 5. Функции нескольких переменных ........................................ 9
Раздел 6. Двойные, тройные и криволинейные интегралы ................. 9
Раздел 7. Элементы теории поля ........................................................... 10
Раздел 8. Дифференциальные уравнения .............................................. 11
Раздел 9. Ряды .......................................................................................... 12
Раздел 10. Функции комплексного переменного ................................... 13
Раздел 11. Операционное исчисление ..................................................... 14
Раздел 12. Теория вероятностей .............................................................. 15
Раздел 13. Математическая статистика .................................................. 16
Раздел 14. Линейное программирование ................................................ 18
Раздел 15. Математические методы в экономике .................................. 21
Раздел 16. Дискретная математика .......................................................... 23
Краткое содержание (программа) курса.................................................... 25
Список учебной литературы ...................................................................... 31
Требования к оформлению контрольных работ
1. Контрольные работы следует выполнять в ученических тетрадях в клетку. На обложке необходимо указать: название института Академии; название кафедры (математики и математических методов в экономике); название и номер контрольной работы; название (номер) специальности; фамилию, имя, отчество и личный шифр студента.
2. На каждой странице надо оставить поля размером 4 см для оценки решения задач и методических указаний проверяющего работу.
3. Условия задач переписывать полностью необязательно, достаточно указать номер задачи по данному сборнику. В условия задач надо сначала подставить конкретные числовые значения параметров т и п, и только после этого приступать к их решению.
4. Задачи в контрольной работе нужно располагать в порядке возрастания номеров.
Формирование исходных данных к задачам
Каждая контрольная работа состоит из задач одного или нескольких разделов сборника.
Условия задач, входящих в контрольную работу, одинаковы для всех студентов, однако числовые данные задач зависят от личного шифра студента, выполняющего работу.
Числовых данных параметров т и п определяются по двум последним цифрам своего шифра (А — предпоследняя цифра, В — последняя цифра). Значение параметра т выбирается из таблицы 1, а значение параметра п - из таблицы 2. Эти два числа т и п и нужно подставить в условия задач контрольной работы.
Таблица 1 (выбор параметра т)
| А | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| т | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Таблица 2 (выбор параметра п )
| В | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| п | 5 | 3 | 2 | 4 | 1 | 4 | 5 | 2 | 3 | 1 |
Например, если шифр студента 1604 — 037, то А = 3, В = 7, и из таблиц находим, что т = 4, п = 2. Полученные т = 4 и п = 2 подставляются в условия всех задач контрольной работы этого студента.
Линейная алгебра
Действия с матрицами.
Выполнить действия:
а) 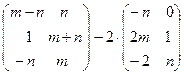 ; б)
; б) 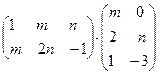 .
.
Вычисление определителей.
Вычислить определитель 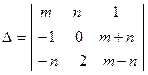 двумя способами:
двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
Обратная матрица.
Найти обратную матрицу к матрице 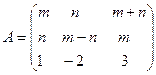 и проверить выполнение равенства
и проверить выполнение равенства 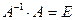 .
.
Системы линейных уравнений.
Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) с помощью вычисления обратной матрицы, записав систему в матричном виде 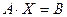 :
:
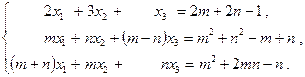
Дата: 2018-12-28, просмотров: 330.
 потребности
потребности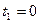 , определите время
, определите время 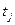 окончания каждого
окончания каждого