 Совокупность n дифференциальных уравнений вида
Совокупность n дифференциальных уравнений вида
х'1 + а11х1 + а12х2 + … + а1nхn = f1(t),
x'2 + а21x1 + а22x2 + … + а2nxn = f2(t),
— — — — — — — — — — — —
x'n + аn1x1 + аn2x2 + … + а nn xn = fn(t).
где t – аргумент, x1, x2, …, xn – неизвестные функции, называется системой линейных дифференциальных уравнений первого порядка с постоянными коэффициентами.
Проинтегрировать эту систему, значит найти ее решение, т.е. систему функций x1(t), x2(t), …, xn(t), обращающих равенства в тождества.
Пример выполнения задания 3
Решим систему 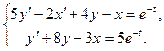
Решение.
Данную систему решим методом исключения.
Исключаем х из данных уравнений. Из второго уравнения имеем:
х = 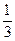 (у' + 8у – 5е-t).
(у' + 8у – 5е-t).
Продифференцируем его по аргументу t:
х' = 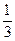 (у'' + 8у' + 5е-t), и подставим в первое уравнение. После упрощения получим:
(у'' + 8у' + 5е-t), и подставим в первое уравнение. После упрощения получим:
у'' + у' – 2у = -4е-t (*).
Это линейное дифференциальное уравнение. Найдем его общее решение у = у0 + ỹ .
Корни характеристического уравнения k2 + k – 2 = 0
k1 = 1, k2 = -2.
Общее решение однородного уравнения у0 = С1еt + C2e-2t.
Частное решение неоднородного уравнения (*) ищем в виде
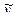 = А e-t.
= А e-t.
Найдем 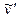 = -А е-t,
= -А е-t, 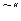 = А е-t и подставим в уравнение (*). Получим А = 2, следовательно,
= А е-t и подставим в уравнение (*). Получим А = 2, следовательно, 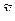 =2e-t.
=2e-t.
у = С1et + C2e-2t + 2e-t. Определим х, пользуясь равенством
х = 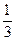 (у' + 8у – 5е-t). Найдем у' = C1et – 2C2e-2t – 2e-t .
(у' + 8у – 5е-t). Найдем у' = C1et – 2C2e-2t – 2e-t .
После подстановки у и у' :
х = 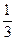 (C1et – 2C2e-2t – 2e-t + 8(C1et + C2e-2t + 2e-t) – 5e-t).
(C1et – 2C2e-2t – 2e-t + 8(C1et + C2e-2t + 2e-t) – 5e-t).
Упростив, получим х = 3С1et + 2e-2t + 3e-t.
 Общим решением данной системы будут функции:
Общим решением данной системы будут функции:
х = 3С1et + 2e-2t + 3e-t,
у = С1еt + C2e-2t + 2e-t.
Модуль 8
Ряды
Задачи для решения
Задание 1
Исследовать на сходимость числовые ряды.
Варианты
- а)
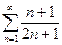 ; б)
; б) 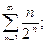
в) 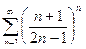 ; г)
; г) 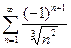 .
.
2. а) 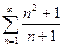 ; б)
; б) 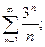
в) 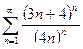 ; г)
; г) 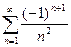 .
.
3. а) 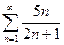 ; б)
; б) 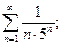
в) 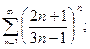 г)
г) 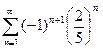 .
.
4. а) 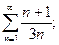 б)
б) 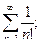
в) 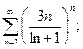 г)
г) 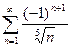 .
.
5. а) 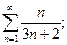 б)
б) 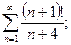
в) 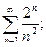 г)
г) 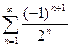 .
.
6. а) 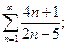 б)
б) 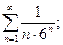
в) 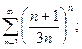 г)
г) 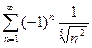 .
.
7. а) 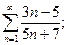 б)
б) 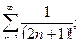
в) 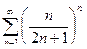 ; г)
; г) 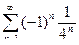 .
.
8. а) 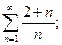 б)
б) 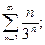
в) 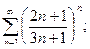 г)
г) 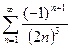 .
.
9. а) 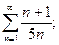 б)
б) 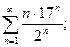
в) 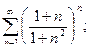 г)
г) 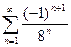 .
.
10. а) 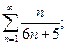 б)
б) 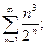
в) 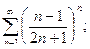 г)
г) 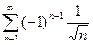 .
.
Задание 2
Определить радиус и область сходимости степенных рядов.
Варианты
1. а) 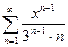 ; б)
; б) 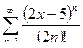 .
.
2. а) 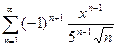 ; б)
; б) 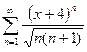 .
.
3. а) 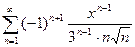 ; б)
; б) 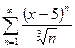 .
.
4. а) 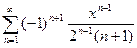 ; б)
; б) 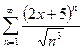 .
.
5. а) 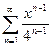 ; б)
; б) 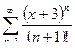 .
.
6. а) 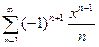 ; б)
; б) 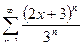 .
.
7. а) 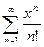 ; б)
; б) 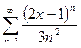 .
.
8. а) 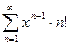 ; б)
; б) 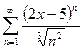 .
.
9. а) 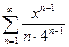 ; б)
; б) 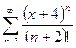 .
.
10. а) 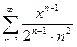 ; б)
; б) 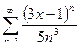 .
.
Задание 3
Разложить заданную функцию в ряд Фурье в интервале [-π; π].
Варианты
1. a) 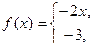
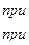
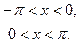
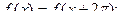
б) f(x) = 2x на отрезке [0;2] по косинусам.
2. a) 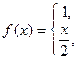
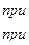
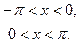
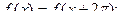
б) f(x) = 1 – x на отрезке [0;1] по синусам.
3. a) 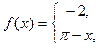
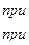
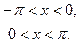
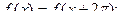
б) 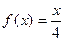 на отрезке [0;4] по косинусам.
на отрезке [0;4] по косинусам.
4. a) 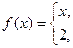
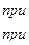
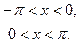
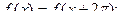
б) f(x) = x – 1 на отрезке [0;1] по косинусам.
5. a) 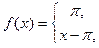
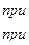
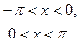
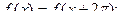
б) f(x) = 2 – 2x на отрезке [0;1] по синусам.
6. а) 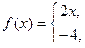
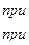
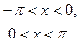
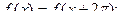
б) 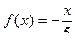 на отрезке [-5;0] по косинусам.
на отрезке [-5;0] по косинусам.
7. а) 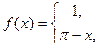
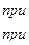
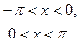
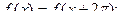
б) f(x) = 3 – x, на отрезке [0;3] по синусам.
8. а) 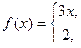
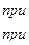
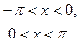
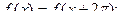
б) f(x) = 1 – 2x на отрезке [0;1/2] по косинусам.
9. а) 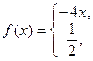
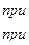
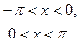
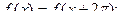
б) f(x) = -2x на отрезке [0;1/2] по синусам.
10. а) 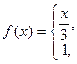
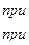
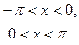
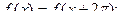
б) 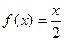 на отрезке [0;4] по косинусам.
на отрезке [0;4] по косинусам.
Решение типовых задач
Задание 1
Исследовать на сходимость числовые ряды.
а) 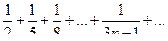 ;
;
б) 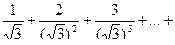
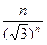 +…;
+…;
в) 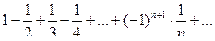 .
.
Задание 2
Определить радиус и область сходимости степенного ряда 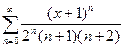 .
.
Задание 3
Разложить функцию 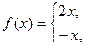
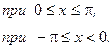 в ряд Фурье в интервале [-π; π].
в ряд Фурье в интервале [-π; π].
Решение типовых задач
Сведения из теории
Числовые ряды
Числовым рядом называют сумму бесконечной числовой последовательности вида
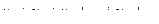 =
= 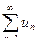 .
.
Числа 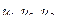 называют членами ряда, un – общим членом ряда.
называют членами ряда, un – общим членом ряда.
Конечная сумма Sn = 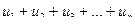 называется n-ойчастичной суммой ряда.
называется n-ойчастичной суммой ряда.
Если существует конечный предел 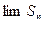 , ряд называется сходящимся, в противном случае – расходящимся.
, ряд называется сходящимся, в противном случае – расходящимся.
Необходимый признак сходимости
Если ряд сходится, то его общий член un стремится к нулю при n → ∞, т.е. 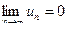 .
.
Указанный признак не является достаточным, т.е. если un → 0, то о сходимости ряда ничего сказать нельзя.
Достаточные признаки
Признак сравнения
Если даны два ряда
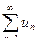 и
и 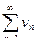 с положительными членами, причем члены первого ряда не превосходят соответствующих членов второго ряда: 0 ≤ un ≤ vn , то
с положительными членами, причем члены первого ряда не превосходят соответствующих членов второго ряда: 0 ≤ un ≤ vn , то
а) из сходимости второго ряда следует сходимость первого ряда;
б) из расходимости первого ряда следует расходимость второго ряда.
Для сравнения часто используются ряды:
Ряд геометрической прогрессии:
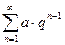
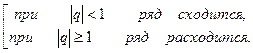
Обобщенно-гармонический ряд:
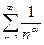
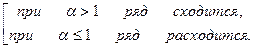
Предельный признак сравнения
Если даны два ряда
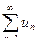 и
и 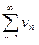 с положительными членами и существует конечный предел
с положительными членами и существует конечный предел 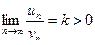 , то рассматриваемые ряды одновременно сходятся или расходятся.
, то рассматриваемые ряды одновременно сходятся или расходятся.
Признак Даламбера
Если ряд 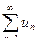 с положительными членами таков, что существует предел
с положительными членами таков, что существует предел
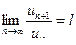 , то
, то 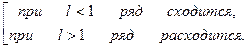
Радикальный признак Коши
Если ряд 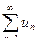 с положительными членами таков, что существует предел
с положительными членами таков, что существует предел
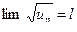 , то
, то 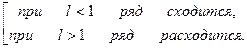
Интегральный признак Коши
Если функция f(x) непрерывная, положительная и невозрастающая для x ≥ a и, начиная с некоторого n= N,
un = f(n), то ряд 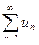 и несобственный интеграл
и несобственный интеграл 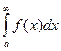 одновременно сходятся или расходятся.
одновременно сходятся или расходятся.
Признак Лейбница о сходимости знакочередующихся рядов
Ряд u1 – u2 + u3 - … + (-1)n+1 un + …, где все un > 0, называется знакочередующимися.
Если члены знакочередующегося ряда удовлетворяют условиям
u1 > u2 > u3 > … > un , и 
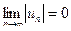 , то такой ряд сходится.
, то такой ряд сходится.
Если ряд 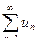 сходится, а ряд
сходится, а ряд 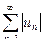 расходится, то такой ряд называют условно сходящимся.
расходится, то такой ряд называют условно сходящимся.
Если ряд 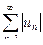 сходится, то сходится и ряд
сходится, то сходится и ряд 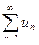 , который в этом случае называют абсолютно сходящимся.
, который в этом случае называют абсолютно сходящимся.
Степенные ряды
Степенным рядом называется ряд вида
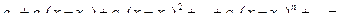
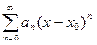 ,
,
где an – числа, коэффициенты степенного ряда.
При х0 = 0 степенной ряд имеет вид:
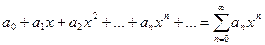 .
.
Значения х, при которых степенной ряд является сходящимся числовым рядом, образуют область сходимости ряда.
Об области сходимости степенного ряда можно судить, исходя из теоремы:
Если степенной ряд сходится при х = х0 ≠ 0, то он абсолютно сходится при всех значениях х, удовлетворяющих неравенству |x| < |x0|.
Число R называется радиусом сходимости степенного ряда, его находят по формуле: 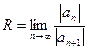 .
.
Пример выполнения задания 1
Исследуем на сходимость числовые ряды.
а) 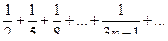 .
.
Общий член ряда 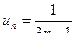 и
и 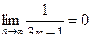 . Сравним данный ряд с гармоническим рядом
. Сравним данный ряд с гармоническим рядом 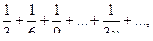 являющимся расходящимся. Так как
являющимся расходящимся. Так как 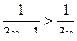 , то исходный ряд по признаку сравнения расходится.
, то исходный ряд по признаку сравнения расходится.
б) 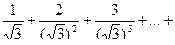
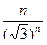 +… .
+… .
Общий член ряда 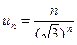 и его предел
и его предел
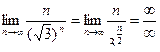 .
.
Применим правило Лопиталя: 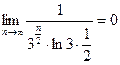 .
.
Необходимый признак сходимости выполняется.
Воспользуемся признаком Даламбера:
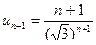 ;
; 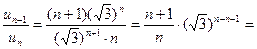
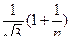 ,
,
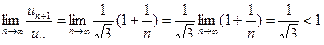 .
.
Следовательно, ряд сходится.
в) 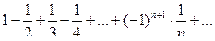 .
.
Это знакочередующийся ряд с общим членом 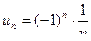 .
.
Воспользуемся признаком Лейбница:
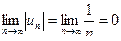 и
и 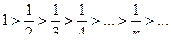 .
.
Следовательно, ряд сходится.
Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:
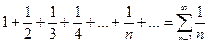 .
.
Это гармонический ряд. Он расходится. Значит, данный ряд сходится условно.
Пример выполнения задания 2
Определить радиус и область сходимости степенного ряда
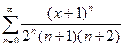 .
.
Решение.
Обозначим х + 1 = Х и рассмотрим ряд
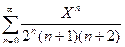 . Определим его радиус сходимости
. Определим его радиус сходимости
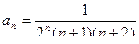 ,
, 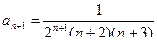 ,
,
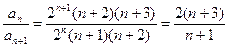 .
.
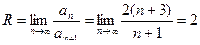 , значит, для всех |Х| < 2 ряд сходится.
, значит, для всех |Х| < 2 ряд сходится.
Решением неравенства является интервал (-2,2).
Рассмотрим поведение ряда на концах полученного интервала
При Х = -2 имеем
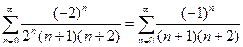 - ряд знакочередующийся.
- ряд знакочередующийся.
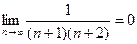 и
и 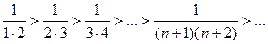 Следовательно, по признаку Лейбница ряд сходится.
Следовательно, по признаку Лейбница ряд сходится.
При Х = 2 имеем:
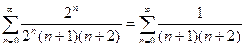 .
.
Сравним его с обобщенно-гармоническим рядом 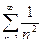 .
.
Он является сходящимся.
Так как 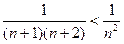 , то данный ряд сходится.
, то данный ряд сходится.
Степенной ряд сходится на обоих концах интервала сходимости.
-2 ≤ Х ≤ 2 ,
-2 ≤ x + 1 ≤ 2,
-3 ≤ x ≤ 1.
Таким образом, областью сходимости данного ряда является интервал вида х 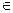 [-3;1].
[-3;1].
Сведения из теории
Ряды Фурье
Пусть f(x) – какая-нибудь функция с периодом 2π. Рядом Фурье функции f(x) называется тригонометрический ряд
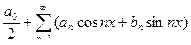 , коэффициенты которого определяются по формулам Фурье:
, коэффициенты которого определяются по формулам Фурье:
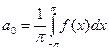 ;
; 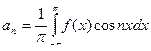 , n = 1,2,3,…;
, n = 1,2,3,…;
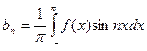 , n = 1,2,3,….
, n = 1,2,3,….
Из этого определения не следует, что f(x) всегда разлагается в свой ряд Фурье.
Функция f(x) удовлетворяет условиям Дирихле на отрезке
[-π; π], если:
1) она имеет конечное число экстремумов на [-π; π];
2) она на этом отрезке непрерывна, за исключением конечного числа точек разрыва 1-го рода;
3) существуют конечные предельные значения функции
f(-π + 0) и f(π - 0).
Теорема Дирихле: если функция f(x) на отрезке [-π; π] удовлетворяет условиям Дирихле, то ряд Фурье функции f(x) сходится для всех х, а его сумма равна значению f(x) в каждой точке непрерывности этой функции, и равна числу 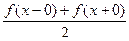 в каждой точке разрыва.
в каждой точке разрыва.
Если функция f(x) задана на отрезке [-l;l], где l – произвольное число, причём f(x + 2l) = f(x), и она удовлетворяет условиям Дирихле, то функция может быть разложена в ряд Фурье:
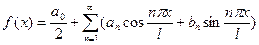 , где
, где
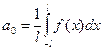 ;
; 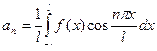 , n = 1,2,3,…;
, n = 1,2,3,…;
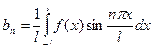 , n = 1,2,3,….
, n = 1,2,3,….
Если функция f(x) чётная, т.е. f(-x) = f(x), то 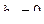 ,
,
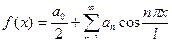 ;
;
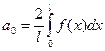 ;
; 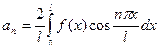 .
.
Если функция f(x) нечётная, т.е. f(-x) = -f(x), то  ,
,
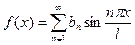 ;
;
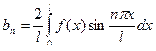 .
.
Пример выполнения задания 3
Разложим в ряд Фурье функцию f(x) периода 2π, заданную на отрезке [-π; π] формулой
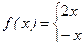
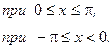
Эта функция удовлетворяет условиям Дирихле, значит, её можно разложить в ряд Фурье. Находим коэффициенты ряда:
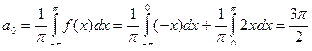 ;
;
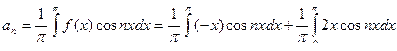 ,
,
интегрируя по частям, получим:
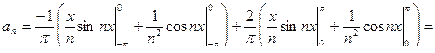
= 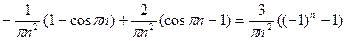 .
.
Аналогично находим
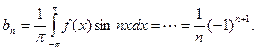
Исходной функции f(x) соответствует ряд Фурье
f(x)= 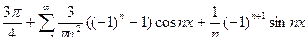 .
.
I V семестр
Вопросы
1. Непрерывное преобразование Лапласа. Оригинал и
изображение.
- Таблица оригиналов и изображений.
- Свойства преобразования Лапласа.
- Дифференцирование и интегрирование оригинала.
- Дифференцирование и интегрирование изображения.
- Метод операционного исчисления при решении дифференциальных уравнений и их систем.
- Случайные события. Классификация событий.
- Вероятность события. Основные определения вероятности события.
- Сумма и произведение событий.
- Условная вероятность
- Теоремы сложения вероятностей.
- Формула полной вероятности.
- Формула Байеса.
- Последовательность независимых испытаний. Формула Бернулли.
- Формула Пуассона.
- Формула Муавра-Лапласа.
- Дискретные и непрерывные случайные величины. Закон распределения.
- Функция распределения. Её свойства.
- Числовые характеристики дискретной случайной величины. Их свойства.
- Числовые характеристики непрерывной случайной величины. Их свойства.
- Биноминальное распределение.
- Пуассоновское распределение.
- Равномерное распределение.
- Показательное распределение.
- Нормальное распределение.
- Вероятность попадания случайной величины на заданный участок.
Модуль 9
Операционное исчисление
Задачи для решения
Задание 1
Пользуясь преобразованием Лапласа и основными его свойствами, найти изображения функций:
1. 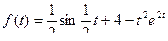 ;
;
2. 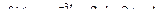 ;
;
3. 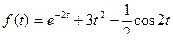 ;
;
4.  ;
;
5. 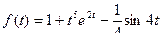 ;
;
6.  ;
;
7. 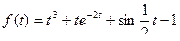 ;
;
8. 
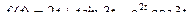 ;
;
9. 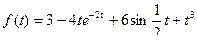 ;
;
10. 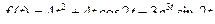 .
.
Задание 2
По известному изображению F(p) найти оригинал 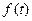
1. 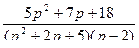 ;
;
2. 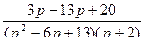 ;
;
3. 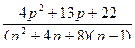 ;
;
4. 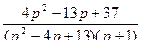 ;
;
5. 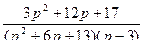 ;
;
6. 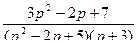 ;
;
7. 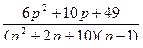 ;
;
8. 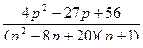 ;
;
9. 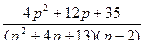 ;
;
10. 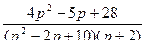 ;
;
Задание 3
Методами операционного исчисления найти решение дифференциального уравнения, удовлетворяющее начальным условиям.
1. 
2. 
3. 
4. 
5. 
6. 
7. 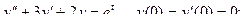
8. 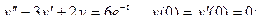
9. 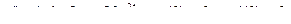
10. 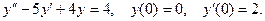
Задание 4.
Решить систему дифференциальных уравнений при заданных начальных условиях.
1. 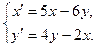
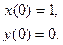
2. 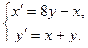
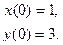
3. 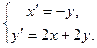
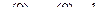 .
.
4. 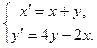
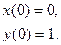
5. 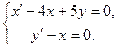
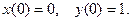
6. 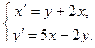

7. 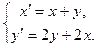
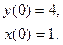
8. 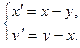
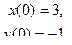
9. 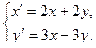
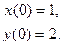
10. 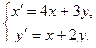
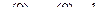 .
.
Решение типовых задач
Задание 1
Пользуясь преобразованием Лапласа и основными его свойствами, найти изображения функции
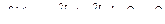 .
.
Задание 2
По известному изображению F(p) найти оригинал 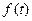 .
.
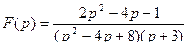 .
.
Задание 3
Методами операционного исчисления найти решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.
 .
.
Задание 4
Решить систему дифференциальных уравнений при заданных начальных условиях.
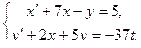
Начальные условия: 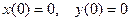 .
.
Сведения из теории
Функцией – оригиналом называют функцию 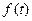 действительного аргумента
действительного аргумента 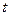 , удовлетворяющую условиям:
, удовлетворяющую условиям:
1. для всех отрицательных значений аргумента функция тождественно равна нулю, т.е. 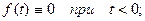
2. функция 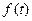
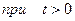 возрастает не быстрее показательной функции, т.е. существуют такие постоянные
возрастает не быстрее показательной функции, т.е. существуют такие постоянные 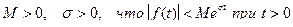 ;
;
3. на любом конечном отрезке  положительной полуоси
положительной полуоси 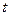 эта функция удовлетворяет условиям Дирихле:
эта функция удовлетворяет условиям Дирихле:
- ограничена;
- непрерывна или имеет конечное число точек разрыва
первого рода;
- имеет конечное число экстремумов.
Изображением функции 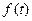 по Лапласу (преобразованием по Лапласу ) называют функцию комплексной переменной
по Лапласу (преобразованием по Лапласу ) называют функцию комплексной переменной  определяемую соотношением
определяемую соотношением 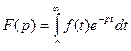 .
.
Интеграл в правой части называется интегралом Лапласа.
Функция  определяется в полуплоскости
определяется в полуплоскости 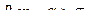 и является в этой области аналитической функцией.
и является в этой области аналитической функцией.
Функция комплексной переменной  является изображением по Лапласу функции действительного аргумента
является изображением по Лапласу функции действительного аргумента 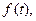 обозначатся
обозначатся
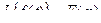 или
или 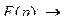
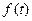 .
.
Свойства преобразования Лапласа
Линейность
Если 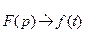
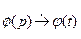 , то
, то 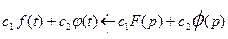 .
.
Т.е. сумма нескольких функций, умноженных на постоянные, равна сумме изображений этих функций, умноженных на соответствующие постоянные.
Подобие
Если 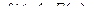 то
то 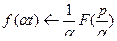 .
.
Т.е. умножение аргумента оригинала на положительное число 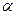 приводит к делению аргумента изображения и самого изображения на тоже число.
приводит к делению аргумента изображения и самого изображения на тоже число.
Запаздывание (оригинала)
Если 
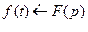 и
и  то
то  .
. 
Т.е. запаздывание оригинала на время 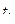 соответствует умножение изображения на
соответствует умножение изображения на 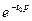 .
.
Смещение (изображения)
Если 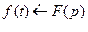 , то
, то  .
.
Т.е. умножение оригинала на множитель 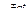 приводит к изменению аргумента изображения на величину
приводит к изменению аргумента изображения на величину 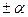 .
.
Дифференцирование оригинала
Если функция 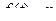 раз непрерывно дифференцируемая на промежутке
раз непрерывно дифференцируемая на промежутке 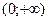 функция и
функция и 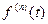 является оригиналом, то из соответствия
является оригиналом, то из соответствия  следует
следует 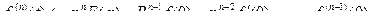 .
.
Дифференцирование изображения
Если 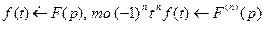 .
.
Свертка оригиналов (умножение изображений).
Если  ,
,  -показатели роста функции
-показатели роста функции 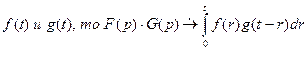 .
.
Т.е. свертывание функций в пространстве оригиналов соответствует умножению функций в пространстве изображений.
Таблица оригиналов и изображений
| № | 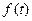
| 
|
| 1. | 1 | 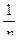
|
| 2. | 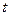
| 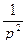
|
| 3. | 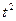
| 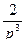
|
| 4. | 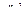
| 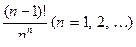
|
| 5. | 
| 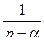
|
| 6. | 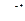
| 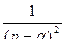
|
| 7. | 
| 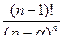
|
| 8. | 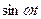
| 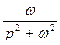
|
| 9. | 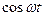
| 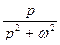
|
| 10. | 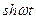
| 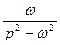
|
| 11. | 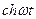
| 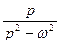
|
| 12. | 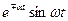
| 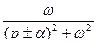
|
| 13. | 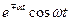
| 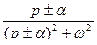
|
| 14. | 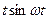
| 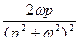
|
| 15. | 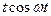
| 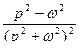
|
Пример выполнения задания 1
Пользуясь преобразованием Лапласа и основными свойствами преобразования Лапласа, найдём изображение функции
 .
.
Решение
Используя свойства линейности, подобия, теорему дифференцирования изображения, найдем изображения функций:
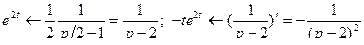 ;
;
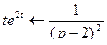 .
.
Воспользуемся формулой таблицы оригиналов и изображений:
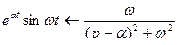 ,
, 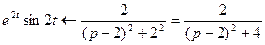 ,
, 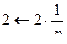 .
.
Получаем: 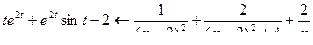 .
.
Пример выполнения задания 2
По известному изображению 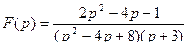
найдём функцию-оригинал.
Решение.
Для нахождения оригинала 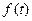 представим его изображение
представим его изображение 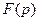 в виде суммы простейших рациональных дробей с неопределенными коэффициентами.
в виде суммы простейших рациональных дробей с неопределенными коэффициентами.
Разложение 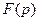 имеет вид:
имеет вид:
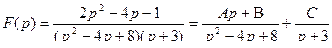 .
.
Неопределенные коэффициенты найдем из тождества
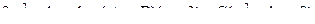
Приравняем коэффициенты слева и справа при одинаковых степенях 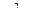 и
и 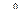 .
.
Получим систему: 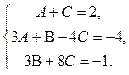
Решая данную систему, получим 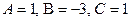 .
.
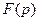 примет вид:
примет вид:
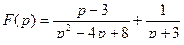 .
.
Преобразуем первое слагаемое, выделив в знаменателе полный квадрат суммы
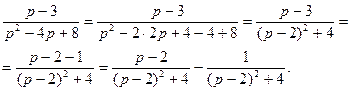
Из таблицы преобразований Лапласа, применяя свойство линейности, имеем 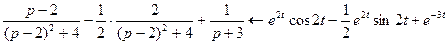
Пример выполнения задания 3
Решим операторным методом линейное дифференциальное уравнение при заданных начальных условиях.
 .
.
Решение.
Найдем операторное уравнение. Применим преобразование Лапласа к обеим частям заданного уравнения.
По теореме о дифференцировании имеем: если  , то
, то
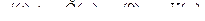 ,
,
 ,
,
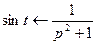 .
.
После подстановки полученных изображений в исходное уравнение, получим операторное уравнение 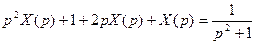 .
.
После преобразований: 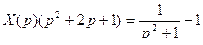 ,
,
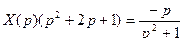 .
.
Разрешая это операторное уравнение относительно  , получим:
, получим: 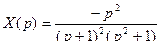 .
.
Это и есть изображение искомого решения 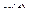 .
.
Для нахождения оригинала 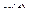 представим его изображение
представим его изображение  в виде дробей и вводя неопределенные коэффициенты, получаем:
в виде дробей и вводя неопределенные коэффициенты, получаем:
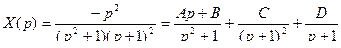 .
.
Неопределенные коэффициенты найдем из тождества
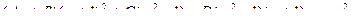 .
.
Пусть 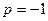 , тогда
, тогда 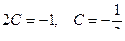 .
.
Приравняем коэффициенты слева и справа при одинаковых степенях 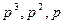 и свободных членах:
и свободных членах:
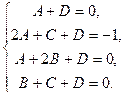
Решая данную систему, получим 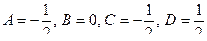 .
.
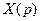 примет вид:
примет вид: 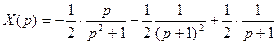 .
.
Применив соответствующие формулы таблицы оригиналов и изображений, получим 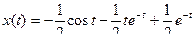 , или
, или 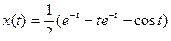 - это решение заданного уравнения.
- это решение заданного уравнения.
Пример выполнения задания 4
Решим систему дифференциальных уравнений
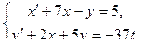
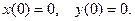
Решение.
Пусть 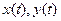 составляют искомое решение и пусть
составляют искомое решение и пусть 
Применяя прямое преобразование Лапласа, получим операторные уравнения, системы дифференциальных уравнений.
 ,
,
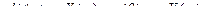 ,
,
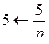 ,
, 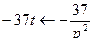 .
.
Система дифференциальных уравнений обращается в систему операторных уравнений:
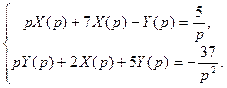
или 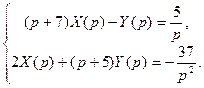
Решаем данную систему по формулам Крамера относительно изображений 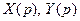 :
:
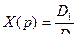 ,
, 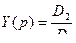 .
.
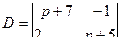
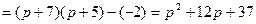 ,
,
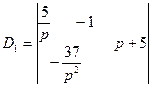
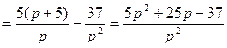 ,
,
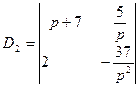
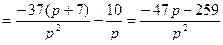 .
.
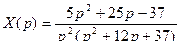 ,
,
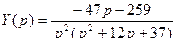 .
.
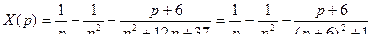 ,
,
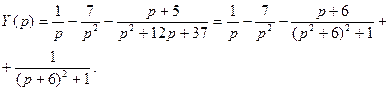
Переходя к оригиналам, получим искомое решение:
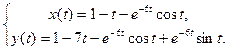
Модуль 10
Теория вероятностей
Задачи для решения
Задание 1
Непосредственный подсчет вероятностей событий
Варианты
1. В партии из 15 деталей имеется 10 стандартных. Наудачу
отобраны 5 деталей. Найти вероятность того, что среди
отобранных деталей 4 стандартных.
2. В цехе работают 6 мужчин и 4 женщины. По табельным
номерам наудачу отобраны 7 человек. Найти вероятность
того, что среди отобранных лиц окажутся 3 женщины.
3. На складе имеется 12 кинескопов, причем 10 из них
изготовлены Львовским заводом. Найти вероятность того,
что среди наудачу взятых 5 кинескопов окажутся 3
кинескопа Львовского завода.
4. В группе 20 студентов, среди которых 3 отличника. По
списку наудачу отобраны 12 студентов. Найти вероятность
того, что среди отобранных студентов окажутся 2 отличника.
5. В коробке имеется 15 одинаковых изделий, причем 3 из них
окрашены. Наудачу извлечены 2 изделия. Найти вероятность
того, что среди извлеченных изделий одно окрашено.
6. На объект производится налет девяти однотипных
самолетов, из которых 2 являются носителями специального
оружия. Силами ПВО сбито 5 самолетов. Найти вероятность
того, что сбиты оба носителя специального оружия.
7. Из урны, в которой находится 5 белых и 4 черных шара,
наудачу вынимают 2 шара. Найти вероятность того, что оба
вынутых шара разноцветные.
8. Из 10 лотерейных билетов 3 являются выигрышными. Найти
вероятность того, что среди 5 наудачу выбранных билетов
один билет является выигрышным.
9. Среди 7 винтовок 2 являются непристреленными. Найти
вероятность того, что среди 3 наудачу выбранных винтовок,
одна окажется непристреленной.
10. Среди 12 часов, 8 штук нуждаются только в общей чистке.
Найти вероятность того, что из 6 наудачу выбранных часов,
3 будут нуждаться только в общей чистке.
Задание 2
Теоремы сложения и умножения вероятностей
Варианты
1. Для сигнализации об аварии установлены 2 сигнализатора.
Вероятность того, что при аварии сработает первый
сигнализатор, равна 0,95, второй – 0,9. Найти вероятность
того, что при аварии сработает только один сигнализатор.
2. Для разрушения моста достаточно попадания одной
авиационной бомбы. Найти вероятность того, что мост будет
разрушен, если на него будут выброшены 4 бомбы с
вероятностями попадания, соответственно равными
0,3; 0,4; 0,6; 0,7.
3. Два стрелка стреляют по мишени. Вероятность попадания в
мишень при одном выстреле для первого стрелка равна 0,7, а
для второго 0,8. Найти вероятность того, что при одном залпе
в мишень попадает только один из стрелков.
4. Из партии изделий товаровед отбирает изделия высшего
сорта. Вероятность того, что наудачу взятое изделие окажется
высшего сорта, равна 0,8. Найти вероятность того, что из трех
проверенных изделий будет только 2 изделия высшего сорта.
5. Самолет противника захватывается тремя РЛС независимо
друг от друга соответственно с вероятностями 0,8; 0,6 и 0,5.
Найти вероятность захвата самолета всеми тремя станциями.
6. Для некоторой местности среднее число пасмурных дней в
июле равно шести. Найти вероятность того, что первого и
второго июля будет ясная погода.
7. Студент знает 20 из 25 вопросов программы. Найти
вероятность того, что студент знает предложенные ему
экзаменатором 3 вопроса.
8. Два охотника стреляют по оленю. Первый охотник может
попасть в оленя с вероятностью 0,7, а второй – с вероятностью 0,6. Найти вероятность того, что в оленя охотники не попадут.
9. Студент разыскивает нужную ему формулу в трех
справочниках. Вероятность того, что формула содержится в
первом, втором и третьем справочнике соответственно равны
0,6; 0,7; 0,8. Найти вероятность того, что формула содержится
только в одном справочнике.
10. В цехе работают 7 мужчин и 3 женщины. По табельным
номерам отобрали 3 человека. Найти вероятность того, что все
отобранные лица окажутся мужчинами.
Задание 3
Формула полной вероятности. Формула Байеса
Варианты
1. Имеются 2 одинаковые на вид урны. В одной из них 5 белых и 3 черных шара, а в другой 4 белых и 5 черных шаров. Из наудачу выбранной урны наудачу был извлечен черный шар. Из какой урны вероятнее всего он был извлечен?
2. Среди семи винтовок три винтовки являются непристреленными. Вероятность попадания в цель из пристреленной винтовки равна 0,8, а из непристреленной 0,1. Выстрелом из наудачу взятой винтовки цель поражена. Найти вероятность того, что поражение цели было произведено из непристреленной винтовки.
3. Стрельба подводной лодки по береговому объекту может производиться с одной из трех позиций, вероятности выхода на которые равны соответственно 0,2; 0,3 и 0,5. Вероятности поражения цели с данных позиций равны соответственно 0,85; 0,75; 0,4. Произведена стрельба, в результате которой цель была поражена. С какой позиции вероятнее всего производилась стрельба?
4. Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых автомашин как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1. Для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.
5. Три стрелка произвели залп, причем две пули поразили мишень. Найти вероятность того, что третий стрелок поразил мишень, если вероятность попадания в мишень первым, вторым и третьим стрелками соответственно равны 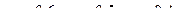 .
.
6. Два из трех независимо работающих элементов устройства отказали. Найти вероятность того, что отказали первый и второй элементы, если вероятности отказа первого, второго и третьего элементов соответственно равны 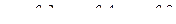 .
.
7. Два автомата производят одинаковые детали, которые сбрасываются на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60% деталей отличного качества, а второй – 84%. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь произведена первым автоматом.
8. Из 18 стрелков 6 попадают в мишень с вероятностью 0,9; 7 – с вероятностью 0,8; 3 – с вероятностью 0,6 и 2 с вероятностью 0,5. Наудачу выбранный стрелок производит два выстрела и делает промахи. К какой группе вероятнее всего принадлежал стрелок?
9. При разрыве снаряда обнаруживаются осколки трех категорий: крупные, средние и мелкие в количестве, соответственно, 10%, 30% и 60%. При попадании в броню крупный пробивает её с вероятностью 0,9; средний 0,2 и мелкий 0,05. В результате разрыва снаряда в броню попал один осколок и пробил её. Какова вероятность того, что осколок крупный?
10. Имеется три партии по 20 деталей в каждой. Число стандартных деталей в первой, второй и третьей партиях соответственно равно 20, 15, 10. Из наудачу взятой партии наудачу извлечена деталь, оказавшаяся стандартной. Найти вероятность того, что деталь была извлечена из третьей партии.
Задание 4
Повторение испытаний. Формула Бернулли
Вероятность попадания стрелком в цель равна р. Сделано п выстрелов. Найти:
a) Вероятность промаха;
b) Вероятность поражения цели;
c) Вероятность к попаданий в цель.
Варианты
| 1. | р=0,4; | п=5; | к=3. |
| 2. | р=0,6; | п=10; | к=2. |
| 3. | р=0,5; | п=7; | к=1. |
| 4. | р=0,9; | п=8; | к=3. |
| 5. | р=0,8; | п=6; | к=2. |
| 6. | р=0,5; | п=12; | к=4. |
| 7. | р=0,6; | п=4; | к=2. |
| 8. | р=0,3; | п=10; | к=3. |
| 9. | р=0,4; | п=8; | к=1. |
| 10. | р=0,3; | п=6; | к=2. |
Задание 5
Дискретные случайные величины
По цели произведено два независимых выстрела с вероятностями попадания при каждом выстреле соответственно р1 и р2. Для случайного числа попаданий в цель составить ряд и функцию распределения. Построить их графики. Найти М[х],D[x],G[x].
Варианты.
| 1. | р1=0,4; | р2=0,5. |
| 2. | р1=0,3; | р2=0,6. |
| 3. | р1=0,2; | р2=0,3. |
| 4. | р1=0,1; | р2=0,7. |
| 5. | р1=0,6; | р2=0,4. |
| 6. | р1=0,7; | р2=0,5. |
| 7. | р1=0,8; | р2=0,3. |
| 8. | р1=0,9; | р2=0,2. |
| 9. | р1=0,5; | р2=0,8. |
| 10. | р1=0,4; | р2=0,7. |
Задание 6
Непрерывные случайные величины
Непрерывная случайная величина Х задана плотностью распределения р(х). Требуется:
1). Определить коэффициент С;
2). Найти функцию распределения F(x);
3). Построить графики р(x) и F(x);
4). Найти вероятность того, что случайная величина Х принимает значение из интервала (α; β).
Варианты.
| 1. | 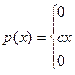 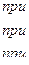 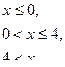
| α=2; β=3 |
| 2. | 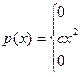 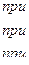 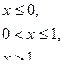
| α=-5; β=0,5 |
| 3. | 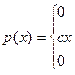 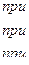 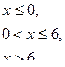
| α=1; β=3 |
| 4. | 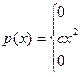 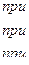 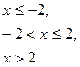
| α=0; β=1 |
| 5. | 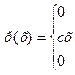 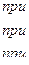 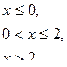
| α=0; β=3 |
| 6. | 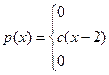 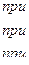 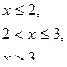
| α=1; β=2,5 |
| 7. | 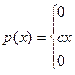 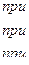 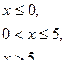
| α=2; β=3 |
| 8. | 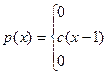 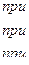 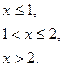
| α=1,5; β=2 |
| 9. | 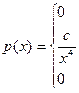 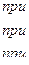 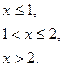
| α=1; β=3/2 |
| 10. | 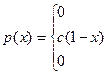 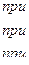 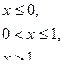
| α=0,5; β=1 |
Задание 7
Нормальный закон распределения случайной величины
Случайная величина Х подчиняется нормальному закону с параметрами m и σ.
Составить плотность распределения этой случайной величины р(х) и найти вероятность того, что случайная величина попадет в интервал (α;β).
Варианты
| 1. | m =3 | σ =2 | α = -3; β = 2 |
| 2. | m =0 | σ =4 | α = -2; β = 3 |
| 3. | m =-2 | σ =2 | α = 0; β = 4 |
| 4. | m =6 | σ =2 | α = 4; β = 8 |
| 5. | m =20 | σ =10 | α = 17; β = 23 |
| 6. | m =2 | σ =0,5 | α = 0; β = 4 |
| 7. | m =5 | σ =20 | α = 0; β = 15 |
| 8. | m =4 | σ =0,5 | α = 3; β = 5 |
| 9. | m =20 | σ =10 | α = 10; β = 30 |
| 10. | m =0 | σ =14 | α = -10; β = 10 |
Решение типовых задач
Задание 1
У рабочего 20 однотипных деталей, из которых окрашено в красный цвет 9 деталей, в зеленый цвет 7 деталей и в синий 4 детали. Рабочий наудачу берет 6 деталей. Найти вероятность того, что среди выбранных деталей окажется 3 красных, 2 зеленых и 1 синяя.
Задание 2
В читальном зале имеется 6 учебников по теории вероятностей, из которых 3 в твёрдом переплете. Библиотекарь наудачу взял 2 учебника. Найти вероятность того, что оба учебника окажутся в твёрдом переплете.
Задание 3
В пирамиде установлены 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0.95; для винтовки без оптического прицела эта вероятность равна 0.8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него?
Задание 4
По цели производится 5 независимых выстрелов. Вероятность попадания в цель при одном выстреле равна 0.6. Для получения зачета по стрельбе требуется не менее трех попаданий. Найти вероятность получения зачета.
Задание 5
Два стрелка сделали по одному выстрелу в мишень. Вероятность попадания для первого стрелка 0.3, для второго – 0.4.
Для случайного числа попаданий в цель составить ряд и функцию распределения. Построить их графики. Найти M[x], D[x], σ[x].
Задание 6
Непрерывная случайная величина задана плотностью распределения
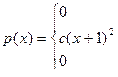
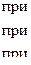
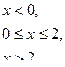
Требуется:
1) определить коэффициент с;
2) найти функцию распределения F(х);
3) построить графики f(х) и F(х);
4) найти вероятность того, что случайная величина Х принимает
значения из интервала (1; 2).
Задание 7
Случайная величина подчинена нормальному закону с параметрами т = 3 и σ = 2. Составить плотность распределения этой случайной величины f(х) и найти вероятность того, что случайная величина попадет в интервал (- 1; 4).
Сведения из теории
Классификация событий
Случайным событием называется событие, которое может произойти или не произойти в определенных условиях. Эти условия называются опытом или испытанием.
Два события называются взаимно противоположными, если наступление одного из них приводит к ненаступлению другого.
Неслучайное событие называется достоверным, если оно в результате испытания не может не наступить, и невозможным, если оно в результате испытания не может наступить.
Два события называются несовместными, если наступление одного из них исключает наступление другого, и совместными, если наступление одного из них не исключает наступления другого в одном и том же испытании.
Два события называют независимыми, если наступление одного из них никак не отражается на возможности наступления другого, и зависимыми, если наступление одного из них определенным образом отражается на возможности наступления другого.
Дата: 2018-12-28, просмотров: 484.