© Академия военно-морских сил имени П.С. Нахимова, 2013
ПРЕДИСЛОВИЕ.
Пособие содержит материалы, необходимые для подготовки к успешной сдаче экзаменов по дисциплине «высшая математика» в І, ІІ, ІІІ, IV учебных семестрах.
В каждом семестре предусмотрено выполнение учащимися заданий модульного контроля по указаным темам. Материалы пособия, относящиеся к определённому семестру, содержат:
· краткое изложение основных теоретических сведений;
· примеры выполнения типовых практических задач;
· контрольные вопросы по теоретическому материалу, вынесенные на семестровый экзамен;
· типовые практические задачи для самостоятельного выполнения (десять вариантов) по каждому модулю;
В сборнике приведён список рекомендуемой литературы по каждому модулю.
I семестр
Вопросы
1. Классификация систем линейных алгебраических уравнений и их решений.
2. Матрицы систем линейных алгебраических уравнений и их виды.
3. Определитель квадратной матрицы и его вычисление.
4. Обратная матрица и ее нахождение.
5. Решение и исследование систем линейных алгебраических уравнений по формулам Крамера.
6. Решение и исследование систем линейных алгебраических уравнений матричным способом.
7. Решение и исследование систем линейных алгебраических уравнений по способу Гаусса.
8. Скалярные и векторные величины, линейные операции над векторами.
9. Скалярное произведение векторов и его свойства. Угол между двумя векторами. Условие перпендикулярности двух векторов.
10. Векторное произведение векторов и его свойства. Условие коллинеарности двух векторов.
11. Смешанное произведение векторов и его свойства. Условие компланарности трех векторов.
12. Прямая линия на плоскости. Виды уравнения прямой.
13. Основные задачи на прямую линию на плоскости.
14. Канонические уравнения линий второго порядка. Их характерные точки и линии.
15. Плоскость. Различные виды уравнений плоскости. Уравнение плоскости, проходящей через три точки.
16. Основные задачи на плоскость.
17. Уравнение прямой в пространстве.
18. Основные задачи на прямую в пространстве.
19. Пределы функций и числовых последовательностей.
20. Теоремы о пределах суммы, произведения и частного функций.
21. Неопределенные выражения и их раскрытие.
22. Первый и второй замечательные пределы.
23. Непрерывность функций. Точки разрыва.
24. Производная и дифференциал функций.
25. Дифференцирование суммы, произведения и частного функций.
26. Дифференцирование сложной функции.
27. Дифференцирование функции, заданной неявно и параметрически.
28. Уравнения касательной прямой и нормали к графику функции.
29. Повторное дифференцирование.
30. Исследование функций и построение графиков.
31. Комплексные числа и действия над ними.
Модуль 1
Линейная алгебра. Векторная алгебра
Задачи для решения.
Задание 1
Исследовать систему по теореме Кронекера-Капелли, если система совместна и определена, то решить по формулам Крамера, матричным способом и способом Гаусса.
Варианты
1. 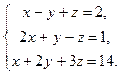 2.
2. 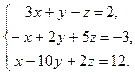
3. 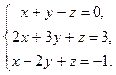 4.
4. 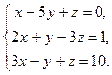
5. 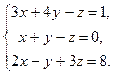 6.
6. 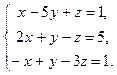
7. 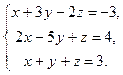 8.
8. 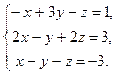
9.  10.
10. 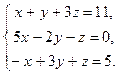
Задание 2
Даны координаты вершин пирамиды А1 А2 А3 А4:
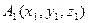 ,
, 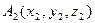 ,
, 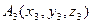 ,
,  .
.
Найти:
а) длину ребра [А1А 2];
б) угол между ребрами [А1А2] и [А1 А4];
в) проекцию вектора 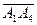 на
на 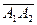 ;
;
г) площадь грани А1 А2 А3 ;
д) объем пирамиды А1 А2 А3 А4.
Варианты .
1. А1(3,1,4), А2 (-1,6,1), А3 (-1,1,6), А4(0,4,-1);
2. А1 (3,3,9), А2 (6,9,1), А3(1,7,3), А4(8,5,8);
3. А1(3,5,4), А2 (5,8,3), А3 (1,9,9), А4(6,4,8);
4. А1 (2,4,3), А2 (7,6,3), А3 (4,9,3), А4(3,6,7);
5. А1 (9,5,5), А2 (-3,7,1), А3(5,7,8), А4(6,9,12);
6. А1 (0,7,1), А2 (4,1,5), А3 (4,6,3), А4(3,9,8);
7. А1 (5,5,4), А2 (3,8,4), А3(3,5,10), А4(5,8,2);
8. А1(6,1,1), А2(4,6,6), А3(4,2,0), А4(1,2,6);
9. А1(7,5,3), А2 (9,4,4), А3 (4,5,7), А4(7,9,6);
10. А1(6,6,2), А2(5,4,7), А3(2,4,7), А4(7,3,0).
Решение типовых задач
Задание 1
Исследовать систему по теореме Кронекера-Капелли, если система совместна и определена, то решить по формулам Крамера, матричным способом и способом Гаусса.
Если система совместна, но не определена, найти общее и одно частное решение.
а) 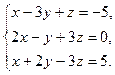 б)
б) 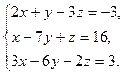
в) 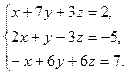
Задание 2
Даны координаты вершин пирамиды А1 А2 А3 А4.
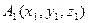 ,
, 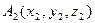 ,
, 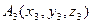 ,
,  .
.
Найти:
а) длину ребра [А1А2];
б) угол между ребрами [А1А2] и [А1 А4];
в) проекцию вектора 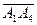 на
на 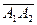 ;
;
г) площадь грани А1 А2 А3 ;
д) объем пирамиды А1 А2 А3 А4.
А1 (3;2-3), А2 (5;1;-1), А3 (-1;2; -1), А4 (1;-2;1).
Пример выполнения задания 1
а) Дана система линейных алгебраических уравнений:
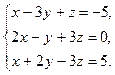
Найдём ранг матрицы А, составленной из коэффициентов при неизвестных. Путём элементарных преобразований приведём эту матрицу к ступенчатому виду.
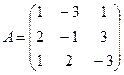 ~
~ 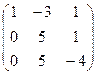 ~
~  .
.
Ранг матрицы системы r(A)=3 .
Найдём ранг расширенной матрицы 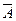 .
.
 ~
~ 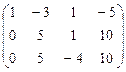 ~
~  .
.
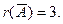
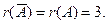
Ранг расширенной матрицы равен рангу матрицы А и числу неизвестных, следовательно, система совместна и обладает единственным решением. Найдём это решение по формулам Крамера, которые имеют вид:
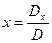 ,
, 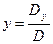 ,
, 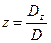 .
.
Находим основной определитель системы:
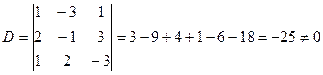 .
.
Определитель системы не равен нулю, это так же означает, что система имеет единственное решение.
Находим определители неизвестных.
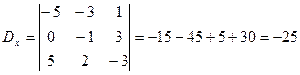 ,
,
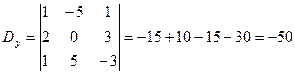 ,
,
 .
.
Подставив найденные значения определителей в формулы
Крамера, получим решение системы.
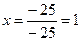 ,
, 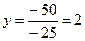 ,
, 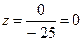 .
.
Ответ: х =1, у =2, z =0.
Решим данную систему матричным способом.
Эта система уравнений может быть записана в виде следующего матричного уравнения: AХ=B.
Матричное решение имеет вид: Х =А-1В.
Найдём матрицу А-1 обратную матрице системы:  .
.
Матрица системы имеет вид:
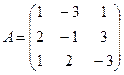 .
.
Её определитель det A уже найден: det A = D = - 25.
Составим транспонированную матрицу:
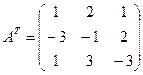 .
.
Составляем присоединенную (союзную) матрицу С, состоящую из алгебраических дополнений элементов матрицы АТ, для чего вычисляем алгебраические дополнения элементов транспонированной матрицы:
 .
.
Находим решение системы в матричной форме:
Х = 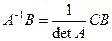 =
= 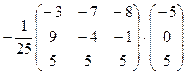 ,
,
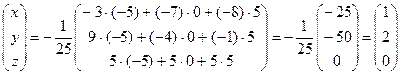 .
.
Ответ: х = 1, у = 2, z = 0.
Решим данную систему методом Гаусса.
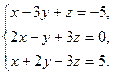
Исключим х из второго и третьего уравнения. Для этого из второго уравнения вычтем удвоенное первое, из третьего уравнения вычтем первое.
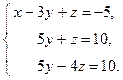
Исключим из третьего уравнения у. Для этого вычтем из него второе уравнение.
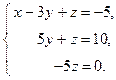
Из третьего уравнения находим z. Подставив его значение во второе уравнение, найдём у. Подставив значения х и у в первое уравнение, найдём х.
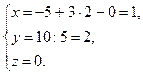
Ответ: х = 1, у = 2, z = 0.
б) Дана система линейных алгебраических уравнений:
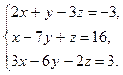
Найдём ранг матрицы А, составленной из коэффициентов при неизвестных.
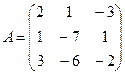 ~
~ 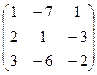 ~
~ 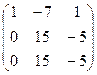 ~
~ 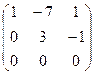
Её ранг r (A) = 2.
Найдём ранг расширенной матрицы  .
.
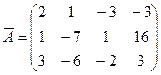 ~
~ 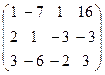 ~
~ 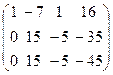 ~
~ 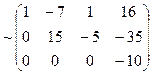 .
.
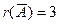 .
.
 .
.
Ответ: Система не совместна.
в) Дана система линейных алгебраических уравнений:
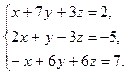
Найдём ранг матрицы А, составленной из коэффициентов при неизвестных.
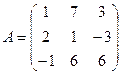 ~
~ 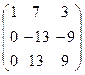 ~
~ 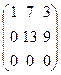 .
.
Её ранг r (A) = 2.
Найдём ранг расширенной матрицы системы.
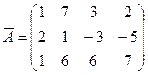 ~
~  ~
~  .
.
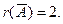

Система совместна, но не определена. Найдём решение этой системы. Восстановим систему по последней матрице.
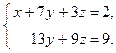
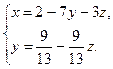
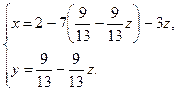 .
.
Ответ: 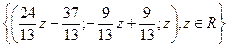 .
.
Пример выполнения задания 2
Даны координаты вершин пирамиды А1А2А3А4:
А1 (3;2;-3), А2 (5;1;-1), А3 (-1;2; -1), А4 (1;-2;1).
Найдём координаты 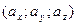 ,
,  ,
, 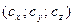
векторов 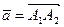 ;
; 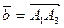 ;
;  .
.
 .
.
Получим:
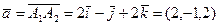 ,
,
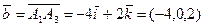 ,
,
 .
.
а) Длина ребра [А1 А2] пирамиды равна длине вектора 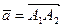 . Длина вектора определяется по формуле:
. Длина вектора определяется по формуле:
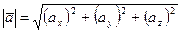 , следовательно:
, следовательно:
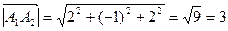 .
.
б) Угол 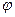 между рёбрами [А1А2] и [А1 А3] пирамиды равен углу между векторами
между рёбрами [А1А2] и [А1 А3] пирамиды равен углу между векторами  и
и 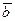 . Косинус угла между векторами определяется по формуле:
. Косинус угла между векторами определяется по формуле:
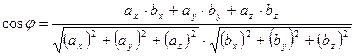 ,
,
следовательно,
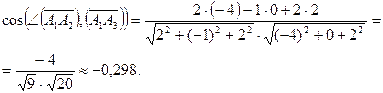
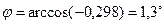 .
.
в) Проекция вектора 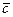 на направление вектора
на направление вектора 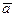 определяется
определяется
по формуле: 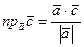 , следовательно,
, следовательно,
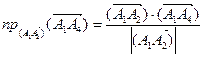 ,
,
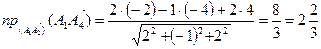 .
.
г) Определим площадь грани (А1А2А3) по формуле для вычисления площади треугольника с помощью модуля векторного произведения векторов 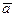 и
и 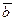 :
:
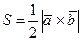 , где
, где  .
.
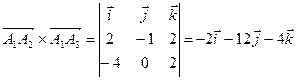
 .
.
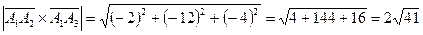 .
.
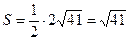 (ед2).
(ед2).
д) Объем пирамиды, построенной на векторах 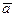 ,
, 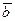 ,
, 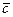 определяем с помощью смешанного произведения векторов по формуле:
определяем с помощью смешанного произведения векторов по формуле:
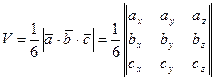 .
.
V = 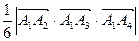 .
.
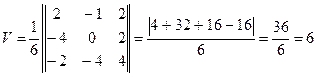 (ед3).
(ед3).
Модуль 2
Аналитическая геометрия на плоскости
и в пространстве
Задачи для решения
Задание 1
Дана кривая второго порядка. Найти ее вершины, фокусы, эксцентриситет. Для гиперболы составить уравнение асимптот. Построить кривую второго порядка.
Варианты
1. 9x2 + 16y2 = 144;
2. 4x2 – 9y2 = 36;
3. 9x2 + 25y2 = 225;
4. 16x2 – 9y2 = 144;
5. x2 +4y2 = 16;
6. 25x2 – 49y2 = 1225;
7. 16x2 +9y2 = 144;
8. 16x2 – 25y2 = 400;
9. 9x2 +4y2 = 36;
10. 25x2 – 16y2 = 400.
Задание 2
Найти вершину, ось симметрии, фокус и директрису параболы. Сделать чертеж.
Варианты
1. y = 4x2 - 8x + 7;
2. y2 – 2y +5 = 2x;
3. y = x2 +4x + 12;
4. y2 – x – 6y +17 = 0;
5. y2 + 8x – 16 = 0;
6. y2 – 10x - 2y – 19 = 0;
7. x2 +4x +6y – 20 = 0;
8. y2 – 6x + 14y + 49 = 0;
9. x2 – 6x – 4y + 29 = 0;
10. x2 + 8x + 6y + 46 = 0.
Задание 3
Даны координаты вершин пирамиды А1,А2 А3 А4.
 ,
, 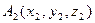 ,
,  ,
,  .
.
Найти:
а) уравнение ребра [A1A2];
б) уравнение грани А1А2А3;
в) угол между ребром [A1A4] и гранью А1А2А3;
г) уравнение высоты h, опущенной из вершины А4 на грань
А1А2А3;
д) длину d высоты h.
Варианты
1. А1(3,1,4), А2 (-1,6,1), А3 (-1,1,6), А4(0,4,-1);
2. А1 (3,3,9), А2 (6,9,1), А3(1,7,3), А4(8,5,8);
3. А1(3,5,4), А2 (5,8,3), А3 (1,9,9), А4(6,4,8);
4. А1 (2,4,3), А2 (7,6,3), А3 (4,9,3), А4(3,6,7);
5. А1 (9,5,5), А2 (-3,7,1), А3(5,7,8), А4(6,9,12);
6. А1 (0,7,1), А2 (4,1,5), А3 (4,6,3), А4(3,9,8);
7. А1 (5,5,4), А2 (3,8,4), А3(3,5,10), А4(5,8,2);
8. А1(6,1,1), А2(4,6,6), А3(4,2,0), А4(1,2,6);
9. А1(7,5,3), А2 (9,4,4), А3 (4,5,7), А4(7,9,6);
10. А1(6,6,2), А2(5,4,7), А3(2,4,7), А4(7,3,0).
Решение типовых задач
Задание 1
Дана кривая второго порядка. Найти ее вершины, фокусы, эксцентриситет. Для гиперболы составить уравнение асимптот. Построить кривую второго порядка.
а) 3x2 + 4y2 = 12; б) 9x2 – 16y2 = 144.
Задание 2
Найти вершину, ось симметрии, фокус и директрису параболы. Сделать чертеж.
Уравнение параболы y2 – 2x + 4y + 2 = 0.
Задание 3
Даны координаты вершин пирамиды А1 А2 А3 А4.
 ,
,  ,
, 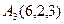 ,
, 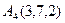 .
.
Найти:
а) уравнение ребра [A1A2];
б) уравнение грани А1А2А3;
в) угол между ребром [A1A4] и гранью А1А2А3;
г) уравнение высоты, опущенной из вершины А4 на грань А1А2А3;
д) длину высоты.
Пример выполнения задания 1
a) Дана кривая второго порядка:
3x2 + 4y2 = 12.
Это уравнение эллипса. Преобразуем его к каноническому виду 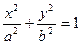 .
.
Разделим обе части уравнения на 12: 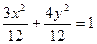 . Каноническое уравнение имеет вид:
. Каноническое уравнение имеет вид:  .
.
Большая полуось эллипса а = 2, а малая полуось 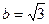 .
.
Следовательно, координаты его вершин:
А1(-2; 0), А2(2; 0), В1(0; 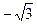 ), В2(0;
), В2(0; 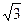 ).
).
Координаты фокусов: F1(-с; 0) ; F2(с; 0).
Найдем с по формуле:  ;
; 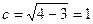 .
.
Координаты фокусов: F1(-1; 0) ; F2(1; 0).
Эксцентриситет эллипса: 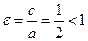 .
.
б) Дана кривая второго порядка:
9x2 – 16y2 = 144.
Это уравнение гиперболы. Преобразуем его к каноническому виду 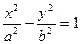 .
.
Разделим обе части уравнения на 144: 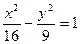 .
.
Полуоси данной гиперболы: действительная а = 4, мнимая b=3. Следовательно, ее вершины:
А1(-4;0), А2(4;0), В1(0;-3), В2(0;3).
Прямоугольник с центром в начале координат, сторонами, параллельными координатным осям и проходящими через вершины гиперболы, называется основным прямоугольником гиперболы. Его диагонали 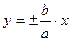 являются асимптотами гиперболы.
являются асимптотами гиперболы.
Асимптоты: 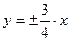 .
.
Координаты фокусов: F1(-с; 0) ; F2(с; 0).
Найдем с по формуле:  ;
; 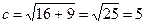 , следовательно, F1(-5;0); F2(5;0).
, следовательно, F1(-5;0); F2(5;0).
Эксцентриситет гиперболы 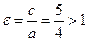 .
.
Пример выполнения задания 2
Найдём вершину, ось симметрии, фокус и директрису параболы
y2 – 2x + 4y + 2 = 0.
Приведем уравнение параболы к каноническому виду
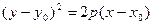 . Здесь
. Здесь 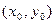 – координаты вершины,
– координаты вершины,
р – параметр параболы (расстояние между фокусом и директрисой).
Выделим в уравнении параболы полный квадрат по у:
y2 +4y + 4 – 2x – 4 + 2 = 0,
(y + 2)2 = 2x + 2.
Каноническое уравнение:
(y + 2)2 = 2(x + 1).
Координаты вершины О1(-1;-2). Парабола симметрична относительно прямой у = -2. Величина параметра р = 1.
Если вершина параболы находится в точке (0,0), то координаты её фокуса: F(p/2;0), уравнение директрисы: х = -р/2. Следовательно, наша парабола имеет фокус в точке 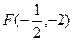 .
.
Уравнение директрисы 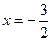 .
.
Пример выполнения задания 3
Даны координаты вершин пирамиды А1А2А3А4:
А1(0,0,1), А2 (2,3,5), А3 (6,2,3), А4(3,7,2).
а) Канонические уравнения прямой, проходящей через точки А1(х1, у1, z1) и А2(х2, у2, z2) имеют вид:
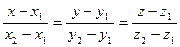 .
.
Следовательно, уравнение ребра [ 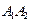 ], как уравнение прямой
], как уравнение прямой 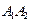 имеет вид:
имеет вид:
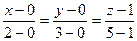 , или
, или 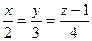 .
.
б) Составим уравнение плоскости А1А2А3 как уравнение плоскости, проходящей через три данные точки 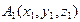 ,
,  ,
,  :
:
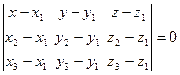 .
.
Получим:
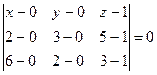 , т.е.
, т.е. 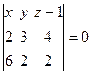 .
.
Приведём это уравнение к общему виду:
 ,
,
x(6 - 8) – y(4 – 24) + (z – 1)(4 – 18) = 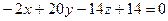 . Разделим последнее равенство на –2 и получим общее уравнение плоскости А1А2А3: x – 10y + 7z – 7 = 0.
. Разделим последнее равенство на –2 и получим общее уравнение плоскости А1А2А3: x – 10y + 7z – 7 = 0.
б) Угол между ребром [A1A4] и гранью А1А2А3 определим как угол 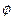 между прямой
между прямой 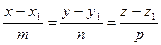 и плоскостью
и плоскостью 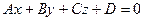 . Синус этого угла находим по формуле:
. Синус этого угла находим по формуле:
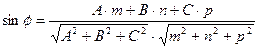 .
.
Уравнение ребра [A1A4] находим аналогично уравнению [ 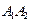 ]:
]:  .
.
Уравнение плоскости А1А2А3: x – 10y + 7z – 7 = 0.

 .
.
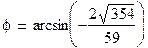 .
.
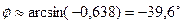 .
.
г) Составим уравнение высоты, опущенной из вершины А4 на грань А1А2А3, как уравнения прямой, проходящей через точку А4:
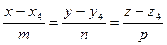 , перпендикулярно плоскости А1А2А3
, перпендикулярно плоскости А1А2А3 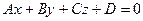 .
.
Для нахождения m, n, p используем условие перпендикулярности прямой и плоскости  .
.
Уравнение прямой:  .
.
Уравнение плоскости: x – 10y + 7z – 7 = 0.
Так как А = 1, В = -10, С = 7, то m = 1, n = -10, p = 7.
Следовательно, уравнение высоты имеет вид:
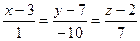 .
.
 д) Длину высоты определим по формуле для вычисления расстояния d от точки
д) Длину высоты определим по формуле для вычисления расстояния d от точки 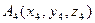 до плоскости А1А2А3
до плоскости А1А2А3 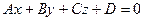 .
.
 .
.
Координаты точки А4(3,7,2).
Уравнение плоскости А1А2А3: x – 10y + 7z – 7 = 0.
Следовательно,
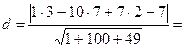
= 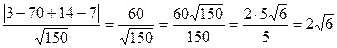 .
.
Модуль 3
Введение в математический анализ. Дифференциальное исчисление функций одной переменной
Задачи для решения
Задание 1
С помощью подходящих алгебраических преобразований или использования известных (замечательных) пределов найти пределы функций.
Варианты
1. а) 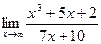 ; 2. а)
; 2. а) 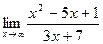 ;
;
б) 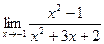 ; б)
; б) 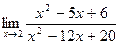 ;
;
в) 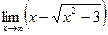 ; в)
; в) 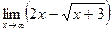 ;
;
г) 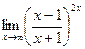 ; г)
; г) 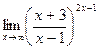 ;
;
д) 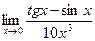 . д)
. д) 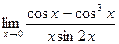 .
.
3. а)  ; 4. а)
; 4. а) 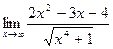 ;
;
б) 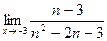 ; б)
; б) 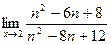 ;
;
в) 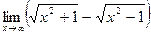 ; в)
; в) 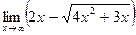 ;
;
г)  ; г)
; г) 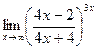 ;
;
д) 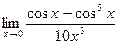 . д)
. д)  .
.
5. а) 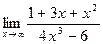 ; 6. а)
; 6. а) 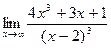 ;
;
б) 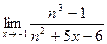 ; б)
; б) 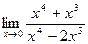 ;
;
в) 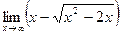 ; в)
; в) 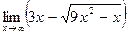 ;
;
г)  ; г)
; г) 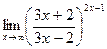 ;
;
д) 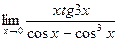 . д)
. д) 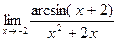 .
.
7. а) 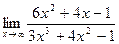 ; 8. а)
; 8. а) 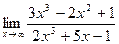 ;
;
б) 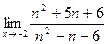 ; б)
; б)  ;
;
в)  ; в)
; в) 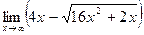 ;
;
г) 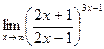 ; г)
; г) 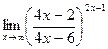 ;
;
д) 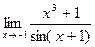 . д)
. д) 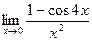 .
.
9. а) 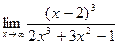 ; 10. а)
; 10. а) 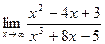 ;
;
б) 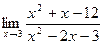 ; б)
; б) 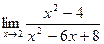 ;
;
в) 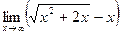 ; в)
; в)  ;
;
г) 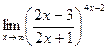 ; г)
; г)  ;
;
д) 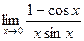 . д)
. д) 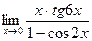 .
.
Задание 2
Найти производные первого порядка указанных функций:
Варианты
1. а) 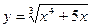 ; б)
; б) 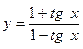 ; в) y = x · arcsin23x;
; в) y = x · arcsin23x;
г)  ; д) xsin y – y ·cos x = 0; е)
; д) xsin y – y ·cos x = 0; е) 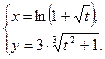
2. a) 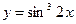 ; б)
; б) 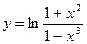 ; в)
; в)  ;
;
г)  ; д) у sin х – cos( x - у) = 0; е)
; д) у sin х – cos( x - у) = 0; е) 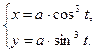
3 . a) 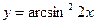 ; б)
; б) 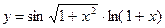 ;
;
в)  ; г)
; г) 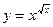 ;
;
д) 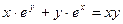 ; е)
; е) 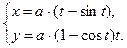
4. a) 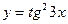 ; б)
; б)  ; в)
; в) 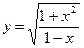 ;
;
г) 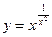 ; д)
; д)  ; е)
; е) 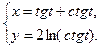
5. a) 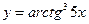 ; б)
; б) 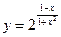 ; в)
; в) 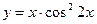 ;
;
г) 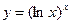 ; д)
; д) 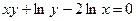 ;
;
е) 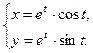
6. а) 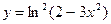 ; б)
; б) 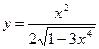 ; в)
; в) 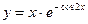 ;
;
г) 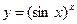 ; д)
; д)  ; е)
; е) 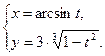 .
.
7. а)  ; б)
; б) 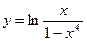 ;
;
в) 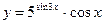 ; г)
; г) 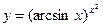 ;
;
д) 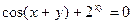 ; е)
; е) 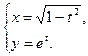
8. а) 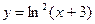 ; б)
; б) 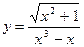 ;
;
в) 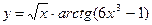 ; г)
; г) 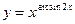 ;
;
д)  ; е)
; е) 
9. а) 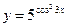 ; б)
; б)  ; в)
; в) 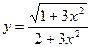 ;
;
г) 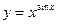 ; д)
; д) 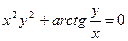 ; е)
; е) 
10. а) 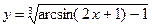 ; б)
; б) 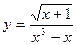 ;
;
в) 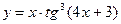 ; г)
; г)  ;
;
д) 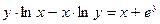 ; е)
; е) 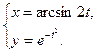
Задание 3
Найти дифференциал второго порядка указанных функций.
Варианты
1. y = arctg2х ; 2. 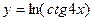 ;
;
3.  ; 4.
; 4. 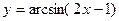 ;
;
5. 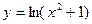 ; 6.
; 6.  ;
;
7. 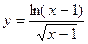 ; 8.
; 8. 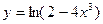 ;
;
9. y = 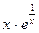 ; 10.
; 10. 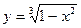
Задание 4
Произвести общее исследование функции, выявить присущие ей характерные точки, линии и области и по ним построить ее график.
Варианты
1. 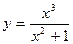 ; 2.
; 2.  ;
;
3. 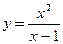 ; 4.
; 4. 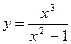 ;
;
5. 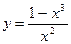 ; 6.
; 6. 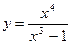 ;
;
7. 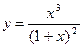 ; 8.
; 8. 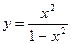 ;
;
9. 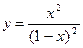 ; 10.
; 10. 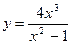 .
.
Задание 5
Найти значение выражения.
Варианты.
1. 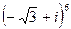 ; 2.
; 2.  ;
;
3. 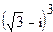 ; 4.
; 4. 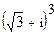 ;
;
5. 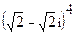 ; 6.
; 6. 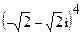 ;
;
7. 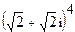 ; 8.
; 8. 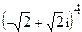 ;
;
9. 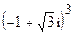 ; 10.
; 10. 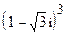 .
.
Решение типовых задач
Задание 1
С помощью подходящих алгебраических преобразований или использования известных (замечательных) пределов функций найти пределы функций.
а) 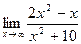 ; б)
; б) 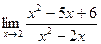 ;
;
в) 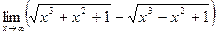 ;
;
г) 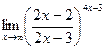 ; д)
; д) 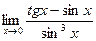 .
.
Задание 2
Найти производные первого порядка указанных функций.
а) 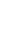 у = arcsin2(ex); б)
у = arcsin2(ex); б) 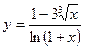 ; в)
; в) 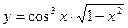 ; г)
; г) 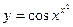 ; д) x3y2 + 5xy + 4 = 0; е)
; д) x3y2 + 5xy + 4 = 0; е) 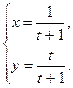

Задание 3
Найти дифференциал второго порядка функции у = ln(cos(5x)).
Задание 4
Произвести общее исследование функции 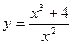 , выявить присущие ей характерные точки, линии и области и по ним построить ее график.
, выявить присущие ей характерные точки, линии и области и по ним построить ее график.
Задание 5
Выполнить над комплексными числами указанные действия:
а)  ; б)
; б) 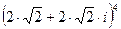 .
.
Сведения из теории
Определение предела функции
Число А называется пределом функции y = f(x) при x стремящемуся к а, если для любого сколь угодно малого положительного числа эпсилон (ε >0) найдется такое число δ (дельта), величина которого зависит от ε (δ(ε) > 0), что при всех x ≠ a и удовлетворяющих неравенству 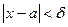 выполняется неравенство |f(x)-A| < ε. В этом случае пишут :
выполняется неравенство |f(x)-A| < ε. В этом случае пишут : 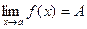 .
.
Если x →a и при этом x<a, то пишут х →a – 0.
Если x →a и при этом x >a, то пишут x → a+0.
Предел  называется левосторонним.
называется левосторонним.
Предел 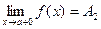 называется правосторонним.
называется правосторонним.
Число А называется пределом функции y = f(x) при х стремящемся к ∞, если для любого малого положительного числа ε (ε > 0) существует такое положительное число М, величина которого зависит от ε (М(ε) > 0), что для всех значений х, удовлетворяющих неравенству |x| > М(ε), будет выполняться неравенство |f(x)-A| < ε. В этом случае пишут 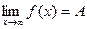 .
.
При вычислении пределов функций необходимо знать следующие теоремы:
1. 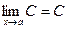 , где С – постоянная.
, где С – постоянная.
2. 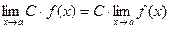 , где С – постоянная.
, где С – постоянная.
3. Если 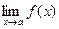 и
и  существуют, то
существуют, то
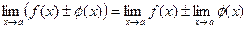 .
.
4.  .
.
5. 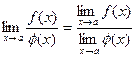 , если
, если  ≠ 0.
≠ 0.
Они справедливы как для пределов числовых последовательностей, так и для пределов функций. Перечисленные свойства справедливы как для x→a, так и для x→ ∞.
Два замечательных предела.
Первым замечательным пределом называют предел 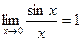 .
.
Его используют для раскрытия неопределённостей вида 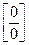 .
.
Вторым замечательным пределом называют предел

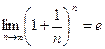 или
или 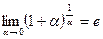 .
.
Его используют для раскрытия неопределённостей вида  .
.
Пример выполнения задания 1
а) 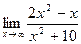 .
.
В данном случае имеем неопределенность [ 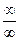 ]. Для раскрытия неопределенности разделим числитель и знаменатель на наибольшую степень переменной, то есть, разделим на x2.
]. Для раскрытия неопределенности разделим числитель и знаменатель на наибольшую степень переменной, то есть, разделим на x2.
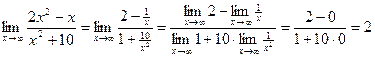 .
.
б) 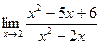 .
.
При x→2 числитель и знаменатель дроби равны нулю. Неопределенность вида [ 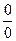 ]. Следовательно, необходимо данное выражение преобразовать.
]. Следовательно, необходимо данное выражение преобразовать.
Числитель и знаменатель данной дроби при x = 2 обращается в ноль, поэтому многочлены x2- 5x + 6 и x2 - 2x делятся без остатка на бином (x – 2) (теорема Безу).
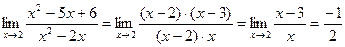
в) 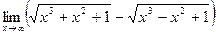 .
.
В данном случае имеем неопределенность вида [∞-∞].
Умножаем выражение, стоящее под знаком предела, на такой множитель, чтобы получить разность квадратов: 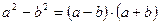 . Чтобы не нарушать тождество, на сопряжённый множитель так же и разделим.
. Чтобы не нарушать тождество, на сопряжённый множитель так же и разделим.
В результате получим:

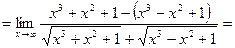
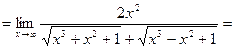
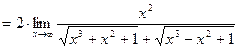
 .
.

 При x→ + ∞ числитель и знаменатель дроби – бесконечно большие величины, имеем неопределенность вида [
При x→ + ∞ числитель и знаменатель дроби – бесконечно большие величины, имеем неопределенность вида [ 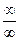 ].
].
Для раскрытия неопределенности разделим числитель и знаменатель на x2:
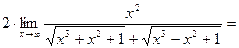
= 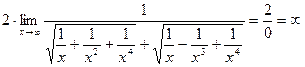 .
.
г) 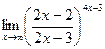 .
.
Предел основания равен 1, а показатель степени стремится к бесконечности. Имеем неопределенность вида [1∞].
Для вычисления предела преобразуем выражение так, чтобы выделить второй замечательный предел.
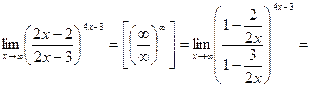
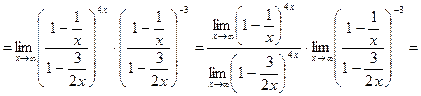
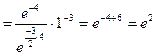 .
.
д) 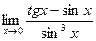 .
.
В данном случае имеем неопределенность вида [ 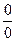 ].
].
Для вычисления предела преобразуем выражение так, чтобы выделить первый замечательный предел.

 =
=
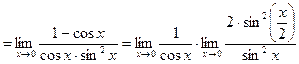 .
.
Домножаем числитель и знаменатель дроби на х2:
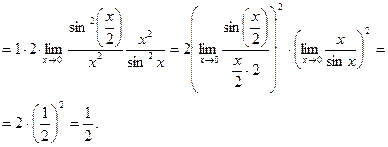
Сведения из теории
Непрерывность функции
Функция y = f(x) называется непрерывной в точке х = а, если
1) функция определена в этой точке и ее окрестности;
2) существует 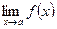 ;
;
3) предел фнкии равен значению функции в точке а, т.е. 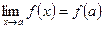 .
.

 Если хотя бы одно из этих условий не выполняется, то функция называется разрывной в точке а, а сама точка а называется точкой разрыва.
Если хотя бы одно из этих условий не выполняется, то функция называется разрывной в точке а, а сама точка а называется точкой разрыва.
Если 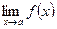 не существует, но существует оба односторонних предела в точке а, которые не равны друг другу, то разрыв в точке а называется разрывом первого рода или скачком.
не существует, но существует оба односторонних предела в точке а, которые не равны друг другу, то разрыв в точке а называется разрывом первого рода или скачком.
Если хотя бы один из односторонних пределов не существуют или равен бесконечности, а, следовательно, не существует и 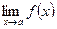 , то разрыв в точке а называется разрывом второго рода.
, то разрыв в точке а называется разрывом второго рода.
Если 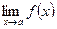 существует, но функция f(x) в точке а не определена или определена, но так, что
существует, но функция f(x) в точке а не определена или определена, но так, что  , то разрыв в точке а называется устранимым.
, то разрыв в точке а называется устранимым.
Рассмотрим функцию:
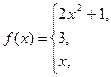
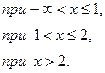
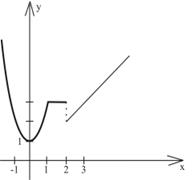 Область определения ее – вся числовая ось. Разрывы возможны лишь в точках x = 1, x = 2, в которых функция изменяет аналитическое выражение. Найдем односторонние пределы в точках х = 1, х = 2.
Область определения ее – вся числовая ось. Разрывы возможны лишь в точках x = 1, x = 2, в которых функция изменяет аналитическое выражение. Найдем односторонние пределы в точках х = 1, х = 2.
При х = 1
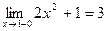 ;
; 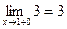 так как f(1-0) = f(1+0) = 3, то в точке х = 1 функция непрерывна.
так как f(1-0) = f(1+0) = 3, то в точке х = 1 функция непрерывна.
При х = 2
 ;
; 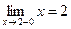 ,
,
так как f(2-0) ≠ f(2+0), то в точке
х = 2 функция имеет разрыв первого рода. Скачок функции в этой точке равен 1.
Асимптоты графика функции
Под асимптотой графика функции понимают такую прямую линию, к которой неограниченно приближаются точки графика функции у = f(x) по мере их удаления в ± ∞.
Если  , то х = а – уравнение вертикальной асимптоты.
, то х = а – уравнение вертикальной асимптоты.
Если 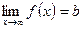 , то у = b – уравнение горизонтальной асимптоты.
, то у = b – уравнение горизонтальной асимптоты.
Если 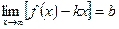 , то у = kx + b – уравнение наклонной асимптоты.
, то у = kx + b – уравнение наклонной асимптоты.
Производная и дифференциал
Производной функции у = f(х) по аргументу х называется предел отношения приращения функции к приращению независимого переменного при условии, что последнее стремится к нулю.
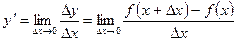 .
.
Дифференциалом dy функции у = f'(х) называется произведение производной этой функции на приращение независимого переменного Δх, т.е. dy = f'(х)Δх.
Дифференциал независимого переменного dx, по определению, равен приращению независимого переменного Δх, поэтому dy = f'(x)dx , т.е. дифференциал функции равен произведению производной функции на дифференциал независимого переменного.
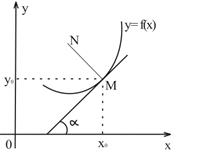 Геометрический смысл производной
Геометрический смысл производной
Пусть у = f(х) – уравнение некоторой кривой, а М(x0;у0) – точка, лежащая на этой кривой, так что у0 = f(х0).
Производная f'(x0) численно равна тангенсу угла наклона касательной к графику функции, проведенной через точку М(x0;у0), т.е.
f '(x0) = tg α, где α – угол между касательной к данной кривой, проведенной через точку М, и положительным направлением оси абсцисс.
Уравнение касательной к данной кривой у = f(x), проходящей через точку М(x0;у0) кривой, имеет вид y - y0 = f’(x0) ∙ (x – x0).
Нормалью (MN) к кривой в данной точке М(x0;у0) называется перпендикуляр к касательной, проведенный через точку касания. Уравнение нормали (MN) записывается так:
 .
.
Операция отыскания производной f '(x) данной функции f(x) называется дифференцированием этой функции. Пользуясь определением, можно получить таблицу формул дифференцирования элементарных функций:
 , n ≠ 0;
, n ≠ 0; 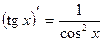 ;
;
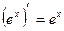 ;
; 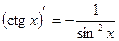 ;
;
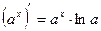 ;
; 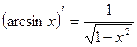 ;
;
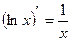 ;
; 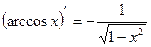 ;
;
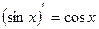 ;
; 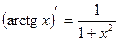 ;
;
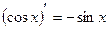 ;
; 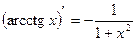 .
.
Правила дифференцирования функций
1. Производная постоянной величины равна нулю.
(С)' = 0.
2. Производная аргумента x равна 1.
x' = 1.
3. Производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
 .
.
4. Производная произведения двух функций
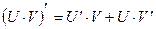 .
.
5. Постоянный множитель выносится за знак производной.
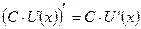 .
.
6. Производная частного двух функций
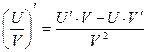 .
.
7. Производная сложной функции. Пусть у есть функция от u:
у = f(u), где u – в свою очередь функция от аргумента x: u = φ(x).
В таком случае говорят, что у есть функция от функции. Записывают у = f(φ (x)). Если для соответствующих друг другу значений x и u существуют производные f '(u) и u' = φ '(x), то существует и производная от у по x, причем имеет место равенство у' = f '(u) · u'.
Второй производной называют производную от производной и обозначают у'' : у'' = (у')' . Дифференциал второго порядка обозначают : d2y = f ''(x) dx2
Пример выполнения задания 2
Найдём производные первого порядка указанных функций.
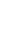 а) у = arcsin2(ex).
а) у = arcsin2(ex).
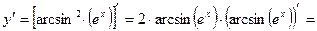
= 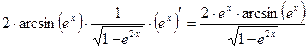 .
.
б) 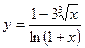 .
.
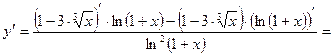
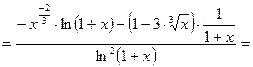
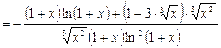 .
.
 в)
в) 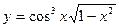 .
.

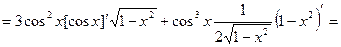
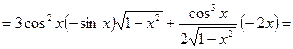
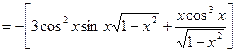 .
.
г)  .
.
Прологарифмируем левую и правую части равенства по основанию е:
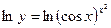 ,
,
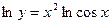 .
.
Дифференцируем, учитывая, что ln y – сложная функция, т.к.
у = у(х):
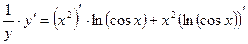 ,
,
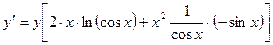 ,
,
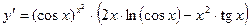 .
.
д) x3y2 + 5xy + 4 = 0.
Дифференцируем заданное соотношение, рассматривая у как функцию х:
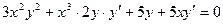 .
.
Решаем полученное уравнение относительно у':
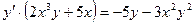 ,
,
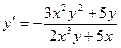
 .
.
е) 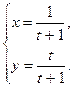

Функция задана параметрически. Производная у'х от функции по переменной х вычисляется по формуле:
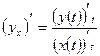 .
.
Используя данную формулу, найдем производную. Продифференцируем по t переменные х и у.
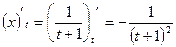 ;
;
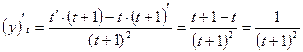 ;
;
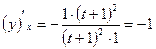 .
.
Пример выполнения задания 3
Найти дифференциал второго порядка функции у = ln(cos(5x)).
Дифференциал второго порядка определяется по формуле:
d2y = y''dx2.
 Найдем у' и
Найдем у' и 
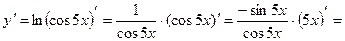
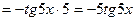 .
.
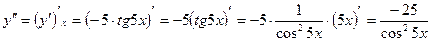 .
.
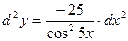 .
.
Сведения из теории
Схема исследования функций
1. Найти область определения функции.
2. Выяснить четность, нечетность, периодичность.
3. Исследовать функцию на непрерывность, найти точки
разрыва и выяснить характер разрывов.
4. Найти асимптоты графика функции.
5. Найти нули функции (у = 0) и интервалы знакопостоянства
(у > 0, y < 0).
6. Найти критические точки (у' = 0) и интервалы монотонности
(у' > 0, y' < 0).
7. Найти экстремумы функции.
8. Найти критические точки, в которых у'' = 0, и интервалы выпуклости и вогнутости.
9. Найти точки перегиба.
10. Выполнить схематический чертёж.
Пример выполнения задания 4
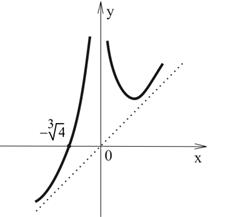
Исследуем функцию: 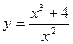 и построим её график.
и построим её график.
Решение.
Найдем первую и вторую производные этой функции.
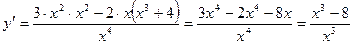 .
.
 .
.
1. Область определения:
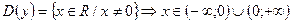 .
.
2. Функция общего вида, непериодическая.
3. Точка разрыва функции х = 0.
 , в точке х = 0 разрыв второго рода.
, в точке х = 0 разрыв второго рода.
4.  , х = 0 – вертикальная асимптота.
, х = 0 – вертикальная асимптота.
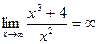 – горизонтальной асимптоты нет.
– горизонтальной асимптоты нет.
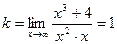 , k = 1,
, k = 1,
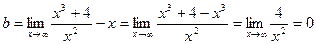 , b = 0,
, b = 0,
у = х – наклонная асимптота.
5. у = 0.
 ,
, 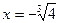 .
.
y > 0 , при 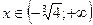 ; y < 0 , при
; y < 0 , при 
6. 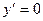 .
.
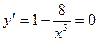 ,
,  , x = 2,
, x = 2,
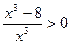
 |
7. ymin(2) = 3.
при x  (-∞; 0) функция возрастает;
(-∞; 0) функция возрастает;
при x  (0; 2) функция убывает;
(0; 2) функция убывает;
при x  (2; +∞) функция возрастает.
(2; +∞) функция возрастает.
8. у'' = 0; 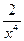 ≠ 0 – точек перегиба нет. При х = 0 вторая
≠ 0 – точек перегиба нет. При х = 0 вторая
производная не существует.
 9.
9.
График функции при 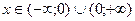 является
является
вогнутым.
10. График функции имеет вид, указанный на рисунке.
Пример выполнения задания 5
Выполним над комплексными числами указанные действия:
а) 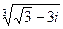 ;
;
Воспользуемся формулой:
 ,
,
где k = 0,1,…, n-1.
Запишем комплексное число, заданное в алгебраической форме, в тригонометрической форме:  , где
, где
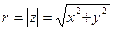 ,
, 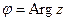 ,
,
 ,
, 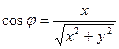 .
.
Для данного числа 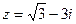
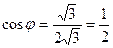 ;
;  ;
; 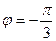 .
.
Следовательно,
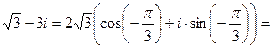
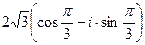 .
.
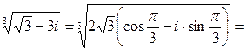
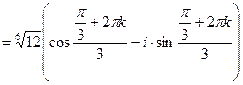 , k = 0, 1, 2.
, k = 0, 1, 2.
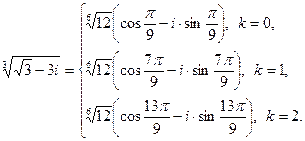
б) 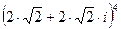 .
.
Воспользуемся формулой:
 .
.
Запишем данное комплексное число в тригонометрической форме.
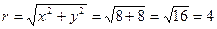 ,
,
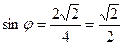 ;
; 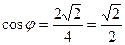 ;
;  .
.
Следовательно,
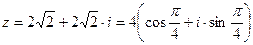 .
.
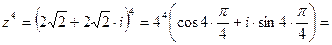
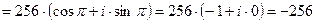 .
.
I I семестр
Вопросы
- Определение функции многих переменных, области, линии и поверхности уровня.
- Частные приращения и частные производные.
- Полное приращение и полный дифференциал.
- Производная сложной функции.
- Повторное дифференцирование.
- Дифференциал второго порядка.
- Экстремум функции двух переменных.
- Неопределенный интеграл и его свойства.
- Непосредственное интегрирование.
- Интегрирование по частям.
- Интегрирование путём внесения функции под знак дифференциала.
- Интегрирование рациональных функций.
- Интегрирование тригонометрических функций.
- Интегрирование иррациональных функций.
- Определенный интеграл и его геометрический смысл.
- Формула Ньютона-Лейбница.
- Методы интегрирования в определенном интеграле (подстановка, интегрирование по частям).
- Несобственные интегралы.
- Вычисление площадей плоских фигур в полярных и прямоугольных координатах.
- Вычисление длины дуги плоской кривой, вычисление объема тела вращения, площади поверхности вращения.
- Двойной интеграл в декартовых и полярных координатах.
- Вычисление двойного интеграла.
- Применение двойного интеграла.
- Тройной интеграл в декартовых, цилиндрических и сферических координатах.
- Применение тройного интеграла.
Модуль 4
Дифференциальное исчисление функций нескольких переменных
Задачи для решения
Задание 1
Найти частные производные функции z(х; у), заданной уравнением.
Варианты
1. 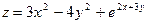 ; 2.
; 2. 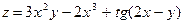 ;
;
3. 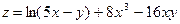 ; 4.
; 4. 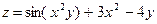 ;
;
5. 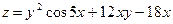 ; 6.
; 6.  ;
;
7. 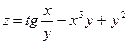 ; 8.
; 8. 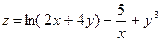 ;
;
9. 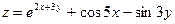 ; 10.
; 10. 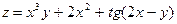 .
.
Задание 2
Найти дифференциал второго порядка заданной функции.
Варианты
1. z = sin(2x + y) + 4; 2. z = cos(3x + 2y) – 5;
3. z = xy2 – x2y; 4. z = cos(x – 2y) + 16;
5. z = sin(x– 3y) – 3; 6. z = x3y2 + x2y3;
7. z = 2x3y2 – 3x2y3; 8. z = sin(3x + 4y) – 13;
9. z = 3x2y – 2y2x; 10. z = cos(5x – y) + 6.
Задание 3
Найти производные сложных функций.
Варианты
1. a) 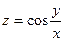 , если
, если 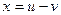 ,
, 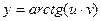 .
.
б)  , если
, если 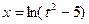 ,
, 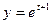 .
.
2. а) 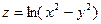 , если
, если 
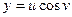 .
.
б)  , если
, если 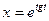 ,
, 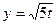 .
.
3. a)  , если
, если 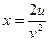 ,
, 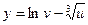 .
.
б) 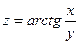 , если
, если 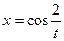 ,
, 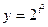 .
.
4. a) 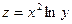 , если
, если 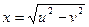 ,
, 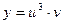 .
.
б) 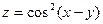 , если
, если 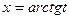 ,
, 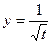 .
.
5. a) 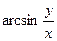 , если
, если 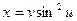 ,
, 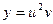 .
.
б)  , если
, если 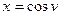 ,
, 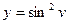 .
.
6. a) 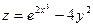 , если
, если 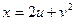 ,
, 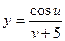 .
.
б)  , если
, если 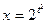 ,
, 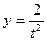 .
.
7. a) 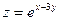 , если
, если 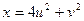 ,
, 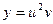 .
.
б)  , если
, если  ,
, 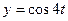 .
.
8. a) 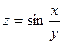 , если
, если 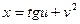 ,
, 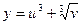 .
.
б) 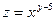 , если
, если 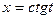 ,
, 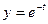 .
.
9. a) 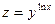 , если
, если 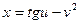 ,
, 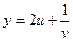 .
.
б) 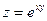 , если
, если 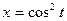 ,
, 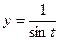 .
.
10. a)  , если
, если 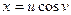 ,
, 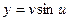 .
.
б) 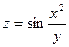 , если
, если 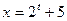 ,
, 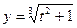 .
.
Решение типовых задач
Задание 1
Найти частные производные функции z(х; у), заданной уравнением
z = х2y + у2х + cos(2x – 3y).
Задание 2
Найти дифференциал второго порядка для функции
z = sin (3x - y) + e2x + y.
Задание 3
Выполнить дифференцирование сложных функций:
а) Найти производные 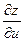 и
и 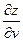 функции
функции 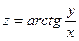 , если
, если 
б) Найти производную 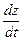 функции
функции 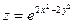 , если
, если 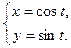
Пример выполнения задания 1
Найдём частные производные функции, заданной уравнением
z = х2y + у2х + cos(2x – 3y).
Решение.
Дифференцируем функцию двух переменных z = z(x; y) по х.
Другая переменная у при этом считается постоянной величиной.
 .
.
Дифференцируем функцию z по у, переменная х при этом считается постоянной величиной.
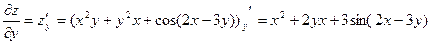 .
.
Ответ: 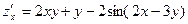 ,
,
 .
.
Пример выполнения задания 2
Найдём дифференциал второго порядка для функции
z = sin (3x - y) + e2x + y.
Решение.
Определяем первые и вторые частные производные  ,
, 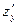 ,
, 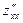 ,
, 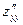 ,
, 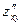 и подставляем их в формулу дифференциала второго порядка:
и подставляем их в формулу дифференциала второго порядка:
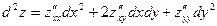
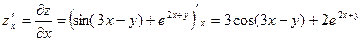 ;
;
 ;
;
 ;
;
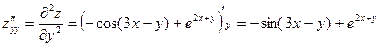 ;
;
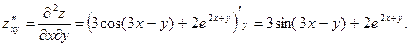
Дифференциал второго порядка равен:
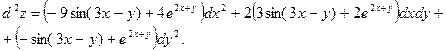
Ответ:
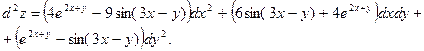
Пример выполнения задания 3
Выполним дифференцирование сложных функций.
а) Найдём производные 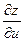 и
и 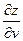 функции
функции 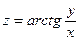 ,
,
если 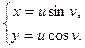
Решение.
Частные производные 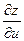 и
и 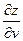 сложной функции
сложной функции 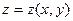 ,
,
если 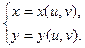 , находят по формулам:
, находят по формулам:
 ,
,  .
.
Найдём частные производные 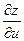 и
и 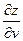 сложной функции
сложной функции  ,
, 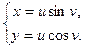
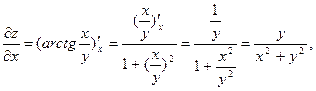
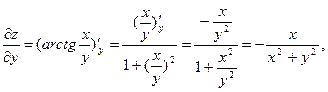
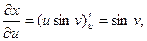


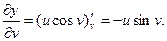
Подставим в формулы для нахождения 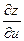 и
и 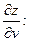
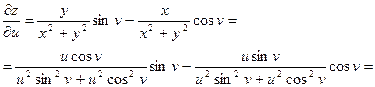
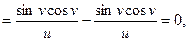
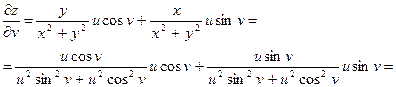
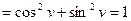 .
.
Ответ :  ;
; 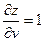 .
.
б) Найдём производную 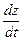 функции
функции 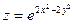 , если
, если
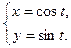
Решение.
Пусть функция 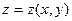 - дифференцируемая функция аргументов x и y, а x и y являются дифференцируемыми функциями аргумента t. Сложная функция
- дифференцируемая функция аргументов x и y, а x и y являются дифференцируемыми функциями аргумента t. Сложная функция 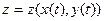 также дифференцируема, и ее производная находится по формуле:
также дифференцируема, и ее производная находится по формуле:
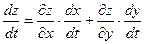 .
.
Найдём производную 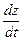 функции
функции 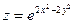 .
.
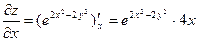 ,
, 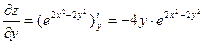 ,
,
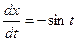 ,
,  .
.
Полученные производные подставим в формулу для нахождения 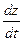 .
.
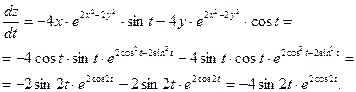
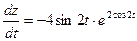 .
.
Модуль 5
Интегральное исчисление функции одной переменной
Задачи для решения
Задание 1
Непосредственным интегрированием найти следующие интегралы:
Вариант № 1 Вариант № 2
1. 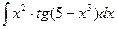 ; 1.
; 1.  ;
;
2. 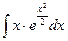 ; 2.
; 2.  ;
;
3. 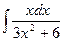 ; 3.
; 3. 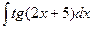 ;
;
4. 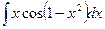 . 4.
. 4. 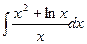 .
.
Вариант № 3 Вариант № 4
1. 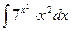 ; 1.
; 1. 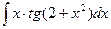 ;
;
2. 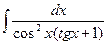 ; 2.
; 2. 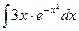 ;
;
3. 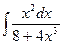 ; 3.
; 3.  ;
;
4.  . 4.
. 4.  .
.
Вариант № 5 Вариант № 6
1. 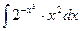 ; 1.
; 1. 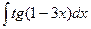 ;
;
2.  ; 2.
; 2. 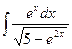 ;
;
3. 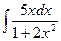 ; 3.
; 3. 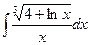 ;
;
4.  . 4.
. 4. 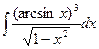 .
.
Вариант № 7 Вариант № 8
1. 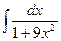 ; 1.
; 1. 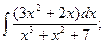
2. 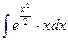 ; 2.
; 2. 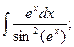
3. 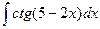 ; 3.
; 3. 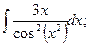
4.  . 4.
. 4. 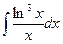 .
.
Вариант № 9 Вариант № 10
1. 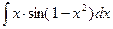 ; 1.
; 1. 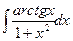 ;
;
2. 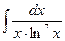 ; 2.
; 2. 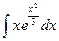 ;
;
3. 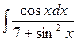 ; 3.
; 3. 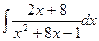 ;
;
4. 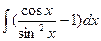 ; 4.
; 4. 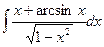 .
.
Задание 2
Проинтегрировать, выбрав нужный метод интегрирования.
Вариант № 1 Вариант № 2
1. 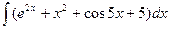 ; 1.
; 1.  ;
;
2. 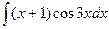 ; 2.
; 2. 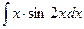 ;
;
3.  ; 3.
; 3. 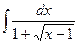 ;
;
4. 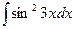 . 4.
. 4. 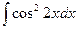 .
.
Вариант № 3 Вариант № 4
1.  ; 1.
; 1. 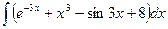 ;
;
2. 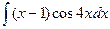 ; 2.
; 2. 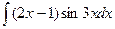 ;
;
3. 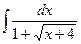 ; 3.
; 3. 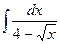 ;
;
4. 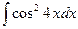 . 4.
. 4. 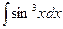 .
.
Вариант № 5 Вариант № 6
1. 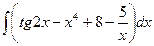 ; 1.
; 1. 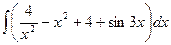 ;
;
2. 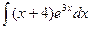 ; 2.
; 2.  ;
;
3. 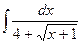 ; 3.
; 3. 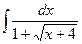 ;
;
4. 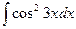 . 4.
. 4. 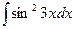 .
.
Вариант № 7 Вариант № 8
1. 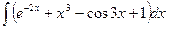 ; 1.
; 1.  ;
;
2. 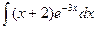 ; 2.
; 2. 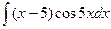 ;
;
3. 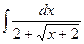 ; 3.
; 3.  ;
;
4. 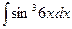 . 4.
. 4. 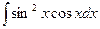 .
.
Вариант № 9 Вариант № 10
1. 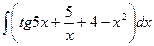 ; 1.
; 1. 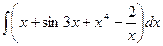 ;
;
2. 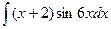 ; 2.
; 2. 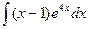 ;
;
3.  ; 3.
; 3. 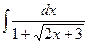 ;
;
4. 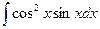 . 4.
. 4. 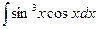 .
.
Задание 3
Вычислить определённый интеграл.
Варианты
1. 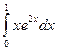 ; 2.
; 2. 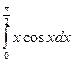 ; 3.
; 3. 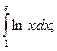 4.
4. 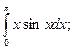
5. 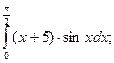 6.
6. 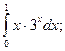 7.
7. 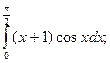 8.
8.  9.
9. 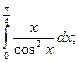 10.
10. 
Задание 4
Вычислить площадь фигуры, ограниченной данными линиями.
Варианты.
1. ху = 6, х + у = 7; 6. у = 2х – х2, у = 0;
2. у= 3х – х2, у = 0; 7. у = 6х – х2, у = 0;
3. ху = 8, х + у = 6; 8. у = 1 – х2, у = 0, х < 0;
4. у = 4х – х2, у = 0; 9. у = 9 – х2, х >0, у = 0;
5. у = 4 – х2, у = 0, х > 0; 10. у = 25 – х2, у = 0, х <0.
Задание 5
По формулам трапеций и парабол (Симпсона) приближенно вычислить интеграл.
Варианты
1. 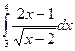 ,
, 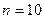 ; 6.
; 6. 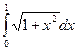 ,
, 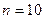 ;
;
2. 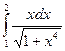 ,
, 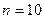 ; 7.
; 7. 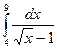 ,
, 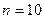 ;
;
3. 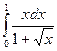 ,
, 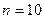 ; 8.
; 8. 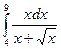 ,
, 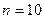 ;
;
4.  ,
, 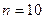 ; 9.
; 9. 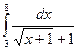 ,
, 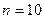 ;
;
5. 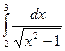 ,
, 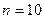 ; 10.
; 10. 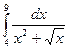 ,
, 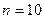 .
.
Решение типовых задач
Задание 1
Непосредственным интегрированием найти следующие интегралы:
а) 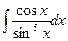 ; б)
; б) 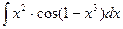 ;
;
в) 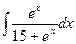 ; г)
; г) 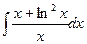 .
.
Задание 2
Проинтегрировать, выбрав нужный метод интегрирования.
а) 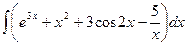 ;
;
б) 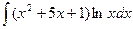 ;
;
в) 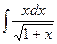 ;
;
г) 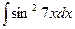 .
.
Задание 3
Вычислить определённый интеграл  .
.
Задание 4
Вычислить площадь фигуры, ограниченной линиями:
xy = 3, y + x = 4.
Задание 5
По формулам трапеций и парабол (Симпсона) приближенно вычислить интеграл 
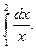
Сведения из теории
Таблица интегралов
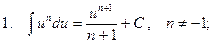
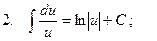
3. 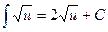 ;
;
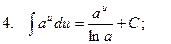

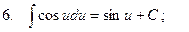
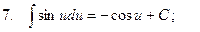
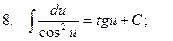
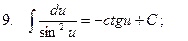
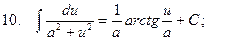
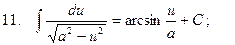
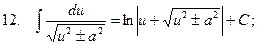
Свойства неопределённого интеграла
1. 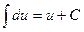 ;
;
2.  , k – число;
, k – число;
3. 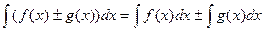 .
.
Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к табличному интегралу, называется непосредственным интегрированием.
При сведении интегралов к табличным, используются следующие свойства дифференциала:
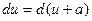 , a – число,
, a – число,
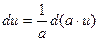 , a
, a 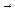 0 – число, а также преобразования:
0 – число, а также преобразования:
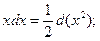

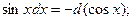
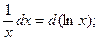


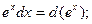
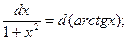
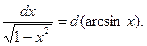
Пример выполнения задания 1
Непосредственным интегрированием найдём следующие интегралы:
а) 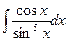 ; б)
; б)  ;
;
в) 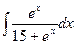 ; г)
; г) 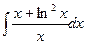 .
.
Сведем данные интегралы к табличным.
а)  .
.
б) 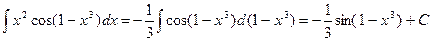 .
.
в) 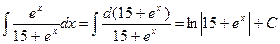 .
.
г)
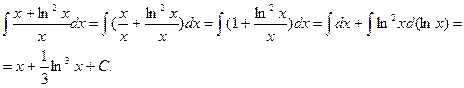
Пример выполнения задания 2
Проинтегрируем, выбрав нужный метод интегрирования.
а) 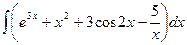 ;
;
б) 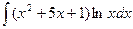 ;
;
в) 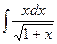 ;
;
г) 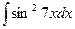 .
.
Решение.
а) 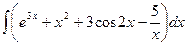 .
.
Используя метод непосредственного интегрирования и свойства неопределённого интеграла, заданный интеграл преобразуем к сумме табличных интегралов.
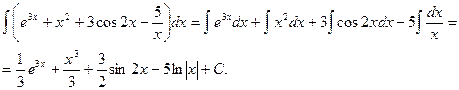
б)  .
.
Применим метод интегрирования по частям:
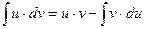 .
.
Обозначим: 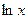 =
= 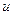 ,
, 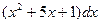 =
= 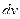 , найдем
, найдем 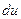 и
и 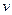 и подставим полученные выражения в формулу интегрирования по частям:
и подставим полученные выражения в формулу интегрирования по частям:
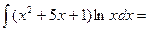
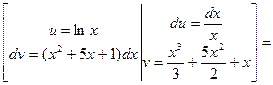
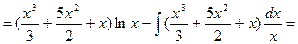
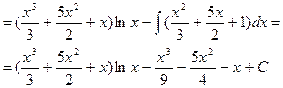 .
.
в) 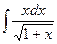 .
.
Применим метод замены переменной, обозначив 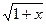 за переменную
за переменную 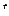 .
.
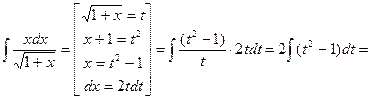
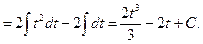
Вернёмся к переменной х:
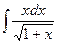
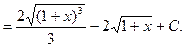
г) 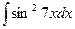 .
.
Применим формулу понижения степени синуса: 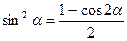 .
.

Пример выполнения задания 3
Вычислим определенный интеграл 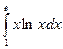 .
.
Решение.
Применим метод интегрирования по частям в определённом интеграле.

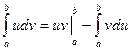 .
.

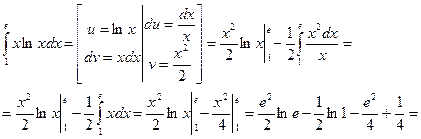


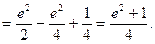


Ответ: 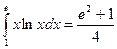 .
.
Пример выполнения задания 4
Вычислим площадь фигуры, ограниченной следующими линиями:
xy = 3, y + x = 4.
Решение.
Строим в прямоугольной системе координат данные линии.


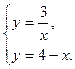
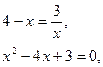
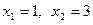 .
.
 =4 – 3 ln3 (ед2).
=4 – 3 ln3 (ед2).
Ответ: S = 4 – 3 ln 3 (ед2).
Пример выполнения задания 5
По формулам трапеций и парабол (Симпсона) приближённо вычислим интеграл 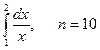 .
.
Решение.
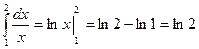 – точное значение интеграла.
– точное значение интеграла.
Применим формулу трапеций:
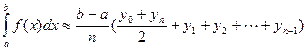 ,
,
В нашей задаче 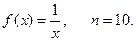
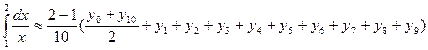 .
.
Составим таблицу значений:
| х | 
| х | 
|
| х0=1,0 | у0=1,00000 | х6=1,6 | у6=0,62500 |
| х1=1,1 | у1=0,90909 | х7=1,7 | у7=0,58824 |
| х2=1,2 | у2=0,83333 | х8=1,8 | у8=0,55556 |
| х3=1,3 | у3=0,76923 | х9=1,9 | у9=0,52632 |
| х4=1,4 | у4=0,71429 | х10=2,0 | у10=0,50000 |
| х5=1,5 | у5=0,66667 |
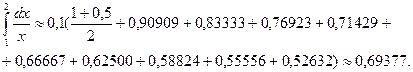
Применим формулу Симпсона:

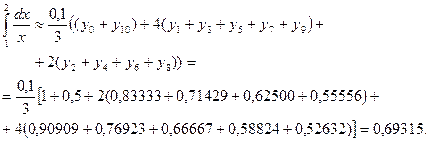
Сравнивая приближённые значения интеграла со значением, полученным по формуле Ньютона-Лейбница,  , мы видим, что формула Симпсона дает более точный результат, чем формула трапеций.
, мы видим, что формула Симпсона дает более точный результат, чем формула трапеций.
Модуль 6
Интегральное исчисление функций нескольких переменных
Задачи для решения
Задание 1
Вычислить двойной интеграл по области интегрирования D.
Варианты
1. 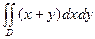 , где область D ограничена линиями
, где область D ограничена линиями
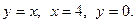
2. 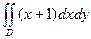 , где область D ограничена линиями
, где область D ограничена линиями
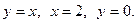
3.  , где область D ограничена линиями
, где область D ограничена линиями
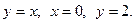
4. 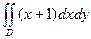 , где область D ограничена линиями
, где область D ограничена линиями

5. 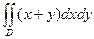 , где область D ограничена линиями
, где область D ограничена линиями
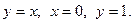
6. 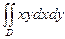 , где область D ограничена линиями
, где область D ограничена линиями
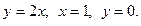
7. 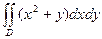 , где область D ограничена линиями
, где область D ограничена линиями
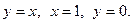
8. 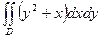 , где область D ограничена линиями
, где область D ограничена линиями
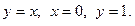
9. 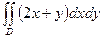 , где область D ограничена линиями
, где область D ограничена линиями

10.  , где область D ограничена линиями
, где область D ограничена линиями

Задание 2
С помощью двойного интеграла вычислить площадь фигуры, ограниченной данными линиями.
Варианты.
1. х2+ у2 ≥ 1, х2 + у2 ≤ 4;
2. х2+ у2≥ 1, х2+ у2≤ 4; х ≥ 0, у ≥ 0;
3. х2+ у2 ≥ 1, х2 + у2≤ 9;
4. х2+ у2 ≥ 1, х2+ у2 ≤ 9; х ≥ 0, у ≥ 0;
5. х2+ у2 ≥ 4, х2+ у2 ≤ 9;
6. х2+ у2 ≥ 4, х2+ у2 ≤ 9; х ≥ 0, у ≥ 0;
7. х2+ у2 ≥ 9; х2+ у2 ≤ 16;
8. х2+ у2 ≥ 9, х2+ у2 ≤ 16; х ≥ 0, у ≥ 0;
9. х2+ у2 ≥ 4, х2+ у2 ≤ 16;
10. х2+ у2 ≥ 4, х2+ у2 ≤ 16; х ≥ 0, у ≥ 0.
Задание 3
С помощью тройного интеграла найти объём тела, ограниченного данными поверхностями.
Варианты
1. z = 4 - х2- у2, z =0;
2. z =х2+ у2+ 1, z =5;
3. z = х2+ у2, z = 9;
4. z2 = х2+ у2, z = 2;
5. z = х2+ у2, z =4;
6. z = 9 - х2- у2, z =0;
7. z2 = х2+ у2, z = 3;
8. z =х2+ у2+ 2, z =6;
9. z = 5 - х2- у2, z =1;
10. z = 7 - х2- у2, z =3;
Решение типовых задач
Задание 1
Вычислить двойной интеграл по области интегрирования D.
а) 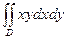 , где область D ограничена линиями
, где область D ограничена линиями
у = х, у = 2, х=0.
б)  , где область D ограничена линиями:
, где область D ограничена линиями:
х2+ у2 ≥ 1, х2+ у2 ≤ 4, 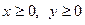 .
.
Задание 2
С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями:
а) у = х2 + 1, у = х + 3;
б) ρ = 2 sin φ, ρ = 4 sin φ.
Задание 3
С помощью тройного интеграла найти объём тела, ограниченного поверхностями:
а) z = х2+ у2, z = 1.
б) х+ у+ z = 1, х = 0, у = 0, z = 0.
Пример выполнения задания 1
а) Вычислим двойной интеграл 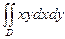 по области интегрирования D, ограниченной линиями у = х, у = 2, х = 0.
по области интегрирования D, ограниченной линиями у = х, у = 2, х = 0.
Решение
Строим область интегрирования D в прямоугольных координатах и расставляем пределы интегрирования в повторном интеграле.

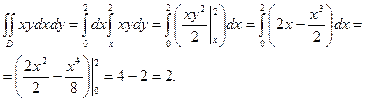
Ответ: 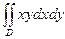 = 2.
= 2.
б) Вычислим интеграл 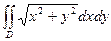 , где область D
, где область D
 ограничена линиями х2+ у2 ≥ 1,
ограничена линиями х2+ у2 ≥ 1,
х2+ у2 ≤ 4, 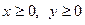 .
.
Строим область интегрирования D.
По области D определяем, что
данный интеграл следует вычислять
в полярных координатах.
Приведём к полярным координатам
уравнение окружности 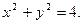
Формулы перехода к полярным координатам: 
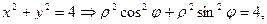
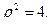
Уравнение окружности 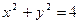 в полярных координатах
в полярных координатах  . Аналогично уравнение окружности х2+ у2 = 1 в полярных
. Аналогично уравнение окружности х2+ у2 = 1 в полярных
координатах 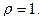
Область D ограничена линиями 
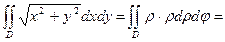
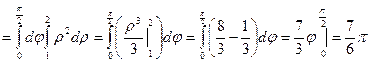 .
.
Ответ: 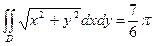 .
.
Пример выполнения задания 2
а) С помощью двойного интеграла вычислим площадь фигуры, ограниченной линиями: у = х2 + 1, у = х + 3.
Решение.
В прямоугольных координатах площадь области D: 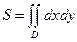
Строим в прямоугольных координатах линии у = х2 +1 и у = х+3.


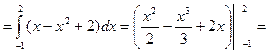
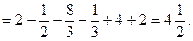
Ответ: 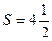 (ед2).
(ед2).
б) С помощью двойного интеграла вычислим площадь фигуры, ограниченной линиями, заданными в полярных координатах:
ρ = 2 sin φ, ρ = 4 sin φ.
Решение.
Линии ρ = 2 sin φ, ρ = 4 sin φ представляют собой окружности диаметров 2 и 4, центры которых лежат в точках (0,1) и (0,2) соответственно. Площадь фигуры, заключённой между этими окружностями вычисляем по формуле:
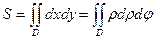


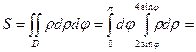



Ответ: 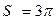 (ед2).
(ед2).
Пример выполнения задания 3
С помощью тройного интеграла найдём объём тела, ограниченного поверхностями z = х2+ у2, z = 1.
Данное тело ограничено плоскостью z = 1 и параболоидом
z = х2+ у2. Найдем объём тела через тройной интеграл, используя цилиндрические координаты.



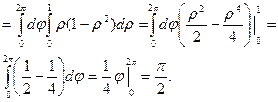
Ответ: 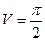 (ед3).
(ед3).
I II семестр
Вопросы
1. Обыкновенные дифференциальные уравнения. Основные понятия. Задача Коши.
2. Дифференциальные уравнения первого порядка с разделяющимися переменными.
3. Линейные дифференциальные уравнения первого порядка.
4. Однородные дифференциальные уравнения первого порядка.
5. Уравнения первого порядка в полных дифференциалах.
6. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
7. Нахождение общего решения линейного однородного дифференциального уравнения с постоянными коэффициентами по корням его характеристического уравнения
8. Решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами методом неопределенных коэффициентов.
9. Общие сведения о числовых рядах. Абсолютная и условная сходимость числовых рядов.
10. Необходимые признаки сходимости числовых рядов.
11. Достаточные признаки сходимости числовых рядов (признак сравнения, признак Даламбера, радикальный признак Коши, интегральный признак Коши, признак Лейбница).
12. Степенные ряды. Теорема Абеля.
13. Область и радиус сходимости степенного ряда.
14. Общие сведения о тригонометрических рядах и периодических функциях.
15. Ряд Фурье. Достаточное условие разложимости функций в ряд Фурье.
16. Нахождение коэффициентов тригонометрического ряда для функций с периодом 2π.
17. Разложение в ряд Фурье функций с периодом 2l.
18. Разложение функций в ряд Фурье четным и нечетным образом.
Модуль 7
Дифференциальные уравнения
Задачи для решения
Задание 1
Проинтегрировать дифференциальные уравнения. Найти частные решения, удовлетворяющие соответствующим начальным условиям.
Варианты
1. a) 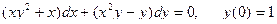 ;
;
б) 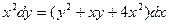 ;
;
в) у' + ycosx = cosx , y(0) = -2;
г) 
2. а) y' ctgx+ y = 2, y(0) = 1;
б) 2xy' (x2 + y2) = y(y2 + 2x2);
в) xy' - x2sinx = y;
г) (2y – x + 3y2)dy + (3x2 – 2x - y)dx = 0;
3. а) 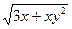 dx+ 2ху dу= 0, y(4) = 1;
dx+ 2ху dу= 0, y(4) = 1;
б) 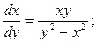
в) 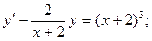
г) 3 x2 (1 + lny)dx – (2y – 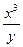 )dy = 0;
)dy = 0;
4. а) y' tgx = ylny, y(  ) = е;
) = е;
б) 
в) 
г) (2y - 3)dx + (2x + 3y2)dy = 0;
5. а) (xy +х )dx - (x2+1)dy = 0, y(1) = 0;
б) xy' cos(y/x) = y cos(y/x) – x;
в) y' cosx + ysinx = 1;
г) (2xy + 1)dx + (x2-y2)dy = 0;
6. а) 

б) 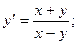
в) y' + y tgx= 2x cosx;
г) 3x2 ey dx + (x3ey + 1)dy = 0;
7. а) xy' – y2 = 1; y(1) = 1;
б) 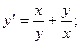
в) y' + 2xy = 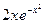 ;
;
г) e- y dx + (2y – xe- y)dy = 0;
8. а) 3ex sinydx – (ex + 1) cosydy = 0, y(0) = π/2;
б) 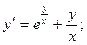
в) 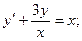
г) (12x + 5y – 9) dx + (5x + 2y – 4) dy = 0;
9. а) xy y' = 1 – x2 , y(1) = 2;
б) 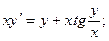
в) 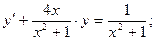
г) (x + lny)dx + (1 + 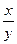 + siny)dy = 0;
+ siny)dy = 0;
10. а) (xy2 + x) dx + (x2y - y)dy = 0, 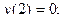
б) x3у' = у(х2 + у2);
в) 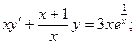
г) 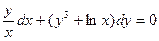 .
.
Задание 2
Найти общее решение линейных дифференциальных уравнений второго порядка с постоянными коэффициентами.
Варианты
1. а) у'' + 7у' + 10 = 0;
б) у'' + 12у' + 36у = 0;
в) 6у'' + 5у' + 2у = 0;
г) у'' + 4у' = 9х + 5;
д) у'' + 8у' + 15у = 2cos3x;
е) у'' + 9у = 5е2х.
2. а) у'' + 5у' + 4у = 0;
б) у'' + 10у' + 25у = 0;
в) 2у'' – 5у' + 6у = 0;
г) у'' + 9у' = 2х + 1;
д) у'' + у = 3е6х;
е) у'' + 2у' – 3у = 4sin5x.
3. а) у'' + 9у' + 18у = 0;
б) у'' – 2у' + у = 0;
в) 3у'' – 5у' + 3у = 0;
г) у'' + 10у' = 6х – 2;
д) у'' + 4у' = 2е5х;
е) у'' + 3у' – 4у = 8 sin2x.
4. а) у'' + 8у' + 7у = 0;
б) у'' – 8у' + 16у = 0;
в) 3у'' + 5у' + 3у = 0;
г) у'' + 4у' = 3х + 5;
д) у'' + 16у' = 3е-4х;
е) у'' + 4у' – 5у = 4cos2x.
5. а) у'' + 10у' + 21у = 0;
б) у'' + 6у' + 9у = 0;
в) 2у'' – 5у' + 4у = 0;
г) у'' + 24у' = 3х – 2;
д) у'' + 25у = 6е7х;
е) у'' – у' – 2у = 5sin6x.
6. а) у'' + 6у' + 8у = 0;
б) у'' + 4у' + 4у = 0;
в) 5у'' – 4у' + у = 0;
г) у'' + 25у' = 9х – 2;
д) у'' + 36у' = 5е4х;
е) у'' + 2у' – 8у = 4cos3x.
7. а) у'' + 8у' + 15у = 0;
б) 3у'' + 6у' + 3у = 0;
в) 3у'' + 4у' + 2у = 0;
г) у'' + 36у' = 8х – 3;
д) у'' + 49у = 7е-3х;
е) у'' + 3у' – 10у = 5cos3x – sin3x.
8. а) у'' +у' – 6у = 0;
б) 9у'' – 6у' + у = 0;
в) у'' + 4у' + 5у = 0;
г) у'' + 49у' = 5х + 4;
д) у'' + 64у = 8е-2х;
е) у'' – у' – 6у = 4sin2x + 3cos2x.
9. а) у'' + 5у' + 6у = 0;
б) у'' 6у' + 9у = 0;
в) у'' + 4у' + 8у = 0;
г) у'' + 8у' = 6х + 2;
д) у'' + 81у = 5е3х ;
е) у'' – 2у' – 3у = 5sin3x.
10. а) у'' + 7у' + 12у = 0;
б) у'' + 8у' + 16у = 0;
в) у'' – 4у' + 20у = 0;
г) у'' +16у' = 2х – 1;
д) у'' + 100у = 4е2х;
е) у'' + у' – 12у = 3cos2x.
Задание 3
Решить систему дифференциальных уравнений.
Варианты
1. 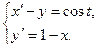 2.
2. 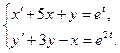
3. 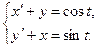 4.
4. 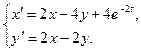
5.  6.
6. 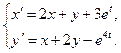
7.  8.
8. 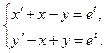
9. 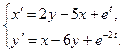 10.
10. 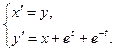
Решение типовых задач
Задание 1
Проинтегрировать дифференциальные уравнения. Найти частные решения, удовлетворяющие соответствующим начальным условиям.
а) х(1 + у2) + у(1 + х2) у' = 0 , 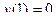 ;
;
б) 2x2dy = (x2 + y2)d;
в) 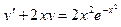 ;
;
г) 2xcos2ydx + (2y – x2sin2у)dy = 0, у(0)=0.
Задание 2
Найти общее решение линейных дифференциальных уравнений.
а) 2y'' + 5у' + 2у = 0;
б) у'' + 6у' + 13у = 0;
в) у'' – 8у' + 16у = 0;
г) у'' – 5у' + 6у = 13sin3x.
Задание 3
Решить систему дифференциальных уравнений
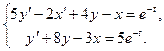
Сведения из теории
Дифференциальные уравнения первого порядка
Дифференциальным называется уравнение, связывающее независимую переменную х, неизвестную функцию у и производную у' или дифференциал неизвестной функции.
По определению дифференциала 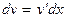 , следовательно,
, следовательно,
 .
.
Общий вид дифференциального уравнения 1-го порядка:
F(x,y,y') = 0, или P(x,y)dx + Q(x,y)dy = 0.
Решением дифференциального уравнения называется всякая функция у = φ(х), которая, будучи подставлена в уравнение, обратит его в тождество, т.е. F(x,φ(x),φ'(x)) = 0.
Задачей Коши для уравнения 1-го порядка называется задача определения частного решения уравнения F(x,y,y') = 0 при заданном начальном условии у(x0) = y0. Существует несколько типов дифференциальных уравнений.
Уравнения с разделяющимися переменными
Если уравнения вида P(x,y)dx + Q(x,y)dy = 0 после преобразования может быть записано в виде
ƒ1(x)ƒ2(y)dx + q1(x) q2(y)dy = 0,
то оно называется уравнением с разделяющимися переменными.
Однородные дифференциальные уравнения
Дифференциальное уравнение, которое можно преобразовать к виду 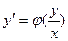 , называется однородным. Подстановка
, называется однородным. Подстановка  , где
, где 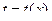 новая неизвестная функция, приводит однородное уравнение к уравнению с разделяющимися переменными.
новая неизвестная функция, приводит однородное уравнение к уравнению с разделяющимися переменными.
Линейные дифференциальные уравнения
Уравнение вида y' + p(x)y = q(x), где p(x) и q(x) непрерывные функции x, называется линейным.
Линейные уравнения решают методом, при котором делается замена 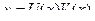 . Одну из двух новых неизвестных функций можно выбирать произвольно. Этой подстановкой линейные уравнения приводятся к двум уравнениям с разделяющимися переменными.
. Одну из двух новых неизвестных функций можно выбирать произвольно. Этой подстановкой линейные уравнения приводятся к двум уравнениям с разделяющимися переменными.
Уравнение в полных дифференциалах
Уравнение P(x,y)dx + Q(x,y)dy = 0 называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции U(x,y):
P(x,y)dx + Q(x,y)dy = dU(x,y).
Для этого необходимо и достаточно, чтобы выполнялось: 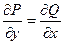 .
.
Пример выполнения задания 1
а) Решим уравнение х(1 + у2) + у(1 + х2) у' = 0 с начальными условиями 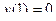 .
.
Решение.
Запишем производную через отношение дифференциалов  . Получим:
. Получим:
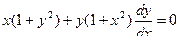 .
.
Представим данное уравнение в виде:
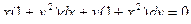 ,
,
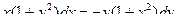 .
.
Разделив обе части этого уравнения на произведение 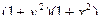 ,
,
получим уравнение с разделяющимися переменными:
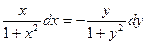 .
.
Интегрируя это уравнение, находим его общее решение:
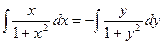 ,
,
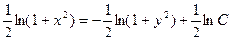 ,
,
(константу С удобно записать в виде  ),
),
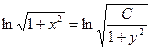 .
.
Получили общее решение дифференциального уравнения:
 .
.
Найдём частное решение, соответствующее начальным условиям 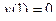 :
:
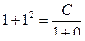 . Отсюда:
. Отсюда:  .
.
Частное решение дифференциального уравнения:
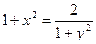 .
.
б) Проинтегрируем однородное уравнение
2x2dy = (x2 + y2)dx.
Решение.
Разделив обе части равенства на x2 , получим:
 .
.
Положив в нем 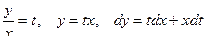 , получим:
, получим: 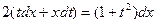 , или
, или 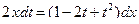 .
.
Это уравнение с разделяющимися переменными.
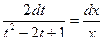 . Интегрируем:
. Интегрируем:

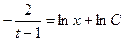 .
.
Возвращаясь к переменной у через обратную замену, получим общий интеграл исходного уравнения:
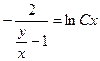 .
.
Эту функцию можно преобразовать к виду:  .
.
в) Проинтегрируем линейное уравнение 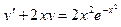 .
.
Решение.
Положим 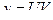 ,
, 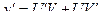 , подставим y и y' в данное
, подставим y и y' в данное
уравнение:
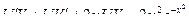 ,
,
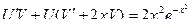 .
.
Положим 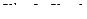 , (*)
, (*)
тогда  . (**)
. (**)
Решим первое уравнение:
 ,
, 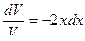 , проинтегрировав, получим:
, проинтегрировав, получим:
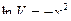 , или
, или 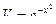 .
.
Подставив V в уравнение (**) , получим:
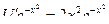 ,
,
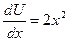 ,
, 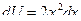 , откуда
, откуда 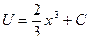 .
.
Общее решение уравнения:
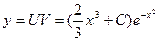 .
.
г) Найдём общее решение дифференциального уравнения 2xcos2ydx + (2y – x2sin2у)dy = 0 и частное решение по данным начальным условиям 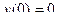 .
.
Решение.
P(x,y) = 2xcos2y , Q(x,y) = 2y – x2sin2y.
Так как 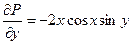 ,
, 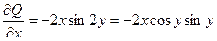 ,
,
из равенства частных производных вытекает, что это – уравнение в полных дифференциалах, т.е. существует такая функция U(x,y), для которой

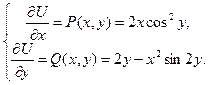
Проинтегрировав первое равенство по х, найдем U(x,y) c точностью до произвольной функции от y:
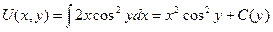 .
.
Чтобы определить С(y), продифференцируем найденную функцию по у:
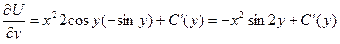 ,
,
приравнивая её к уже известному значению 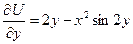 , получим:
, получим: 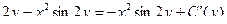 , таким образом,
, таким образом, 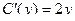 . Проинтегрировав, найдём С(у).
. Проинтегрировав, найдём С(у).
С(y) = y2 + C1.
U(x,y) = x2cos2y +у2 + C1 .
Общий интеграл уравнения: y2 + x2cos2y = C.
Подставив в общий интеграл начальные значения, определим С :
 , следовательно, C = 0.
, следовательно, C = 0.
Частное решение исходного уравнения имеет вид:
y2 + x2cos2y = 0.
Сведения из теории
Дифференциальные уравнения высших порядков
Дата: 2018-12-28, просмотров: 495.