При неустановившемся течении вязкой несжимаемой жидкости в поле сил тяжести уравнение Бернулли, выражающее закон сохранения механической энергии потока на участке между двумя сечениями 1 и 2, имеет вид:

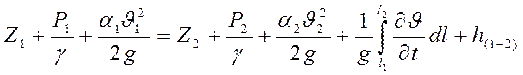. (52)

В этом уравнении каждый из членов имеет линейную размерность.

Первый член уравнения – Z определяет высоту положения центра тяжести живого сечения потока над произвольной горизонтальной плоскостью и называется геометрической высотой или геометрическим напором. Он характеризует удельную (единицы веса жидкости) энергию положения в поле сил тяжести.

Второй член уравнения – P/g соответствует гидростатическому давлению в данной точке потока и называется пьезометрическим напором (или высотой). Пьезометрический напор характеризует удельную потенциальную энергию давления в данном сечении потока.

Третий член уравнения 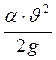 называется скоростной высотой или скоростным напором, он определяет удельную кинетическую энергию жидкости в данном сечении потока.

J – средняя скорость течения жидкости в живом сечении потока;

a – коэффициент кинетической энергии (коэффициент Кориолиса), учитывающий неравномерность распределения скорости в живом сечении потока. При ламинарном режиме движения a=2; при развитом турбулентном режиме a=1,05 ¸ 1,1;

g – удельный вес жидкости;

Р – давление в центре тяжести рассматриваемого сечения потока.

Последний член уравнения Бернулли h_w(1-2) представляет собой потерю полного напора на преодоление сопротивлений на между рассматриваемыми сечениями 1 и 2.

В отличие от уравнения Бернулли для установившегося течения жидкости уравнение Бернулли для неустановившегося течения (52) содержит член: 

,                                          

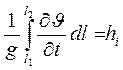который называется инерционным напором.

Если поперечное сечение трубы постоянно, т.е. ,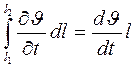

т.к. 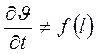;  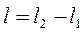длина рассматриваемого участка трубопровода;

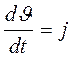– ускорение жидкости в рассматриваемом участке трубопровода, то уравнение (1) приводится к виду:

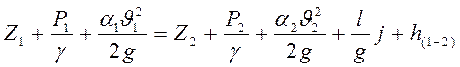                 .          (53)

Уравнение (53) широко используется для расчета и анализа переходных процессов в гидросистемах.

Переходный процесс – это процесс установления установившегося движения (стационарного течения) после переключения запорно-регулирующих устройств (распределителей, дросселей, клапанов и т.д.) в гидросистеме. 

Решение уравнения (53) для различных случаев неустановившихся течений жидкости в гидросистемах показывает, что после переключения запорно-регулирующих органов скорость течения жидкости, а также скорости движения исполнительных органов гидроприводов изменяются по закону гиперболического тангенса:

,

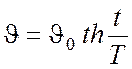где 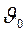– скорость установившегося движения жидкости или исполнительного органа гидропривода;

Т – постоянная времени переходного процесса.

Рис. 4.8. Переходный процесс в гидроситемах.