(графический метод расчета)

Обычной задачей расчета трубопровода с параллельными ветвями (рис.4.4) является определение расхода жидкости в каждой из параллельных ветвей при заданном общем расходе Q₀.

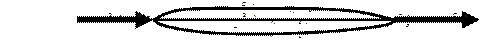
Рис.4.4. Трубопровода с параллельными ветвями

Для решения этой задачи используются расчетные соотношения для определения потерь давления в каждой из параллельных ветвей:

Δp=(р_А–р_В)=Δp_li +Δp_мi = 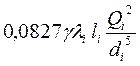+ 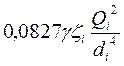, (48)

где Δp_li, Δp_мi – потери давления, соответственно, по длине трубопровода и на местных сопротивлениях соответствующей (i-ой) ветви;

 l_i, d_i – длина, диаметр трубопровода соответствующей ветви;

 Q_i – расход жидкости в соответствующей параллельной ветви;

  λ_i, ζ_i – коэффициенты гидравлического трения и местного сопротивления трубопровода соответствующей ветви.

Система уравнений (48) содержит 3 уравнения (для данной схемы – рис.1) с 4 неизвестными: 3 искомых расхода   и Δp.

Дополнительным (4-ым) уравнением является задание суммарного расхода:

Σ Q_i= Q₀, (49)                              

которое и замыкает систему уравнений (48).

Аналитическое решение системы уравнений (48, 49) в принципе возможно, в результате чего можно определить Q_i  и Δp. Однако в тех случаях, когда коэффициенты λ_i и ζ_i зависят от числа Рейнольдса, или в конечном счете, от расхода  Q_i , то решение становится чрезвычайно громоздким и требует сложных итеративных процедур, т.к. система уравнений (48, 49) представляет собой систему сложных, неявных уравнений относительно Q_i.

Во многих случаях удобен графический метод расчета параллельной трубопроводной системы – метод характеристик. В этом случае на одном графике Δp = f(Q_i) с использованием выражений (48) строятся характеристики каждой из параллельных ветвей. Характеристика представляет собой зависимость потерь давления от расхода соответствующей параллельной ветви.

Затем полученные характеристики параллельных ветвей суммируются согласно соотношению (48) путем сложения абсцисс (расходов) кривых при одинаковых ординатах (Δp). Полученная в результате такого суммирования характеристика может рассматриваться как характеристика эквивалентной трубы, заменяющей совокупность параллельных ветвей.

       Схема решения приведена на рисунке.

Рис.4.5. Зависимость расхода Q от потерь давления Δp в трубопроводе с параллельными ветвями

Отложив на оси абсцисс суммарный расход Q₀ ,  далее построением определяем Q₁,Q₂, Q₃, а также можно определить Δp_isk.

Использование графического метода особенно удобно, когда общий расход жидкости Q₀  часто изменяется в процессе эксплуатации трубопроводной системы.