Обычно заземлители погружают в землю на относительно небольшую глубину, при которой поверхность земли оказывает влияние на электрическое поле, искажая линии тока (рис. 3.2, 3.3).
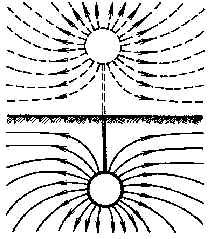
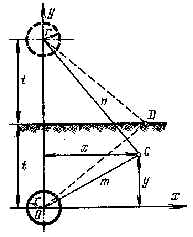
Рис.3.2. Поле растекания тока Рис.3.3. Шаровой заземлитель вблизи
шарового заземлителя и его поверхности земли и его зеркалное
и его зеркального отображения отображение
В этом случае расчет потенциалов осуществляется методом зеркального отображения: потенциал jс в некоторой точке С будет равен сумме потенциалов j д и j ф, создаваемых в этой точке полями токов, стекающих как с действительного, так и с фиктивного заземлителей, В:
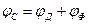
С учетом уравнения 3.1 можно записать:
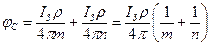 ,
,
где m и n - расстояния от центров действительного и фиктивного заземлителей до точки С:
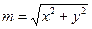 ,
,
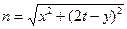 .
.
Если нас интересуют потенциалы точек, лежащих на поверхности земли, то для каждой такой точки, например точки D (рис. 2.3),
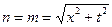 (3.3)
(3.3)
а уравнение, определяющее ее потенциал, т. е. уравнение потенциальной кривой для точек на поверхности земли имеет вид:
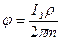 (3.4)
(3.4)
или
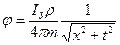 (3.5)
(3.5)
Потенциал шарового заземлителя вблизи поверхности земли j з, В, т. е. максимальный потенциал, будет при y = 0 и, следовательно, при х = r (рис. 3.3):
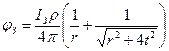 (3.6)
(3.6)
Если 4t2 >> r (так обычно бывает на практике), это уравнение примет вид:
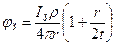 (3.7)
(3.7)
Полушаровой заземлитель
Шаровой заземлитель на поверхности земли, т. е. заглубленный так, что его центр находится на уровне земли (рис. 2.4), называется полушаровым заземлителем.
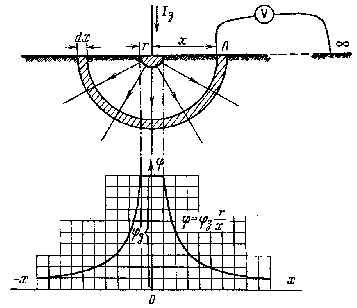
Рис. 3.4. Распределение потенциала на поверхности земли вокруг полушарового заземлителя
Для такого заземлителя уравнение потенциальной кривой на поверхности земли (так же как и в объеме земли) можно получить из (3.5), приняв t = 0. Тогда:
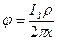 (3.8)
(3.8)
(Это же выражение можно получить и другим путем, используя подход, как при выводе уравнения потенциальной кривой шарового заземлителя. )
Потенциал полушарового заземлителя j з, В, при радиусе заземлителя х = r, м, определяется из уравнения:
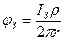 (3.9)
(3.9)
Разделив (2.8) на (2.9), получим:
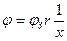 (3.10)
(3.10)
Обозначив произведение постоянных j з и r через k, получим уравнение равносторонней гиперболы:
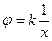 (3.11)
(3.11)
Следовательно, потенциал на поверхности земли вокруг полушарового заземлителя изменяется по закону гиперболы, уменьшаясь от максимального значения j з до нуля по мере удаления от заземлителя (рис. 3.4). Следует отметить, что в реальных условиях, когда грунт неоднороден, изменение потенциала при удалении от заземлителя будет происходить не по гиперболе, а по какой-либо другой кривой.
Стержневой заземлитель
Рассмотрим стержневой вертикальный заземлитель круглого сечения длиной l, м, и диаметром d, м, погруженный в землю так, чтобы его верхний конец был на уровне земли (рис. 2.5). По заземлителю стекает ток Iз, А. Требуется записать выражение для расчета потенциала точек на поверхности земли и потенциала заземлителя.
Разбиваем заземлитель по длине на бесконечно малые участки длиной каждый dy и уподобляем их элементарным шаровым заземлителям диаметром dy, м. С каждого такого участка в землю стекает ток, А
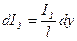 ,
,
который обусловливает возникновение элементарного потенциала d j в любой точке земли. Для точки А на поверхности земли
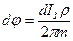
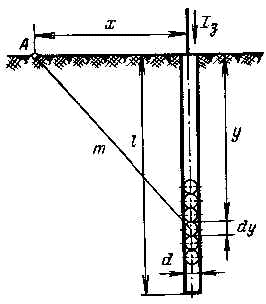
Рис. 2.5. Стержневой заземлитель
С помощью соответствующих подстановок и интегрируя по всей длине стержневого заземлителя (от 0 до l), получим уравнение потенциальной кривой:
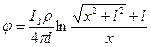 (3.12)
(3.12)
Потенциал заземлителя j з, В, определяется при х = 0,5 d, м, т, е.
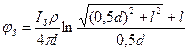
Обычно на практике 0,5d << l, следовательно, первым слагаемым под корнем можно пренебречь. Тогда выражение для расчета потенциала стержневого заземлителя примет вид:
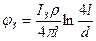 (3.13)
(3.13)
Дисковый заземлитель
Дисковый заземлитель – это круглая пластина диаметром D, м, лежащая на земле (рис. 3.6). Распределение потенциала на поверхности земли вдоль радиуса диска описывается уравнением:
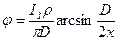 (3.14)
(3.14)
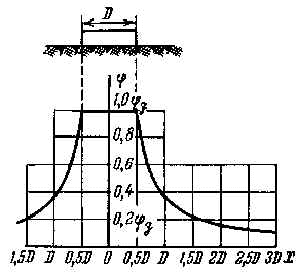
Рис.3.6. Распределение потенциала на поверхности земли вокруг дискового заземлителя
Потенциал дискового заземлителя (при х = 0,5D, м):
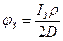 . (3.15)
. (3.15)
Дата: 2019-02-02, просмотров: 414.