Шаровой заземлитель в практике, как правило, не применяется. Однако на его примере удобно рассмотреть процессы возникновения и распределения потенциалов на поверхности земли.

Пусть мы имеем шаровой заземлитель радиусом r, м, погруженный в землю на бесконечно большую глубину (так глубоко, что можно пренебречь влиянием поверхности земли). Через этот шар в землю стекает ток I_з, А, который подается к заземлителю с помощью изолированного проводника (рис. 3.1). Требуется получить уравнение для потенциала j , В, в некоторой точке объема земли C, отстоящей от центра заземлителя на расстоянии x, м, или, иначе говоря, уравнение потенциальной кривой.

Поскольку принято, что земля однородна, ток в земле будет растекаться от шара равномерно и симметрично во все стороны (по радиусам шара) и плотность его в земле будет убывать по мере удаления от заземлителя. На расстоянии x, м, от центра шара плотность тока d, А/м².

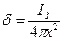
В объеме земли, где проходит ток, возникает так называемое поле растекания тока. Теоретически оно простирается до бесконечности. Однако в действительных условиях уже на расстоянии 20 м от заземлителя сечение слоя земли, через который проходит ток, оказывается столь большим, что плотность тока здесь практически равна нулю. Следовательно, в данном случае, т. е. при шаровом заземлителе малого радиуса, поле растекания можно считать ограниченным объемом сферы радиусом примерно 20 м.

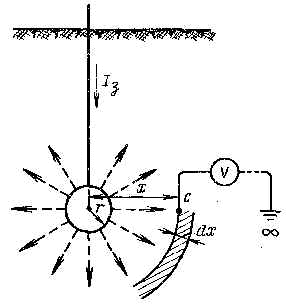
Рис. 3.1. Шаровой заземлитель, погруженный в землю на большую глубину

При постоянном токе, а также при переменном токе с частотой 50 Гц поле растекания тока в проводящей однородной среде можно рассматривать как стационарное электрическое поле, напряженность которого Е, В/м, связана с плотностью тока соотношением

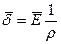
которое является законом Ома в дифференциальной форме.

При этом линии напряженности электрического поля совпадают с линиями плотности тока, которые в рассматриваемом случае совпадают также с радиусами шарового заземлителя. Как известно, напряженность электрического поля равна падению напряжения, отнесенного к единице длины линии напряженности поля. В данном случае

                                                          ,

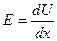где dU — падение напряжения, В, на участке dx, м, т. е. в элементарном слое земли толщиной dx (см. рис. 3.1).Пользуясь приведенными выражениями, легко определить потенциал любой точки в объеме земли, например точки С. Он равен падению напряжения в грунте на участке от x до бесконечности, т. е.

                                                            ,

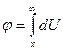где

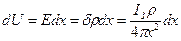
Решив этот интеграл, получим искомое уравнение для потенциала точки С, т. е. уравнение потенциальной кривой:

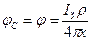                                              ,                          (3.1)

Потенциал j = 0, будет иметь точка, отстоящая от заземлителя на бесконечно большое расстояние х. Практически область нулевого потенциала начинается на расстоянии примерно 20 м от заземлителя. Потенциал точек на поверхности земли в данном случае равен нулю, поскольку, как мы условились, заземлитель находится от поверхности земли на бесконечно большом расстоянии.

Максимальный потенциал будет при наименьшем значении х, равном радиусу заземлителя r, т. е. непосредственно на заземлителе (потенциал шарового заземлителя на большой глубине):

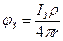                                   .                               (3.2)