машины

При рассмотрении начального момента внезапного изменения режима синхронную машину можно рассматривать как трансформатор [9]. Исследование начального момента произведем на основе принципа сохранения начального потокосцепления для выявления неизменной ЭДС и сопротивления при переходе от рабочего режима к режиму КЗ. Для машины без демпферных обмоток эти параметры носят название переходных. Рассмотрим изменение периодической составляющей для машины с параметрами, приведенными к статору в системе относительных единиц. Индексы комплексных величин опускаются.

 Рассмотрим картину магнитного поля синхронной машины.

Магнитный поток, сцепленный с ротором в момент внезапного изменения режима, остается неизменным. Кроме того, соответствующая ему ЭДС, наведенная в статоре, в тот же момент также остается неизменной. То есть для синхронной машины условия в начальный момент переходного процесса аналогичны тем же условиям для трансформатора, питаемого источником синусоидального напряжения.

Баланс магнитных потоков будет выглядеть следующим образом.

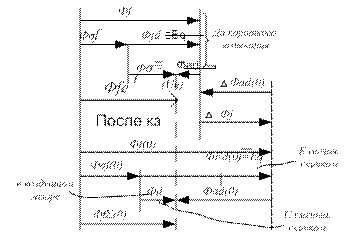
Рис. 6.2. Баланс магнитных потоков в синхронной машине

Из рисунка 6.2 видно, что при внезапном изменении режима остается неизменным результирующий магнитный поток, сцепленный с обмоткой возбуждения:

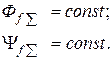                                          (6.1)

Часть этого потока, которая связана со статором, с учетом 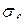 − коэффициента рассеивания обмотки возбуждения, т.е.  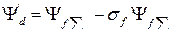наводит ЭДС в обмотке статора. Назовем эту ЭДС – переходной ЭДС 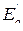. Она определяется:

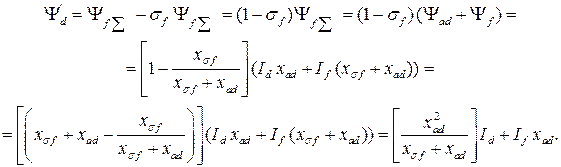(6.2)

Из (6.2) получаем следующее

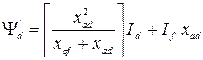.                           (6.3)

Умножим (6.3) на (- jω ). С учетом, что .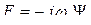                                       

Второе слагаемое в правой части уравнения (6.3) есть не что иное, как .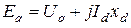

Тогда

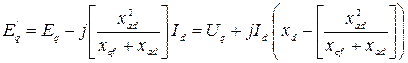.     (6.4)

Тогда переходная ЭДС из (6.4)

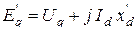.                                       (6.5)

До КЗ эту ЭДС можно измерить при условии, что 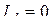. При этом получим 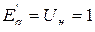, в остальных случаях она рассматривается как расчетная или фиктивная. Сверхпереходное сопротивление находится как

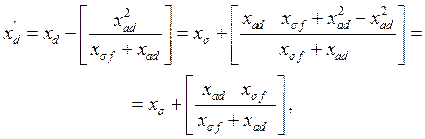           (6.6)

где .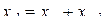

Из (6.6) видно, что 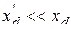, т.е. сопротивление при КЗ часто падает почти на порядок. Рассмотрим схему замещения.

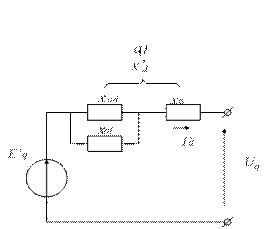
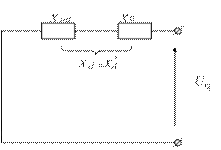
Рис. 6.3. Схемы замещения синхронной машины по осям в переходном режиме:

а) продольной; б) поперечной

Так как до и после КЗ переходная ЭДС одна и та же, это дает возможность определить  продольную составляющую тока КЗ − 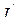. При отсутствии контуров по оси q 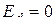, поэтому 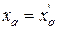, а, следовательно, после КЗ .

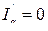Тогда полный ток КЗ будет равен:

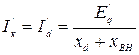.                                                (6.7)

Рис. 6.5. Векторная диаграмма

Здесь  

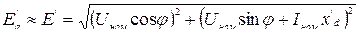.                       (6.8)

В (6.8) в скобках под знаком квадратного корня находятся фазные значения величин.