Для цепи, состоящей из последовательно соединенных элементов, определение постоянной времени не представляет труда, принимая в её расчете индуктивное и активное сопротивление всей короткозамкнутой цепи.

Решение сложной разветвленной сети наиболее эффективно достигается путем применения преобразований Лапласа, т.е. с использованием операторного метода. При этом число свободных составляющих равно числу ветвей сложной схемы. Для практических расчетов используют более простое приближенное решение. При этом эквивалентная постоянная времени

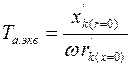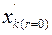, где и 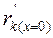 – суммарные сопротивления между источником питания и точкой КЗ, рассчитанные в предположении, что каждый элемент вводится в схему замещения своим либо активным, либо реактивным сопротивлением.

Полное сопротивление цепи КЗ при таком определении его составляющих не может быть использовано в расчетах, так как 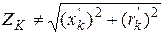. Такой  искусственный прием значительно упрощает решение и принят в стандарте на выключатели.

3.5. Действующие значения величин и их составляющих
  при переходном процессе

Понятие действующих значений величин необходимо для оценки действия электромагнитных переходных процессов, в том числе оценки теплового действия переменного тока в проводниках, а также именно действующие значения показывают электроизмерительные приборы.

Понятие действующего значения тока определяется из условия равенства теплового эффекта переменного и постоянного токов.

Пусть через некоторый участок электрической цепи с сопротивлением r протекает переменный ток i. Тогда по закону Джоуля−Ленца на этом участке за время T, соответствующее периоду тока i, будет выделено количество тепла, равное

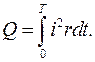                                     (3.17)

Обозначим через I некоторый постоянный ток, при протекании которого по тому же участку цепи за время T выделится такое же количество тепла. Тогда:

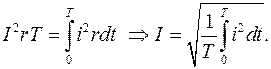                             (3.18)

При синусоидальном токе получим:   

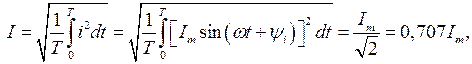           (3.19)

т.е. величина постоянного тока, эквивалентного переменному току по количеству выделяемого тепла, называется действующим или среднеквадратичным значением переменного тока. Как следует из выражения (3.19), действующее и амплитудное значения синусоидального тока связаны между собой постоянным коэффициентом.

По аналогии с током действующие значения вводятся для напряжений и ЭДС

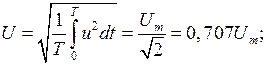
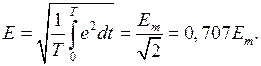(3.20)

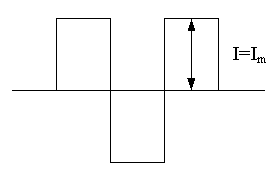
Рис. 3.9. Действующее значение тока прямоугольной формы

Действующее значение всегда меньше амплитудного значения переменной, в частном случае, при меандре (рис. 3.9), они могут быть равны .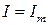

Действующее значение периодической и квазипериодической переменной можно найти двумя способами: разложением в ряд Фурье и численным вычислением интеграла.

1. Разложение в ряд Фурье. При наличии аналитического выражения функции i(t) и возможности взятия интеграла действующее значение тока определяется точно. Однако в общем случае на практике действующее значение определяется на основе информации о действующих значениях конечного ряда гармонических составляющих.

Пусть 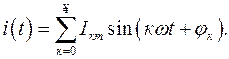 Тогда

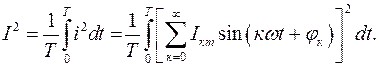
Таким образом, 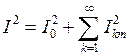 или 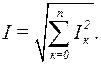                             (3.21)

Аналогичные выражения имеют место для ЭДС, напряжения и т.д. т.е. они определяются знакомым из курса электротехники выражением для действующего значения несинусоидальных величин [13].

2. Численное вычисление интеграла.

Так как функция i² является непрерывной во всем интервале [0,Т], то интеграл   (3.18 ) можно вычислить методом численного интегрирования с заменой интеграла на конечную сумму. Вычисление проводится путем разбиения интервала от 0 до Т на множество конечных интервалов, приближенным нахождением площади каждой полоски, получающейся при таком разбиении, и дальнейшем суммировании площадей этих полосок. Следовательно, действующее значение тока в этом случае находится по формуле: 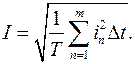                                 (3.22)

Таким образом, можно найти, например, действующее значение квазипериодической функции тока намагничивания  при включении трансформатора на холостом ходу (рис. 3.10).

Так как действующее значение переменного тока – это величина постоянного тока эквивалентного переменному току по количеству выделяемого тепла, то действующее значение переменного тока можно охарактеризовать интегралом Джоуля (тепловым импульсом).

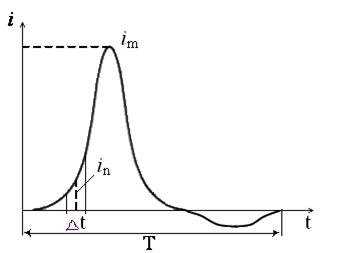
Рис. 3.10.  К численному вычислению интеграла

Количественную оценку степени термического воздействия тока КЗ на про­водники и электрические аппараты рекомендуется производить с помощью интегра­ла Джоуля

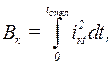                              (3.23)

где 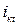 − ток КЗ в произвольный момент времени t, A;

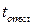− расчетная продолжительность КЗ, с.

Интеграл Джоуля допускается определять приближенно как сумму интегра­лов от периодической и апериодической составляющих тока КЗ, т.е.

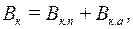                             (3.24)

где 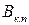− интеграл Джоуля от периодической составляющей тока КЗ;

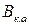− интеграл Джоуля от апериодической составляющей тока КЗ.

В случае, когда 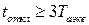 интеграл Джоуля также допустимо определять по формуле:

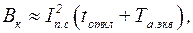                        (3.25)

где 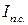− действующее значение периодической составляющей тока КЗ от источника (системы), А;

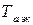 − эквивалентная постоянная времени затухания апериодической составляющей тока КЗ, с.                       

Расчетную продолжительность КЗ при проверке проводников и электрических аппаратов на термическую стойкость при КЗ следует определять сложением времени действия основной релейной защиты, в зону действия которой входят проверяемые проводники и аппараты, и полного времени отключения ближайшего к месту КЗ выключателя, а при проверке кабелей на невозгораемость − сложением времени действия резервной релейной защиты и полного времени отключения соответствующего выключателя.

При расчетной продолжительности КЗ до 1 с процесс нагрева проводников под действием тока КЗ допустимо считать адиабатическим, а при расчетной продолжительности более 1 с и при небыстродействующих АПВ следует учитывать теплоотдачу в окружающую среду.                       

В тех случаях, когда нагрузка проводника до КЗ близка к продолжительно допустимой, минимальное сечение проводника, отвечающее условию термической стойкости при КЗ, следует определять по формуле:

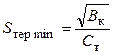,                                             (3.26)

Значения параметра С_т для жестких шин и кабелей принимаются по справочным данным [2].

Проверка выключателя на термическую стойкость при КЗ заклю­чается в сравнении найденного при расчетных условиях значения интеграла Джоуля В_к с его допустимым для проверяемого выключателя значением В_к.доп . Выключатель удовлетворяет условию термической стойкости, если выполняется условие

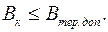                                 (3.27)

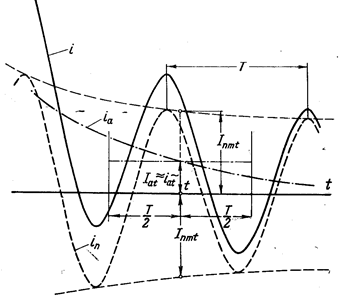
Рис. 3.11. Составляющие и полный ток КЗ

При упрощенные расчетах переходных процессов и наличии только периодической 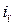 и апериодической  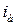составляющих тока (рис. 3.11), которые определены по их значениям в середине рассматриваемого периода действующее значение  периодической составляющей

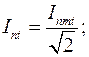                                       (3.28)

действующее значение апериодической составляющей за один период равно мгновенному значению в момент, находящийся посредине данного периода

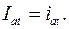                           (3.29)

Действующее значение полного тока в тот же момент будет равно:

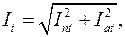                               (3.30)

Наибольшее действующее значение полного тока короткого замыкания 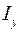 имеет место за первый период переходного процесса. При условии 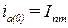, его можно определить как:

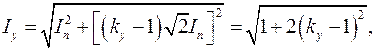             (3.31)

где k _у – ударный коэффициент, 1< k _у < 2.

Согласно этому, величина отношения 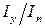 находится в пределах

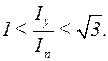                         (3.32)

Следовательно, в расчетах переходных процессов апериодическая составляющая должна учитываться.