Частотная и фазовая модуляции тесно связаны, потому что частота и фаза тесно связаны между собой. Это не так очевидно, если вы считаете, что частота равна числу полных циклов в секунду – как число циклов в секунду связано с положением синусоиды в заданный момент во времени цикла? Но это имеет смысл, если вы считаете мгновенную частоту, т.е. частоту сигнала в заданный момент (несомненно, парадоксально описывать частоту как мгновенную, но в контексте практической обработки сигналов мы можем смело игнорировать сложные теоретические детали, связанные с этой концепцией).
В базовой синусоиде значение мгновенной частоты совпадает со значением «нормальной» частоты. Аналитическое значение мгновенной частоты появляется, когда мы имеем дело с сигналами, у которых частота изменяется во времени, т.е. частота является не постоянным значением, а скорее функцией времени, записанной как ω(t). В любом случае, важным моментом нашего текущего обсуждения относительно тесной взаимосвязи между частотой и фазой является следующее: мгновенная угловая частота является производной фазы по времени. Поэтому, если у вас есть выражение φ(t), которое описывает изменяющееся во времени поведение фазы сигнала, то скорость изменения φ(t) (по времени), дает вам выражение для мгновенной угловой частоты.
закончим следующим графиком, который показывает математическую взаимосвязь в частотной модуляции между низкочастотным сигналом и сигналом несущей частоты, используемых ранее:
мы будем обозначать несущую как sin (ω нес*t). У нее уже есть частота (а именно, ω нес*t), поэтому мы должны использовать термин «дополнительное отклонение частоты» для обозначения частотной составляющей, внесенной процедурой модуляции. Этот термин несколько вводит в заблуждение, поскольку «дополнительное» подразумевает более высокую частоту, тогда как модуляция может приводить к несущей частоте, которая выше или ниже номинальной несущей частоты. Фактически поэтому частотная модуляция (в отличие от амплитудной модуляции) не требует смещенного низкочастотного сигнала: положительные значения низкочастотного сигнала увеличивают частоту несущей, а отрицательные значения низкочастотного сигнала уменьшают частоту несущей. В этих условиях демодуляция не является проблемой, поскольку все значения низкочастотного сигнала соответствуют уникальным частотам.
В любом случае, вернемся к нашему сигналу несущей: sin (ω несt). Если мы добавим низкочастотный сигнал (xнч) к величине внутри круглых скобок, мы получим отклонение фазы, линейно пропорциональное низкочастотному сигналу. Но нам нужна частотная модуляция, а не фазовая, поэтому мы хотим, чтобы линейно пропорционально низкочастотному сигналу было отклонение частоты. Из первой статьи данной главы мы знаем, что мы можем получить частоту, взяв производную фазы по времени. Таким образом, если мы хотим, чтобы частота была пропорциональна xнч, мы должны добавить не сам низкочастотный сигнал, а скорее интеграл от низкочастотного сигнала (поскольку взятие производной отменяет интеграл, у нас остается xнч как отклонение частоты).
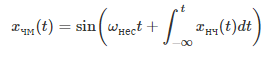
нужно здесь добавить, это индекс модуляции m. В предыдущей статье мы увидели, что индекс модуляции можно использовать для того, чтобы изменения амплитуды несущей были более или менее чувствительны к изменениям амплитуды низкочастотного сигнала. Его функция в FM аналогична: индекс модуляции позволяет нам точно настраивать интенсивность изменения частоты, которое возникает при изменении амплитуды низкочастотного сигнала.
несущая 10 МГц:
Низкочастотным модулирующим сигналом будет синусоида 1 МГц, показанная ниже:
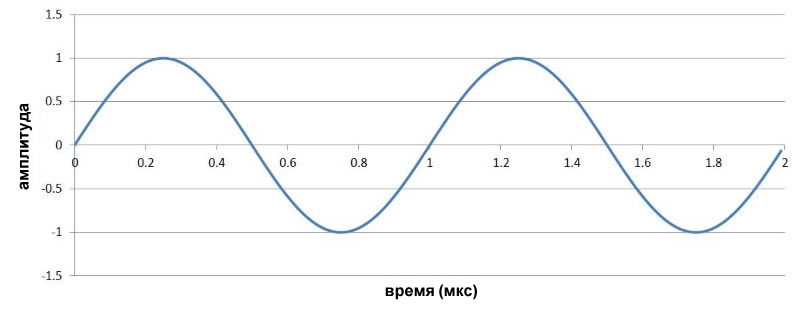
Низкочастотный сигнал
Частотно-модулированный сигнал генерируется с помощью формулы, приведенной выше. Интеграл от sin(x) равен -cos(x) + C. Константа C здесь не важна, поэтому для вычисления FM сигнала мы можем использовать следующую формулу:
Результат показан ниже (красным показан низкочастотный модулирующий сигнал):
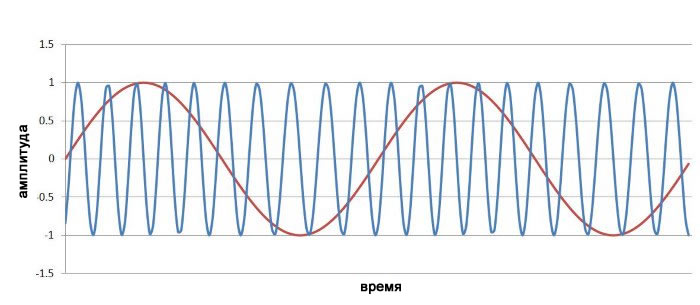
Частотная модуляция
Частотная область
Формы AM и FM сигналов, при одинаковых сигнале несущей и низкочастотном модулирующем сигнале выглядят совершенно по-разному. Поэтому интересно обнаружить, что AM и узкополосная FM дают аналогичные изменения в частотной области. (Узкополосная частотная модуляция предусматривает ограниченную полосу модулирующего сигнала и позволяет упростить анализ.) В обоих случая низкочастотный спектр (включая отрицательные частоты) переносится в полосу, которая простирается выше и ниже несущей частоты. В AM спектр самого низкочастотного модулирующего сигнала сдвигается вверх. В FM это спектр интеграла низкочастотного модулирующего сигнала, который появляется в полосе, окружающей несущую частоту.
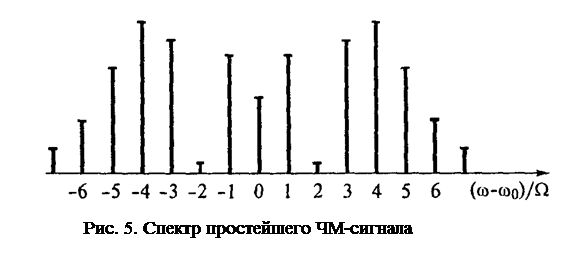
Для модуляции, показанной выше, с m=1 мы получаем следующий спектр:
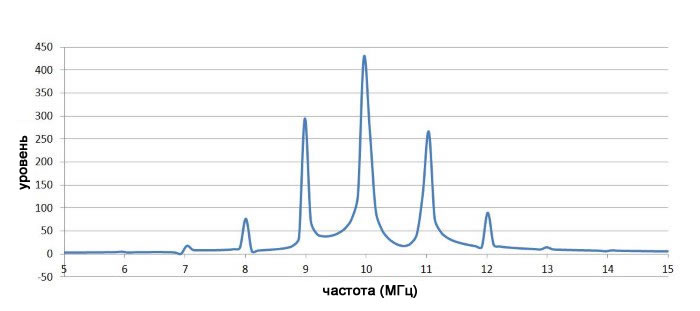
Следующий спектр соответствует m=4:
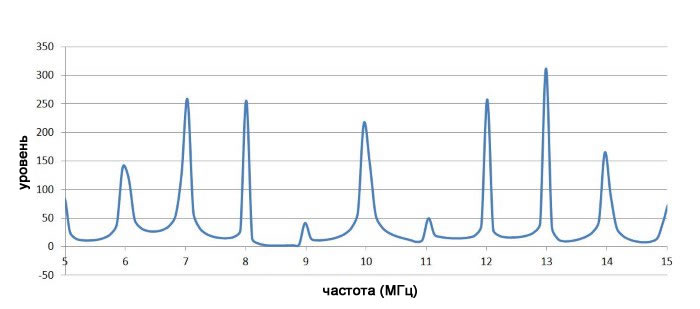
Спектр частотно-модулированного сигнала при m=4
индекс модуляции влияет на частотные составляющие частотно-модулированного сигнала. Спектральный анализ частотной модуляции сложнее, чем для амплитудной модуляции; поэтому для частотно-модулированных сигналов трудно предсказать ширину полосы частот.
Вывод
- Математическое представление частотной модуляции состоит из синусоидального выражения с интегралом низкочастотного модулирующего сигнала, добавленного к аргументу функции синуса или косинуса.
- Индекс модуляции может использоваться, чтобы сделать отклонение частоты более чувствительным или менее чувствительным к изменениям амплитуды низкочастотного модулирующего сигнала.
- Узкополосная частотная модуляция приводит к переносу спектра интеграла низкочастотного модулирующего сигнала в полосу, окружающую несущую частоту.
- На спектр ЧМ влияет индекс модуляции, а также отношение амплитуды модулирующего сигнала к частоте модулирующего сигнала.
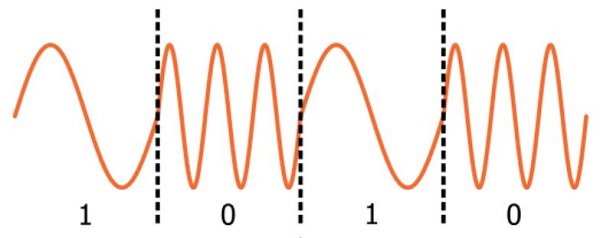
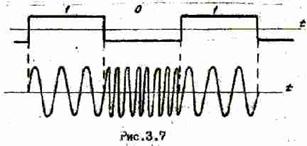
· При частотной модуляции (ЧМ) изменяется частота гармонического сигнала соответственно значащей позиции сигнала данных. Единичные элементы, соответствующие символам данных 1 и 0, представляются в виде (рис.3.7):
· 
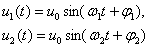
· где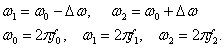 
· Разность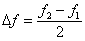 
называют девиацией частоты, отношение 
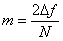-индексом модуляции, а 
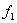и 
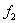- характеристическими частотами. Спектр ЧМ сигнала занимает значительно большую полосу частот, чем при ДМ (естественно при одинаковой скорости передачи).
· 
· За счет ограничения спектра возникает переходный процесс как по амплитуде, так и по частоте. Длительность установления частоты от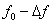 
до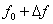 
зависит от отношения 
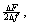где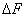 
- необходимая полоса частот, устанавливаемая для передачи двоичного ЧМ сигнала. Компромисс между допустимыми искажениями и необходимой полосой частот достигается при значениях 
.
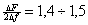· Таким образом, необходимая полоса частот 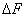для передачи двоичного ЧМ сигнала с допустимыми искажениями определяется выражением
· 
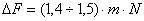
· Удельная скорость передачи при m>1 близка к значение 0,5 бит/с*Гц
· становлено, что при m <1 основная энергия сигнала сосредоточена вблизи несущей частоты 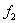, поэтому можно достичь удельной скорости передачи 1бит/с*Гц. Например, при
· 
· 
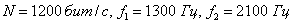
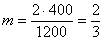
· Тогда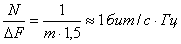 
· Для формирования ЧМ сигнала используются управляемый генератор (УГ), частота которого может изменяться без скачков фазы и со скачками фазы. Реализация ЧМ без разрыва фазы осуществляется непосредственным воздействием первичного сигнала А(t) на частоту генератора несущего колебания. ЧМ с разрывом фазы получается использованием независимых генераторов, настроенных на требуемые частоты, и спектр амплитуд модулированного сигнала занимает более широкую полосу частот, чем при формировании без разрыва фазы.
· Демодуляция ЧМ сигналов может осуществляться когерентным и некогерентным методом. Последний широко используется при передаче данных с низкой удельной скоростью. Общим принципом демодуляции является частотное детектирование (ЧД) с помощью дискриминаторов, которые преобразуют изменение частоты в изменение амплитуды.
· Так как изменяемым параметром сигнала является частота, то для уменьшения влияния помех применяют ограничители амплитуд Огр, что существенно повышает помехозащищенность ЧМ по сравнению с АМ. На рис.3.8 представлена структурная схема модема с ЧМ.
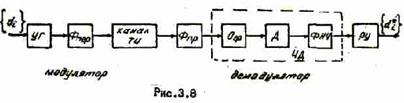
Сигнал данных управляет частотой генератора УГ несущего колебания. Подавление побочных продуктов модуляции на передаче и помех на приеме производят соответственно фильтры передачи Ф пер и приема Ф пр. Ограничитель Огр снижает амплитудные искажения. Дискриминатор Д преобразует изменения частоты сигнала в изменение амплитуды. Фильтр нижних частот ФНЧ подавляет составляющие преобразованного сигнала частотами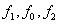 
и др. Решение о принимаемом сигнале принимается решающим устройством РУ.
Модемы с ЧМ благодаря несложной технической реализации и сравнительно высокой помехозащищенности рекомендованы МККТТ для передачи данных по стандартным каналам ТЧ со скоростью до 1200 бит/с.
Частотной модуляции присущ недостаток - высокая чувствительность к изменению частоты сигнала при передаче по каналу ТЧ
Тая как в дискриминаторе происходит преобразование ЧМ сигнала в AM сигнал, то при неизменном пороге регистрации сдвиг по частоте переходит в сдвиг по длительности, т.е. появляются так называемые искажения типа преобладания «когда длительность посылок одной полярности превосходит длительность посылок другой полярности. На рис.3.9 показана пунктиром передача двухполюсной последовательности сигналов данных ("точек") по каналу без изменения частоты сигнала, и сплошной линией - по каналу с изменением частоты сигнала на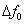 
. На рисунке 
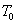-длительность единичного элемента сигнала данных 
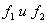характеристические частоты.
Для устранения подобного рода искажений в процессе настройки дискретного канала с ЧМ всегда производится регулировка на нейтральность.
)
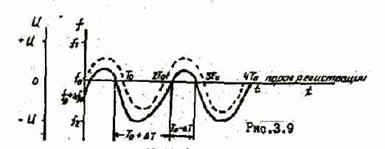
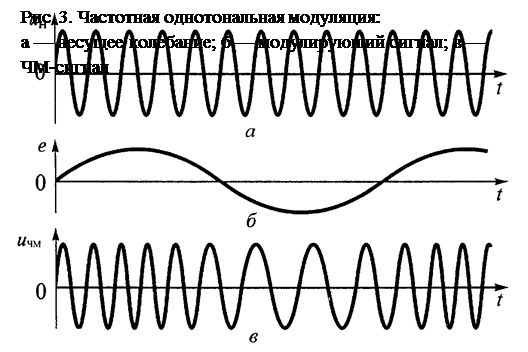
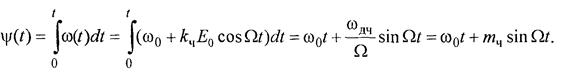
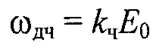
- максимальное отклонение частоты от значения ω0, или девиация частоты (frequency deviation) при частотной модуляции;
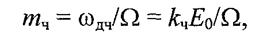— максимальное отклонение от текущей фазы ω0t или девиация фазы несущего колебания называется индексом частотной модуляции (index of frequency modulation). Данный параметр определяет интенсивность колебаний начальной фазы радиосигнала.
С учетом полученных соотношений (1) и (16) частотно-модулированный сигнал запишется в следующем виде:
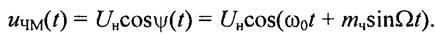
Спектр ЧМ-сигнала при однотональной модуляции. Преобразуем полученное выражение (17)
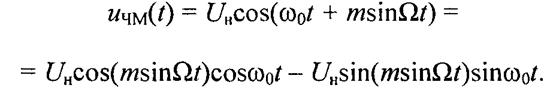
Спектр ЧМ-сигнала при m«1 (такую угловую модуляцию называют узкополосной). В этом случае имеют место приближенные равенства: (18)
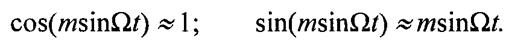
Подставив формулы (18) в выражение (17), после несложных математических преобразований получим (при начальных фазах модулирующего и несущего колебаний θ0 = 0 и φ0 = 0): (19)
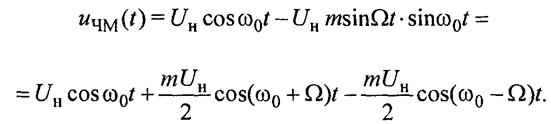
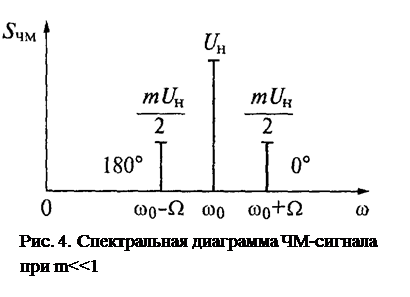
Видим, что по аналитической записи спектр ЧМ-сигнала при однотональной модуляции напоминает спектр АМ- сигнала и также состоит из несущего колебания и двух боковых составляющих с частотами (ω0+ Ω) и (ω0- Ω) причем и амплитуды их рассчитываются аналогично (только вместо коэффициента амплитудной модуляции М в формуле для ЧМ-сигнала фигурирует индекс угловой модуляции m). Но есть и принципиальное отличие, превращающее амплитудную модуляцию в частотную, знак минус перед одной из боковых составляющих.
|
|
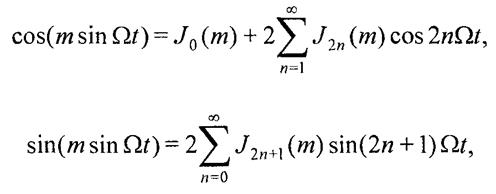
Спектр ЧМ-сигнала при m> 1. Из математики известно (20) (21)
где Jn(m) — функция Бесселя 1 -го рода n-го порядка.
В теории функций Бесселя доказывается, что функции с положительными и отрицательными индексами связаны между собой формулой (22)
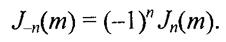
Ряды (20) и (21) подставим в формулу (17), а затем заменим произведение косинусов и синусов полусуммами косинусов соответствующих аргументов. Тогда, с учетом (22), получим следующее выражение для ЧМ-сигнала (23)
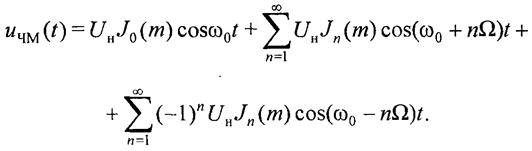
Итак, спектр ЧМ-сигнала с однотональной модуляцией при индексе
модуляции m > 1 состоит из множества высокочастотных гармоник: несущего колебания и бесконечного числа боковых составляющих с частотами ω0+ nΩ. и ω0-nΩ, расположенными попарно и симметрично относительно несущей частоты ω0.
При этом, исходя из (22), можно отметить, что начальные фазы боковых колебаний с частотами ω0+ nΩ. и ω0-nΩ совпадают, если m — четное число, и отличаются на 180°, если m — нечетное. Теоретически спектр ЧМ- сигнала (так же и ФМ-сигнала) бесконечен, однако в реальных случаях он ограничен. Практическая ширина спектра сигналов с угловой модуляцией
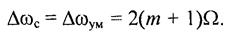
ЧМ- и ФМ-сигналы, применяемые на практике в радиотехнике и связи, имеют индекс модуляции m>> 1, поэтому
|
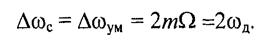
Полоса частот ЧМ-сигнала с однотональной модуляцией равна удвоенной девиации частоты и не зависит от частоты модуляции.
Сравнение помехоустойчивости радиосистем с амплитудной и угловой модуляцией. Следует отметить, что радиосигналы с угловой модуляцией имеют ряд важных преимуществ перед амплитудно-модулированными колебаниями.
1. Поскольку при угловой модуляции амплитуда модулированных колебаний не несет в себе никакой информации и не требуется ее постоянства (в отличие от амплитудной модуляции), то практически любые вредные нелинейные изменения амплитуды радиосигнала в процессе осуществления связи не приводят к заметному искажению передаваемого сообщения.
2. Постоянство амплитуды радиосигнала при угловой модуляции позволяет полностью использовать энергетические возможности генератора несущей частоты, который работает при неизменной средней мощности колебаний.
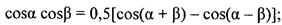
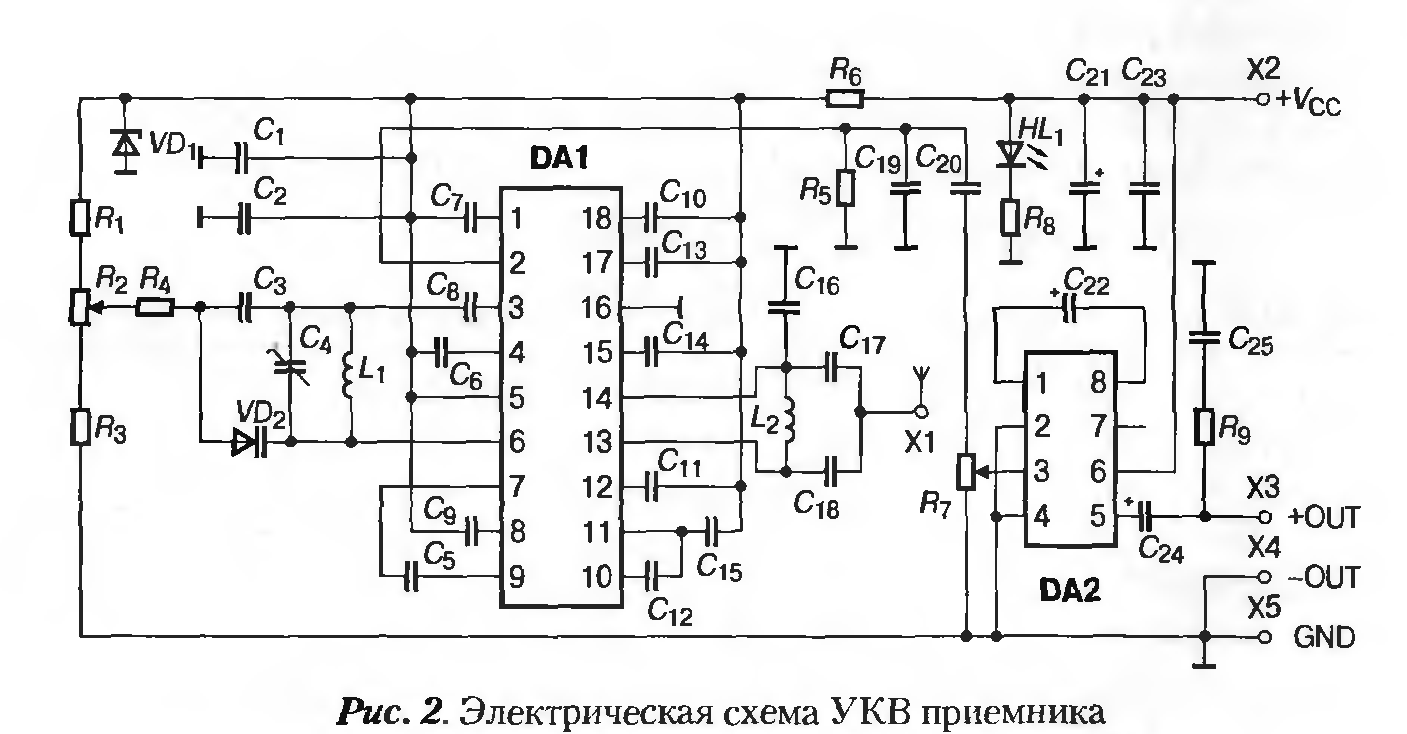
Описание работы УКВ приемника
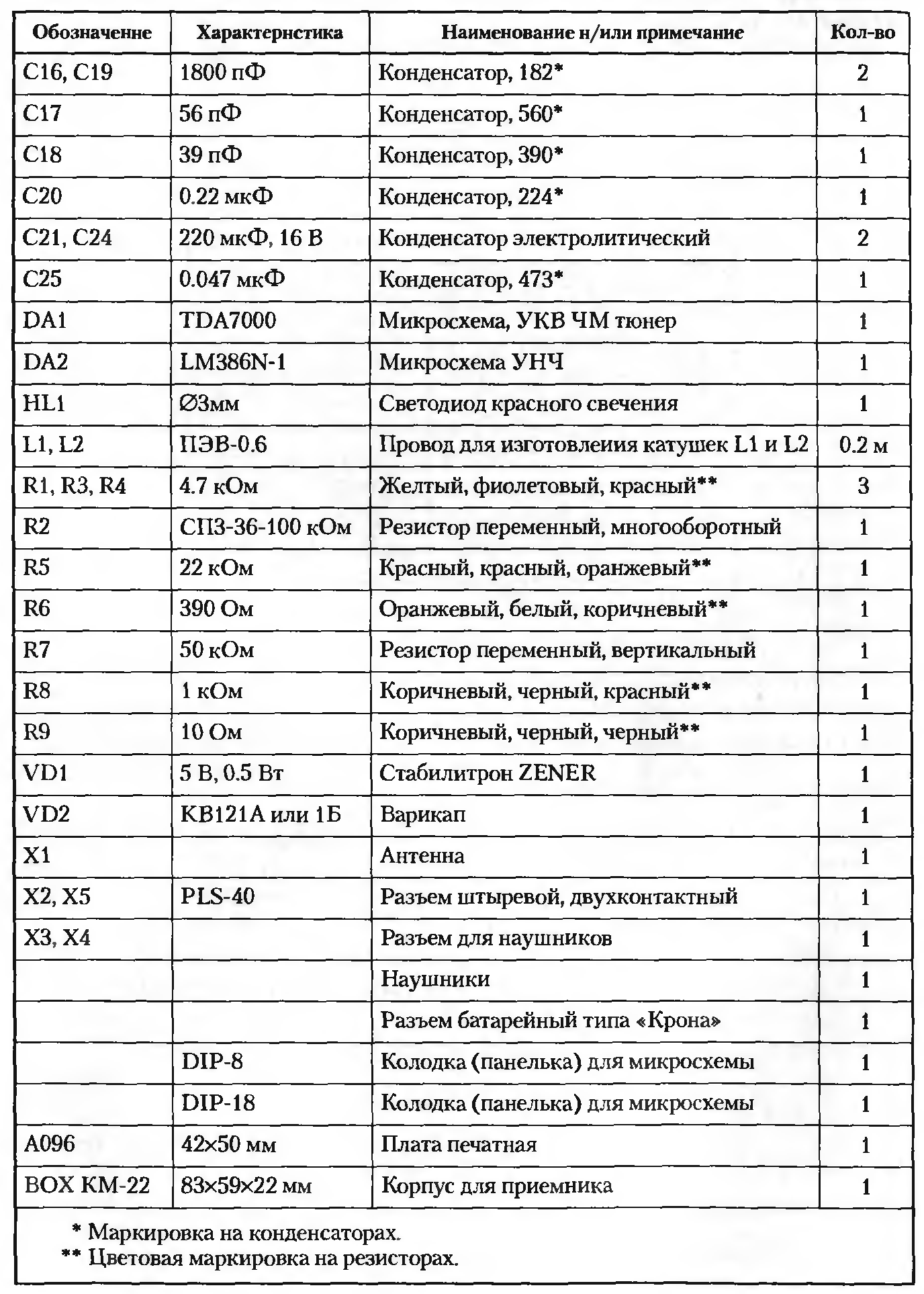
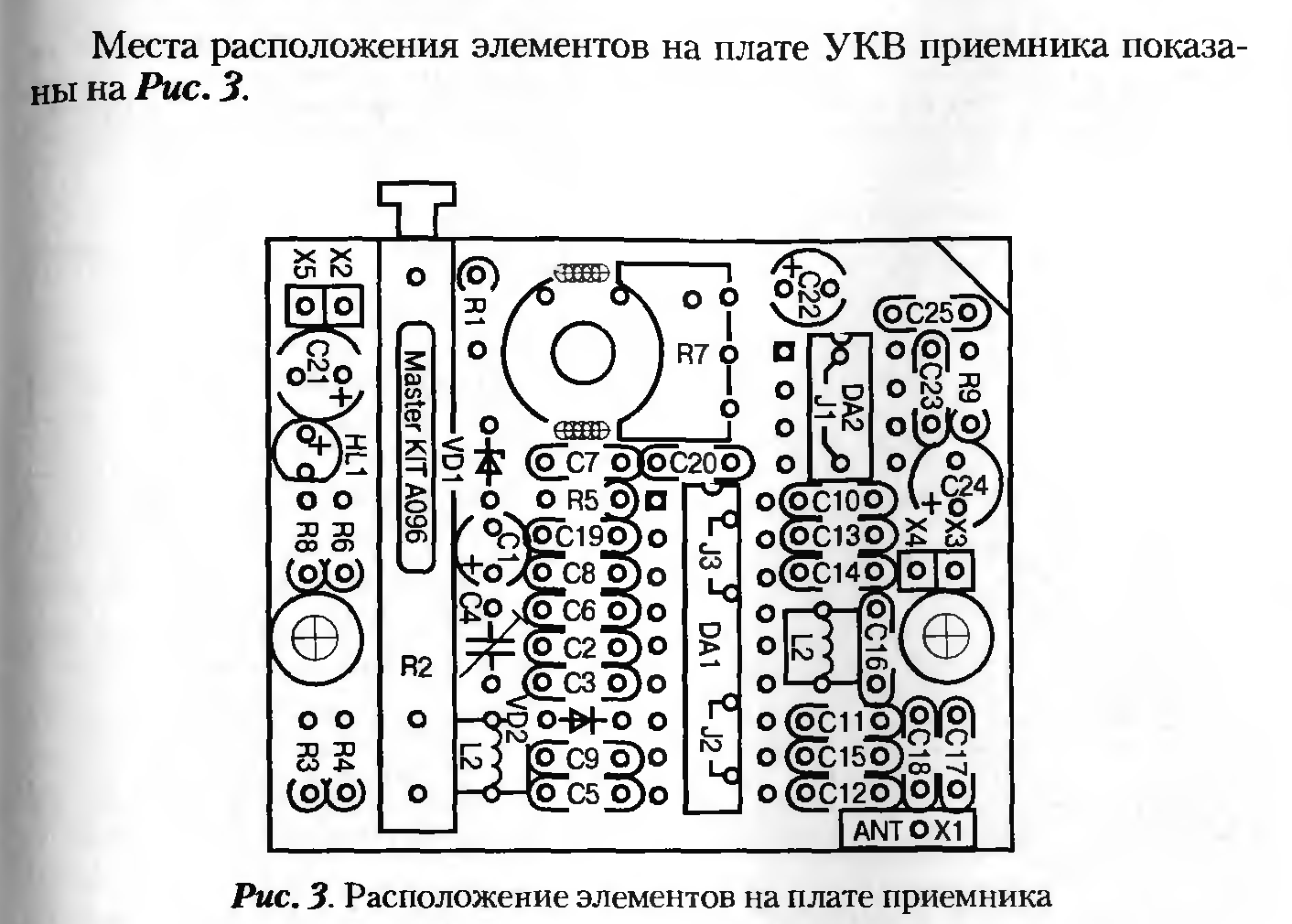
Самое простое радио
Схема приемника показана на рис. 1. Эта схема очень близка к схеме приемника,. Только УКВ резонансный контур был добавлен в цепь.
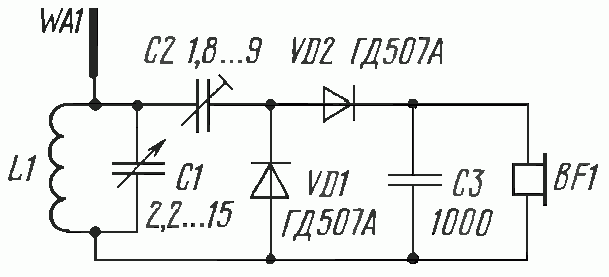
рис. 1.
ВД1, VD2 - GD507A - старый СССР германиевые высокочастотные диоды с емкостью 0.8 ПФ (при обратном напряжении 5В), время восстановления обратного сопротивления не более 0,1 с нами (у меня прямые импульса=10 мА, U иобратного импульса=20 в, Iотсечки=1 ма
Устройство содержит телескопическую антенну WA1, непосредственно соединенную с резонансным баком L1C1. Антенна также является элементом резонансного резервуара, поэтому для получения максимальной мощности сигнала необходимо регулировать как длину антенны, так и частоту цепи резервуара. В некоторых случаях, особенно когда длина антенны составляет около 1/4 длины волны, полезно подключить антенну к крану катушки настройки L1 (найти подходящий кран катушки, находя Максимальный объем сигнала).
Соединение с детектором может быть регулирует триммером C2. На самом деле детектор состоит из двух высокочастотных германиевых диодов VD1 и VD2. Цепь совершенно идентична к цепи выпрямителя тока напряжения тока удваивая, но обнаруженное напряжение тока было бы удвоено если только значение конденсатора К2 триммера высоко, то но после этого нагрузка резонирующей цепи Л1К1 была бы чрезмерна, и свой фактор качества к будет низок. В результате, напряжение тока сигнала в баке l1c1 цепи будет более низко и тонально звуковой том будет более низок слишком.
В нашем случае емкость соединительного конденсатора С2 достаточно мала и удвоения напряжения не происходит. Для оптимального согласования схемы детектора с цепью резервуара сопротивление конденсатора связи должно быть равно геометрическому среднему между входным сопротивлением детектора и резонансным сопротивлением цепи резервуара L1C1. При таком условии детектор получает максимальную мощность высокочастотного сигнала, что соответствует максимальной громкости звука.
Конденсатор С3 шунтирует более высокие частоты на выходе детектора. Нагрузка на детектор-наушники с сопротивлением постоянного тока не менее 4K ом. Весь блок собран в малом снабжении жилищем металла или пластмассы. К верхней части корпуса крепится телескопическая антенна длиной не менее 1 м, а к разъему или гнезду для телефонов крепится нижняя часть корпуса. Обратите внимание, что телефонный шнур является второй половиной дипольной антенны (противовеса).
Катушка L1 бескаркасная, содержит 5 витков эмалированной медной проволоки диаметром 0,6...1 мм намотано на оправку диаметром 7 мм...8 мм. Вы можете отрегулировать необходимую индуктивность путем протягивать или обжимать повороты катушки L1. Лучше использовать переменный конденсатор С1 с воздушным диэлектриком, например, типа 1КПВМ с двумя или тремя подвижными и одной или двумя неподвижными пластинами. Своя максимальная емкость мала и может находиться в границах 7...15 p. Если переменный конденсатор имеет больше пластин (емкость выше), желательно удалить любую из пластин или подключить переменный конденсатор последовательно с постоянным конденсатором или триммером, это уменьшит максимальную емкость.
Конденсатор К2 керамический конденсатор триммера, как КПК или КПК-м с емкостью 2...7 pF. Другие конденсаторы триммеров смогли быть использованы слишком. Подстроечный конденсатор C2 может быть заменен на переменный конденсатор, похожий на C1, и его можно использовать для регулировки сцепления "на лету" для оптимизации возможностей приема радио.
Диоды VD1 и VD2, могут быть GD507B, D18, D20 (это старые Германиевые высокочастотные диоды СССР. Эти диоды можно заменить на современные диоды Шоттки). Шунтируя конденсатор C3 керамический, своя емкость не критическая и может иметь значение в ряде от 100 до 4700 pF.
Регулировка приемника проста. Настройте радио путем поворачивать ручку на переменном конденсаторе C1 и отрегулируйте конденсатор C2 для того чтобы получить максимальный тонально звуковой том. Настройка резонансного бака L1C1 будет изменена, поэтому все операции необходимо повторить еще несколько раз, и при этом найти лучшее место для приема радио. Это не обязательно то же место, где электрическое поле имеет максимальную силу. Это должно быть обсуждено более подробно и объяснить, почему этот приемник может принимать FM-сигналы.
Интерференция и преобразование FM в AM
Если танк схема фильтр l1c1 нашего приемника (рис. 1) будет настроить так, чтобы несущая частота ЧМ сигнала падает на склоне резонансной кривой, FM может быть преобразован в АМ. Найдем значение Q контура танка. При условии, что полоса пропускания цепи бака фильтр l1c1 равна удвоенной девиации частоты, получим г = ф0 /Δ2f = 700 за оба верхний и Нижний УКВ.
Фактический Q цепи бака в кристаллическом радио вероятно будет чем 700 из-за низкого Q-фактора своего Q (около 150...200) и потому что резонирующий бак шунтирован антенной и входным сопротивлением детектора. Тем не менее, слабое преобразование FM в AM возможно, таким образом, приемник будет едва работать, если его цепь сместить немного вверх или вниз по частоте.
Однако есть гораздо более мощный фактор, способствующий превращению FM в АМ, - это интерференция. Это очень редко, когда приемник находится в поле зрения радиостанции, в большинстве случаев линия визирования скрыта зданиями, холмами, деревьями и другими светоотражающими объектами. К антенне приемника поступает несколько радиосигналов, рассеянных этими предметами. Даже на линии визирования к антенне поступает несколько отраженных сигналов (и, конечно же, поступает и прямой сигнал). Общий сигнал зависит как от амплитуд, так и от фаз составляющих суммирования.
Два сигнала суммируются, если они находятся в фазе, т. е. разность их путей кратна целому числу длины волны, и два сигнала вычитаются, если они находятся в противоположной фазе, когда разность их путей одинаковое количество длин волн плюс половина длины волны. Но длина волны, как и частота, изменяется при FM! Разница Пучков и их относительный сдвиг фаз будут меняться. Если разница в способах велика, то даже небольшое изменение частоты приводит к значительным сдвигам в фазах. Элементарный геометрический расчет приводит к формуле: равна δf/ф0 = λ/4ΔC, или ΔC = ф0/λ/4Δf, где ΔC - разность путей , это необходимо для сдвига фаз ±Π/2, чтобы получить полную сумму АМ-сигнала, равна δf - девиация частоты. Полный АМ-это полное изменение амплитудного сигнала от суммы амплитуд двух сигналов к их разности. Формулу можно еще более упростить, если учесть, что произведение частоты на длину волны ф0λ равна скорости света c: ΔC = с/4Δf.
Теперь легко рассчитать, что для получения полного АМ ДВУХЛУЧЕВОГО FM сигнала, достаточная разница между путями лучей составляет около километра. Если разница путей меньше, то глубина АМ пропорционально уменьшается. Ну, но если разница в способах больше? Затем в течение одного периода модулирующего аудиосигнала общая амплитуда интерферирующего сигнала будет проходить несколько раз через максимумы и минимумы, а искажения будут очень сильными при преобразовании FM в AM, вплоть до полного нечеткого звука при получении FM с помощью am-детектора.
Помехи при приеме FM-вещания-крайне вредное явление. Он не только производит сопутствующий паразитический АМ сигнала, как это описано выше, но и производит паразитную фазовую модуляцию, что приводит к искажению, даже если мы получили хороший приемник FM. Поэтому так важно разместить антенну в нужном месте, где преобладает только один сигнал. Всегда лучше использовать направленную антенну, так как она увеличивает величину прямого сигнала и уменьшает отражения, поступающие из других направлений.
Только в этом случае при очень простом детекторном радиоприемнике интерференция играла полезную роль и позволяла слушать радиопередачу, но радиопередачу можно услышать слабо или со значительными искажениями, а радиопередачу можно услышать не везде, а только в определенных местах. Этим объясняются периодические изменения в объеме радиопередачи в Терлецком парке.
Дата: 2019-02-02, просмотров: 916.
