<

Экспериментальные данные характеризующие вариационный ряд

;	;	;

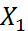
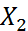
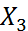
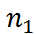
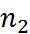
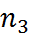
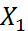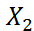
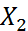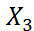
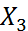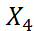
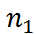
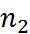
При этом считается, что промежуток содержит свой конец, а самый последний промежуток содержит правый конец.

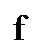
Нарисуйте график плотности стандартного нормального распределения, указав на нём величины среднего значения и стандартного отклонения. В чём его «удобство» по сравнению с «обычным» нормальным распределением? Какие ещё распределения случайных величин Вы знаете?

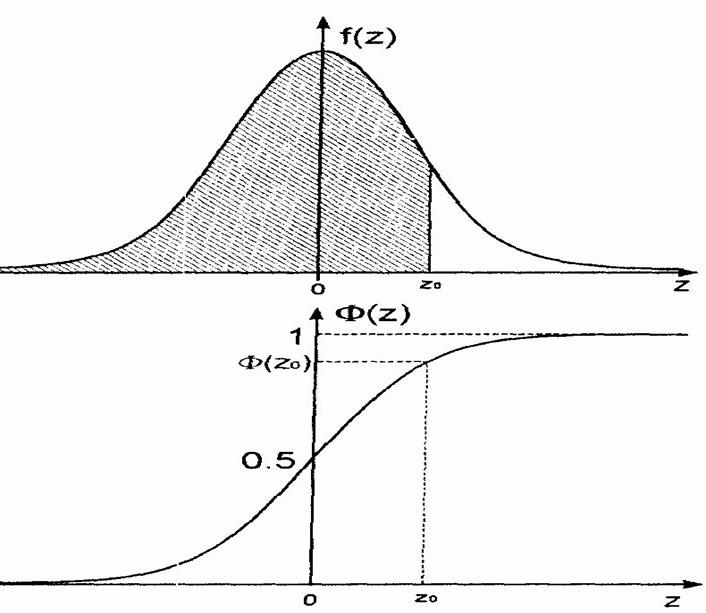
Графики плотности и интегральной функции "стандартного нормального распределения".

«Стандартное нормальное распределение» отличается от других распределений этого типа тем, что в нём µ = 0 и σ=1.

Основные дискретные распределения:

· Биномиальное (р = 0,95, биномиальное распределение симметрично при р = 0,5. При р ≠ 0,5 распределение приближается к симметричному при уве­личении n; приближение будет происходить тем быстрее, чем ближе значение р к 0,5, Кроме того, при увеличении n биноми­альное распределение можно аппроксимировать нормальным распределением с теми же математическим ожиданием и дис­персией) - выражает вероятность успеха при проведении повторных испытаний

· Распределение Пуассона (р → 0, n → ∞.)– когда число опытов n достаточно велико, а вероятность р - достаточно мала, т.е. в каждом отдельном опыте интересующее событие происходит крайне редко. Отсюда происходит применяющееся иногда для закона Пуассона название «закон редких явлений».

· Гипергеометрическое распределение (представим, что проверяется партия N изделий готовой продукции, содер­жащая М годных и N - М негодных изделий. Случайным обра­зом выбирают n изделий. Число годных изделий k , среди вы­бранных, описывается гипергеометрическим распределением) – выражает число отказов изделий соотв. качества в выборке.

7. Назовите основные точечные оценки положения рассеяния случайных величин на числовой оси и приведите известные Вам формулы их определения: аналитические и используемые в рамках программы MS Excel.

Точечные оценки положения, степени и характера рассеяния случайной величины на числовой оси:

Выборочное среднее (среднее арифметическое, математическое ожидание) случайной величины 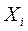обозначается как  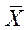удовлетворяет всем приведённым выше требованиям к точечным оценкам.

Медиана (Me) x_1/2, квартили х_1/4, х_1/2, х_3/4, децили х₀₁...х₀₉(или х_0,1...х_0,9) и процентили х₀₀₁...х₀₉₉(или х_0,01...х_0,99) делят упорядоченное распределение (вариационный ряд) Х соответственно на 2,4,10 или 100 интервалов, рис. 3.2.

Мода (Мо)случайной величины - наиболее вероятное значение случайной величины. Иначе - это значение случайной величины, при котором плотность распределения вероятностей имеет максимум.

Показатели степени разброса(кучности):

- среднеарифметическое отклонение (центральный момент первого порядка) ρ (ро)

- дисперсия (D)

- стандартное отклонение (ско, σ, 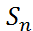) σ=1,25ρ; S≈1,25 ≯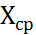

- размах (R)

- межквартильный размах ( - )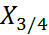

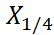Показатели асимметрии разброса:

- коэффициент асимметрии А (центр момент 3-го порядка)

- положение медианы и моды относительно среднего и относительно квартилей

Показатели характеризующие закон распределения:

- вариационный ряд

- гистограмма

- полигон частот

- график интегральной функции и дифференциальной функции плотности распределения

- таблицы частот (статистический ряд)

- эксцесс (центр момент 4-го порядка)

Выборочная дисперсия - среднее арифметическое квадратов отклонения наблюдаемых значений признака 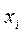от их среднего значения :

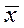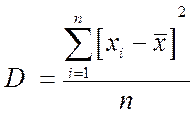
Стандартное (среднее квадратичное) отклонение (СКО) в отличие от дисперсии имеет размерность, равную размерности 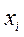. Для выборки (S) и генеральной совокупности ( 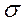)оно определяется соответственно:

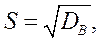
Отсюда выборочная оценка дисперсии D_В часто обозначается S².

Требования к точечным оценкам:

· Несмещённая оценка в среднем совпадает с истинным значением оцениваемого параметра.

· Эффективная оценка характеризуется минимальной дисперсией в сравнении со всеми другими несмещёнными оценками.

· Состоятельная оценка с ростом объёма выборки приближается к истинному значению оцениваемого параметра.

8(9). Расскажите, как и с использованием каких статистических функций программы MS Excel по известной выборке можно быстро и просто определить:

- ширину доверительного интервала или ширину допуска, в который с заданной вероятностью «попадёт» (при правильной настройке) генеральная совокупность, соответствующая этой выборке?

- ширину доверительного интервала для среднего значения этой выборки?