Методические рекомендации.
Трансформатор – это электрическое устройство, состоящее из нескольких индуктивно связанных катушек индуктивности.
I – первичная обмотка трансформатора. К ней подключают источник электроэнергии. Имеет w1 – количество витков индуктивной катушки.
II- вторичная обмотка трансформатора. К ней подключают нагрузку. Имеет w2 – количество витков индуктивной катушки.
Схематичное устройство трансформатора на рисунке 1.
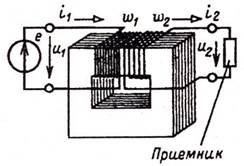
Рисунок 1- Схематичное устройство трансформатора
ЭДС первичной (I) обмотки: е1 = -w1·dф/dt
ЭДС вторичной (II) обмотки: е2 = -w2·dф/dt
Коэффициент трансформации:
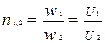
n1,2 > 1 – понижающий трансформатор.
n1,2 < 1 – повышающий трансформатор.
Мощность обмотки: P = I· U·COSφ
Коэффициент полезного действия трансформатора:
КПД = Р2/ Р1=Р2/ Р1 +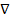 
Р,
где
Р1–мощность первичной обмотки;
Р2- вторичной обмотки;
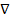Р – потери в трансформаторе.
Задание 1
Трансформатор подключён к линии электропередачи напряжением U=6000В. Определить коэффициент трансформации и число витков первичной обмотки, если известно число витков и напряжение вторичной обмотки.
Таблица1-Данные для расчетов.
| № варианта | U2, В | W2, витков | № варианта | U2, В | W2, витков |
| 1. | 4000 | 800 | 11. | 4100 | 810 |
| 2. | 4010 | 820 | 12. | 4130 | 830 |
| 3. | 4030 | 840 | 13. | 4150 | 850 |
| 4. | 4050 | 860 | 14. | 4200 | 870 |
| 5. | 4070 | 880 | 15. | 4300 | 890 |
| 6. | 4090 | 900 | 16. | 4120 | 920 |
| 7. | 4020 | 910 | 17. | 4130 | 940 |
| 8. | 4040 | 930 | 18. | 4140 | 960 |
| 9. | 4060 | 950 | 19. | 4160 | 980 |
| 10. | 4080 | 970 | 20. | 4180 | 1000 |
Задание 2
Трансформатор подключен к сети переменного тока с напряжением U=400В. Определить напряжение вторичной обмотки трансформатора, если известно количество витков первичной и вторичной обмоток трансформатора w1 и w2 , построить график зависимости U2 от изменения входного напряжения с шагом 50 В от исходного. Данные для расчета в таблице 2.
Таблица 2- Данные для расчета
| № варианта | W1, витков | W2, витков | № варианта | W1, витков | W2, витков |
| 1. | 800 | 50 | 11. | 830 | 61 |
| 2. | 820 | 51 | 12. | 850 | 63 |
| 3. | 840 | 53 | 13. | 920 | 65 |
| 4. | 860 | 55 | 14. | 940 | 67 |
| 5. | 880 | 57 | 15. | 960 | 69 |
| 6. | 900 | 59 | 16. | 980 | 58 |
| 7. | 910 | 60 | 17. | 1000 | 62 |
| 8. | 920 | 52 | 18. | 1010 | 64 |
| 9. | 930 | 54 | 19. | 1030 | 66 |
| 10. | 960 | 56 | 20. | 1200 | 68 |
Контрольные вопросы.
1. На чем основан принцип работы трансформатора?
2. Как называются трансформаторы, если коэффициент трансформации n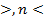 
1?
3. Какое назначение трансформаторов в эл. цепях?
Задание№9.
Расчет трёхфазной электрической цепи.
Схема соединения «треугольник»
Методические рекомендации.
Трехфазной называется система трех ЭДС одинаковой частоты, сдвинутых по фазе друг относительно друга так, что сумма трех углов сдвига равна 2π=360°
При определении параметров цепи пользоваться соотношениями:
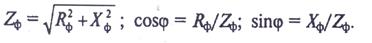
Фазное напряжение: Uф=Uл
Фазный ток: Iф= Uф / Z
Линейный ток: Iл = √3· Iф
Мощности одной фазы:
активная Р = Iф·Uф·cosφ
реактивная Q = Iф · Uф·sinφ
полная S = Iф · Uф
Мощность трехфазной цепи:
активная Р = 3· Iф·Uф·cosφ =√3Iл·Uл·cosφ
реактивная Q = 3·Iф · Uф·sinφ = √3Iл · Uл·sinφ
полная S = 3Iф · Uф = √3Iл · Uл
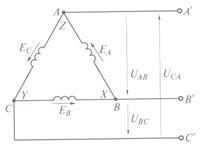
Рисунок 1-Схема трехпроводной трехфазной цепи при соединении «треугольником».
Задание 1
К трехфазной цепи с линейным напряжением Uл = 220В подключена несимметричная нагрузка, фазы которой имеют параметры RA, RвRс
Определить фазные токи, коэффициенты мощности фаз. Нагрузка подключена по схеме «треугольник».
Таблица 1- Данные для расчетов.
| № вар- анта | RА, Ом | Rв, Ом | Rс, Ом | ХLА Ом | ХLВ Ом | ХLС Ом | № вар анта | RА, Ом | Rв, Ом | Rс, Ом | ХLА Ом | ХLВ Ом | ХLС Ом | |
| 1. | 0,1 | 1 | 0,6 | 0,1 | 1,5 | 1,6 | 11. | 0,18 | 1,5 | 0,35 | 0,52 | 1,6 | 1,3 | |
| 2. | 0,12 | 1,1 | 0,59 | 0,2 | 1,4 | 1,2 | 12. | 0,19 | 1,4 | 0,23 | 0,4 | 1,7 | 1,4 | |
| 3. | 0,13 | 1,2 | 0,58 | 0,3 | 1,51 | 1,3 | 13. | 0,3 | 1,51 | 0,28 | 0,41 | 1,8 | 1,5 | |
| 4. | 0,14 | 1,3 | 0,62 | 0,22 | 1,42 | 1,61 | 14. | 0,31 | 1,42 | 0,36 | 0,42 | 1,9 | 1,42 | |
| 5. | 0,15 | 1,4 | 0,54 | 0,33 | 1,52 | 1,52 | 15. | 0,32 | 1,52 | 0,29 | 0,53 | 1,25 | 1,52 | |
| 6. | 0.16 | 1,5 | 0,52 | 0,24 | 1,3 | 1,42 | 16. | 0,34 | 1,3 | 0,37 | 0,43 | 1,35 | 1,3 | |
| 7. | 0,17 | 2 | 0,4 | 0,21 | 1,31 | 1,44 | 17. | 0,35 | 1,31 | 0,41 | 0,51 | 1,38 | 1,31 | |
| 8. | 0,2 | 2,1 | 0,41 | 0,34 | 1,34 | 1,34 | 18. | 0,4 | 1,34 | 0,42 | 0,53 | 1,58 | 1,34 | |
| 9. | 0,22 | 2,2 | 0,42 | 0,25 | 1,46 | 1,38 | 19. | 0,36 | 1,6 | 0,53 | 0,55 | 1,68 | 1,46 | |
| 10. | 0,23 | 1,6 | 0,53 | 0,35 | 1,37 | 1,58 | 20. | 0,41 | 1,7 | 0,43 | 0,58 | 0,1 | 1,37 | |
Задание 2
Симметричный трехфазный потребитель энергии соединен по схеме «треугольник» имеет параметры: линейный токIл, активную мощность P,коэффициент мощности cosφ. Определить Uл, активное фазное сопротивление Rф и реактивное Xф.
Таблица 2- Данные для расчетов.
| № ва- рианта | Iл, А | Р,Вт | cos φ | № ва- рианта | Iл, А | Р,Вт | cos φ |
| 1. | 15,0 | 4800 | 0,6 | 11. | 17,2 | 4830 | 0,61 |
| 2. | 15,2 | 4820 | 0,62 | 12. | 17,4 | 4850 | 0,63 |
| 3. | 15,4 | 4840 | 0,64 | 13. | 17,6 | 4870 | 0,65 |
| 4. | 15,6 | 4860 | 0,66 | 14. | 15,3 | 4890 | 0,7 |
| 5. | 16,0 | 4880 | 0,68 | 15. | 15,5 | 4920 | 0,64 |
| 6. | 16,1 | 4890 | 0,72 | 16. | 16,2 | 4940 | 0,66 |
| 7. | 16,3 | 4900 | 0,74 | 17. | 16,4 | 4960 | 0,77 |
| 8. | 16,5 | 4910 | 0,77 | 18. | 16,8 | 4970 | 0,78 |
| 9. | 17,0 | 4930 | 0,75 | 19. | 14,0 | 4950 | 0,65 |
| 10. | 17,1 | 4950 | 0,63 | 20 | 14,2 | 4920 | 0,69 |
Контрольные вопросы.
1. Какая система называется трёхфазной?
2. Как обозначаются фазы трехфазной системы ЭДС?
3. Какое напряжение называется фазным?
Практическое занятие №10.
Дата: 2018-12-28, просмотров: 265.
