Расчет эквивалентной емкости электрической цепи

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Задание №1.

Расчет эквивалентной емкости электрической цепи.

Методические рекомендации.

Для выполнения данной практической работы необходимо знать расчетные формулы последовательного и параллельного соединения конденсаторов.

Схемы соединения емкостных элементов.

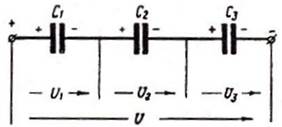
Рисунок 1-Схема последовательного соединения конденсаторов

Последовательное соединение: + +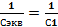

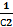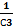
Для схемы из двух конденсаторов: Cэкв =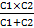

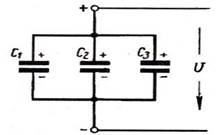
Рисунок 2-Схема параллельного соединения конденсаторов

Параллельное соединение: Cэкв=C1+C2+C3

Требования при выполнении задания.

1. Начертить схему. Обозначить элементы схемы.

2. Переписать условие задания.

3. Указать неизвестные параметры.

4. Решение выполнять поэтапно, вычерчивать схемы замещения и делать пояснения.

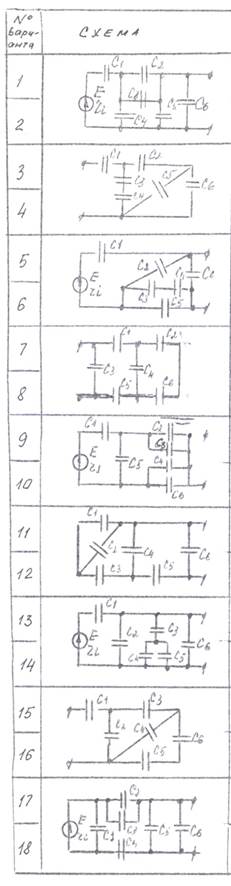
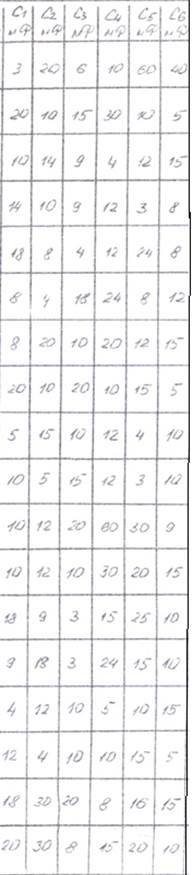
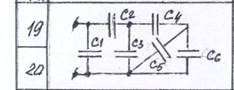
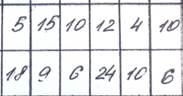
5. Схему и данные для расчетов взять из таблицы 1.

Контрольные вопросы.

1. Назначение конденсаторов.

2. Виды конденсаторов.

3. Единицы измерений электрической ёмкости конденсаторов.

Таблица 1.

Задание№2.

Расчет эквивалентного сопротивления

электрической цепи

Методические рекомендации.

Для выполнения данной практической работы необходимо знать расчетные формулы последовательного и параллельного соединения резисторов.

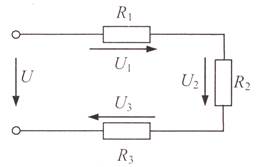
Последовательное соединение:Rэкв = R1+R2+R3

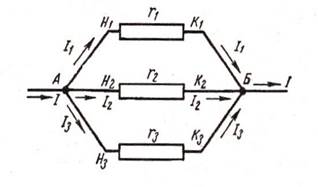
Параллельное соединение: + +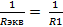

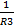
Для схемы из двух резисторов: Rэкв=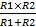

Требования при выполнении задания.

1. Начертить схему. Обозначить элементы схемы.

2. Переписать условие задания.

3. Указать неизвестные параметры.

4. Решение выполнять поэтапно, вычерчивать схемы замещения и делать пояснения.

5. Схему и исходные данные взять из таблицы.

6. Ответить на контрольные вопросы.

Контрольные вопросы.

1. Как на электрических схемах изображаются резисторы?

2. Назначение резисторов?

3. Единицы измерения величины электрического сопротивления?

4. Что называется делителем напряжения?

5. В каких целях применяется делители напряжения?

Таблица №1

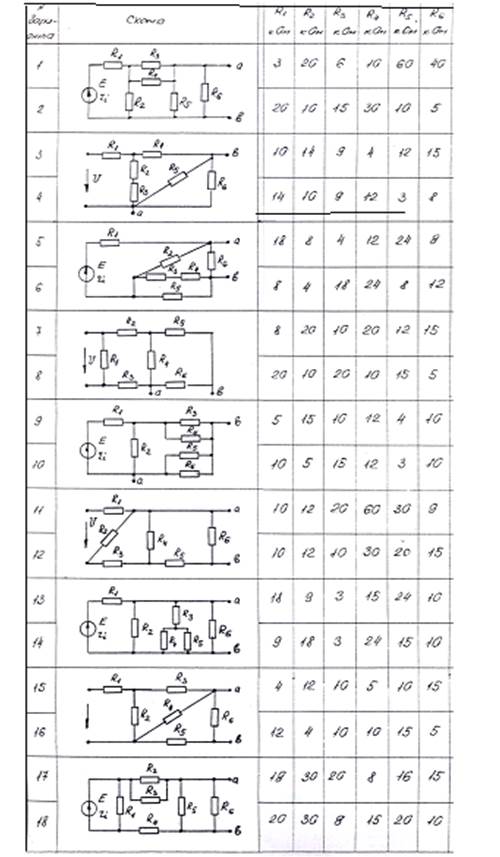
Задание №3.

Расчет сложных электрических цепей с помощью законов Кирхгофа.

Методические рекомендации.

Для выполнения данной практической работы необходимо знать элементы цепи, понятия: ветвь, узел, контур электрической цепи, расчетные формулы последовательного и параллельного соединения элементов, формулировки законов Кирхгофа.

Порядок расчета.

1. Выбрать направление токов в ветвях и направление обхода контуров.

2. Выбрать узлы и составить (n-1) уравнений по I закону Кирхгофа, где n-число узлов в цепи.

3. Выбрать m- простых контуров, составить m уравнений по IIзакону Кирхгофа. При составлении уравнений надо учитывать, что со знаком «+» записываются те ЭДС и токи в ветвях, направление которых совпадает с направлением обхода контуров, а со знаком «-» - не совпадающих с направлением обхода.

4. Подставить численные значения электрических величин и решить систему уравнений.

5. Если в результате расчетов ток получен со знаком «-», значит действительное направление тока противоположно выбранному.

6. Если в ветви направление ЭДС источника противоположно направлению тока, протекающему через источник, то источник работает в режиме потребителя электрической энергии.

Вид системы уравнений с n–неизвестными:

а₁₁х_{1 +}а₁₂х₂ + а₁₃х₃₊……а₁_nх_n= в₁

а₂₁х_{1 +}а₂₂х₂ + а₂₃х₃₊……а₂_nх_n= в₂

а_n₁х_{1 +}а_n₂х₂ + а_n₃х₃₊……а_nnх_n= в_n_,

где:

х₁₌I₁- ток в первой ветви;

х₂₌I₂ – ток во второй ветви;

х_n₌I_n – ток в n- ветви;

а_iy - числовые значения сопротивлений;

в_iy– численные значения ЭДС.

Пример

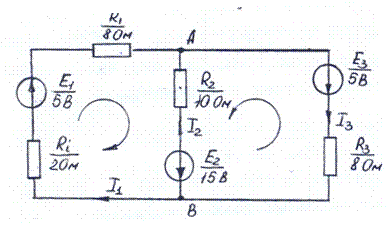
Количество узлов n=2, простых контуров m=2.

Для узла А

0+I₃ = I₁+I₂

Е₁ +Е₂ = I₁(R₁ + R_i) - I₂R₂

Е₂ - Е₃= - I₂R₂- I₃R₃

Подставить численные значения:

I₃=I₁+I₂

5+15= I₁(8 + 2) - I₂ ·10

15-5= - I₂ ·10 - I_3· 8

Преобразование системы:

I₃–(I₁+I₂) =0

20=10 ·I₁ -10 ·I₂

10 = - 10I₂- 8 ·I₃

Решая данную систему, определяются численные значения токов в цепи.

Схему и данные для расчетов взять из таблицы.

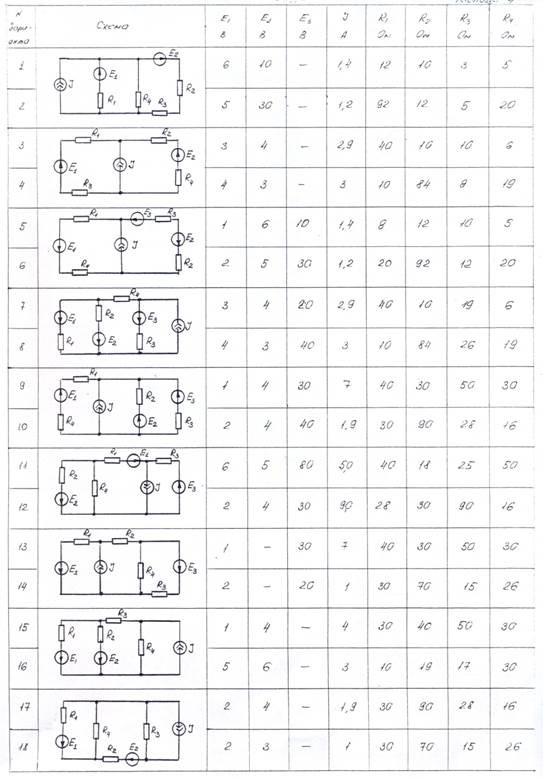
Таблица 1- Данные для расчетов.

Контрольные вопросы.

1. Что такое узел, ветвь, контур электрической цепи?

2. Что такое электрическая схема?

3. Записать формулировку законов Кирхгофа.

4. Написать методику расчетов.

Задание№4.

Задание №5.

Практическое занятие №6.

Задание.

К последовательному колебательному контура подведено напряжение 220 В. Величины активного сопротивления, индуктивности и емкости взять из таблицы и выполнить расчеты:

1) вычислить ток цепи;

2) определить угол φ и характер цепи;

3) построить векторную диаграмму напряжений, определив напряжение на каждом элементе цепи;

4) определить резонансную частоту, добротность колебательного контура. Нарисовать резонансную кривую;

5) определить мощности Р, Q, S;

6) сделать вывод по полученным результатам работы;

7) ответить на контрольные вопросы.

Таблица 1- Данные параметров эл. величин колебательного контура для выполнения расчетов.

№ варианта	_R _{, Ом}	_L _{, мГн}	_C _{, мкФ}	№ варианта	_R _{, Ом}	_L _{, мГн}	_C _{, мкФ}
1.	2	40	180	11.	7	41	200
2.	4	42	184	12.	8	43	202
3.	6	44	186	13.	7,6	45	204
4.	10	46	188	14.	9	47	210
5.	12	48	200	15.	8,5	57	212
6.	15	50	170	16.	9,5	49	220
7.	16	60	174	17.	10,5	59	206
8.	18	62	178	18.	10,8	51	208
9.	20	52	172	19.	11	62	195
10.	2,5	64	178	20.	11,4	53	185

Контрольные вопросы

1. Как определяется период колебаний в эл. цепи?

2. Какие колебания называются незатухающими?

3. Какие основные характеристики последовательного колебательного контура?

4. Как влияет добротность на полосу пропускания и коэффициент передачи?

5. Какой формулой определяется характеристическое сопротивление?

Задание №7.

Задание.

К параллельному колебательному контуры подведено напряжение U=127В частотой 50 Гц Величины активного сопротивления, индуктивности и емкости взять из таблицы и определить:

1) токи всех участков цепи: I_1,I_2,I;

2) мощности;

3) частоту, при которой наступит резонанс токов;

4) построить векторную диаграмму тока. Нарисовать резонансную кривую.

Таблица 1- Данные для расчетов

№варианта	R, Ом	L, мГн	C, мкФ	№варианта	R, Ом	L, мГн	C, мкФ
1.	2	40	180	11.	7	41	200
2.	4	42	184	12.	8	43	202
3.	6	44	186	13.	7,6	45	204
4.	10	46	188	14.	9	47	210
5.	12	48	200	15.	8,5	57	212
6.	15	50	170	16.	9,5	49	220
7.	16	60	174	17.	10,5	59	206
8.	18	62	178	18.	10,8	51	208
9.	20	52	172	19.	11	62	195
10.	2,5	64	178	20.	11,4	53	185

Контрольные вопросы.

1. Что такое полоса пропускания?

2. Что такое расстройка колебательного контура?

3. Какие виды расстроек существуют?

4. Что такое избирательность колебательного контура?

Задание№ 8.

Задание 1

Трансформатор подключён к линии электропередачи напряжением U=6000В. Определить коэффициент трансформации и число витков первичной обмотки, если известно число витков и напряжение вторичной обмотки.

Таблица1-Данные для расчетов.

№ варианта	U₂, В	W₂, витков	№ варианта	U₂, В	W₂, витков
1.	4000	800	11.	4100	810
2.	4010	820	12.	4130	830
3.	4030	840	13.	4150	850
4.	4050	860	14.	4200	870
5.	4070	880	15.	4300	890
6.	4090	900	16.	4120	920
7.	4020	910	17.	4130	940
8.	4040	930	18.	4140	960
9.	4060	950	19.	4160	980
10.	4080	970	20.	4180	1000

Задание 2

Трансформатор подключен к сети переменного тока с напряжением U=400В. Определить напряжение вторичной обмотки трансформатора, если известно количество витков первичной и вторичной обмоток трансформатора w₁ и w_{2 ,} построить график зависимости U₂ от изменения входного напряжения с шагом 50 В от исходного. Данные для расчета в таблице 2.

Таблица 2- Данные для расчета

№ варианта	W₁, витков	W₂, витков	№ варианта	W₁, витков	W₂, витков
1.	800	50	11.	830	61
2.	820	51	12.	850	63
3.	840	53	13.	920	65
4.	860	55	14.	940	67
5.	880	57	15.	960	69
6.	900	59	16.	980	58
7.	910	60	17.	1000	62
8.	920	52	18.	1010	64
9.	930	54	19.	1030	66
10.	960	56	20.	1200	68

Контрольные вопросы.

1. На чем основан принцип работы трансформатора?

2. Как называются трансформаторы, если коэффициент трансформации n 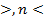1?

3. Какое назначение трансформаторов в эл. цепях?

Задание№9.

Задание 1

К трехфазной цепи с линейным напряжением Uл = 220В подключена несимметричная нагрузка, фазы которой имеют параметры RA, RвRс

Определить фазные токи, коэффициенты мощности фаз. Нагрузка подключена по схеме «треугольник».

Таблица 1- Данные для расчетов.

№ вар- анта	RА, Ом	Rв, Ом	Rс, Ом	Х_LА Ом	Х_LВ Ом	Х_LС Ом	№ вар анта		RА, Ом	Rв, Ом	Rс, Ом	Х_LА Ом	Х_LВ Ом	Х_LС Ом
1.	0,1	1	0,6	0,1	1,5	1,6	11.		0,18	1,5	0,35	0,52	1,6	1,3
2.	0,12	1,1	0,59	0,2	1,4	1,2	12.		0,19	1,4	0,23	0,4	1,7	1,4
3.	0,13	1,2	0,58	0,3	1,51	1,3	13.		0,3	1,51	0,28	0,41	1,8	1,5
4.	0,14	1,3	0,62	0,22	1,42	1,61		14.	0,31	1,42	0,36	0,42	1,9	1,42
5.	0,15	1,4	0,54	0,33	1,52	1,52		15.	0,32	1,52	0,29	0,53	1,25	1,52
6.	0.16	1,5	0,52	0,24	1,3	1,42		16.	0,34	1,3	0,37	0,43	1,35	1,3
7.	0,17	2	0,4	0,21	1,31	1,44		17.	0,35	1,31	0,41	0,51	1,38	1,31
8.	0,2	2,1	0,41	0,34	1,34	1,34		18.	0,4	1,34	0,42	0,53	1,58	1,34
9.	0,22	2,2	0,42	0,25	1,46	1,38		19.	0,36	1,6	0,53	0,55	1,68	1,46
10.	0,23	1,6	0,53	0,35	1,37	1,58		20.	0,41	1,7	0,43	0,58	0,1	1,37

Задание 2

Симметричный трехфазный потребитель энергии соединен по схеме «треугольник» имеет параметры: линейный токIл, активную мощность P,коэффициент мощности cosφ. Определить Uл, активное фазное сопротивление Rф и реактивное Xф.

Таблица 2- Данные для расчетов.

№ ва- рианта	Iл, А	Р,Вт	cos φ	№ ва- рианта	Iл, А	Р,Вт	cos φ
1.	15,0	4800	0,6	11.	17,2	4830	0,61
2.	15,2	4820	0,62	12.	17,4	4850	0,63
3.	15,4	4840	0,64	13.	17,6	4870	0,65
4.	15,6	4860	0,66	14.	15,3	4890	0,7
5.	16,0	4880	0,68	15.	15,5	4920	0,64
6.	16,1	4890	0,72	16.	16,2	4940	0,66
7.	16,3	4900	0,74	17.	16,4	4960	0,77
8.	16,5	4910	0,77	18.	16,8	4970	0,78
9.	17,0	4930	0,75	19.	14,0	4950	0,65
10.	17,1	4950	0,63	20	14,2	4920	0,69

Контрольные вопросы.

1. Какая система называется трёхфазной?

2. Как обозначаются фазы трехфазной системы ЭДС?

3. Какое напряжение называется фазным?

Практическое занятие №10.

Схема соединения «звезда»

Методические рекомендации.

Трехфазной называется система трех ЭДС одинаковой частоты, сдвинутых по фазе друг относительно друга так, что сумма трех углов сдвига равна 2π=360°

При определении параметров цепи пользоваться соотношениями:

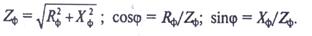
Фазное напряжение Uф=Uл√3

Фазный ток Iф = Uф / Zф

Линейный ток Iл = Iф

Мощности одной фазы:

активная Р = Iф·Uф·cosφ

реактивная Q = Iф · Uф·sinφ

полная S = Iф · Uф

Мощность трехфазной цепи при равномерной нагрузке:

активная Р = 3· Iф·Uф·cosφ =√3Iл·Uл·cosφ

реактивная Q = 3·Iф · Uф·sinφ = √3Iл · Uл·sinφ

полная S = 3Iф · Uф = √3Iл · Uл

S=√ P² +Q² - при неравномерной нагрузке.

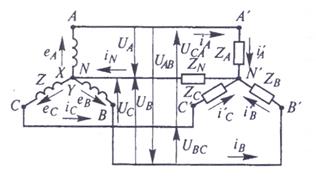
Рисунок 1-Схема трехпроводной трехфазной цепи при соединении «звездой».

Задание 1

В сеть трехфазного тока с линейным напряжением Uл = 280В включен потребитель, соединенный «звездой». Активное сопротивление каждой фазы потребителя R, емкостное сопротивление Хс. Определить линейные и фазные токи и напряжения, активную, реактивную, полную мощность каждой фазы и всей цепи. Данные для решения взять из таблице 1.

Таблица 1- Данные для расчетов.

№ варианта	R., Ом	Хс, Ом	№ варианта	R., Ом	Хс, Ом
1.	10,0	8,0	11.	11,2	9,0
2.	10,2	8,1	12.	11,4	9,2
3.	10,4	8,3	13.	11,6	9,4
4.	10,6	8,5	14.	11,8	9,6
5.	10,8	8,2	15.	10,9	9,8
6.	11,0	8,4	16.	11,9	10,0
7.	10,1	8,6	17.	11,1	9,1
8.	10,3	8,8	18.	11,3	9,3
9.	10,5	8,7	19.	11,5	9,5
10.	10,7	8,9	20.	12,0	9,7

Задание 2

На каждом этаже трехэтажного здания установлено « n»количество ламп, мощностью Р. Определить фазные токи, напряжения в проводах и мощность при полной нагрузке, если линейное напряжениеUл = 380В. Нагрузка соединена по схеме «звезда». Данные для решения взять из таблице 2.

Таблица 2- Данные для расчетов.

№ варианта	n, ламп	Р, Вт	№ варианта	n, ламп	Р, Вт
1.	60	75	11.	99	75
2.	63	60	12.	81	60
3.	66	100	13.	84	100
4.	69	60	14.	87	150
5.	72	75	15.	102	100
6.	75	100	16.	105	60
7.	78	150	17.	108	100
8.	90	100	18.	111	75
9.	93	75	19.	114	100
10.	96	60	20.	127	60

Контрольные вопросы.

1. Как называется провод, подключенный к нулевой точке?

2. Как определяется полная мощность S при неравномерной и равномерной нагрузке эл. цепи?

3. Какое напряжение называется линейным?

Задание №1.

Расчет эквивалентной емкости электрической цепи.

Методические рекомендации.

Дата: 2018-12-28, просмотров: 433.

12 3 Следующая ⇒