Приближенный метод оценки колеблемости вариационного ряда - определение лимита и амплитуды, однако не учитывают значений вариант внутри ряда. Основной общепринятой мерой колеблемости количественного приз­нака в пределах вариационного ряда является среднее квадратичес­кое отклонение ( σ - сигма). Чем больше среднее квадратическое отклонение, тем степень ко­леблемости данного ряда выше.

Методика расчета среднего квадратического отклонения включает следующие этапы:

1. Находят среднюю арифметическую величину (Μ).

2. Определяют отклонения отдельных вариант от средней арифмети­ческой (d=V-M). В медицинской статистике отклонения от средней обозначаются как d (deviate). Сумма всех от­клонений равняется нулю.

3. Возводят каждое отклонение в квадрат d².

4. Перемножают квадраты отклонений на соответствующие частоты d²*p.

5. Находят сумму произведений å( d²*p)

6. Вычисляют среднее квадратическое отклонение по формуле:

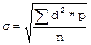 при n больше 30, или  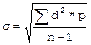при n меньше либо равно 30, где n - число всех вариант.

Значение среднего квадратичного отклонения:

1. Среднее квадратическое отклонение характеризует разброс вариант относительно средней величины (т.е. колеблемость вариационного ряда). Чем больше сигма, тем степень разнообразия данного ряда выше.

2. Среднее квадратичное отклонение используется для сравнительной оценки степени соответствия средней арифметической величины тому вариационному ряду, для которого она вычислена.

Вариации массовых явлений подчиняются закону нормального распределения. Кривая, отображающая это распределение, имеет вид плавной колоколообразной симметричной кривой (кривая Гаусса). Согласно теории вероятности в явлениях, подчиняющихся закону нормального распределения, между значениями средней арифметической и среднего квадратического отклонения существует строгая математическая зависимость. Теоретическое распределение вариант в однородном вариационном ряду подчиняется правилу трех сигм.

Если в системе прямоугольных координат на оси абсцисс отложить значения количественного признака (варианты), а на оси ординат - частоты встречаемости вариант в вариационном ряду, то по сторонам от средней арифметической равномерно располагаются варианты с большими и меньшими значениями.

Установлено, что при нормальном распределении признака:

- 68,3% значений вариант находится в пределах М±1s

- 95,5% значений вариант находится в пределах М±2s

- 99,7% значений вариант находится в пределах М±3s

3. Среднее квадратическое отлонение позволяет установить значения нормы для клинико-биологических показателей. В медицине интервал М±1s обычно принимается за пределы нормы для изучаемого явления. Отклонение оцениваемой величины от средней арифметической больше, чем на 1s указывает на отклонение изучаемого параметра от нормы.

4. В медицине правило трех сигм применяется в педиатрии для индивидуальной оценки уровня физического развития детей (метод сигмальных отклонений), для разработки стандартов детской одежды

5. Среднее квадратическое отклонение необходимо для характеристики степени разнообразия изучаемого признака и вычисления ошибки средней арифметической величины.

Величина среднего квадра­тического отклонения обычно используется для сравнения колеблемости однотипных рядов. Если сравниваются два ряда с разными признаками (рост и масса тела, средняя длительность лечения в стационаре и больничная летальность и т.д.), то непосредственное сопоставление размеров сигм невозможно, т.к. среднеквадратичес­кое отклонение - именованная величина, выраженная в абсолютных числах. В этих случаях применяют коэффициент вариации (Cv), представляющий собой относительную величину: процентное отноше­ние среднего квадратического отклонения к средней арифметической.

Коэффициент вариации вычисляется по формуле:

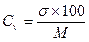
Чем выше коэффициент вариации, тем большая изменчивость данно­го ряда. Считают, что коэффициент вариации свыше 30 % свиде­тельствует о качественной неоднородности совокупности.