Точность измерений выражает степень близости результата измерения к действительному значению измеряемой величины. Учитывая наличие случайных погрешностей в измерениях, эта близость различна для разных результатов. Поэтому точность измерений характеризуют некоторой средней величиной случайной погрешности.

В качестве теоретической характеристики точности измерений чаще всего берут среднее квадратичное отклонение

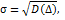(26)

где 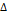— случайная погрешность измерения.

Так как математическое ожидание случайной погрешности равно нулю, т. е. 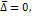то ее дисперсия

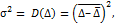(27)

или

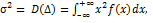(28)

где 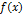— плотность распределения случайной погрешности.

Среднее квадратичное отклонение постоянно 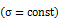для неизменного основного комплекса условий измерений, поэтому оно характеризует условия измерений.

В связи с этим можно дать более широкое, чем раньше, определение равноточности измерений; измерения называют равноточными, если сохраняется постоянство среднего квадратичного отклонения .

Величина является теоретической характеристикой, и ее числовое значение неизвестно. Поэтому пользуются ее приближенным значением — средней квадратической погрешностью, значения которой находят по результатам измерений.

Допустим, что проведено п равноточных измерений и при этом получены случайные погрешности 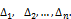Средняя квадратичная погрешность или эмпирическое среднее квадратичное отклонение

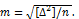(29)

Эта величина также случайная. По закону больших чисел для случайных величин

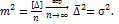(30)

Такие эмпирические характеристики, которые сходятся по вероятности к соответствующим теоретическим характеристикам, называют их состоятельными оценками.

На основании формулы (30) можно принять, что при достаточно большом п

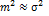(31)

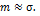(32)

В математической статистике доказывается также, что

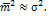(33)

Эмпирические характеристики, математические ожидания которых равны соответствующим теоретическим характеристикам, называют их несмещенными оценками.

Таким образом, по формулам (30) и (33) квадрат средней квадратичной погрешности т2 является состоятельной и несмещенной оценкой дисперсии .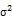

Так как средняя квадратичная погрешность т, вычисляемая по формуле (29), определяет величину с некоторой погрешностью и является величиной случайной, для оценки точности определения самой погрешности т существует формула

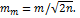(34)

Теоретической характеристикой точности измерений служит также предельная погрешность

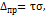(35)

где 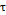— коэффициент, значение которого принимают таким, чтобы была мала вероятность появления погрешности, по абсолютному значению больше предельной, т. е. чтобы была мала величина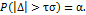

Обычно для 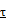берут значения 3; 2,5 или 2. Этим значениям 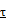соответствуют значения вероятностей 0,003, 0,012, 0,046.

Эти соотношения между значениям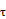и и означают следующее: на каждую тысячу измерений число погрешностей, превосходящих по абсолютному значению предельную 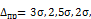в среднем приблизительно равно соответственно 3, 12, 46.

Так как точное значение величины неизвестно, то вместо в формуле (35) берут ее приближенное значение m, получаемое по результатам большого числа измерений, и вычисляют 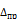по формуле

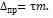(36)

Иногда о точности измерений судят не по значению средней квадратичной или предельной погрешности, а по значению их отношения к измеренной величине. Отношение погрешности к измеренной величине называют относительной погрешностью (средней квадратичной, предельной).

Пример: Угол, точное значение которого 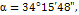измерен шесть раз. Вычислить среднюю квадратическую и предельную погрешности измерения угла. Полученные результаты измерений

и вычислений приведены в таблице 2.