Случайное событие и частность, случайная величина и вероятность.
Теория вероятностей – раздел математики, который по известным вероятностям одних случайных величин определяет вероятности других случайных величин, взаимосвязанных с первыми.
Случайное событие – событие, которое может случиться во время проведения испытания, т.е. оно не закономерно, его нельзя достоверно предсказать заранее.
Случайная величина – такая величина, которая претерпевает случайные изменения от испытания к испытанию (от измерения к измерению). В зависимости от возможных значений случайная величина может быть дискретной или непрерывной. Например, при бросании игральной кости могут выпадать только целые значения (от 1 до 6) – это дискретная случайная величина; а время пробега спортсменом дистанции может изменяться плавно – это непрерывная случайная величина.
Числовые характеристики случайных величин.
Случайной называют такую величину, которая принимает значения в зависимости от стечения случайных обстоятельств. Различают дискретные и случайные непрерывные величины.
Дискретной называют величину, если она принимает счетное множество значений. (Пример: число пациентов на приеме у врача, число букв на странице, число молекул в заданном объеме).
Непрерывной называют величину, которая может принимать значения внутри некоторого интервала. (Пример: температура воздуха, масса тела, рост человека и т.д.)
Законом распределения случайной величины называется совокупность возможных значений этой величины и, соответствующих этим значениям, вероятностей (или частот встречаемости).
Во многих случаях наряду с распределением случайной величины или вместо него информацию об этих величинах могут дать числовые параметры , получившие название числовых характеристик случайной величины. Наиболее употребительные из них:
1.Математическое ожидание - (среднее значение) случайной величины есть сумма произведений всех возможных ее значений на вероятности этих значений:
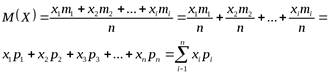
2.Дисперсия случайной величины:
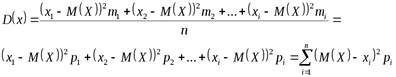
3.Среднее квадратичное отклонение:
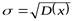
Правило “ТРЕХ СИГМ” - если случайная величина распределена по нормальному закону, то отклонение этой величины от среднего значения по абсолютной величине не превосходит утроенного среднего квадратичного отклонения
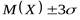
Метод триангуляции
Триангуляция (от лат. triangulum ‒ треугольник), один из методов создания сети опорных геодезическихпунктов и сама сеть, созданная этим методом; состоит в построении рядов или сетей примыкающих друг кдругу треугольников и в определении положения их вершин в избранной системе координат. В каждомтреугольнике измеряют все три угла, а одну из его сторон определяют из вычислений путёмпоследовательного решения предыдущих треугольников, начиная от того из них, в котором одна из его сторонполучена из измерений. Если сторона треугольника получена из непосредственных измерений, то онаназывается базисной стороной Т. В прошлом вместо базисной стороны непосредственно измеряли короткуюлинию, называемую базисом, и от неё путём тригонометрических вычислений через особую сетьтреугольников переходили к стороне треугольника Т. Эту сторону Т. обычно называют выходной стороной, асеть треугольников, через которые она вычислена,‒ базисной сетью. В рядах или сетях Т. для контроля иповышения их точности измеряют большее число базисов или базисных сторон, чем это минимально необходимо.
Т. имеет большое научное и практическое значение. Она служит для: определения фигуры и размеров Землиметодом градусных измерений; изучения горизонтальных движений земной коры; обоснованиятопографических съёмок в различных масштабах и целях; обоснования различных геодезических работ приизыскании, проектировании и строительстве крупных инженерных сооружений, при планировке истроительстве городов и т.д.
При построении Т. исходят из принципа перехода от общего к частному, от крупных треугольников к более мелким. В связи с этимТ. подразделяется на классы, отличающиеся точностью измерений и последовательностью их построения. Вмалых по территории странах Т. высшего класса строят в виде сплошных сетей треугольников. В государствахс большой территорией (СССР, Канада, КНР, США и др.) Т. строят по некоторой схеме и программе. Наиболее стройная схема и программа построения Т. применяется в СССР. На основе рядов и сетей Т. 1-го и 2 го классов определяют пункты Т. 3-го и 4го классов, причём их густотазависит от масштаба топографической съёмки. Например, при масштабе съёмки 1 : 5000 один пункт Т. долженприходиться на каждые 20‒30 км2. В Т. 3-го и 4-го классов погрешности измерения углов не превышаютсоответственно 1,5" и 2,0".
В практике СССР допускается вместо Т. применять метод полигонометрии. При этом ставится условие, чтобыпри построении опорной геодезической сети тем и др. методом достигалась одинаковая точность определенияположения пунктов земной поверхности.
Вершины треугольников Т. обозначаются на местности деревянными или металлическими вышками высотойот 6 до 55 м в зависимости от условий местности.
Метод трилатерации
Трилатерации состоит в определении координат геодезических пунктов, расположенных в вершинах треугольников всей сети, через измерения длин сторон между ними. Характерная схема ряда трилатерации показана на рис.1. По исходным данным известных координат смежных пунктов (А, В), расстоянию между ними (b), а так же по измеряемым длинам сторон и вычисленным горизонтальным проложениям d1, d2, d3 и так далее до другой стороны (b1) ряда между пунктами C и D получают конечный результат. Математический аппарат в виде теоремы косинусов и прямой геодезической задачи позволяет вычислить соответственно неизвестные горизонтальные углы и искомые координаты вершин треугольников.
Ряд трилатераци.
Этот метод может применяться в отдельных случаях при формировании геодезических опорных сетей III, IV классов, сгущения этих опорных сетей до 1, 2 разрядов, сетей съемочной основы для топографических съемок, геодезических изысканий для строительства, при выполнении опорного обоснования при различных инженерно-геодезических работах по возведению мостов, высотных зданий и других работ.
Недостатки:
К сожалению, устройство геодезического обоснования способом трилатерации не находят обширного применения из-за ряда причин:
* при треугольных формах сети отсутствуют избыточные измерения, не дающие возможности возникновению условных уравнений, поэтому иногда приходится выполнять дополнительные измерения для создания необходимых геометрических условий;
* отсутствия контрольных измерений в треугольниках, поэтому для практического использования рекомендуется применение четырехугольников с проведением измерений шести длин сторон (одно будет избыточным и контрольным);
* при линейно вытянутых рядах треугольников трилатерационные сети обладают преобладающим влиянием поперечных погрешностей над продольным отклонением;
* не удобных форм рельефа на местности для ее использования по сравнению с более гибким в этом плане полигонометрическим способом;
* экономического, как более затратного способа, и технического характеров из-за менее точных измерений и результатов.
Метод полигонометрии
Полигонометрия - построение на местности системы ломаных линий, в которой измерены все отрезки линий s и горизонтальные углы β между отрезками. Ломаную линию называют ходом, отрезок s – стороной или линией, β - горизонтальный угол между отрезками – углом поворота. Вершины полигонометрических ходов называют пунктами полигонометрии. Одиночный полигонометрический ход по форме может быть разомкнутым или замкнутым в виде замкнутого многоугольника. Если ход по форме близок к прямой линии, то он называется вытянутым, в противном случае его называют изогнутым.
Система связанных между собой ходов образует полигонометрическую сеть.Отдельный ход между двумя узловыми пунктами или между исходным пунктом и узловой точкой называют звеном. Пункты геодезических сетей на местности закрепляют подземными сооружениями - центрами.Ходы полигонометрии 1 класса прокладывают взамен рядов триангуляции 1 класса. Они строятся в виде полигонов, располагаемых примерно по меридианам и параллелям, с периметром около 800 км. Ходы полигонометрии 1 класса должны быть вытянутыми по форме и состоять не более чем из 10 сторон длиной 20-25 км.
Построение государственной геодезической сети 2 класса методом полигонометрии производится в каждом отдельном случае по особо разрабатываемой программе.Точность измерений углов и линий в полигонометрии 2 класса должна быть в соответствии с величинами, указанными в табл. 1.
При построении геодезических сетей 3 и 4 классов методом полигонометрии определение пунктов производится продолжением одиночных ходов или сетей, опирающихся на пункты высшего класса.Каждое звено сети должно содержать не более двух точек поворота. Минимальная длина сторон в 3 классе - 3 км, в 4 классе - 2 км. Периметр полигонов не должен превосходить в 3 классе 60 км, в 4 классе - 35 км. Углы и линии измеряются с точностью, указанной в табл. 1.
Полигонометрические сети часто создаются для обоснования крупномасштабных съемок, проводимых для специальных целей и для различного рода инженерных работ, связанных с разбивкой сооружений. В этом случае полигонометрия 4 класса развивается по специальным требованиям.
Основные характеристики полигонометрии различных классов
Таблица 1
| Наименование элемента полигонометрии | 1-й класс | 2-й класс | 3-й класс | 4-й класс |
| Периметр полигонов, км | 700-800 | 150-180 | ||
| Длина диагонального полигонометрического хода не более, км | 200 | 60 | 30 | 11-15 |
| Длина стороны хода (звена), км | 8-30 | 5-18 | 3-10 | Не менее 0,25 |
| Число сторон в ходе (звене) не более | 12 | 6 | 6 | 20 |
| Средняя квадратическая ошибка измерения угла, с | 0,4 | 1,0 | 1,5 | 2,0 |
| Средняя квадратическая ошибка измерения длины стороны | 1:400 000 | 1:200 000 | 1:100 000 | 1:40 000 |
Определение превышений и высот точек с помощью спутниковых измерений. Автономное определение высот точек аппаратурой ГЛОНАСС и GPS выполняется с точностью нескольких метров, а определение превышений между точками с точностью 10 15 мм.
Сущность нивелирования заключается в следующем. Если известна абсолютная высота точки А (НА), то для получения высоты точкиВ (НВ) надо проложить нивелирный ход, т.е. измерить превышенияh1 h2 …hn.
Если точки А иВ, расположены так, что измерить между ними превышение с одной установки нивелира невозможно, превышение измеряют по частям (рисунок 10.1).
Рисунок 10.1 - Нивелирный ход
Превышения внутренних участков хода вычисляют по формулам:
| h1= a1b1; | h2= a2b2; | h3= a3b3. | (10.1) |
Превышение между конечными точками хода А иВ равно сумме вычисленных превышений
| hAB = h1 + h2 + h3, | (10.2) |
| а высота точки В определится по формуле: | |
| НВНАh . | (10.3) |
Часть нивелирного хода между двумя прочно закрепленными точками называют секцией. Если нивелируют линию между двумя точками, высоты которых известны, то теоретическую сумму превышений между этими точками получают:
(10.4)
т.е. теоретическая сумма превышений в линии, проложенной между двумя точками с известными высотами, равна разности высот конечной и начальной точек этой линии.
На точность определения превышений геометрическим, а также и тригонометрическим методами влияют кривизна Земли и рефракция (искривление светового луча при прохождении его через слои воздуха различной
105
плотности). Поэтому к превышению прибавляют поправку за кривизну Земли и рефракцию по формуле:
0,43
(10.5)
R
где d – расстояние между точкамиА иВ; R- средний радиус Земли,
Способ красных чисел
Для каждого звена полигона вычисляют красные числа ki, ki,j (i — номер данного полигона, j — номер смежного с ним). Красным числом называется отношение числа станций в звене к числу станций во всем полигоне (или отношение длины звена к периметру полигона).
Сумма красных чисел для каждого полигона должна быть равна единице
Этот способ применяют в том случае, если нет теодолита. С пунктов съемочного обоснования до съемочного пикета измеряют два расстояния.
При построении точки на плане циркулем проводят две дуги, радиусом d1 и d2. На пересечении этих дуг будет находиться съемочный пикет.
Сущность и виды измерений. Погрешности измерений.
Геодезическое измерение, результат измерения, методы и условия измерений. Равноточные и неравноточные измерения
Измерением называется процесс сравнения некоторой физической величины с другой одноименной величиной, принятой за единицу меры.
Единица меры – значение физической величины, принятой для количественной оценки величины того же рода.
Результат измерений – это число, равное отношению измеряемой величины единицы меры.
Различают следующие виды геодезических измерений:
1. Линейные, в результате, которых получают наклонные иррациональные расстояния между заданными точками. Для этой цели применяют ленты, рулетки, проволоки, оптические свето- и радиодальномеры.
2. Угловые, определяющие величины горизонтальных углов. Для выполнения таких измерений применяют теодолит, буссоли, эклиметры.
3. Высотные, в результате, которых получают разности высот отдельных точек. Для этой цели применяют нивелиры, теодолиты-тахеометры, барометры.
Различают два метода геодезических измерений: непосредственные и посредственные (косвенные).
Непосредственные – измерения, при которых определяемые величины получают в результате непосредственного сравнения с единицей измерения.
Косвенные – измерения, при которых определяемые величины получаются как функции других непосредственно измеренных величин.
Процесс измерения включает:
· Объект – свойства которого, например, размер характеризуют результат измерения.
· Техническое средство – получать результат в заданных единицах.
· Метод измерений – обусловлен теорией практических действий и приёмов технических средств.
· Исполнитель измерений – регистрирующее устройство.
· Внешняя среда, в которой происходит процесс измерений.
Совокупность этих элементов, взаимодействуя между собой, образуют условия измерений, которые определяют окончательный результат и его точность. Если измерения происходят в одних и тех же условиях, то их результат называется равноточным. Если хотя бы один из элементов, составляющий совокупность, меняется, то результат измерений неравноточный.
Классификация погрешностей геодезических измерений.
Средняя квадратическая погрешность.
Формулы Гаусса и Бесселя для ее вычисления
Геодезические измерения, выполняемые даже в очень хороших условиях, сопровождаются погрешностями, т.е. отклонением результата измерений L от истинного значения Х нумеруемой величины:
∆ = L-X
Истинное – такое значение измеряемой величины, которое идеальным образом отражало бы количественные свойства объекта. Истинное значение – это понятие гипотетическое, в реальности его достичь невозможно. Это величина, к которой можно приближаться бесконечно близко.
Точность измерений – степень приближения его результата к истинному значению. Чем ниже погрешность, тем выше точность.
Погрешности бывают следующих видов:
Абсолютная погрешность выражается разностью значения, полученного в результате измерения и истинного измерения величины. Например, истинное значение l = 100 м, однако, при измерении этой же линии получен результат 100,05 м, тогда абсолютная погрешность:
E = Xизм – X
E = 100,05 – 100 = 0,05 (м)
Чтобы получить значение достаточно произвести одно измерение. Его называют необходимым, но чаще одним измерением не ограничиваются, а повторяют не менее двух раз. Измерения, которые делают сверх необходимого, называют избыточными (добавочными), они являются весьма важным средством контроля результата измерения.
Абсолютная погрешность не даёт представления о точности полученного результата. Например, погрешность в 0,06 м может быть получена при измерении l = 100 м или l = 1000 м. Поэтому вычисляют относительную погрешность:
C = Eср / X
C = 0,06 / 100 = 1/1667, т.е на 1667 м измеряемой величины допущена погрешность в 1 метр.
Относительная погрешность – отношение абсолютной погрешности к истинному или измеренному значению. Выражают дробью. По инструкции линия местности должна быть измерена не грубее 1/1000.
Погрешности, происходящие от отдельных факторов, называются элементарными. Погрешность обобщенная (Е)– это сумма элементарных.
Возникают:
· грубые (Q),
· систематические (O),
· случайные (∆).
Грубые погрешности измерений возникают в результате грубых промахов, просчётов исполнителя, его невнимательности, незамеченных неисправностях технических средств. Грубые погрешности совершенно недопустимы и должны быть полностью исключены из результатов измерений путем проведения повторных, дополнительных измерении.
Дата: 2019-02-02, просмотров: 419.