Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Для удобства расчетов факторы масштабируют таким образом, чтобы значение верхнего уровня было равно +1, а нижнего –1. С этой целью делают преобразование начала координат факторов и переходят к нормированному (стандартному) масштабу:  

Составление матрицы планирования ПФЭ

План полного факторного эксперимента изображают в виде таблицы, столбцы которой отражают уровни факторов, а строки – номера опытов. Эти таблицы называют матрицами планирования (МП) эксперимента. Поскольку значения уровней факторов по модулю всегда равны единице, то обычно в МП записывают только знак уровня (т. е. «+» вместо «1» и «–» вместо «–1»). 

Матрица планирования для двух факторов приведена ниже:

N	x1	x2	y
1	-	-	y1
2	+	-	y2
3	-	+	y3
4	+	+	y4

 

 

   

 

Если для двух факторов все возможные комбинации уровней легко найти прямым перебором, то с ростом числа факторов возникает необходимость в некотором приеме построения матриц. Рассмотрим прием, основанный на правиле чередования знаков. В первом столбце знаки меняются поочередно, во втором столбце они чередуются через два, в третьем – через 4, в четвертом – через 8 и т. д. по степеням двойки. Так, для трехфакторного эксперимента:

N	x1	x2	x3	y
1	-	-	-	y1
2	+	-	-	y2
3	-	+	-	y3
4	+	+	-	y4
5	-	-	+	y5
6	+	-	+	y6
7	-	+	+	y7
8	+	+	+	y8

 

Влияние факторов на функцию отклика может зависеть от уровня другого фактора, или от сочетания уровней нескольких факторов. Если априорно неизвестно, что такой зависимости между факторами нет, то строят развернутую матрицу планирования, учитывающую не только факторы, но и их взаимодействия. При этом знаки в столбцах для взаимодействий получают перемножением знаков взаимодействующих факторов. Для удобства расчета свободного члена a₀ математической модели в матрицу вводят фиктивный фактор x₀ .

Пример подобной матрицы приведен ниже:

N	x1	x2	x3	x1x2	x1x3	x2x3	x1x2x3	y
1	-	-	-	+	+	+	-	y1
2	+	-	-	-	-	+	+	y2
3	-	+	-	-	+	-	+	y3
4	+	+	-	+	-	-	-	y4
5	-	-	+	+	-	-	+	y5
6	+	-	+	-	+	-	-	y6
7	-	+	+	-	-	+	-	y7
8	+	+	+	+	+	+	+	y8

 

Основные свойства матрицы планирования эксперимента:

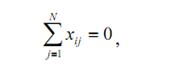а) симметричность относительно центра эксперимента

где i – номер фактора; j – номер опыта; N – число опытов;

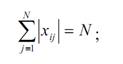б) условие нормировки

в) ортогональность

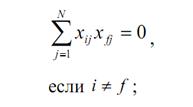г) рототабельность – точки в матрице планирования подбираются так, что точность предсказания значений параметра оптимизации одинакова на равных расстояниях от центра эксперимента и не зависит от направления.

Свойство ортогональности позволяет упростить вычисления и получить независимые оценки коэффициентов регрессии. Это означает, в частности, что замена нулем любого коэффициента в уравнении не изменит оценок остальных коэффициентов. Это свойство может быть полезным, когда точный вид модели не известен и требуется по экспериментальным данным отобрать факторы, существенно влияющие на исследуемый параметр. Если условие ортогональности не выполняется, после исключения каждого незначимого коэффициента необходимо пересчитывать оценки оставшихся коэффициентов и их дисперсии.

Матрица, удовлетворяющая условиям симметричности, нормировки, ортогональности и рототабельности, называется оптимальной.

Матрица планирования полного факторного эксперимента является оптимальной для линейных математических моделей. Если же модель содержит взаимодействия, то свойство рототабельности не выполняется.