ОНИиИД. Лекция 7. ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ
Планирование эксперимента, обработка его результатов, построение уравнений регрессии
Эксперимент – метод исследования, в основе которого лежит целенаправленное воздействие на объект в заданных контролируемых условиях, опосредованное рациональным (в идеале теоретическим) знанием.
Проведение эксперимента в большинстве случаев связано с материальными затратами, отсюда встает задача получения максимума информации об объекте исследования при минимуме материальных затрат. Решением этой задачи и занимается планирование эксперимента.
При исследовании объекта, как правило, не удается выявить и контролировать все факторы, влияющие на исследуемые параметры объекта. Поэтому, исходя из предварительной информации об объекте, выявляют основные влияющие факторы, а воздействие остальных рассматривают как «белый шум», наложенный на истинные результаты эксперимента (так называемая рандомизация эксперимента).
Сущность планирования эксперимента заключается в выборе числа и условий проведения опытов, необходимых и достаточных для решения с требуемой точностью и достоверностью и минимальной стоимостью поставленной задачи.
В результате проведения эксперимента, как правило, требуется получить математическую модель исследуемого объекта. На эмпирическом уровне исследований в качестве математических моделей обычно используют алгебраические полиномы (полиномиальные математические модели). Подобные модели называют так же уравнениями регрессии.
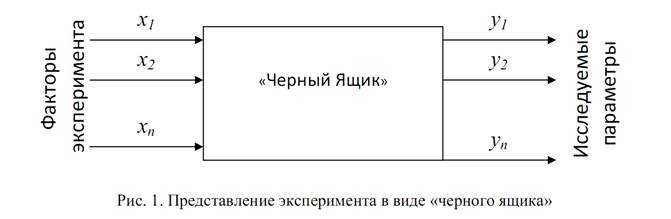
При планировании эксперимента исследуемый объект представляется «черным ящиком» (рис. 1), на который воздействуют факторы xi, и на выходе из которого фиксируются исследуемые параметры уi.
Каждый фактор xi может принимать ряд значений, называемых уровнями факторов. Множество возможных уровней фактора xi называется областью его определения. В общем случае эти области могут быть непрерывными и дискретными, ограниченными и неограниченными. При проведении активного эксперимента должна быть возможность либо изменения уровней факторов в соответствии с планом эксперимента, либо поддержания их на заданном уровне.
При выборе факторов необходимо обеспечить их совместимость и независимость. Совместимость означает возможность сочетания любой комбинации факторов, а независимость – отсутствие между факторами корреляционной связи.
При выборе исследуемых параметров следует обратить внимание на то, чтобы исследуемые параметры существовали при любом состоянии объекта, выражались количественно одним числом и отвечали требованиям статистической однородности, т. е. каждому набору уровней факторов xi с точностью до погрешности эксперимента должно соответствовать определенное значение фактора yi. Кроме того, желательно, чтобы исследуемые параметры были:
- универсальными, т. е. были характерными не только для ис-
следуемого объекта;
- легко вычисляемыми;
- имели физический смысл.
Зависимость исследуемых параметров от уровней факторов называют функцией отклика, а ее геометрическое представление – поверхностью отклика. Пространство, в котором строят эту поверхность, – факторным пространством. Размерность факторного пространства равна числу факторов. Так, например, при двух факторах факторное пространство представляет собой факторную плоскость.
Математическая статистика доказывает, что наиболее адекватно описывают объект математические модели (ММ), полученные в результате эксперимента, план которого удовлетворял следующим критериям:
Критерий ортогональности – когда полученные оценки коэффициентов регрессии некоррелированы. Замена нулем любого коэффициента в ММ в этом случае не изменяет значений остальных коэффициентов.
Критерий рототабельности – когда дисперсия выходной переменной зависит только от расстояния от центра плана.
Критерий A-оптимальности требует выбора такого плана, при котором дисперсионная матрица имеет минимальный след (минимальную сумму диагональных элементов).
Критерий D-оптимальности требует минимизации определителя дисперсионной матрицы.
Критерий G-оптимальности требует достижение наименьшей величины максимальной дисперсии зависимой переменной.
ОНИиИД. Лекция 7. ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ
Планирование эксперимента, обработка его результатов, построение уравнений регрессии
Эксперимент – метод исследования, в основе которого лежит целенаправленное воздействие на объект в заданных контролируемых условиях, опосредованное рациональным (в идеале теоретическим) знанием.
Проведение эксперимента в большинстве случаев связано с материальными затратами, отсюда встает задача получения максимума информации об объекте исследования при минимуме материальных затрат. Решением этой задачи и занимается планирование эксперимента.
При исследовании объекта, как правило, не удается выявить и контролировать все факторы, влияющие на исследуемые параметры объекта. Поэтому, исходя из предварительной информации об объекте, выявляют основные влияющие факторы, а воздействие остальных рассматривают как «белый шум», наложенный на истинные результаты эксперимента (так называемая рандомизация эксперимента).
Сущность планирования эксперимента заключается в выборе числа и условий проведения опытов, необходимых и достаточных для решения с требуемой точностью и достоверностью и минимальной стоимостью поставленной задачи.
В результате проведения эксперимента, как правило, требуется получить математическую модель исследуемого объекта. На эмпирическом уровне исследований в качестве математических моделей обычно используют алгебраические полиномы (полиномиальные математические модели). Подобные модели называют так же уравнениями регрессии.
При планировании эксперимента исследуемый объект представляется «черным ящиком» (рис. 1), на который воздействуют факторы xi, и на выходе из которого фиксируются исследуемые параметры уi.

Каждый фактор xi может принимать ряд значений, называемых уровнями факторов. Множество возможных уровней фактора xi называется областью его определения. В общем случае эти области могут быть непрерывными и дискретными, ограниченными и неограниченными. При проведении активного эксперимента должна быть возможность либо изменения уровней факторов в соответствии с планом эксперимента, либо поддержания их на заданном уровне.
При выборе факторов необходимо обеспечить их совместимость и независимость. Совместимость означает возможность сочетания любой комбинации факторов, а независимость – отсутствие между факторами корреляционной связи.
При выборе исследуемых параметров следует обратить внимание на то, чтобы исследуемые параметры существовали при любом состоянии объекта, выражались количественно одним числом и отвечали требованиям статистической однородности, т. е. каждому набору уровней факторов xi с точностью до погрешности эксперимента должно соответствовать определенное значение фактора yi. Кроме того, желательно, чтобы исследуемые параметры были:
- универсальными, т. е. были характерными не только для ис-
следуемого объекта;
- легко вычисляемыми;
- имели физический смысл.
Зависимость исследуемых параметров от уровней факторов называют функцией отклика, а ее геометрическое представление – поверхностью отклика. Пространство, в котором строят эту поверхность, – факторным пространством. Размерность факторного пространства равна числу факторов. Так, например, при двух факторах факторное пространство представляет собой факторную плоскость.
Математическая статистика доказывает, что наиболее адекватно описывают объект математические модели (ММ), полученные в результате эксперимента, план которого удовлетворял следующим критериям:
Критерий ортогональности – когда полученные оценки коэффициентов регрессии некоррелированы. Замена нулем любого коэффициента в ММ в этом случае не изменяет значений остальных коэффициентов.
Критерий рототабельности – когда дисперсия выходной переменной зависит только от расстояния от центра плана.
Критерий A-оптимальности требует выбора такого плана, при котором дисперсионная матрица имеет минимальный след (минимальную сумму диагональных элементов).
Критерий D-оптимальности требует минимизации определителя дисперсионной матрицы.
Критерий G-оптимальности требует достижение наименьшей величины максимальной дисперсии зависимой переменной.
Дата: 2019-02-02, просмотров: 435.