Решение задач в системе matlab
Лабораторный практикум
Государственное Федеральное бюджетное образовательное учреждение
высшего профессионального образования
Балтийский государственный технический университет «Военмех» им. Д.Ф.Устинова
Кафедра информационных систем и компьютерных технологий
Решение задач в системе matlab
Лабораторный практикум
Санкт-Петербург
2012
Составители: Т.И. Лазарева, доц.; И.В. Мартынова, доц; И.К. Ракова, доц.
УДК 004.438 (075.8)
Решение задач в системе Matlab. Лабораторный практикум / Сост.: Т.И. Лазарева, доц.; И.В. Мартынова, доц; И.К. Ракова, доц., ; Балт. гос. техн. ун-т. – СПб., 2012. – 121 с.
Представленный лабораторный практикум содержит описание пакета Matlab и трех лабораторных работ, а также варианты заданий для выполнения лабораторных работ, требования к ним и контрольные вопросы. Каждая лабораторная работа содержит 10 вариантов индивидуальных заданий.
Лабораторный практикум предназначен для использования в лабораторных работах по дисциплинам «Прикладное программирования» и «Компьютерные технологии».
Рецензент – канд. техн. наук, доцент, проф. каф И3 В.Ю.Емельянов.
Утверждено
редакционно-издательским
советом университета
ã Составители, 2012
ã БГТУ, 2012
Предисловие
Настоящий лабораторный практикум ориентирован на использование пакета Matlab версии 6.5. Он содержит описание пакета Matlab. Материал изложен последовательно, в порядке увеличения сложности.
Студенты имеют возможность сначала ознакомиться с теоретическим материалом. Варианты индивидуальных заданий выдаются заранее с тем, чтобы студенты могли подготовиться к выполнению лабораторных работ. Каждое задание студент должен показать преподавателю, после чего лабораторная работа подлежит защите. К защите студент должен подготовить отчет, включающий в себя титульный лист, формулировку задания, листинг программы или отдельные команды (в зависимости от задания) для решения поставленной задачи, полученные результаты.
Защита лабораторной работы состоит из двух частей: практической и теоретической. В практической части студент должен объяснить работу представленных программ или команд и продемонстрировать свои навыки программирования на языке Matlab, в теоретической – ответить на вопросы по теме работы. При подготовке к защите рекомендуется ответить на контрольные вопросы.
Назначение Matlab
Система Matlab (Matrix Laboratory - матричная лаборатория) разработана компанией MathWork. Это мощная вычислительная система, предназначенная для решения широкого круга математических, инженерных и экономических задач.
Работая в среде Matlab ( ML ), пользователь, не имея специальной программистской подготовки, получает возможность легко и быстро решать вычислительные задачи в различных областях науки и техники (линейная алгебра, теория управления, обработка сигналов и т. п.). Простая командная среда позволяет вводить выражения в форме, близкой к естественной математической записи.
В наибольшей степени система ориентирована на выполнение инженерных расчетов. Математический аппарат оптимизирован на вычисления, проводимые с матрицами и комплексными числами. Matlab содержит множество встроенных функций, необходимых инженеру и научному работнику для выполнения сложных численных расчетов, а также моделирования поведения технических систем и физических процессов.
Кроме того, Matlab имеет мощную графическую систему, которая позволяет визуализировать представление данных, что делает возможным графический анализ результатов.
Все функциональные возможности объединены удобным пользовательским интерфейсом.
Большим плюсом системы является ее открытость и расширяемость. В системе Matlab могут быть написаны программы для многократного использования. Пользователь может не только использовать имеющиеся функции, но и, используя встроенный язык программирования, создавать собственные специализированные функции. ML позволяет работать с программами, написанными на языках Фортран и Си. Большинство специализированных функций хранятся в виде текстовых файлов с расширением m ( m-файлов). Файлы могут быть созданы в редакторе среды Matlab либо во внешнем редакторе, совместимом по кодировке с встроенным редактором. Созданные пользователем m -файлы могут использоваться так же, как и встроенные в Matlab функции.
Помимо работы с программами (функциями), вычисления в ML можно выполнять в режиме ‘’калькулятора’’, т.е. получать результат сразу после ввода очередной команды. Для решения специальных задач с помощью ML разработаны пакеты с дополнительными функциями, которые называются Toolboxes.
Предусмотрена возможность интегрирования системы ML с Microsoft Word и Microsoft Excel.
Интерфейс Matlab 6.5
Работа с файлами
Пункт меню File cодержит следующие команды:
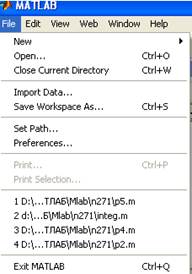 New – m - file – позволяет создать новый m-файл в редакторе ML;
New – m - file – позволяет создать новый m-файл в редакторе ML;
Open – позволяет открыть имеющийся m-файл;
Save Workspace - позволяет сохранить переменные рабочего пространства;
Set Path – позволяет установить путь, указывающий расположение m-файлов;
Preferences – позволяет отображать диалоговое окно, в котором можно настроить различные параметры системы.
В окне пункта меню File отображаются имена 4-х последних файлов, к которым обращался пользователь.
Все файлы, которые будут созданы студентом в ML , должны храниться в предназначенной для этого папке, куда разрешено сохранение файлов: на диске C: (C:\USERS\<папка>) или на сервере ( N :\<папка>) . Всегда есть возможность установить нужный каталог в качестве текущего. Это можно сделать с помощью пункта меню File, Set Path или в окне Current Directory (Текущий каталог).
Команда Exit позволяет выйти из системы.
Редактирование файла
Пункт меню Edit содержит традиционные команды: Undo и Redo (отмена последнего действия и отказ от отмены соответственно), Cut (вырезать фрагмент), Copy (копировать), Paste (вставить), Delete (удалить), Select All (выделить все).
Используя команды Clear Command Window , Clear Command History , Clear Workspace, можно очистить содержимое командного окна, окна истории команд и рабочее пространство соответственно.
Работа с окнами
Пункт меню Window служит для работы с окнами системы. Здесь отображаются команды, соответствующие окнам и программам, которые в данный момент открыты. Выбор одной из этих команд позволяет сделать активным требуемое окно или код программы в редакторе m-файлов.
Справочная система
Пункт меню Help предоставляет доступ к справочной системе программы Matlab .
Командное окно Command Window
Это окно предназначено для ввода чисел, переменных, выражений и команд. Здесь же выводятся результаты работы и сообщения об ошибках. О готовности системы к вводу свидетельствует знак >>, который располагается в текстовом поле командного окна (в командной строке). Для выполнения введенной команды следует нажать клавишу Enter. Пока не нажата клавиша Enter, вводимое выражение может быть отредактировано или удалено. Просмотр содержимого окна можно осуществить, используя полосы прокрутки, а также клавиши < PgUp >, < PgDown >, < Ctrl + Home >, < Ctrl + End >, < Home >, < End >.
Клавиши управления и ¯ в ML имеют совсем другое назначение, чем в текстовых редакторах. Использование этих клавиш позволяет отобразить в командной строке ранее введенные с клавиатуры команды и выражения для их повторного использования. Это возможно потому, что все выполненные команды сохраняются в специальной области памяти. Чтобы стереть содержимое командного окна достаточно набрать и выполнить команду clc .
Рабочая область Workspace
В ML все переменные, используемые в текущем сеансе работы, хранятся в области, называемой рабочей областью или рабочим пространством. Полный перечень используемых переменных отображается в окне Workspace , где можно видеть список текущих переменных и их размеры. Эта информация представлена в виде таблицы, состоящей из следующих столбцов: Name – здесь указывается имя переменной, Size – здесь отображается размер переменной, Bytes – отображается количество выделенной памяти, Class – в этом столбце отображается тип переменной.
Окно Workspace имеет панель инструментов, включающую команды для открытия файлов с данными, создания, сохранения и удаления переменных. Если дважды щелкнуть по строке, соответствующей какой-либо переменной, информация о ней отобразиться в окне Array Editor.
Вычисления в ML
Переменные в ML
В ML, как и в других языках программирования, существует возможность работы с переменными. Любая переменная до использования в формулах должна быть определена. Для этого надо присвоить ей значение. Типы переменных заранее не объявляются. Тип определяется значением, которое присваивается переменной. В качестве оператора присваивания используется знак равенства(=).
>> n=5
n =
5
>> k=0.5
k =
0.5000
По типу переменные могут быть числовые (целые, вещественные, комплексные) или символьные.
Правила составления идентификаторов такие же, как и в ЯВУ (начинается с буквы и может содержать любые комбинации цифр, букв, символа подчеркивания, идентифицируются первые 63 символа, нельзя использовать специальные символы и пробелы, имя переменной должно быть уникальным и не должно совпадать с именами функций). Следует помнить, что строчные и прописные буквы различаются (Abc и abc - разные имена).
Существуют встроенные системные переменные, которые можно использовать, не задавая значения. Они при необходимости могут быть переопределены, т.е. им можно присвоить другие значения, но тогда значения, заданные по умолчанию, будут утеряны.
· pi – число p(p=3.141592653589793);
· eps - погрешность операций над числами с плавающей точкой; очень маленькое значение, равное 2.2*10-16. Её используют, когда надо исключить деление на 0 (например, x /( y + eps ));
· ans - результат последней команды, если в ней нет операции присваивания. Например, если набрали команду 41/75 и не определили, какой переменой присвоить результат, на экране отобразится
ans = 0.5467.
· nan — для обозначения неопределённости результата;
· i , j — мнимая единица( 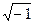 ), используемая для задания мнимой части комплексного числа. Задать комплексные числа можно так:
), используемая для задания мнимой части комплексного числа. Задать комплексные числа можно так:
z = 3+4i
Все эти переменные можно использовать в математических выражениях.
В ML все переменные занимают определенное место в памяти, называемой рабочим пространством системы - Workspace.
ML запоминает значения всех переменных, используемых в текущей сессии. Для того чтобы узнать, какие переменные были задействованы, используется команда who. Чтобы получить более подробную информацию о переменных: размеры, размерность можно использовать команду whos. Эту информацию можно увидеть и в окне Workspace.
Для удаления из памяти всех переменных используется команда clear.
Выборочное удаление переменных можно сделать, применив команду Clear следующим образом: Clear a b.
После завершения сессии ML все переменные рабочего пространства, определенные в текущем сеансе работы, будут потеряны. При необходимости можно сохранить значения переменных в файле. Для этого нужно выбрать пункт меню File , Save Workspace As, далее в диалоговом окне задать имя файла для сохранения данных. Результаты будут сохранены в бинарном файле с расширением mat. Для восстановления значений переменных в следующем сеансе работы необходимо выбрать File , O ре n , имя файла. В результате все переменные станут доступны.
Другой способ сохранения и восстановления переменных рабочего пространства - набрать команды:
Save имя файла. mat и Load имя файл a . mat соответственно.
Всю сессию (все, что отображается в командном окне) можно сохранить и поместить в текстовый файл. Для этого необходимо выполнить следующую команду:
diary <имя>.txt
Эта команда начинает запись сессии в текстовый файл. По команде diary off запись прекращается. Команда diary on возобновляет запись.
Задание векторов и матриц
Способы задания векторов.
Вектор - это одномерный массив данных. Вектор в ML - это матрица из одного столбца или одной строки. Соответственно вектор может быть вектором – столбцом или вектором – строкой.
Для задания вектора можно воспользоваться одним из приведенных ниже способов.
· Можно задать значения вектора поэлементно:
<имя пер.>=[<значение1> <значение2> ….<значение N >]
Например,
>>P=[3 5 7 12]
Значения элементов записываются через пробел или через запятую.
В результате выполнения этой команды создается вектор – строка.
P =
3 5 7 12
Если при задании вектора значения его элементов разделить точкой с запятой, то получим вектор-столбец.
<<A=[1; 2; 3]
A=
1
2
3
· Если элементы вектора являются арифметической прогрессией, то можно задать вектор так:
<имя пер.>=<нач. значение>:<шаг>:<конечное значение>
Например,
>>X=0 : 0.5: pi
В результате будет сформирован вектор со значениями:
X =
0 0.5000 1.0000 1.5000 2.0000 2.5000 3.0000
Шаг должен быть больше нуля. Если он равен единице, то его можно не указывать.
>>Х = 1 : 10
X =
1 2 3 4 5 6 7 8 9 10
Чтобы изменить форму вектора, надо записать Х’ – тогда вектор отобразится в виде столбца. Такая операция называется транспонированием.
Например,
>> X=1:1:5
X = 1 2 3 4 5
>> X'
ans =
1
2
3
4
5
· Также для формирования арифметической прогрессии можно использовать функцию linspace
linspace (<нач. значение>,<кон. значение>,<кол. значений>)
Например,
>>B=linspace(0,pi,5)
B =
0 0.7854 1.5708 2.3562 3.1416
· Вектор можно задать также путём объединения нескольких векторов.
Например,
>>A=[1 2 3]; B=[4 5 6]; C=[7 8 9]; D=[A B C]
D =
1 2 3 4 5 6 7 8 9
Для определения длины вектора предназначена функция l ength.
>> l=length(D)
l =
9
Для доступа к элементу вектора необходимо указать его имя и в круглых скобках номер элемента. Например, D(3). Для обращения к последнему элементу вектора можно записать: D(length(D)) или D(end).
Задание матриц
При задании матриц данные строк записываются через пробел или через запятую. Элементы разных строк разделяются знаком точка с запятой (;) или записываются с новой строки. В ML матрица хранится в порядке следования по столбцам.
Зададим матрицу:
>>A=[1 2 3; 4 5 6;7 8 9]
A =
1 2 3
4 5 6
7 8 9
или
>> A=[1 2 3
4 5 6
7 8 9]
A =
1 2 3
4 5 6
7 8 9
Обращение к элементу матрицы: <имя> (<индексы>), например, А(2,3).
Операции в ML
В ML можно не только выполнять обычные арифметические операции над числами и вычислять значения функций, но и производить операции над векторами и матрицами.
Операции отношения
К операциям отношения в M L относятся:
равно(= =), не равно( ~ =), меньше (<), меньше или равно(<=), больше (>), больше или равно (>=).
Операции отношения используются для поэлементного сравнения 2 операндов (чисел, матриц, векторов одинакового размера). Результатом операции отношения может быть соответственно число, матрица или вектор, состоящие из элементов, обозначающих «истина» или «ложь». В ML это 1 и 0 соответственно.
>>A=[1 0 3; -2 5 -6];
>> B=[8 -9 1; 7 2 2];
>> A>B
ans =
0 1 1
0 1 0
В результате получили матрицу, каждый элемент которой имеет значение «истина» или «ложь».
>> x=1; y=2; z=3;
>> ((x+y)==z)+(y<z)+(x<=y)
ans =
3
Логические операции
В ML существует возможность представления логических выражений с помощью логических операторов и логических операций. Логические операции предназначены для выполнения поэлементных логических операций над векторами и матрицами одинаковых размеров. К логическим операциям относятся:
логическое И (&), логическое ИЛИ (|), логическое НЕ ( ~ ).
Вместо логических операций можно пользоваться логическими операторами (функциями) and , or , not соответственно. Логические операторы определены над матрицами одинаковой размерности и выполняются над каждым из элементов.
В логических выражениях используются логические операции и операции отношения.
Приоритет операций в ML
Приоритет операций определяет порядок действий в выражении. Его можно изменять с помощью круглых скобок. Далее представлены операции в порядке убывания приоритета:
1. логическая операция НЕ (~);
2. транспонирование(.’, ’),возведение в степень(.^, ^);
3. унарный плюс (+), унарный минус (-);
4. умножение и деление(.*, ./, .\, *, /, \);
5. сложение и вычитание (+, -);
6. операции отношения (<, >, <=, >=, ==, ~=);
7. логическая операция И(&);
8. логическая операция ИЛИ(|);
Элементарные функции
В ML существует большое количество элементарных математических функций для выполнения действий с числами: тригонометрические, степенные, логарифмические и экспоненциальные и функции округления. Каждая функция обладает именем и списком аргументов, которые задаются в круглых скобках и, если их несколько, перечисляются через запятую.
Тригонометрические функции
Существуют встроенные тригонометрические и гиперболические функции sin ( x ), cos ( x ), tan ( x ), cot ( x ), asin ( x ), acos ( x ), atan ( x ), acot ( x ), sinh ( x ) и т. д.. Аргументы этих функций могут задаваться в радианах и в градусах (в следующих версиях, начиная с версии 7.0). У функций в градусной мере после названия функции добавляется буква d. s in(x)- аргумент в радианах, а sind(x) – аргумент в градусах
Некоторые часто используемые математические функции:
· exp ( x ) –экспонента числа x;
· log(x) – натуральный логарифм;
· log10(x) – десятичный логарифм;
· sqrt(x) – квадратный корень;
· abs ( x ) –абсолютное значение x;
· real ( z ) – вещественная часть комплексного числа;
· imag ( z ) - мнимой часть комплексного числа;
· mod ( x , y ) - остаток от целочисленного деления;
· round ( x ) – округление до ближайшего целого.
Для работы с датами можно воспользоваться функциями:
· calendar – выводит календарь на текущий месяц;
· date –выводит текущую дату.
Все элементарные функции, приведенные выше, можно применять к векторам и матрицам. Если введен вектор X , то задав функцию Y = sin ( X ), получим вектор, элементами которого будут значения синусов элементов исходного вектора.
>> X=[1 2 3 4];
>> Y=sin(X)
Y =
0.8415 0.9093 0.1411 -0.7568
Информацию о любой функции ML можно получить, выполнив команду: help <имя функции>.
Особые матрицы
B ML можно не только задавать матрицы своими значениями или формировать их по формулам, но можно с помощью специальных функций получать особые матрицы:
· матрица случайных чисел
rand ( n , m ) - формирует матрицу из n строк и m столбцов, заполненную случайными равномерно распределенными числами в интервале от 0 до 1.
rand ( n ) — формирует квадратную матрицу случайных чисел.
>>A=rand(3)
A =
0.9501 0.4860 0.4565
0.2311 0.8913 0.0185
0.6068 0.7621 0.8214
Можно задавать размер матрицы, используя вектор из двух элементов, равных числу строк и столбцов. Например,
>> B=rand([3 4])
B =
0.9501 0.4860 0.4565 0.4447
0.2311 0.8913 0.0185 0.6154
0.6068 0.7621 0.8214 0.7919
Если надо сгенерировать матрицу такого же размера, как и существующая матрица, то необходимо выполнить команду:
>> rand(size(A))
ans =
0.4103 0.3529 0.1389
0.8936 0.8132 0.2028
0.0579 0.0099 0.1987
size(A) — функция, возвращающая размер матрицы А в виде вектора.
· магический квадрат (матрица, у которой суммы элементов в строках, столбцах и диагоналях одинаковы) - magic(n,m)
>> magic(3)
ans =
8 1 6
3 5 7
4 9 2
· единичная матрица - eye(n,m)
>> eye(3)
ans =
1 0 0
0 1 0
0 0 1
· матрица из 0 – zeros(n,m)
>> zeros(3)
ans =
0 0 0
0 0 0
0 0 0
· матрица из 1 – ones(n,m)
>> ones(3)
ans =
1 1 1
1 1 1
1 1 1
· диагональная матрица
Чтобы получить диагональную матрицу необходимо задать вектор, количество элементов которого определит размерность матрицы. Значения вектора расположатся на главной диагонали.
>> V=[1 2 3 4 5];
>> diag(V)
ans =
1 0 0 0 0
0 2 0 0 0
0 0 3 0 0
0 0 0 4 0
0 0 0 0 5
· выделение диагонали из матрицы
>> diag(A)
ans =
0.9501
0.8913
0.8214
Результат – вектор столбец, состоящий из элементов, расположенных на главной диагонали. Иными словами при использовании этой функции, если параметром является матрица, то результат – вектор, а если параметром является вектор, результат – матрица.
Для увеличения быстродействия работы программы, бывает полезно заранее задать размерность матрицы, для этого создать матрицу с нулевыми элементами - zeros(n,m), а затем заполнять ее значениями.
Добавим строку к матрице А
>>A=[1 2 3;4 5 6;7 8 9];
Зададим вектор В
>> B=[5 5 5];
Запишем:
>> A=[A;B]
Получим новую матрицу размером 4х3
A =
1 2 3
4 5 6
7 8 9
5 5 5
Удалим из матрицы 2 столбец
>> A(:, 2)=[]
A =
1 3
5 5
Можно удалить элемент из матрицы.
A (3)=[] – удаление 3-го элемента матрицы.
>> A=[1 2 3;4 5 6;7 8 9]
A =
1 2 3
4 5 6
7 8 9
>> A(3)=[]
Результат – вектор А, состоящий из элементов матрицы в порядке следования по столбцам без элемента А(3,1)
A =
1 4 2 5 8 3 6 9
Удаление матрицы из памяти
>> clear A
Графика в ML
Система М L обладает мощными графическими возможностями. Вывод графической информации ML осуществляет в отдельное окно, которое создается автоматически, когда используется какая-либо графическая функция. Для оформления и редактирования графиков предусмотрены специальные команды.
Диаграммы
Диаграммы позволяют представить векторные и матричные данные в более наглядном виде.
Для построения столбиковой диаграммы используется функция bar(<вектор> ).
Пусть имеем вектор Y. Построим столбиковую диаграмму.
>>Y=[2 5 3 7];
>> bar(Y)
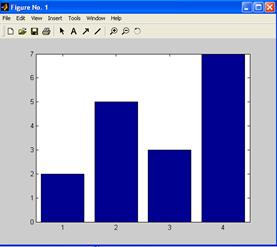
Каждый элемент представляется в виде столбца, высота которого пропорциональна его значению. На оси x – номера элементов.
Зададим два вектора X и Y . Они должны быть одной длины.
>>Y=[2 5 3 7];
>>X=[8 10 4 1];
>> bar(X ,Y)
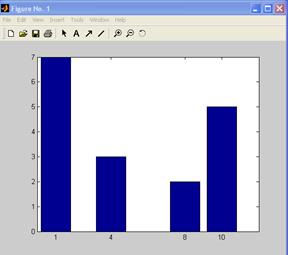
В этом случае по оси y откладываются значения вектора y, а по оси х - не номера элементов, а значения вектора х.
В качестве аргумента функции bar можно задать матрицу:
>> A=[1 2 3; 4 5 6; 7 8 9];
>> bar(A)
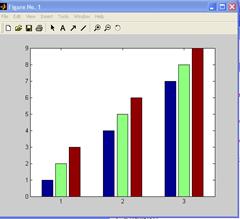
Чтобы отобразить функцию в виде диаграммы нужно получить два вектора (вектор значения аргумента и вектор значения функции) и применить к ним команду bar.
>>X=0: 0.1: 5;
>>Y=exp(x);
>>bar(X, Y);
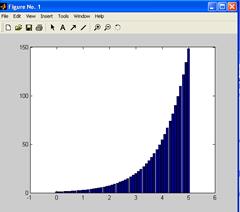
Для получения объемной диаграммы используется команда bar 3:
>>A=[1 2 3; 4 5 6; 7 8 9];
>> bar3(A);
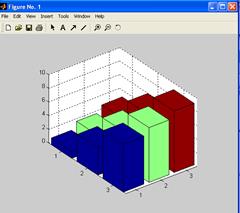
При использовании функции barh ( A ) получим диаграмму с горизонтально расположенными столбцами.
Круговые диаграммы.
Использование круговой диаграммы можно показать на примере определения доли (в процентах) каждого элемента вектора от общей суммы элементов.
Круговые диаграммы строятся с помощью функции pie (<вектор>).
>>X=[3 8 10]
>>pie(X)
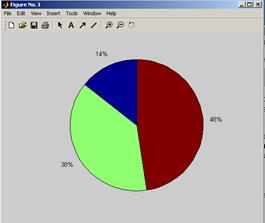
Построение секторов ведется, начиная от вертикальной оси против часовой стрелки.
Чтобы выделить какой-либо сектор, необходимо создать дополнительно вектор из 0 и 1 такого же размера, что и вектор, содержащий данные. Наличие 1 показывает, что надо отделить сектор с таким же номером единичного элемента, что и в этом векторе Y. Пусть заданы два вектора X и Y .
>>X=[16 8 3 1 4];
>>Y=[0 1 0 0 1];
>> pie(X, Y)
Единица в векторе Y показывает, что второй и последний сектора должны быть отделены.
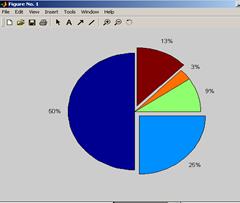
Можно построить объемную диаграмму, применив функцию pie3(<вектор a >).
>>pie3(X, Y)
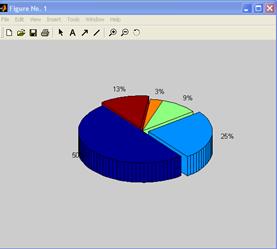
Трехмерная графика.
График поверхности (трехмерный график) – это график, положение точки в котором определяется значениями трех координат. Трехмерным аналогом функции plot является функция plot 3, которая позволяет создавать трехмерные линии. Если есть три вектора x , y , z, задающих координаты точек в трехмерном пространстве, то при выполнении функции plot 3( x , y , z ), построится трехмерная линия на плоскости.
Пусть требуется построить график линии, заданной формулами:
x=2sin(t+ p /2),
y=2cos(t+ p /2),
z = t , где t принадлежит диапазону [0, 8 p ]
>> t=0:pi/100:8*pi;
>> x=2*sin(t+pi/2);
>> y=2*cos(t+pi/2);
>> z=t;
>> plot3(x,y,z);
>> axis square;
>> grid on
Построилась винтовая линия (спираль).
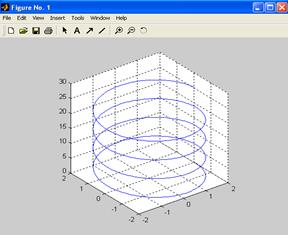
Функция plot 3, также как и функция plot, может иметь дополнительный аргумент, задающий параметры линии (тип линии, цвет и тип маркера). Например, plot 3( x , y , z , ‘ g *’).
Можно также использовать команду ezplot 3:
>> ezplot3('cos(2*pi*t)','sin(2*pi*t)','t',[-2,2])
Для вычерчивания каркасных поверхностей в трехмерном пространстве существуют две основные функции: mesh и surf .
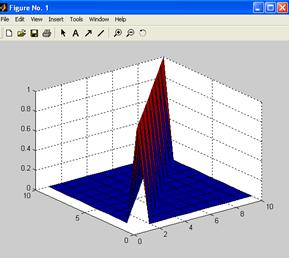
Команда mesh ( Z ) – строит прозрачную сетчатую поверхность, а команда surf ( Z )- затененную, где Z - матрица, значения элементов которой определяют соответствующие координаты на графике. Построим прозрачную поверхность для единичной матрицы, задав команды:
>>Z=eye(8);
>>mesh(Z)
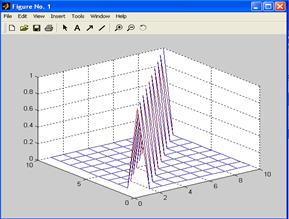
По главной диагонали расположены “пики” – единицы.
Аналогично, задав команду:
>>surf(Z)
Получим затененную поверхность.
Для построения в трехмерном пространстве функции от 2-х переменных Z (X, Y ) необходимо сначала с помощью векторов x и y задать прямоугольную сетку, которая будет использоваться как основание для построения трехмерной поверхности. Для этого надо воспользоваться функцией meshgrid, которая создает эту сетку из точек в прямоугольной области с заданными интервалами. Диапазоны значений по осям x и y задаются векторами x и y соответственно. Имена векторов и матриц могут различаться.
Пусть значения по осям x и y заданы векторами x и y:
>> x=[1 2 3];
>> y=[4 5 6];
Сформируем матрицы X и Y с помощью функции meshgrid :
>> [X,Y]=meshgrid (x,y)
X =
1 2 3
1 2 3
1 2 3
Y =
4 4 4
5 5 5
6 6 6
На основе векторов x и y формируются две матрицы, в которые записываются координаты узлов сетки. Матрица X содержит одинаковые строки, в которых заданы координаты X . Матрица Y содержит одинаковые столбцы, в которых заданы координаты Y . Наложение матриц X и Y позволяет получить пары (xi и yj), для которых в дальнейшем вычисляется значение функции Z. Значения функции в узлах сетки записываются в матрицу Z , размерность которой равна размерности матриц X и Y .
Построим график функции, которая имеет вид:
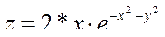 на заданном интервале от-2 до 2 и от y от -4 до 4 с шагом равным 0.1
на заданном интервале от-2 до 2 и от y от -4 до 4 с шагом равным 0.1
Зададим два вектора x и y, используя запись:
>>x =-2 : 0.1: 2;
>>y =-4 : 0.1 :4;
Далее вызывается команда
>>[X, Y]=meshgrid(x, y)
Значения векторов можно указать прямо внутри команды meshgrid(-2:0.1:2,-4:0.1:4)
Если оба вектора одинаковые, то можно записать: [X, Y]= meshgrid(x )
Создаётся прямоугольная сетка с шагом 0.1, которая используется для построения 3-х мерной поверхности. Каждому значению x ставится в соответствие каждое значение y. Для каждой пары xi yi,, (в узлах сетки) будет вычислено значение функции Z . В результате сформируется матрица из вычисленных значений функции. После этого можно вызвать команду для вывода изображения на экран.
Ниже приведен пример построения графика с использованием функции plot 3:
>>x=-2:0.1:2;
>>y=-4:0.1:4;
>>[X, Y]=meshgrid(x, y);
>>Z=2*X.*exp(-X.^2 - Y.^2);
>>plot3(X, Y, Z)
>>grid
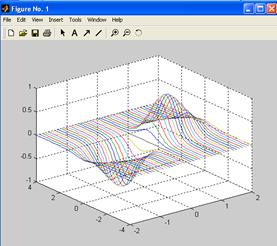
Более наглядные графики получаются с использованием функции mesh .
>> mesh(X,Y,Z)
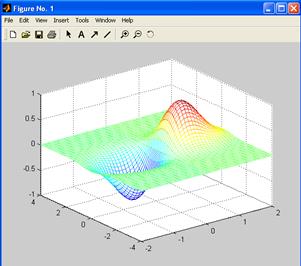
Линии на разных участках графика окрашены в разные цвета. Эти цвета соответствуют значениям функции. По умолчанию оттенки красного цвета соответствуют большим значениям функции, а синего – меньшим.
Можно сделать “прозрачной” каркасную поверхность, отобразив ее скрытые части, применив команду hidden off . Отмена - hidden on.
Если использовать функцию meshz (X, Y , Z ), то будет видно основание, на котором построен график.
Пример построения сферы.
Пусть необходимо начертить поверхность, которая не может быть представлена выражением z = f ( x , y ), например, сферу x 2 + y 2 + z 2 =1. В этом случае параметры поверхности можно задать, используя подходящую координатную систему, например, сферические координаты. Можно взять в качестве параметров вертикальную координату z и полярную координату q на плоскости
x - y.
Если r обозначает расстояние до оси z , то тогда выражение для сферы становится r 2 + z 2 =1 или  отсюда
отсюда 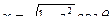 ,
, 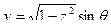
Построение сферической поверхности можно выполнить командами:
>>[z,t]=meshgrid(-1: 0.1: 1, (0:0.1:2)*pi);

Вектор значений Z Вектор значений t от 0 до 2 π
>>x=sqrt(1-z.^2).*cos(t);
>>y=sqrt(1-z.^2).*sin(t);
>>surf(x,y,z)
>>axis square
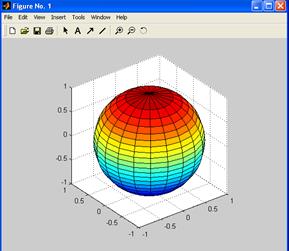
Все трехмерные графики, которые мы строили, можно было видеть только из одной точки обзора, т.е. позиции, с которой мы видим трехмерное изображение. В ML можно изменять точку обзора. Эта точка характеризуется двумя параметрами: азимутом (Az ) и углом возвышения (El ). Азимут определяет угол поворота вокруг оси z и отсчитывается от оси, противоположной y, в направлении против часовой стрелки. Угол возвышения – это угол между отрезком, направленным из начала координат в точку обзора, и плоскостью xy. Точку обзора можно менять программно, используя функцию view ( Az , El ) или более просто, используя специальную кнопку на панели инструментов графического окна Figure – Rotate 3-D.
Программирование в ML
Система ML предоставляет пользователю для решения различных задач мощный язык программирования высокого уровня, понятный непрофессиональным программистам. До сих пор все вычисления и операции мы производили в режиме прямых вычислений. Для эффективной работы с большими наборами команд этого недостаточно. Гораздо лучше было бы записать этот набор команд в виде программы и сохранить ее на диске. Программа представляет собой последовательность команд, записанных на языке ML (программный код), и сохраняется на диске в виде m - файла.
Создать m - файл можно с помощью любого текстового редактора, но в ML предусмотрен собственный встроенный редактор EDITOR , который имеет удобные средства для создания и отладки программ. Написанный текст программы студенты должны сохранять в файле на диске, куда разрешена запись, задав ему имя (имя файла и имя каталога не должны содержать русских букв). Этот файл будет иметь расширение .m. Чтобы войти в текстовый редактор, надо выбрать пункт меню File , New , m - file. В редакторе m- файлов можно не только набрать текст программы, но и запустить ее на выполнение. Для сохранения программы на диске надо выбрать пункт меню File , Save as , <имя m -файла>.
m - файлы могут быть двух видов:
· файл-программа, или Script -файл (Script m - File );
· файл-функция (Function m-File).
Файлы-программы называют Script -файлами или сценариями. Они состоят из последовательности команд и не имеют входных и выходных параметров. Они обычно используются для автоматизации выполнения большого набора команд. Вызов Script -файла осуществляется просто указанием его имени.
В файлах- функциях описываются функции, определяемые пользователем. Они могут иметь входные и выходные значения. Обращение к файлу-функции осуществляется указанием имени и в круглых скобках списка параметров.
Операторы языка
Программа может иметь комментарии. Символ % означает, что далее следует поясняющий текст. Все комментарии начинаются с этого знака. Комментарий не является исполняемым оператором.
Вывод комментариев на экран при выполнении программы обеспечивает оператор echo on. Отменяет вывод комментариев на экран оператор echo off. Оператор pause приостанавливает выполнение программы и ожидает нажатия любой клавиши для продолжения. Оператор pause(n) создает паузу в n секунд.
Операторами языка можно пользоваться как при создании программ, так и в режиме прямых вычислений.
Операторы ввода/вывода
Интерактивное взаимодействие пользователя с программой реализуется с помощью операторов i nput и display.
Оператор i nput (<текст> ) обеспечивает ввод данных с клавиатуры. Текст, указанный в качестве параметра, заключается в апострофы. Он отображается на экране при вводе. Обращение к этой функции имеет вид:
<имя переменной>= i nput (‘<текст>’)
Например, при выполнении команды x = input (‘вв. x = ’) на экран выводится текст ’вв. х=’ и ожидается ввод данных с клавиатуры. Введенное данное присваивается переменной х.
При наборе в командном окне:
>> r=input('Введите радиус ');
На экране получим:
Введите радиус
Далее ожидается ввод значения переменной r .
Если в текст выводимой строки ввести символы '\ n ’, то курсор будет перемещен на следующую строку.
>> r=input('Введите \n радиус ');
Введите
радиус=
Оператор display (<параметр>) или disp (<параметр> ) выводит значение переменной или константы.
disp(A) – выведет матрицу А, причем выводятся только значения элементов, а текст ‘А=’, выводится не будет.
disp(‘Привет’) - на экране будет выведено слово Привет
Оператор цикла с параметром
Оператор цикла позволяет описывать действия, которые выполняются фиксированное количество раз.
for <параметр цикла>=<начальное значение>:<шаг>:<конечное значение>
<операторы>
End
Для досрочного прерывания цикла, используется оператор break.
Если шаг изменения параметра цикла равен 1, то его можно не указывать. Параметры цикла, их начальное и конечное значения и шаг изменения, могут быть целого и вещественного типа.
Например, требуется вычислить значения у=x2 для всех х на отрезке от 1 до 10 c шагом равным 3.
>>for x=1:3:10
y=x^2
end
Результат выполнения данного оператора:
y =
1
y =
16
y =
49
y =
100
Или вычислим значения у для всех х на отрезке от 0.1 до 1 c шагом равным 0.5.
>> for x=0.1:0.5:1
y=x^2
end
В результате получили:
y =
0.0100
y =
0.3600
Везде, где возможно, в ML следует использовать не циклы, а векторные и матричные операции (т.к. это быстрее).
Пусть требуется составить вектор из 5 нечетных чисел натурального ряда. В ML решать эту задачу можно 3 способами:
· Первый способ - использовать оператор цикла
>> for i =1:5
x(i)=2*i-1
end
На экране получим:
x =
1
x =
1 3
x =
1 3 5
x =
1 3 5 7
x =
1 3 5 7 9
Этот способ очень неэффективен по времени, т.к. память не выделяется сразу под весь массив, а при каждой итерации цикла заново создается вектор х с размерностью на единицу большей, чем на предыдущем шаге, что и приводит к большим затратам времени. Это показывает распечатка результов.
· Второй способ - сформировать вектор из нулей х=zeros(1,5), а потом заполнить его значениями.
>> x=zeros(1,5)
x =
0 0 0 0 0
>> for i=1:5
x(i)=2*i-1
end
В результате получим:
x =
1 0 0 0 0
x =
1 3 0 0 0
x =
1 3 5 0 0
x =
1 3 5 7 0
x =
1 3 5 7 9
В данном случае мы заранее определили размер вектора, в который записываются результаты работы цикла. Этот способ несколько быстрее первого.
· Третий способ - можно сформировать два вектора:
вектор i =1:5 и вектор х=2* i -1
>> i=1: 5
i =
1 2 3 4 5
>> x=2*i-1
x =
1 3 5 7 9
В данном случае применяются векторные операции вместо использования циклов, и этот способ самый быстрый.
Чтобы повысить эффективность работы программы, следует иметь в виду следующее правило: везде, где возможно, заменять фрагменты программы, содержащие циклы for и while на матричные операции или матричные функции. Это объясняется тем, что скорость выполнения матричных и векторных операций выше.
Если нельзя обойтись без циклов, то можно заставить их выполняться быстрее, если следовать правилу: создавать заранее каждый вектор, в который требуется записывать результат работы цикла.
End
Сформируем вектор нечетных чисел:
>>x=zeros(1, 5)
>> i=1;
>> while i<=5
x(i)=2*i-1;
i=i+1;
end;
x =
1 3 5 7 9
Как видим, такой способ получения последовательности нечетных чисел тоже возможен, но он также является неэффективным, т. е. медленным.
Найти наибольшее число, факториал которого< 150.
>>echo on
%нахождение наибольшего числа, факториал, которого меньше 150
>>i=1;
f=1;
while f<150
i=i+1;
f=f*i;
end
disp(i-1)
на экране получим:
5
или можно воспользоваться встроенной функцией:
>> i=1;
while prod(1:i)<150
i=i+1;
end;
disp(i-1)
на экране получим:
5
Условный оператор
Условный оператор позволяет организовать ветвления в программе и имеет следующую синтаксическую конструкцию:
if (<логическое выражение1>)
<операторы>
[ elseif (<логическое выражение2>)
<операторы>
elseif (<логическое выражение3>)
<операторы>
…]
[ else
<операторы>]
End
В этой конструкции может быть произвольное количество вложений ветвей elseif или их может не быть вовсе.
Пусть необходимо по введенной с клавиатуры температуре воздуха охарактеризовать погоду. Введем следующий текст:
>> t=input('введи температуру')
if (t<0)
s='мороз'
elseif and(t>0,t<=10)
s='холодно'
elseif and(t>10,t<=20)
s='тепло'
else
s='жарко'
end
В результате выполнения этих команд получим на экране:
введи температуру (например, ввели -4) -4
t =
-4
s =
мороз
Логическое выражение может быть записано и в такой форме:
(t>0)&(t<=10)
Оператор переключения (выбора)
Если необходимо сделать множественный выбор, можно воспользоваться оператором переключения, синтаксическая конструкция которого приведена ниже.
Switch <ключевое выражение>
Case { <список значений1}
<операторы>
Case {<список значений2>}
<операторы>
…….
[ Otherwise
<операторы>]
End
Сначала вычисляется значение ключевого выражения. Затем это значение ищется в списках значений. Если совпадение найдено, то выполняются операторы соответствующего блока, в противном случае выполняются операторы, стоящие после ключевого слова otherwise .
Пусть необходимо по введенному с клавиатуры номеру месяца вывести название времени года. Ниже приведены команды, позволяющие решить эту задачу.
>>n=input('введи номер месяца : ')
switch n
case {1,2,12}
disp('зима')
case {3,4,5}
disp('весна')
case {6,7,8}
disp('лето')
case {9,10,11}
disp('осень')
otherwise
disp('ошибка')
end
На экране получим:
введи номер месяца : 11
n =
11
осень
Функция eval
В ML имеется возможность сформировать требуемую команду в виде строки символов, а затем выполнить ее, как обычную команду, набранную в командном окне. Для этого предназначена встроенная функция eval.
Метод задания команд в виде текстовых строк и их выполнения с помощью этой функции, используется при написании m-файлов, т. к. такой метод позволяет реализовывать более эффективные алгоритмы решения задач.
Функция еval (<текст>) предназначена для выполнения команды, заданной текстом, как команды ML.
Например, eval (‘2*2+3’) выводит на экран 7. Аргументом функции может быть также строковая переменная.
Команда eval (‘<имя скрипт-файла>’) вызовет выполнение операторов, находящихся в файле с соответствующим именем.
Функция menu
Эта функция предназначена для вывода на экран окна с выпадающим меню, которое имеет заголовок и кнопки с названиями пунктов меню. Количество кнопок, равное количеству пунктов меню, определяется количеством параметров функции menu.
k = menu(‘<заголовок меню>’,’<назв. пункта 1>’,…,’<назв. пункта n >’)
Номер выбранной кнопки является результатом функции menu.
Пример.
Пусть необходимо построить график функции на заданном интервале от 0 до 2 pi , цветом, выбранным из меню.
Напишем script-файл:
k=menu ('цвет','красный', 'зеленый','синий')
color=['r'
'g'
'b'];
t=0:0.1:2*pi;
s=sin(t);
plot(t,s,color(k))
При выполнении этого скрипт-файла функция menu выводит на экран окно вида:

При нажатии на одну из кнопок с названием цвета, номер этой кнопки становится результатом функции menu и попадает в переменную k. Вектор-столбец color содержит атрибуты цвета для построения графика. По номеру k нужный атрибут выбирается из массива color и указывается в команде plot. В результате, выбрав нужный пункт меню, получим график функции, построенный выбранным цветом.
Для организации многократного выбора и выполнения нужных действий с помощью меню можно использовать цикл while и функцию eval . Для этого команды, реализующие необходимые действия, оформляются в виде скрипт-файлов: для каждого пункта меню – свой скрипт-файл , затем необходимо задать символьную матрицу, например, D, состоящую из названий файлов, соответствующих пунктам меню (заданий). Строки символьной матрицы должны иметь одинаковую длину. Команда return обеспечивает возврат из функции или скрипт-файла в точку вызова. В данном примере можно также использовать команду break, которая предназначена для досрочного прерывания цикла. Предположим, что необходимо выполнить по выбору 3 задания в любом порядке.
D=[‘f1 ’
‘f2 ’
'f3 '
‘return‘];
n=1;
while n<4
n=menu(‘меню’, ’пункт1’, ’пункт2’, ’пункт3’, ’выход’)
eval(D(n,:))
end
Каждая строка символьной матрицы D содержит имя одного из файлов, реализующих соответствующий пункт меню. В n – ой строке матрицы находится название файла, выполняющего n –й пункт меню. Обращение D ( n ,:) позволяет извлечь из матрицы D n -ую строку, содержащую название файла. В результате выполнения команды menu в n записывается номер выбранного пункта меню. Для выполнения файл-программы достаточно в командной строке указать имя этого скрипта. Функция eval с параметром D ( n ,:) запускает соответствующий скрипт-файл для выполнения.
Script -файлы
Файл-программы (их называют скриптами или сценариями) являются самым простым типом m-файлов. Script - файл состоит из последовательности команд, не содержит заголовка, а также входных и выходных параметров. Все объекты, используемые внутри script -файла, считаются глобальными. Если в рабочем пространстве есть данные, то внутри script-файла их можно использовать, а после окончания выполнения script - файла можно использовать данные, созданные с его помощью. Такие файлы используются для автоматизации выполнения большого набора инструкций.
В одной строке программы можно размещать несколько операторов, тогда они разделяются либо запятой, либо точкой с запятой. Если оператор длинный и не умещается на одной строке, то в конце строки ставятся три точки и дальше на другой строке продолжается набор этого оператора.
Для выполнения файл-программы достаточно в командной строке указать имя этого скрипта. Перед запуском программы на выполнение необходимо установить свой каталог в качестве текущего. Запуск файла на выполнение можно осуществить двумя способами:
1. из окна редактора;
2. из командного окна.
Для запуска программы на выполнение из окна редактора надо выбрать пункт меню Debug , Run , или нажать функциональную клавишу F 5, или выбрать соответствующую пиктограмму на панели инструментов. Выполнить программу, уже сохраненную на диске, можно из командного окна ML, просто набрав имя файла без расширения.
Создадим script -файл, в который поместим текст программы, позволяющей вычислить длину окружности по величине ее радиуса.
В текстовом редакторе наберем следующий текст:
% Вычисление длины окружности
r=input (‘Введите радиус окружности ’)
l=2*pi*r;
disp(‘Длина окружности равна’)
disp(l)
Сохраним его на диске с именем dl _ okr в своей папке. Затем вызовем его для выполнения, указав в окне Command Window в командной строке имя файла dl _ okr .
>> dl_okr
Получим на экране:
Введите радиус окружности 12
r =
12
Длина окружности равна
75.3982
Файлы-функции
Система ML позволяет описать свои пользовательские функции и обращаться к ним, как к встроеннным. В отличие от script-файла файл - функция имеет входные параметры и может передавать результат в виде выходных параметров. Файлы-функции часто применяют при решении задач вычислительной математики.
Можно создавать файл-функцию с любым количеством входных и выходных параметров. Файл-функция всегда состоит из заголовка и тела функции.
Заголовок функции:
function [<список вых. параметров >]=<имя функции >(<список вх. параметров>)
Заголовок функции включает ключевое слово function , имя функции, входные и выходные параметры. После заголовка записываются операторы, реализующие алгоритм поставленной задачи. Они составляют тело функции.
Если функция содержит только один выходной параметр, то квадратные скобки не нужны, а если несколько, то они указываются через запятую в квадратных скобках, образуя вектор. Переменным из списка выходных параметров присваиваются значения, вычисленные в функции. Список входных параметров указывается через запятую в круглых скобках после имени функции. Имя m -файла, в котором сохраняется текст функции должно совпадать с именем функции. Имя функции не несёт результата.
При вызове файл-функции нужно указать ее имя и список фактических параметров. Это можно осуществить либо в командном режиме, либо из других файл-программ или файл-функций.
Вызов (активизация) файла-функции c одним выходным параметром может иметь вид:
<имя функции>(<список входных фактических параметров>)
и может использоваться в операторах присваивания или в выражении::
<имя переменой>=<имя функции>(<список входн. фактических пар-ов>)
Выходных параметров может быть столько, сколько необходимо, тогда список выходных параметров перечисляется через запятую в квадратных скобках:
function [< z 1, z 2,…, zn >]=<имя функции >(< список входных. параметров >)
<операторы, в результате которых выходные параметры получают значения>
Вызвать такую функцию можно так:
[ y 1, y 2,…, yn ]=<имя функции >(<список вх. факт. параметров>)
Все переменные, используемые внутри файла-функции, а также входные и выходные параметры являются локальными. Они доступны только внутри функции.
Напишем файл-функцию, позволяющую вычислить факториал любого числа.
Не будем использовать оператор цикла, а используем функцию prod (1: n ). В редакторе наберем следующий текст:
%нахождение факториала любого числа
function f=fact orial (x)
f=prod(1:x);
Сохраним файл на диске с именем factorial. Этот файл получит расширение .m. Обратимся к функции для вычисления факториала числа 5:
>> factorial(5)
ans =
120
или
>> f=factorial(5)
f =
120
Отличия файла-функции от Scipt -файла:
1. Файл-функция имеет входные и выходные параметры, а scipt -файл - нет;
2. Все переменные, используемые внутри файла-функции, локальны. Файл-программа работает с переменными рабочего пространства, т.е. в scipt -файле можно использовать глобальные данные;
3. Функция перед выполнением компилируется. Scipt -файл не компилируется целиком, а выполняется в режиме интерпретации.
4. Имя файла, в котором записана функция, должно совпадать с именем функции, а имя scipt -файла может быть любым.
Программа будет выполняться быстрее, если вместо script -файла использовать файл-функцию (в случае, если это возможно).
Вычисление интеграла.
Самым простым численным методом нахождения определенных интегралов является метод трапеций, который реализован функцией trapz ( x , y ), где x и y – вектора, задающие значения аргумента и функции в пределах интегрирования. Для ее использования не требуется оформление подинтегральной функции в качестве файла-функции.
Вычислим интеграл 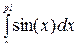
>> x=0:pi/100:pi;
>> y=sin(x);
>> z=trapz(x,y);
z =
1.9998
Получили приближенное значение интеграла. Увеличив шаг интегрирования до pi/1000, получим более точное значение – 2.
Более точные методы реализованы в функциях quad , quad 8, quadl .
Функция quad основана на квадратурной формуле Симпсона, а функция quadl предназначена для вычисления интеграла по более точным формулам Гаусса-Лейбница. Функция quad 8 реализует метод Ньютона-Котеса восьмого порядка. Все три функции имеют одинаковый набор параметров.
[i, n]=quad(fun, a, b, tol, trace), где
fun - имя файла-функции или символьное выражение, определяющее подинтегральную функцию (оно должно быть заключено в апострофы);
a , b – пределы интегрирования;
tol – погрешность вычислений;
trace – признак; если его значение равно 1, то при выполнении функции строится график подинтегральной функции, если 0, то не строится. Последние два параметра являются необязательными.
i – значение интеграла;
n – количество значений функции, которое потребовалось вычислить для нахождения значения интеграла.
>> [i, n]=quad8('func', 0, pi, 1e-8, 1)
i =
7.1938
n =
33
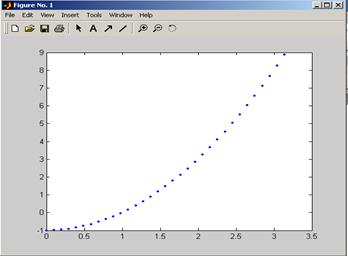
При использовании этих численных методов задаётся требуемая точность вычислений, а шаг подбирается автоматически (в отличие от функции trapz). По умолчанию точность равна 10-6.
Имя функции может быть задано символьным выражением.
>> [i,n]=quad8('sin(x)', 0, pi, 1e-8, 0)
i =
2.0000
n =
33
Такой же результат получим, если не укажем два необязательных параметра:
>> [i, n]=quad8('sin(x)', 0, pi )
i =
2.0000
n =
33
Тот же интеграл можно вычислить с использованием функции quadl:
>> [i, n]=quadl('sin(x)',0,pi,1e-8,0)
i =
2.0000
n =
48
Для достижения одной и той же точности понадобилось различное количество вычислений. Можно при вызове функции не указывать выходной параметр n. Тогда команда обращения к функции будет:
>> i=quadl('sin(x)', 0, pi, 1e-8, 0)
i =
2.0000
В этом случае не используется количество значений функции, которое потребовалось вычислить для нахождения значения интеграла.
Fzero(fun, x0, tol, trace),
где
fun - имя файл-функции или символьное выражение (формула), заключенные в апострофы;
х0 – начальное значение х, от которого начнётся процесс;
tol – погрешность вычислений;
trace – признак; если значение 1, то график строится, если 0, то не строится.
tol и trac е являются необязательными параметрами.
Если корней несколько, то задавая различные начальные значения, можно найти различные корни.
Например, построим график функции sin(x)/(x*2) на отрезке [-10 1]).
>> s='sin(x)/(x*2)'
>>fplot(s, [-10 1])
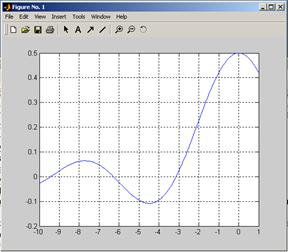
При различных начальных значениях получаем различные корни.
>> fzero(s, -7)
ans =
-6.2832
>> fzero(s, -4)
ans =
-3.1416
Нахождение минимума функции на заданном отрезке.
Вычисление локального минимума функции одной переменной на заданном отрезке выполняет функция fminbnd . При использовании функции поиска минимума рекомендуется предварительно построить график исследуемой функции, чтобы точнее определить отрезки поиска минимума.
[x, y] = fminbnd(fun, a, b), где
fun – имя функции или символьное выражение (формула), заключенное в апострофы;
a, b – границы отрезка, на котором ищется минимум;
Результат – вектор, состоящий из двух значений:
x –аргумент функции (вычисленное значение), при котором достигается минимум;
y – значение функции в точке минимума;
Пример.
Для функции sin(x)/(x*2) найти локальный минимум на отрезке
[-10 1], вывести значение функции в этой точке и построить график.
>> [x,y]=fminbnd('sin(x)/(x*2)',-10,1)
x =
-4.4934
y =
-0.1086
Если хотим получить только значение аргумента, при котором функция будет иметь минимальное значение, то обращение к функции будет:
>> fminbnd('sin(x)/(x*2)',-10,1)
ans =
-4.4934
или
>> x=fminbnd('sin(x)/(x*2)',-10,1)
x =
-4.4934
>> ezplot('sin(x)/(x*2)',-10,1)
>> grid on
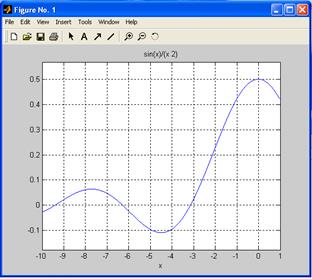
Для нахождения локального максимума не предусмотрено специальной функции. Можно найти максимум, используя fminbnd для функции, имеющей обратный знак.
Задание №1.
Вычислить N значений функции на заданном отрезке.
На экран вывести значения аргумента и значения функции.
Варианты
Функция Отрезок Количество разбиений
1. 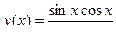 [0,2
[0,2 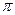 ] N=10
] N=10
2. 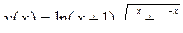 [-0.2,4] N=9
[-0.2,4] N=9
3. 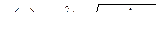 [0,0.3] N=7
[0,0.3] N=7
4. 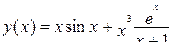 [0,1] N=10
[0,1] N=10
5. 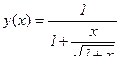 [0,3] N=8
[0,3] N=8
6. 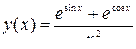 [
[ 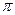 ,3
,3 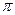 ] N=8
] N=8
7.  [-1,1] N=7
[-1,1] N=7
8. 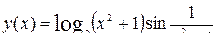 [-1,1] N=10
[-1,1] N=10
9. 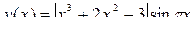 [-2,2] N=7
[-2,2] N=7
10. 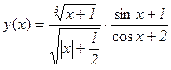 [-2,2] N=9
[-2,2] N=9
Задание №2.
Для заданных векторов a и b длины n (значения элементов векторов и их длину студент задает сам) выполнить преобразования и вычисления в соответствии с вариантом.
Варианты
1. В векторе a элементы с номерами от n 1 до n 2 удвоить, а в векторе b элементы с этими же номерами заменить их средним арифметическим.
2. Образовать новый вектор c=[a1,a2,…,an,b1,b2,…,bn], определить его максимальный и минимальный элементы и поменять их местами.
3. Образовать вектор c =[a1,a2,a3,b4,b5,…,bn] и упорядочить его по возрастанию и убыванию.
4. Образовать вектор c =[a3,a4,…,an,b1,b2,b3] и переставить элементы вектора c в обратном порядке. Результат записать в новый вектор.
5. Получить вектор x, содержащий удвоенные значения элементов вектора a, и вектор y, содержащий утроенные значения элементов вектора b. Определить среднее арифметическое каждого вектора.
6. Вычислить среднее арифметическое элементов двух векторов. Заменить минимальный элемент первого вектора на максимальный элемент второго вектора.
7. Получить два новых вектора, состоящих из элементов исходных, начиная с номера n 1 до номера n 2. Найти сумму минимальных элементов новых векторов.
8. Заменить нулем минимальный элемент вектора a и максимальный элемент вектора b.
9. Вычислить произведение элементов векторов с номерами от n 1 до n 2. Найти минимальные значения векторов и заменить последние элементы векторов их минимумами.
10. Образовать вектор c =[a2,a3,a4,b3,b4,…,bn]. Элементы с номерами от n 1 до n 2 заменить средним арифметическим этих элементов.
Задание №3.
При помощи встроенных функций для заполнения стандартных матриц, индексации двоеточием и, возможно, объединения, поворота или транспонирования получить следующие матрицы. Применить функции обработки данных и поэлементные операции для нахождения заданных величин.
Варианты
1. A= 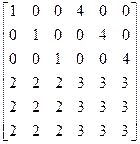
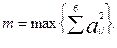
2. A= 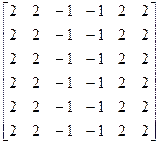
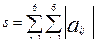 .
.
3. A= 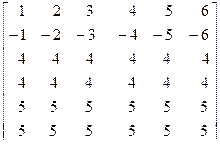
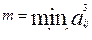 .
.
4. A= 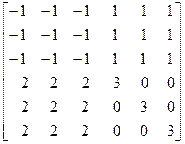
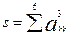
5. A= 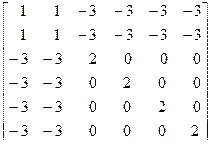
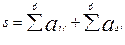
6. A= 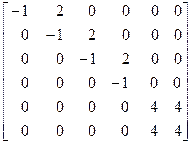
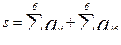
7. A= 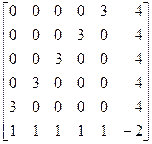
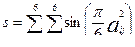
8. A= 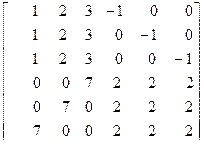
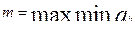
9. A= 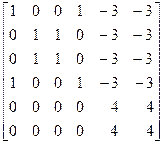
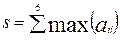
10. A= 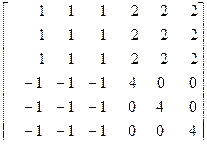
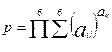
Задание №4.
4.1.Построить графики двух функций на заданных отрезках.
Вывести графики:
• в разных окнах
• в одном окне в одних осях
• в одном окне в разных осях
Использовать различные цвета, стили, подписи, легенду. Нанести сетку.
Варианты
Функция f Функция g Аргумент x
1. 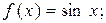

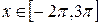
2. 
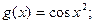
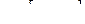
3. 
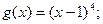
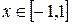
4. 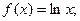
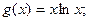
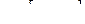
5. 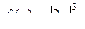
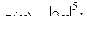
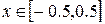
6. 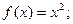
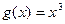
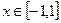
7. 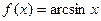
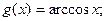
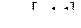
8. 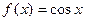
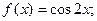
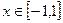
9. 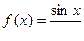
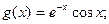
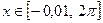
10. 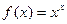

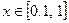
4.2.Построить график кусочно-заданной функции, отобразить ветви разными цветами и маркерами.
Варианты
1 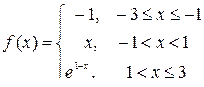
2 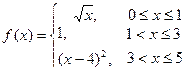
3 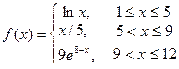
4 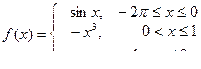
5 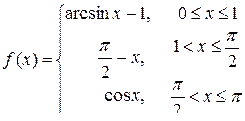
6 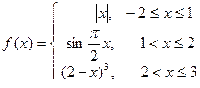
7 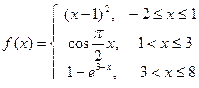
8 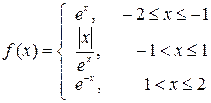
9 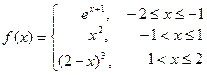
10 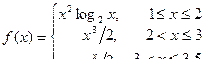
Задание №5.
Построить график функции двух переменных.
Варианты
Функция z Аргумент x Аргумент y
1. 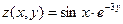
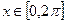
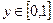
2. 
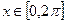
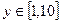
3. 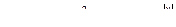
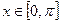
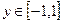
4. 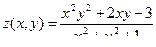
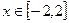
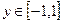
5. 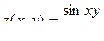
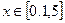
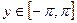
6. 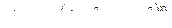
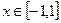
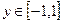
7. 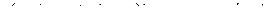
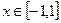
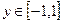
8. 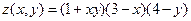
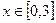
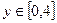
9. 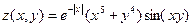
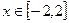
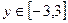
10. 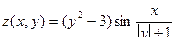

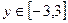
Задание №6.
Написать скрипт-файл для решения следующих задач.
Варианты
1. По заданному вектору определить номер его элемента с наибольшим отклонением от среднего арифметического всех элементов векторов.
2. Найти среднее арифметическое элементов заданного вектора и заменить первый элемент этим значением.
3. Вычислить максимальное значение среди элементов главной диагонали заданной матрицы.
4. Переставить первый столбец квадратной матрицы со строкой, где находится наименьший элемент.
5. Сложить все элементы заданной матрицы, кроме элементов главной диагонали.
6. Заменить максимальный элемент вектора средним значением всех его элементов.
7. Заменить элемент матрицы с индексами 1,1 произведением всех элементов матрицы.
8. Заменить последний элемент вектора на максимальный элемент.
9. Найти значение и номер максимального элемента. Графически отобразить элементы заданного вектора синими маркерами, а максимальный элемент – красным.
10. Упорядочить элементы вектора по убыванию, затем последний элемент заменить на среднее арифметическое всех элементов вектора.
Лабораторная работа №2
Решение типовых вычислительных задач в системе MAtlab
Цель работы – научиться использовать встроенные функции, реализующие различные численные методы решения, а также средства отображения результатов расчета; освоить создание файлов-сценариев и файлов-функций.
Постановка задачи – Каждый вариант задания состоит из пяти пунктов:
1. вычисление корней полинома;
2. решение системы линейных уравнений;
3. вычисление локального минимума и максимума функции;
4. вычисление определенного интеграла.
5. решение трансцендентного уравнения;
Согласно варианту индивидуального задания требуется написать пять программ, соблюдая приведенные ниже указания к выполнению лабораторной работы:
· Для каждого пункта задания создать свой скрипт-файл.
· Написать файл-сценарий (script - файл), в котором пользовательский интерфейс оформлен в виде меню. Выбранный пункт меню определяет выполнение файла, соответствующего пункту индивидуального задания. При написании программы для реализации меню использовать встроенную функцию menu(), оператор цикла с предусловием while и функцию eval ().
· Уравнения и функции для выполнения пунктов задания № 3, 4, 5 описать в виде файлов – функций.
· Для пункта 1 при вычислении корней полинома построить график полинома и отобразить на нем найденные действительные корни. Ввод границ построения графика должен осуществляться пользователем с клавиатуры.
· Для пункта задания №2 при решении системы линейных уравнений осуществить проверку полученного решения.
· Для пункта задания №3 при поиске максимума и минимума функции построить график заданной функции в заданных границах и отобразить на нем полученные экстремумы маркерами разного цвета.
· Для пункта задания №4 при вычислении интеграла построить график подинтегральной функции, границы графика вводить с клавиатуры и закрасить площадь, ограниченную функцией на заданном отрезке
· Для пункта задания №5 при решении трансцендентного уравнения построить график функции в границах, заданных пользователем в форме диалога, и отобразить на нем значение корня уравнения цветом, отличным от цвета графика.
· На всех графиках должны быть выведены заголовки, названия осей координат. Все графики должны располагаться в одном графическом окне.
При написании программ обязательно:
· использовать комментарии, содержащие назначение программы и описание ее переменных;
· вывод результатов сопровождать пояснительным текстом.
По результатам работы должен быть представлен отчет, содержащий текст индивидуального задания, тексты script -файлов и файлов-функций, а также графическое представление результатов работы.
Варианты индивидуальных заданий
Вариант 1
1. Вычислить корни полинома

2. Найти решение системы линейных уравнений

- Найти значение локального минимума и максимума функции

- Вычислить значение определенного интеграла

- Решить трансцендентное уравнение

Вариант 2
- Вычислить корни полинома

- Найти решение системы линейных уравнений

- Найти значение локального минимума и максимума функции

- Вычислить значение определенного интеграла

- Решить трансцендентное уравнение

Вариант 3
1. Вычислить корни полинома.

2. Найти решение системы линейных уравнений

3. Найти значение локального минимума и максимума функции

4. Вычислить значение определенного интеграла

5. Решить трансцендентное уравнение

Вариант 4
1. Вычислить корни полинома.

2. Найти решение системы линейных уравнений

3. Найти значение локального минимума и максимума функции

4. Вычислить значение определенного интеграла

5. Решить трансцендентное уравнение

Вариант 5
1. Вычислить корни полинома

2. Найти решение системы линейных уравнений

3. Найти значение локального минимума и максимума функции

4. Вычислить значение определенного интеграла

5. Решить трансцендентное уравнение

Вариант 6
1. Найти корни полинома.

2. Найти решение системы линейных уравнений

3. Найти значение локального минимума и максимума функции

4. Вычислить значение определенного интеграла

5. Решить трансцендентное уравнение

Вариант 7
1. Вычислить корни полинома

2. Найти решение системы линейных уравнений

3.  Найти значение локального минимума и максимума функции
Найти значение локального минимума и максимума функции
4. Вычислить значение определенного интеграла

5. Решить трансцендентное уравнение

Вариант 8
1. Вычислить корни полинома

2. Найти решение системы линейных уравнений

3. Найти значение локального минимума и максимума функции

4. Вычислить значение определенного интеграла

5. Решить трансцендентное уравнение

Вариант 9
1. Вычислить корни полинома

2. Найти решение системы линейных уравнений

3. Найти значение локального минимума и максимума функции

4. Вычислить значение определенного интеграла

5. Решить трансцендентное уравнение

Вариант 10
1. Вычислить корни полинома

2. Найти решение системы линейных уравнений

3. Найти значение локального минимума и максимума функции

4. Вычислить значение определенного интеграла

5. Решить трансцендентное уравнение

Лабораторная работа №3
Программирование в системе MAtlab
Цель работы – освоить операторы языка ML, научиться использовать их для решения ситуационных задач.
Постановка задачи – написать скрипт-файл для решения задачи из области математики или физики.
Варианты индивидуальных заданий
Вариант 1
В гелиоцентрической системе отсчета Земля движется по окружности радиуса R1=1.496*108 км (период обращения Т1=3.156*107с). Координаты Земли описываются зависимостями:
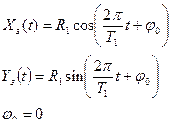
Луна в свою очередь движется вокруг Земли по окружности радиуса R 2 =3.844*105 км (период обращения T2=2.36*106c). Координаты Луны в геоцентрической системе координат :
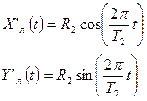
Построить орбиты Земли и Луны в гелиоцентрической системе координат. Промоделировать, как изменится картина при других значениях R 2 и T 2 , например, при R2=3.844*107 км, Т2=2.36*105 с.
Вариант 2
Получить амплитудно-частотную и фазо-частотную характеристики (АЧХ и ФЧХ) цифрового рекурсивного фильтра N -го порядка.
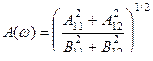 ;
;
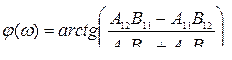 ,
,
где 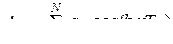 ;
;
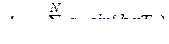 ;
;
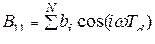 ;
;
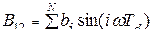 ;
;
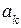 и
и 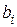 - весовые коэффициенты фильтра,
- весовые коэффициенты фильтра, 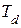 - период дискретизации.
- период дискретизации.
Принять 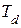 -=0,001с.,N=2,
-=0,001с.,N=2,  -- изменять от 0 до
-- изменять от 0 до 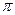 .
.
Значения весовых коэффициентов вводить с клавиатуры:
a0=1; a1=-2,208; a2=1,208; b1=-0,848; b2=0,36
Вариант 3
В ультразвуковом дефектоскопе поисковый элемент (излучатель ультразвуковых импульсов и приемник отраженных сигналов) совершает движение из одного крайнего положения в другое крайнее положение и остановку.
Математическая модель закона изменения ускорения имеет вид:
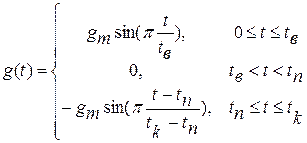
Получить выражения для законов изменения скорости v(t) и пути S(t) и построить зависимости g( t ), v ( t ), S ( t ) для следующих исходных данных:
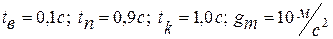
Вариант 4
Построить траекторию спуска космического аппарата в трехмерном пространстве.
Законы изменения составляющих ускорения имеют вид:
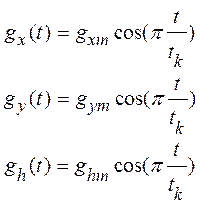
Путем двойного интегрирования получить законы изменения координат x( t ), y ( t ) и h ( t) для следующих начальных условий:
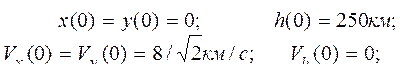
Исходные данные:
gxm=gym= g ;
ghm =-4 g ;
g =9,8 м/с2;
t k =5 мин;
шаг изменения времени ∆t=3c.
Воспользоваться оператором plot 3, местоположение указывать зеленой звездочкой. С помощью операторов line показать проекции точек положения космического аппарата на горизонтальную и вертикальную плоскости.
Вариант 5
Построить траекторию стартующей ракеты в трехмерном пространстве. Законы изменения координат имеют вид:
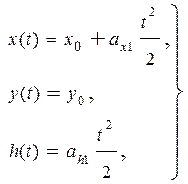 при 0 ≤t≤10
при 0 ≤t≤10

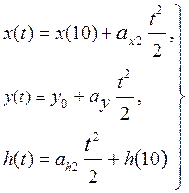 при 10< t ≤50
при 10< t ≤50
где
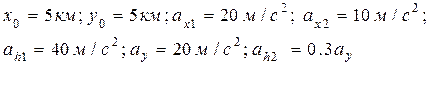
Воспользоваться оператором plot3, местоположение ракеты указывать красной звездочкой. С помощью операторов line показать проекции точек положения летательного аппарата на горизонтальную и вертикальную плоскости. Шаг изменения времени ∆ t =1 c .
Вариант 6
Изобразить интерференционную картину, получившуюся при освещении оранжевым светом с длиной волны l = 0.6 мкм плоской пластины с прижатыми к ней плосковыпуклыми линзами с радиусом кривизны выпуклой поверхности R = 5м.
Разность фаз интерферирующих волн: 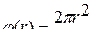 , где
, где
r-расстояние до центра интерференционной картины.
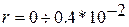 м (шаг изменения
м (шаг изменения 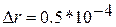 м)
м)
Яркость: 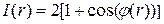
Построить график зависимости I(r) в декартовой и полярной системах координат. Для моделирования интерференционной картины ограничить  м и построить матрицу значений фазы
м и построить матрицу значений фазы 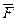 и интенсивности отраженного света
и интенсивности отраженного света 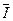 размера 60x60
размера 60x60
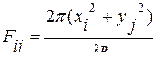
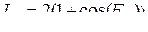
где координаты 
 и
и  изменяются т.о.:
изменяются т.о.:
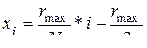 ,
,
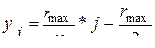 , N=60
, N=60
Построить график зависимости интенсивности отраженного света от координат и карту линий одного уравнения (командой Contour)
Вариант 7
Биоритмы человека представляют собой синусоиды, выходящие из нуля в день рождения человека и имеющие периоды:
· интеллектуальный – 33 дня
· эмоциональный – 28 дней
· физический – 23 дня.
По введенной дате рождения человека построить графики его биоритмов на текущий месяц (или указанный). Выделить на нем текущий день (или указанный).
Вариант 8
Колесо электровоза, движущегося со скоростью 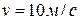 , имеет радиус
, имеет радиус 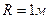 . Необходимо рассчитать и построить траекторию точки, лежащей на расстоянии
. Необходимо рассчитать и построить траекторию точки, лежащей на расстоянии 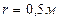 от оси колеса. Считать, что в начальный момент времени точка находилась в самом нижнем положении. Кинематические уравнения движения точки:
от оси колеса. Считать, что в начальный момент времени точка находилась в самом нижнем положении. Кинематические уравнения движения точки:
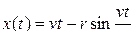
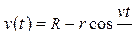
Построить график на интервале 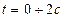 . Указать на графике положения точки в моменты
. Указать на графике положения точки в моменты 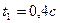 и
и 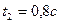 . Изобразить вектора скорости движения точки для моментов
. Изобразить вектора скорости движения точки для моментов 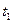 и
и 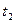 .
.
Вариант 9
Осуществить гармонический синтез пилообразного сигнала по первым 3, 6 и 15 гармоникам
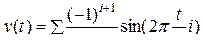
Для этого суммировать 3, 6 и 15 синусоидальных сигналов соответственно. Построить графики полученных сигналов при T = 50, t =0 ÷ T
Вариант 10
В момент преодоления самолетом звукового барьера число Маха становится равным 1. Функция, определяющая число Маха:
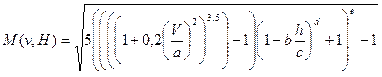
где
v-скорость полета самолета;
H - высота полета;
Коэффициенты:
a=1222,5;
b=6,875*10-6;
c=0,3048;
d=-5,2656;
e=0,286.
Получить графики зависимости M(v) для H=500; 1000; 2000; 5000; показать уровень М=1, соответствующий достижению скорости звука.
Из условия M(v,H)=1 получить зависимость скорости преодоления звукового барьера v от высоты H. Для этого, изменяя H в диапазоне от 0 до 2,5*104, решать уравнение . M(v,H)-1=0. При решении уравнения передавать H в функцию, описывающую правую часть уравнения, как глобальное данное (командой global H). Построить график зависимости v (H), при котором M(v,H)=1
(Для сведения:
при 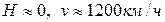 ;
;
при 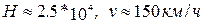 )
)
По результатам работы должен быть представлен отчет, содержащий текст индивидуального задания, тексты script -файлов и файлов-функций, а также графическое представление результатов работы.
Контрольные вопросы.
1. Каково назначение системы MATLAB?
2. В каких режимах может выполняться работа в системе ML?
3. В виде каких файлов хранится большинство команд и функций системы ML?
4. Опишите структуру окна рабочей среды ML.
5. Для чего в ML используют клавиши управления и ¯?
6. Что является элементарной единицей данных языка ML?
7. Как записываются действительные числа в ML ?
8. Какими командами можно получить информацию о данных, хранящихся в рабочем пространстве?
9. Какие форматы вывода числовых данных в ML вы знаете?
10. Как изменить формат вывода результатов вычисления в ML?
11. Как в системе ML определяется тип переменных?
12. Назовите правила составления имен переменных.
13. Какие основные системные переменные существуют в ML?
14. Какие операции существуют в ML?
15. Назовите операции ML в порядке убывания приоритета.
16. Как представляются вектора и матрицы в ML?
17. Как записываются и чем отличаются матричные и поэлементные операции в ML?
18. Назовите способы задания векторов в ML.
19. Как обратиться к элементам векторов и матриц?
20. Для чего используется функция length()?
21. Как обратиться к последнему элементу вектора?
22. Какими командами формируются особые матрицы?
23. Для чего используется символ двоеточие (:), символ точка с запятой (;) и символ многоточие (…)?
24. Для чего используются [], ()?
25. Какие функции используются для обработки векторов и матриц?
26. Какие команды используются для построения графиков функции одной переменной? В чем их различия?
27. Какие команды используются для построения графиков функции двух переменных? В чем их различия?
28. Каков порядок действий для построения графика функции вида y=f(x)?
29. Каков порядок действий для построения графика функции вида z = f ( x , y )?
30. Как построить несколько графиков в одних координатных осях?
31. Как можно управлять внешним видом графика?
32. Каким образом можно вывести несколько графиков в разных координатных осях в одном окне?
33. Какие средства предоставляет система ML для построения диаграмм?
34. Как задается полином?
35. Чему равно число элементов в векторе, определяющем полином?
36. Что такое m-файлы?
37. Какие виды m-файлов вы знаете? Чем они отличаются?
38. Каковы правила записи команд в m-файлах?
39. Как создать m-файл?
40. Как вызывается файл-программа в ML?
41. Какова структура файла-функции в ML?
42. Как вызывается файл-функция в ML?
43. Как описать функцию с несколькими входными и выходными параметрами?
44. Какой командой можно ввести данные с клавиатуры в ML ?
45. Какой командой можно вывести данные на монитор в ML?
46. Какие операторы цикла существуют в ML?
47. Какие операторы используются для организации ветвлений в ML?
48. Для чего используются функции menu и eval?
49. Для чего используются команды break , return и exit?
50. Какие команды используются для организации диалога в ML?
51. Что означает знак %?
52. Почему в системе ML вместо циклов рекомендуется использовать соответствующие векторные и матричные операции?
53. Напишите программу вычисления косинуса 101 значения аргумента от 0 до 10 двумя разными способами.
Библиографический список
1. Hunt, Brian R. Matlab: официальный учебный курс Кембриджского университета. – М.: Триумф, 2008.- 352с.
2. Алексеев Е.Р., Чеснокова О. В. MATLAB 7 (Самоучитель). – М.: NT Press, 2006. – 464с.
3. Курбатова Е. А., Matlab 7, самоучитель.- М.:, Диалектика, 2006. - 256с.
Содержание
Предисловие. 4
Назначение Matlab. 4
Интерфейс Matlab 6.5. 5
Вычисления в ML.. 11
Особенности ввода команд и данных. 11
Элементы данных в ML.. 12
Форматы представления результатов вычислений. 12
Переменные в ML.. 14
Задание векторов и матриц. 16
Способы задания векторов. 16
Задание матриц. 18
Операции в ML.. 19
Приоритет операций в ML.. 22
Элементарные функции. 22
Особые матрицы.. 23
Операции с векторами и матрицами. 26
Выполнение операций с векторами. 26
Выполнение операций над матрицами. 28
Специальные функции для матриц. 33
Действия с элементами матрицы.. 33
Функции, используемые для работы с векторами и матрицами. 39
Действия с полиномами (многочленами) 45
Графика в ML.. 47
Построение простейших графиков. 47
Вывод нескольких графиков в одном окне. 53
Диаграммы.. 55
Построение графиков в полярных координатах. 59
Трехмерная графика. 61
Программирование в ML.. 67
Операторы языка. 68
Операторы ввода/вывода. 69
Операторы цикла и условные операторы. 70
Оператор цикла с предусловием.. 73
Условный оператор. 74
Оператор переключения (выбора) 76
Встроенные функции eval и menu. 77
Создание и использование m-файлов. 79
Script-файлы.. 80
Файлы-функции. 81
Отличия файла-функции от Scipt-файла: 83
Использование файлов- функций. 84
Построение графика. 84
Вычисление интеграла. 85
Решение трансцендентных уравнений. 88
Нахождение минимума функции на заданном отрезке. 89
Решение систем дифференциальных уравнений. 90
Лабораторная работа №1 Знакомство с пакетом Matlab. решение простейших задач в системе Matlab. 93
Лабораторная работа №2 Решение типовых вычислительных задач в системе Matlab 101
Лабораторная работа №3 Программирование в системе Matlab. 109
Контрольные вопросы. 116
Библиографический список. 118
Решение задач в системе Matlab.
Составители: Лазарева Татьяна Ильинична, Мартынова Ирина Владимировна, Ракова Ирина Константиновна .
Редактор Г. М. Звягина
Подписано в печать __.__.2012. Формат 60х84/16.
Бумага документная. Печать трафаретная. Усл. печ. л. ___ .
Уч.-изд. л. 1,5. Тираж 100 экз. Заказ №
Балтийский государственный технический университет
Типография БГТУ
190005, С.-Петербург, 1-я Красноармейская ул., д.1
решение задач в системе matlab
Лабораторный практикум
Государственное Федеральное бюджетное образовательное учреждение
высшего профессионального образования
Балтийский государственный технический университет «Военмех» им. Д.Ф.Устинова
Кафедра информационных систем и компьютерных технологий
Дата: 2019-02-02, просмотров: 2604.