Лекция 1
Задачи линейного программирования транспортного типа.
Транспортная задача и ее модификации.
3.Открытая и Закрытая транспортные модели.
Приведение открытой транспортной модели к замкнутой транспортной модели.
Основы теории определителей и теории матриц.
Понятия минора и алгебраического дополнения. Вычисления определителей. Свойства определителей.



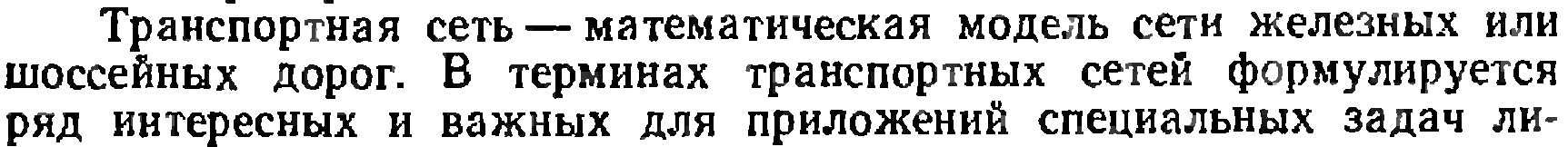





…………………
…………………
………………
……………….


















5.Основные вопросы теории определителей и теории матриц
Рассматрим так же квадратичные формы, виды квадратичных форм и их геометрическая интерпретация.
С появлением ЭВМ стали широко внедряться численные методы не только для научных исследований, но и для решения практических задач в различных отраслях. Начали интенсивно разрабатываться методы решения различных экономических задач. Большое место среди них занимают задачи, которые сводятся к линейным моделям.
К ним относятся задачи линейного программирования, транспортные задачи, матричные игры.
Теоретической базой линейных экономических моделей является линейная алгебра.
Рассматрим основные вопросы теории определителей и теории матриц.
Систем линейных уравнений и методы их решения. Рассматрим так же квадратичные формы, виды квадратичных форм и их геометрическая интерпретация.
ОПРЕДЕЛИТЕЛИ.
Формулировка определителей.
Будем рассматривать конструктивные определения определителей.
Определение 1. Определителем первого порядка называется любое число и обозначается 
Пример. Вычислить определитель

Определение 2. Определителем второго порядка называется число, представленное в виде таблицы, состоящей из двух строк и двух столбцов.
Определитель второго порядка обозначается и вычисляется следующим образом:

Пример. Вычислить определитель

Определение 3. Определителем третьего порядка называется число, представленное в виде таблицы, состоящей из трёх строк и трёх столбцов. Определитель третьего порядка обозначается

Определение 4. Определителем n − го порядка называется число, представленное в виде таблицы, состоящей из n строк и n столбцов. Определитель n − го порядка обозначается

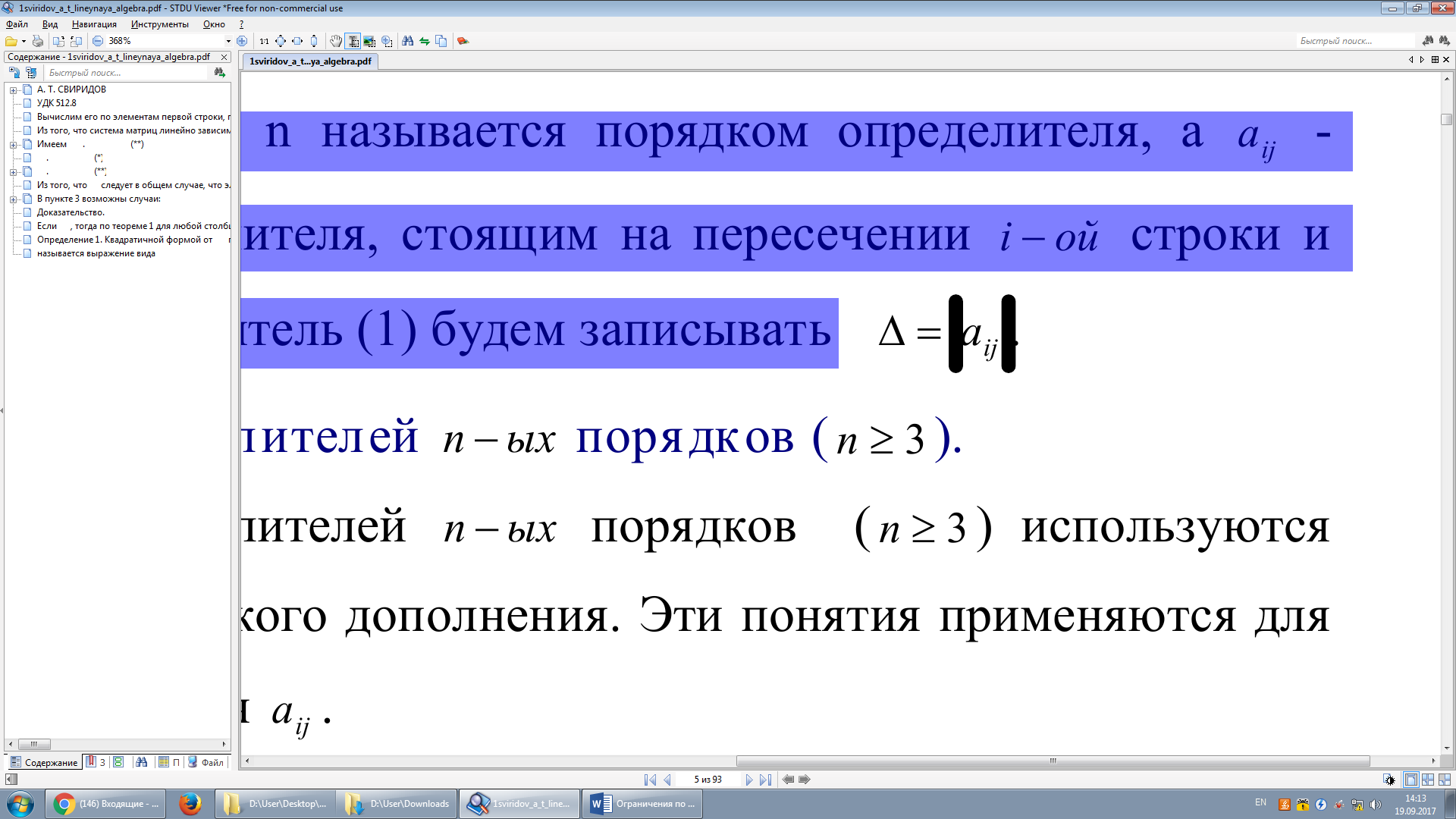
Определение 5. Число n называется порядком определителя, а aij -
называется элементом определителя, стоящим на пересечении i − ой строки и j - го столбца.
Кратко определитель (1) будем записывать
Вычисления определителей n −ых порядков ( n ≥ 3).
Понятие минора
Для вычисления определителей n −ых порядков (n ≥ 3) используются понятия минора и алгебраического дополнения. Эти понятия применяются для каждого элемента определителя аij .
Определение 1. Минором элемента aij называется определитель, который получается из исходного определителя после вычёркивания i − ой строки и j − го столбца. Минор этого элемента обозначается Mij. Из определения следует, что минор есть определитель и его порядок на единицу меньше, чем у исходного определителя.
Пример 1. Записать миноры M12,M31,M23 определителя

Решение

Определение 2. Алгебраическим дополнением элемента aij называется минор этого элемента, взятый со знаком плюс или минус. Плюс берётся тогда, когда сумма индексов (i + j) чётная, а минус - когда нечётная. Алгебраическое дополнение этого элемента обозначается Aij. Из определения можно записать формулу для вычисления алгебраического дополнения

Пример 2. Используя предыдущий пример, вычислить алгебраические дополнения A12 , A31, A23.
Решение. 
Определение 3. Определитель n − го (n ≥ 3) порядка равен сумме произведения элементов, какой – либо строки (или столбца) на соответствующие алгебраические дополнения. Из определения следует, что определитель n − го порядка можно вычислить 2n способами.
Пример 3. Вычислить определитель

Решение.
Свойства определителей.
В приложениях, где используются определители, и для упрощения вычислений, часто используются свойства определителей.
Определение 1. Если в определителе строки заменить столбцами (или наоборот), сохраняя порядок их следования, то такая операция называется транспонированием.
Свойство 1. Величина определителя при его транспонировании не меняется.
Свойство 2. Если в определителе поменять местами две строки (или два столбца), то абсолютная величина его не изменится, а знак поменяется на противоположный.
Свойство 3. Если все элементы какой-либо строки (или столбца) равны нулю, то определитель равен нулю.
Свойство 5. Если элементы какой-либо строки (или столбца) имеют один и тот же множитель, то его можно вынести за знак определителя.
Свойство 6. Определитель с двумя пропорциональными строками (или столбцами) равен нулю.
Свойство 7. Если все элементы строки (или столбца) являются суммами из одинакового числа слагаемых, то определитель равен сумме определителей, в которых элементами этой строки (или столбца) есть отдельные слагаемые.
Свойство 8. Определитель не изменится, если к элементам, какой либо строки (или столбца) прибавить соответствующие элементы другой строки (или столбца), умноженное на одно и то же число k .
Свойство 9. Сумма произведений элементов какой-либо строки (или столбца) определителя на алгебраические дополнения соответствующих элементов параллельной строки (или столбца) равна нулю, т.е.

Литература
1.Абрамов Л.М., Капустин В.Ф. Математическое программирование. Ленинград, ЛГУ, 1976.
КГТУ, 2000.
Лекция 1
Задачи линейного программирования транспортного типа.
Дата: 2019-02-02, просмотров: 737.