ρ = R
3. Определение скорости при естественном способе задания ее движения. (стр 44 –45)
Постановка задачи .
Пусть известны:
1. траектория движения точки АВ.
2. начало отсчета и положительное направление отсчета дуговой координаты s .
3. закон движения по траектории s = s ( t )
Определить скорость точки по модулю и направлению.
Запишем исходную формулу, определяющую вектор скорости.
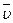 =
= 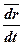 ,
,
Положение точки можно определить с помощью радиуса - вектора 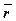 , с другой стороны положение точки определяется с помощью дуговой координаты s.
, с другой стороны положение точки определяется с помощью дуговой координаты s.
Тем самым мы считаем, что радиус вектор есть функция дуговой координаты s , а она зависит от времени t , т. е. радиус - вектор есть сложная функция от времени, выраженная посредством промежуточной величины s .
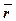 =
= 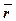 [ s ( t ) ],
[ s ( t ) ],
Продифференцируем сложную функцию, для этого сначала вычислим производную по промежуточной переменной, а потом производную от промежуточной по окончательной переменной.
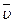 =
= 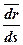
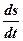 , ( 4»)
, ( 4»)
Как известно
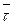 =
= 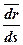 ( 4 )
( 4 )
т.е. если мы вернемся к формулам скорости, то можно записать
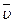 =
= 
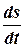
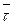 или
или 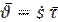 (5)
(5)
Вектор скорости 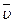 направлен по касательной к траектории
направлен по касательной к траектории
Исследуем этот результат:
Если
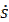 > 0, то
> 0, то 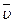 ↓↓
↓↓ 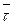
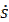 < 0, то
< 0, то 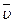 ↓↑
↓↑ 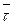
 |
Определим модуль скорости, необходимо продифференцировать закон движения и взять его по модулю.
/ 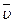 /= /
/= / 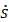
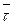 /
/
т.к. | 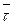 | = 1, т.е. единичный вектор, то
| = 1, т.е. единичный вектор, то
/ 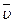 /=
/=  /
/ 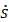 / ( 6 )
/ ( 6 )
Найдем проекцию вектора скорости на касательную
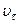 =
= 
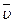
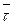
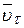 - проекция вектора скорости на касательную
- проекция вектора скорости на касательную
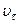 =
= 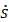
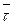
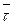 =
= 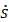
Опять возвращаемся к математике.
Положительное направление оси можно определить единичным вектором.
Запишем проекцию любого вектора на любую ось:
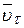 =
= 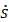
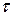 cos (
cos ( 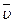
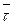 )
)
cos 0 = 1
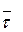 2 = 12 = 1
2 = 12 = 1
окончательно
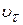 =
= 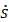 (7)
(7)
Сравним формулы (3) и (4). Эти величины могут отличаться знаком. Договоримся обозначать 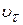 через
через 
 =
= 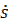 (8)
(8)
Скорость, определенная формулой (6) называется алгебраической скоростью точки, а знак может быть больше, меньше или равна нулю.
Если
 >0, то точка движется в сторону возрастания дуговой координаты
>0, то точка движется в сторону возрастания дуговой координаты
 <0 то точка движется в сторону убывания дуговой координаты
<0 то точка движется в сторону убывания дуговой координаты
Эти величины могут отличаться только знаком, алгебраическое значение у них одинаковое.
Договоримся и модуль скорости, и его проекцию обозначать буквой  .
.
Окончательно:
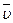 =
= 
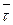
 =
= 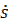
Пример
Пусть
s = 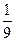 t 2 -
t 2 - 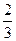 t
t
Определить направление движения точки
 =
= 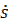 =
= 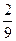 t -
t - 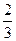 =
= 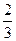 (
( 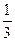 t -1 )
t -1 )
Знак скорости определяется знаком скобки:
если 0 < t < 3, то скорость  <0 ,
<0 ,
при t = 3  =0, т.е. в данный момент точка остановилась,
=0, т.е. в данный момент точка остановилась,
если t > 3, то  >0 , то точка движется в сторону возрастания дуговой координаты.
>0 , то точка движется в сторону возрастания дуговой координаты.
Для того, чтобы ввести понятие ускорения точки в естественной форме нам необходимы знания высшей математики.
4. Определение ускорения при естественном способе задания ее движения. (стр 51-54)
Постановка задачи .
Пусть известны:
1. траектория движения точки АВ.
2. начало отсчета и положительное направление отсчета дуговой координаты s .
3. закон движения по траектории s = s ( t )
Определить ускорение точки по модулю и направлению.
Запишем исходные формулы ускорения и скорости:
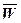 =
= 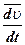
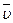 =
= 
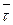 ,
,
где  алгебраическая скорость точки , а
алгебраическая скорость точки , а 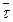 единичный орт.
единичный орт.
Подставим в первую формулу вектор скорости, т. е продифференцируем данное произведение. Необходимо учесть, что скорость меняется (движение может быть неравномерным), а вектор 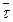 модуль которого равняется единице переменный по направлению, но постоянный по значению. Поэтому придется продифференцировать оба множителя. Дифференцируем как произведение.
модуль которого равняется единице переменный по направлению, но постоянный по значению. Поэтому придется продифференцировать оба множителя. Дифференцируем как произведение.
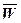 =
= 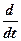 (
( 
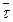 )
)
Дифференцируем как произведение.
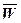 =
= 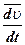
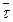 +
+ 
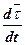 (9)
(9)
Вектор 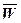 мы представили в виде двух составляющих.
мы представили в виде двух составляющих.
Вектор 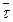 - показывает, что первое слагаемое направлено по касательной, а второй вектор показывает направление по нормали.
- показывает, что первое слагаемое направлено по касательной, а второй вектор показывает направление по нормали.
Дальше необходимы знания дифференциальной геометрии. Необходимо рассмотреть формулы ФРЭНЕ.
Запишем формулу без вывода.
Можно доказать следующее выражение:
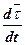 =
= 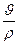
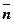
И тогда ускорение можно записать:
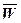 =
= 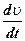
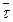 +
+ 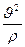
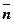 (10)
(10)
Данная формула показывает разложение вектора ускорения по естественным осям координат.
Введем следующие обозначения:
Wτ = 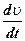 - касательная составляющая ускорения
- касательная составляющая ускорения
Wn = 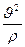 - нормальная составляющая ускорения
- нормальная составляющая ускорения
Wb = 0 - составляющая по бинормали
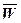 =
= 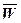 τ +
τ + 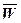 n (11)
n (11)
Дата: 2019-02-02, просмотров: 285.