Dr ( dx, dy, dz)
Тогда модуль dr будет равен:
| d 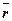 |
|  =
= 
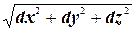 = | ds |
= | ds |
Каков смысл этого корня? Что он показывает с точки зрения геометрии?
С точки зрения геометрии | ds |- этот радикал определяет элемент дуги равный по абсолютному значению ds . Или этот радикал определяет, что криволинейную дугу s мы заменили прямолинейной ds . Это значение приближенное с точностью до величин второго порядка.(высшего порядка малости)
Тогда модуль этого вектора
/ 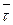 / = /
/ = / 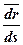 / = 1
/ = 1
Вектор 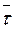 называется единичным вектором или ортом касательной к кривой АВ в точке М.
называется единичным вектором или ортом касательной к кривой АВ в точке М.
Направление 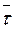
Покажем, что вектор 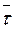 всегда направлен по касательной к траектории в сторону возрастания дуговой координаты.
всегда направлен по касательной к траектории в сторону возрастания дуговой координаты.
Сравним направления вектора d 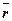 и
и 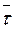
Изобразим два рисунка.
Первый рисунок.
Изображаем траекторию «а в», На этой траектории выберем точку О' начало отсчета дуговой координаты и положительное направление этой дуговой координаты.
Положение точки М на данной траектории будет определяться при помощи дуговой координаты s. Выберем близлежащую к ней точку М1. Перемещение точки М к М1 , обозначим через d 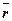 маленькая дуга ds Изобразим орт
маленькая дуга ds Изобразим орт 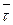 по касательной к траектории.
по касательной к траектории.
 |
d 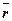 - это вектор элементарного перемещения точки за бесконечно малый промежуток времени dt.
- это вектор элементарного перемещения точки за бесконечно малый промежуток времени dt.
Он всегда направлен по касательной в сторону движения точки и абсолютно не важно в каком направлении точка движется.( в сторону увеличения или убывания дуговой координаты).
Записи будем делать под одной и другой картинкой
| При движении в положительном направлении, когда дуговая координата s возрастает. ( ds > 0 ) | При движении в отрицательном направлении, когда дуговая координата s убывает. ( ds < 0 ) |
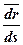 ↓↓ d ↓↓ d 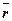 или
или
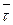 ↓↓ d ↓↓ d 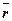
| 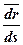 ↓↑ d ↓↑ d 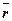 или
или
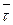 ↓↑ d ↓↑ d 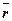
|
Второй рисунок.
 Изображаем траекторию «а в», На этой траектории выберем точку О' начало отсчета дуговой координаты и положительное направление этой дуговой координаты.
Изображаем траекторию «а в», На этой траектории выберем точку О' начало отсчета дуговой координаты и положительное направление этой дуговой координаты.
Положение точки М на данной траектории будет определяться при помощи дуговой координаты s. Выберем близлежащую к ней точку М1, но изобразим ее в противоположном направлении. Перемещение точки М к М1 , обозначим через d 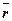 маленькая дуга ds. Изобразим орт
маленькая дуга ds. Изобразим орт 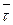 по касательной к траектории. В этом случае ds < 0.
по касательной к траектории. В этом случае ds < 0.
Вывод
Вектор 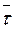 - всегда направлен по касательной к траектории в сторону возрастания дуговой координаты s .
- всегда направлен по касательной к траектории в сторону возрастания дуговой координаты s .
Рассмотрим некоторую пространственную линию. На этой линии возьмем две близкие друг к другу точки М и М1 и построим в этих точках орты касательных 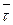 и
и 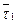 .
.
По модулю они одинаковые, но у нас кривая линия, поэтому направлены они будут по разному.
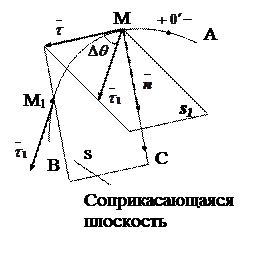 |
Вектор 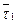 перенесем параллельно самому себе в точку М .
перенесем параллельно самому себе в точку М .
Произведем следующее построение: через 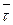 и
и 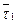 проведем плоскость s1
проведем плоскость s1
Вектор 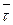 при этом будет менять свою ориентацию в пространстве.
при этом будет менять свою ориентацию в пространстве.
Плоскость s1 будет как-то поворачиваться вокруг вектора 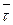 . Пока не займет некоторое предельное положение.
. Пока не займет некоторое предельное положение.
При М → М1 вдоль АВ плоскость будет поворачиваться вокруг вектора 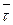 пока не займет предельное положение плоскости s 1 .
пока не займет предельное положение плоскости s 1 .
Изобразим эту плоскость красным мелом.
Плоскость S называется соприкасающейся плоскостью в точке М к АВ.
Любой перпендикуляр к касательной называется нормалью.
Если
 >0, то точка движется в сторону возрастания дуговой координаты
>0, то точка движется в сторону возрастания дуговой координаты
 <0 то точка движется в сторону убывания дуговой координаты
<0 то точка движется в сторону убывания дуговой координаты
Эти величины могут отличаться только знаком, алгебраическое значение у них одинаковое.
Договоримся и модуль скорости, и его проекцию обозначать буквой  .
.
Окончательно:
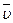 =
= 
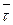
 =
= 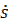
Пример
Пусть
s = 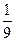 t 2 -
t 2 - 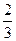 t
t
Определить направление движения точки
 =
= 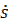 =
= 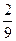 t -
t - 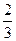 =
= 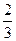 (
( 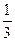 t -1 )
t -1 )
Знак скорости определяется знаком скобки:
если 0 < t < 3, то скорость  <0 ,
<0 ,
при t = 3  =0, т.е. в данный момент точка остановилась,
=0, т.е. в данный момент точка остановилась,
если t > 3, то  >0 , то точка движется в сторону возрастания дуговой координаты.
>0 , то точка движется в сторону возрастания дуговой координаты.
Для того, чтобы ввести понятие ускорения точки в естественной форме нам необходимы знания высшей математики.
4. Определение ускорения при естественном способе задания ее движения. (стр 51-54)
Постановка задачи .
Пусть известны:
1. траектория движения точки АВ.
2. начало отсчета и положительное направление отсчета дуговой координаты s .
3. закон движения по траектории s = s ( t )
Определить ускорение точки по модулю и направлению.
Запишем исходные формулы ускорения и скорости:
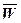 =
= 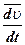
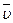 =
= 
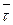 ,
,
где  алгебраическая скорость точки , а
алгебраическая скорость точки , а 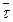 единичный орт.
единичный орт.
Подставим в первую формулу вектор скорости, т. е продифференцируем данное произведение. Необходимо учесть, что скорость меняется (движение может быть неравномерным), а вектор 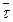 модуль которого равняется единице переменный по направлению, но постоянный по значению. Поэтому придется продифференцировать оба множителя. Дифференцируем как произведение.
модуль которого равняется единице переменный по направлению, но постоянный по значению. Поэтому придется продифференцировать оба множителя. Дифференцируем как произведение.
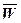 =
= 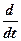 (
( 
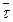 )
)
Дифференцируем как произведение.
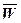 =
= 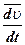
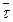 +
+ 
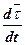 (9)
(9)
Вектор 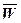 мы представили в виде двух составляющих.
мы представили в виде двух составляющих.
Вектор 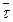 - показывает, что первое слагаемое направлено по касательной, а второй вектор показывает направление по нормали.
- показывает, что первое слагаемое направлено по касательной, а второй вектор показывает направление по нормали.
Дальше необходимы знания дифференциальной геометрии. Необходимо рассмотреть формулы ФРЭНЕ.
Запишем формулу без вывода.
Можно доказать следующее выражение:
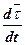 =
= 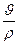
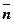
И тогда ускорение можно записать:
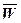 =
= 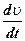
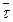 +
+ 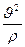
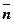 (10)
(10)
Данная формула показывает разложение вектора ускорения по естественным осям координат.
Введем следующие обозначения:
Wτ = 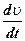 - касательная составляющая ускорения
- касательная составляющая ускорения
Wn = 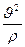 - нормальная составляющая ускорения
- нормальная составляющая ускорения
Wb = 0 - составляющая по бинормали
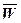 =
= 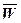 τ +
τ + 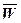 n (11)
n (11)
Dr ( dx, dy, dz)
Тогда модуль dr будет равен:
| d 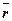 |
|  =
= 
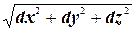 = | ds |
= | ds |
Каков смысл этого корня? Что он показывает с точки зрения геометрии?
С точки зрения геометрии | ds |- этот радикал определяет элемент дуги равный по абсолютному значению ds . Или этот радикал определяет, что криволинейную дугу s мы заменили прямолинейной ds . Это значение приближенное с точностью до величин второго порядка.(высшего порядка малости)
Тогда модуль этого вектора
/ 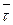 / = /
/ = / 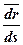 / = 1
/ = 1
Вектор 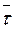 называется единичным вектором или ортом касательной к кривой АВ в точке М.
называется единичным вектором или ортом касательной к кривой АВ в точке М.
Направление 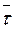
Покажем, что вектор 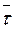 всегда направлен по касательной к траектории в сторону возрастания дуговой координаты.
всегда направлен по касательной к траектории в сторону возрастания дуговой координаты.
Сравним направления вектора d 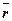 и
и 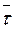
Изобразим два рисунка.
Первый рисунок.
Изображаем траекторию «а в», На этой траектории выберем точку О' начало отсчета дуговой координаты и положительное направление этой дуговой координаты.
Положение точки М на данной траектории будет определяться при помощи дуговой координаты s. Выберем близлежащую к ней точку М1. Перемещение точки М к М1 , обозначим через d 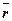 маленькая дуга ds Изобразим орт
маленькая дуга ds Изобразим орт 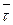 по касательной к траектории.
по касательной к траектории.
 |
d 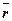 - это вектор элементарного перемещения точки за бесконечно малый промежуток времени dt.
- это вектор элементарного перемещения точки за бесконечно малый промежуток времени dt.
Он всегда направлен по касательной в сторону движения точки и абсолютно не важно в каком направлении точка движется.( в сторону увеличения или убывания дуговой координаты).
Записи будем делать под одной и другой картинкой
| При движении в положительном направлении, когда дуговая координата s возрастает. ( ds > 0 ) | При движении в отрицательном направлении, когда дуговая координата s убывает. ( ds < 0 ) |
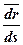 ↓↓ d ↓↓ d 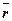 или
или
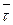 ↓↓ d ↓↓ d 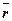
| 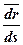 ↓↑ d ↓↑ d 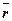 или
или
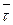 ↓↑ d ↓↑ d 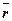
|
Второй рисунок.
 Изображаем траекторию «а в», На этой траектории выберем точку О' начало отсчета дуговой координаты и положительное направление этой дуговой координаты.
Изображаем траекторию «а в», На этой траектории выберем точку О' начало отсчета дуговой координаты и положительное направление этой дуговой координаты.
Положение точки М на данной траектории будет определяться при помощи дуговой координаты s. Выберем близлежащую к ней точку М1, но изобразим ее в противоположном направлении. Перемещение точки М к М1 , обозначим через d 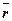 маленькая дуга ds. Изобразим орт
маленькая дуга ds. Изобразим орт 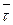 по касательной к траектории. В этом случае ds < 0.
по касательной к траектории. В этом случае ds < 0.
Вывод
Вектор 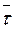 - всегда направлен по касательной к траектории в сторону возрастания дуговой координаты s .
- всегда направлен по касательной к траектории в сторону возрастания дуговой координаты s .
Рассмотрим некоторую пространственную линию. На этой линии возьмем две близкие друг к другу точки М и М1 и построим в этих точках орты касательных 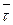 и
и 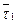 .
.
По модулю они одинаковые, но у нас кривая линия, поэтому направлены они будут по разному.
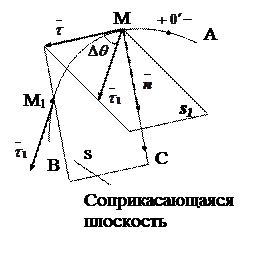 |
Вектор 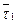 перенесем параллельно самому себе в точку М .
перенесем параллельно самому себе в точку М .
Произведем следующее построение: через 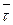 и
и 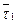 проведем плоскость s1
проведем плоскость s1
Вектор 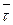 при этом будет менять свою ориентацию в пространстве.
при этом будет менять свою ориентацию в пространстве.
Плоскость s1 будет как-то поворачиваться вокруг вектора 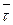 . Пока не займет некоторое предельное положение.
. Пока не займет некоторое предельное положение.
При М → М1 вдоль АВ плоскость будет поворачиваться вокруг вектора 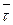 пока не займет предельное положение плоскости s 1 .
пока не займет предельное положение плоскости s 1 .
Изобразим эту плоскость красным мелом.
Плоскость S называется соприкасающейся плоскостью в точке М к АВ.
Любой перпендикуляр к касательной называется нормалью.
Плоскость, содержащая все нормали, называется нормальной плоскостью.
Дата: 2019-02-02, просмотров: 309.