Эти системы заводнения предназначены для разработки крупных НГМ, нефтяные части которых вследствие их значительных размеров нецелесообразно разрабатывать только путём барьерного заводнения (рис 2.3.2).
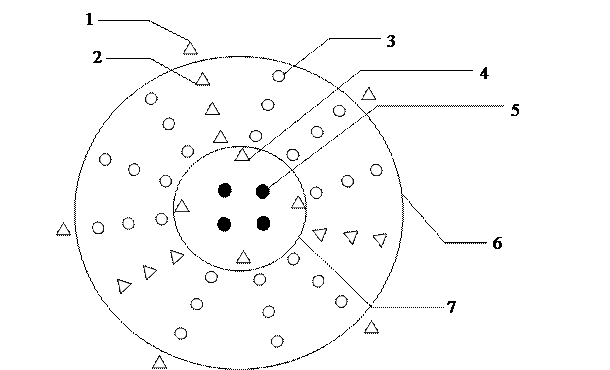
Рис. 2.3.2
Система разработки НГМ с сочетанием барьерного, законтурного и внутриконтурного заводнения
1 – нагнетательные скважины законтурного заводнения;
2 – нагнетательные скважины внутриконтурного заводнения;
3 – нефтедобывающие скважины;
4 – нагнетательные скважины барьерного заводнения;
5 – газодобывающие скважины;
6 – внешний контур нефтеносности;
7 – контур газоносности.
Нефтяная часть месторождения имеет большую ширину, позволяющую разместить несколько полос трёхрядной системы разработки с расстоянием между скважинами 500 – 600 м. Так же как и в предыдущем случае скважины барьерного заводнения отделяют газовую часть от нефтенасыщенной, что способствует осуществлению их более независимой разработке с ограничением перемещения газа в нефтенасыщенную часть пласта.
В некоторых случаях с целью дальнейшего снижения прорыва газа к нефтяным скважинам бурят два барьерных ряда нагнетательных скважин, что приводит к ещё большему снижению газового фактора нефтяных скважин.
ЛЕКЦИЯ 4
6.1. Многофазная фильтрация, непоршневое вытеснение.
Основные характеристики многофазной фильтрации.
Добыча нефти как при естественных режимах эксплуатации, так и при поддержании пластового давления заводнением или нагнетанием газа, происходит посредством замещения нефти в поровом пространстве водой или газом.
При взаимодействии пластовых флюидов между собой со скелетом пористой среды возникают капиллярные явления, неполное и неравномерное вытеснение нефти, образование в продуктивном пласте зон совместного течения флюидов, т.е. многофазной фильтрации. Неполное вытеснение снижает коэффициент нефтегазоотдачи пласта.
Главными характеристиками движения многофазной системы являются насыщенности и скорости фильтрации каждой фазы.
Насыщенность I-фазы определяется отношением
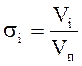
I=1,2,3 (6.1)
где 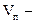 объем порового пространства,
объем порового пространства,
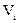 -часть объема порового пространства, занятого I-фазой.
-часть объема порового пространства, занятого I-фазой.
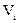
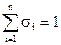 (6.2)
(6.2)
Из (6.2) следует , что в многофазной системе существует n-1 независимых насыщенностей.
Для двухфазных систем (вытеснение нефти водой) в качестве независимой переменной выбирают насыщенность вытесняющей фазы – водонасыщенность.
6.2. Уравнения движения трехфазной фильтрации.
Уравнения движения I-фазы – фильтрации – можно описать законом Дарси, записанным для каждой фазы
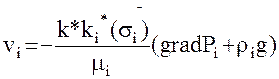 (6.3)
(6.3)
I=1,2,3
где vi – скорость фильтрации I-фазы;
k –абсолютная проницаемость;
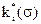
 - относительная проницаемость I- фазы;
- относительная проницаемость I- фазы;
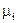 - динамическая вязкость I- фазы;
- динамическая вязкость I- фазы;
Pi- пластовое давление I-фазы;
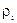 - плотность I-фазы.
- плотность I-фазы.
Давления в фазах вообще говоря не равны между собой и отличаются на величину капиллярного давления.
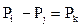 (6.4)
(6.4)
где Pk – капиллярное давление или капиллярный скачок.
Из курса физики пласта известно, что
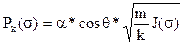 (6.5)
(6.5)
где 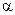 - коэффициент поверхностного натяжения;
- коэффициент поверхностного натяжения;
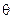 - статический краевой угол смачивания между жидкостями и породой;
- статический краевой угол смачивания между жидкостями и породой;
m- пористость;
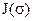 - безразмерная функция Леверетта, которая определяется для каждого типа коллектора.
- безразмерная функция Леверетта, которая определяется для каждого типа коллектора.
6.3 Уравнения неразрывности трех- и двухфазной фильтрации.
Из курса Механики сплошной среды известно, что уравнения неразрывности ( сплошности) можно представить в виде
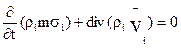 I=1,2,3 (6.6)
I=1,2,3 (6.6)
Обозначения те же.
Для слабосжимаемых или несжимаемых жидкостей, в случае двухфазной фильтрации, имеем
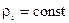
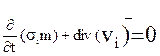 I=1,2 (6.7)
I=1,2 (6.7)
Для непоршневого вытеснения нефти водой, учитывая что 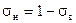
,уравнения (6.7) примут вид
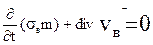
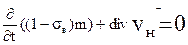 (6.8)
(6.8)
Наиболее разработаны модели одномерного движения двухфазных жидкостей – прямолинейно-параллельное и плоскорадиальное течения.
Одномерные модели предполагают следующие допущения:
- жидкости несжимаемые и несмешиваемые;
- фазовые переходы отсутствуют;
- динамические вязкости 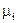 -постоянны;
-постоянны;
- относительные проницаемости и капиллярное давления являются известными функциями водонасыщенности;
- пористая среда несжимаема m- const.
при этих предположениях, полагая 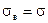 из (6.8) получим
из (6.8) получим
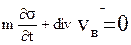

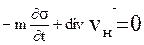 (6.9)
(6.9)
Суммируя уравнения (6.9), получим
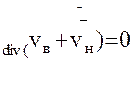 (6.10)
(6.10)
Поскольку 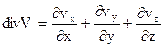 , из (6.10) следует , что суммарная скорость фильтрации двух фаз не зависит от координат, а зависит только от времени
, из (6.10) следует , что суммарная скорость фильтрации двух фаз не зависит от координат, а зависит только от времени
v(t)=vв(t)+vн(t) (6.11)
Из (6.11) следует, что суммарный объемный расход для прямолинейно-параллельного потока также зависит только от времени или может быть постоянным:
Q(t)=v(t)Bh (6.12)
где B,h – ширина и толщина галереи(пласта)
Для плоскорадиального потока объемный расход(дебит) зависит от времени и от r –расстояния до оси скважины;
Q(t)=v(t)2 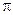 rh (6.13)
rh (6.13)
Полная система уравнений для описания двухфазной фильтрации состоит из 4-х уравнений движения (6.3), двух уравнений неразрывности (6.9), которые дополняются уравнениями состояния или реологическими уравнениями, начальными и граничными условиями.
6.4 Уравнение для определения насыщенности.
Рассмотрим прямолинейно-параллельное вытеснение нефти водой
Рис.6.1
Рис. 6.1. Схема одномерной двухфазной фильтрации с учетом сил тяжести.
Капиллярное давление считаем известной функцией насыщенности
Pн=Pв+Pk( 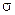 ) (6.4)
) (6.4)
Уравнения фильтрации (6.3) для наклонного пласта примут вид:
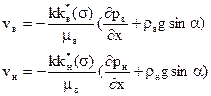 (6.14)
(6.14)
Решаем (6.14) с учетом (6.4) и (6.11) .Введем функцию Бакли-Леверетта
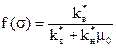 (6.15)
(6.15)
где 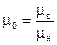 . Обозначим
. Обозначим 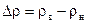
тогда выражение для скорости фильтрации воды примет вид
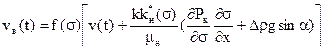 (6.16)
(6.16)
введем безразмерные координаты 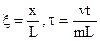 где L- длина пласта.
где L- длина пласта.
Пусть суммарная скорость фильтрации v= const
Подставим (6.16) в уравнение неразрывности (6.9), тогда с учетом (6.5) после преобразований, получим уравнение для определения насыщенности
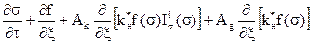 (6.17)
(6.17)
Здесь Ag , Ak –безразмерные параметры, характеризующие отношения сил тяжести и капиллярных сил к силам вязкости и равны
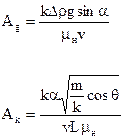 (6.18)
(6.18)
Параметр Ak =0, если рассматривать вытеснение в пласте где L – велико, или если пренебречь капиллярными силами.
Если 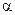 мало, то силами тяжести также можно пренебречь, Ag=0.
мало, то силами тяжести также можно пренебречь, Ag=0.
6.5. Модель Бакли-Леверетта непоршневого вытеснения нефти водой
В этой модели капиллярными и массовыми силами пренебрегают Ak=Ag=0
Тогда уравнение (6.17) примет вид
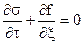 или
или 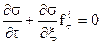 (6.19)
(6.19)
где f( 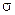 )=
)= 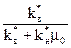 функция Бакли-Леверетта или функция распределения потока фаз,
функция Бакли-Леверетта или функция распределения потока фаз, 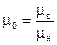
В координатах t,x (6.19) примет вид
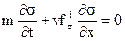 (6.20)
(6.20)
Из выражения (6.16) и (6.11) следует что
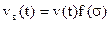
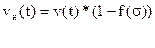
Таким образом, функция Бакли-Леверетта равна объемной доле потока вытесняющей жидкости в суммарном потоке двух фаз.
Поскольку суммарная скорость не зависит от x и плотность жидкостей константа, то режим жесткий, упруговодонапорный.
По мере продвижения воды в прямолинейном пласте фронт воды продвигается к галереи нефтедобывающих скважин, водонасыщенность 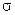 в каждом сечении заводненной области увеличивается. В какой-то момент времени t насыщенность будет равна
в каждом сечении заводненной области увеличивается. В какой-то момент времени t насыщенность будет равна 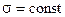 , через некоторое время это же значение будет и в конце пласта на забоях добывающих скважин. Поэтому
, через некоторое время это же значение будет и в конце пласта на забоях добывающих скважин. Поэтому
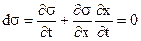 (6.21)
(6.21)
Сравнивая (6.20) и (6.21) для v- постоянной, из уравнения материального баланса получим зависимость для 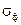 - насыщенности на фронте вытеснения
- насыщенности на фронте вытеснения
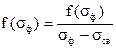 (6.22)
(6.22)
где 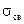 - остаточная связанная вода.
- остаточная связанная вода.
Время безводного периода определяется
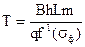 (6.23)
(6.23)
Учитывая, что режим жесткий водонапорный объем закаченной воды будет равен объему добываемой жидкости, и коэффициент вытеснения нефти водой будет равен с учетом (6.23)
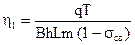 =
= 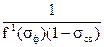 (6.24)
(6.24)
КИН равен
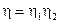 (6.25)
(6.25)
где 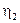 - коэффициент охвата пласта заводнением. Для определения КИН безводного периода (6.24) подставляем в (6.25).
- коэффициент охвата пласта заводнением. Для определения КИН безводного периода (6.24) подставляем в (6.25).
Добыча нефти продолжается и после достижения фронта вытеснения галереи добывающих скважин. Текущая обводненность определится как
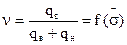 (6.26)
(6.26)
где 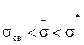 ,
, 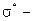 предельное значение водонасыщенности.
предельное значение водонасыщенности.
Время 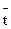 ,соответствующее
,соответствующее 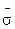 , определяется из соотношения
, определяется из соотношения

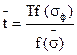 (6.27)
(6.27)
Значения 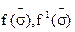 определяются из соответствующих графиков.
определяются из соответствующих графиков.
Коэффициент извлечения нефти в период водной эксплуатации определяется
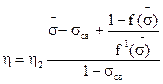 (6.28).
(6.28).
Дата: 2019-02-02, просмотров: 493.