Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

ИНЖЕНЕРНАЯ ГЕОДЕЗИЯ

 

Учебное пособие

 

 

Часть I

 

 

САНКТ-ПЕТЕРБУРГ

2006

УДК 528.48

 

 

Инженерная геодезия. Учебное пособие, часть I / Е.С. Богомолова, М.Я. Брынь, В.В. Грузинов, В.А. Коугия, В.И. Полетаев; под ред. В.А. Коугия. – СПб.: Петербургский гос. ун-т путей сообщения, 2006. - с.

 

 

Изложены предмет и задачи инженерной геодезии, сведения о системах координат и высот, методах построения плановых и высотных геодезических сетей, элементы теории погрешностей измерений, приборы и методы, применяемые для измерения углов и расстояний, приборы и методы нивелирования.

Разделы 1, 6 пособия написаны М.Я. Брынем, 2, 9 – Е.С. Богомоловой, 3 – В.В. Грузиновым, 4, 8 – В.А. Коугия, 5, 7 – В. И. Полетаевым.

Предназначено для студентов, обучающихся по железнодорожным и строительным специальностям.

 

ПРЕДМЕТ ИНЖЕНЕРНОЙ ГЕОДЕЗИИ

Геодезия – наука, изучающая фигуру и внешнее гравитационное поле Земли и разрабатывающая методы создания систем координат, определения положения точек на Земле и околоземном пространстве, изображения земной поверхности на картах.

Научными задачами геодезии являются:

- установление систем координат;

- определение формы и размеров Земли и ее внешнего гравитационного поля и их изменений во времени;

- проведение геодинамических исследований (определение горизонтальных и вертикальных деформаций земной коры, движений земных полюсов, перемещений береговых линий морей и океанов и др.).

Научно-технические задачи геодезии в обобщенном виде заключаются в следующем:

- определение положения точек в выбранной системе координат;

- составление карт и планов местности разного назначения;

- обеспечение топографо-геодезическими данными нужд обороны страны;

- выполнение геодезических измерений для целей проектирования и строительства, землепользования, кадастра, исследования природных ресурсов и др. 

Геодезия в процессе своего развития разделилась на ряд научных дисциплин: высшую геодезию, топографию, фотограмметрию, картографию, космическую геодезию, морскую геодезию, инженерную геодезию.

Особое место в этом ряду занимает инженерная геодезия, которая разрабатывает методы геодезического обеспечения изысканий, проектирования, строительства и эксплуатации инженерных сооружений: железных и автомобильных дорог, мостов, тоннелей, трубопроводов, промышленных и гражданских зданий, систем водоснабжения и водоотведения и др.

Основными задачами инженерной геодезии являются:

- топографо-геодезические изыскания, в ходе которых выполняется создание на объекте работ геодезической сети, топографическая съемка, геодезическая привязка точек геологической и геофизической разведки;

- инженерно-геодезическое проектирование, включающее разработку генеральных планов сооружений и их цифровых моделей; геодезическую подготовку проекта для вынесения его в натуру, расчеты по горизонтальной и вертикальной планировке, определению площадей, объемов земляных работ и др.;

- геодезические разбивочные работы, включающие создание на объекте геодезической разбивочной сети и последующий вынос в натуру главных осей сооружения и его детальную разбивку;

- геодезическая выверка конструкций и технологического оборудования при установке их в проектное положение;

- наблюдения за деформациями сооружений, определяющие осадки оснований и фундаментов, плановые смещения и крены сооружений.

Геодезическое обеспечение строительства и эксплуатации современных инженерных сооружений связано с необходимостью выполнения точных измерений, служащих определению координат и высот геодезических пунктов, составлению топографических карт и планов, продольных профилей трасс; наблюдению за деформациями сооружений. Для обеспечения необходимой точности измерения выполняются высокоточными геодезическими приборами: теодолитами – угловые измерения; светодальномерами – линейные измерения; электронными тахеометрами – угловые и линейные измерения с решением различных инженерно-геодезических задач; нивелирами – определение превышений. При определении положения объектов используется аппаратура, работающая по сигналам спутниковых навигационных систем, при выполнении топографической съемки местности находят применение лазерные сканеры. Обработка результатов геодезических измерений выполняется на современных компьютерах с использованием развитого программного обеспечения. К числу таких программных продуктов относятся геоинформационные системы, служащие сбору, обработке, систематизации, отображению и анализу картографической информации.

Состав геодезических работ, их точность, используемые методы и приборы различаются в зависимости от особенностей объекта.

Так, при выполнении изысканий железной дороги создают геодезическую сеть, опираясь на которую составляют топографические карты и планы. На картах и планах выполняют предварительное трассирование дороги, окончательное положение которой выбирают в поле. Затем делают съемку трассы и получают необходимые для проектирования дороги профиль трассы и ситуационный план полосы местности.

Для обеспечения безопасного движения поездов вдоль железной дороги создают высокоточную геодезическую сеть (так называемую, реперную систему), опираясь на которую выполняют работы по реконструкции и ремонту пути, по оперативному контролю его геометрических параметров, по наблюдениям за деформациями пути, земляного полотна и искусственных сооружений.

В процессе строительства и по мере завершения отдельных его этапов выполняются исполнительные съемки, целью которых является установление точности вынесения проекта сооружения в натуру, выявление отклонений, допущенных в процессе строительства, а также определение фактических координат и высотных отметок построенных объектов, размеров его отдельных частей.

 

ВЫСОТЫ

 

Форма и размеры Земли

Изучение формы и размеров Земли включает решение двух задач. Это - установление некоторой сглаженной, обобщенной, теоретической фигуры Земли и определение отклонений от нее фактической физической поверхности.

Учитывая, что поверхность океанов и морей составляет 71% поверхности Земли, а поверхность суши - только 29%, за теоретическую фигуру Земли принято тело, ограниченное поверхностью океанов в их спокойном состоянии, продолженной и под материками, и называемое геоидом.

Поверхность, в каждой своей точке перпендикулярная к отвесной линии (направлению силы тяжести), называется уровенной поверхностью. Из множества уpовенных поверхностей одна совпадает с поверхностью геоида.

Из-за неравномерности распределения масс в земной коре геоид имеет неправильную геометрическую форму, и его поверхность нельзя выразить математически, что необходимо для решения геодезических задач. При решении геодезических задач геоид заменяют близкими к нему геометрически правильными поверхностями.

Так, для приближенных вычислений Землю принимают за шар с радиусом 6371 км.

Ближе к форме геоида подходит эллипсоид – фигура, получаемая вращением эллипса (рис. 2.1) вокруг его малой оси. Размеры земного эллипсоида характеризуют следующими основными параметрами: a - большая полуось, b - малая полуось, a - полярное сжатие и e – первый эксцентриситет меридианного эллипса, где 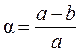 и .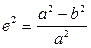

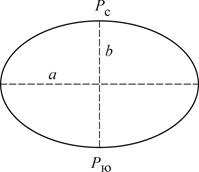
Рис. 2.1. Меридианный эллипс: Рс – северный полюс; Рю – южный полюс

 

Различают общеземной эллипсоид и референц-эллипсоид.

Центр общеземного эллипсоида помещают в центре масс Земли, ось вращения совмещают со средней осью вращения Земли, а размеры принимают такие, чтобы обеспечить наибольшую близость поверхности эллипсоида к поверхности геоида. Общеземной эллипсоид используют при решении глобальных геодезических задач, и в частности, при обработке спутниковых измерений. В настоящее время широко пользуются двумя общеземными эллипсоидами: ПЗ-90 (Параметры Земли 1990 г, Россия) и WGS-84 (Мировая геодезическая система 1984 г, США).

 Референц-эллипсоид – эллипсоид, принятый для геодезических работ в конкретной стране. С референц-эллипсоидом связана принятая в стране система координат. Параметры референц-эллипсоида подбираются под условием наилучшей аппроксимации данной части поверхности Земли. При этом совмещения центров эллипсоида и Земли не добиваются.

В России с 1946 г. в качестве референц-эллипсоида используется эллипсоид Красовского с параметрами: а = 6 378 245 м, a = 1/ 298,3.

Системы высот

Счет высот в инженерной геодезии ведут от одной из уровенных поверхностей.

Высотой точки называют расстояние по отвесной линии от точки до уровенной поверхности, принятой за начало счета высот.

Если высоты отсчитывают от основной уровенной поверхности, то есть от поверхности геоида, их называют абсолютными высотами. На рис. 2.5 отрезки отвесных линий Аа и Вв - абсолютные высоты точек А и В.

Если за начало счета высот выбрана какая-либо другая уровенная поверхность, то высоты называют условными. На рис. 2.5 отрезки отвесных линий Аа ¢ и Вв ¢ - условные высоты точек А и В.

В России принята Балтийская система высот. Счет абсолютных высот ведут от уровенной поверхности, проходящей через нуль Кронштадтского футштока.

Численное значение высоты принято называть отметкой. Например, если высота точки А равна H_А = 15,378 м, то говорят, что отметка точки равна 15,378 м.

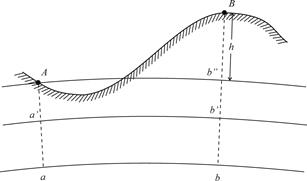
Рис. 2.5. Абсолютные и условные высоты: a¢b¢ – уровенная поверхность; ab –поверхность геоида; Ab² – уровенная поверхность точки A;

Разность высот двух точек называется превышением. Так, превышение точки В над точкой А равно

h_AB = H _В - H_A.

Зная высоту точки А, для определения высоты точки В на местности измеряют превышение h_AB. Высоту точки В вычисляют по формуле

H _В = H_A + h_AB.

Измерение превышений и последующее вычисление высот точек называется нивелированием.

Абсолютную высоту точки следует отличать от ее геодезической высоты, то есть высоты, отсчитываемой от поверхности земного эллипсоида (см. раздел 2.2). Геодезическая высота отличается от абсолютной высоты на величину отклонения поверхности геоида от поверхности эллипсоида.

В заключение отметим, что точное определение положения поверхности геоида в области материков невозможно. Поэтому в России принято отсчитывать высоты от близкой к геоиду, но доступной точному определению вспомогательной поверхности, названной квазигеоидом. Высоты, отсчитываемые от поверхности геоида, называются ортометрическими высотами, а отсчитываемые от поверхности квазигеоида – нормальными высотами. На результаты измерений, выполняемых в инженерной геодезии, различия в двух названных системах высот влияния не оказывают, и в дальнейшем мы их различать не будем, а будем пользоваться введенным выше обобщенным понятием – абсолютные высоты.   

 

Углы ориентирования

Ориентировать линию – значит определить её направление относительно исходного направления, например, меридиана или оси абсцисс х системы плоских прямоугольных координат.

Угол, измеряемый по ходу часовой стрелки от северного направления меридиана до заданного направления, называется азимутом.

Если исходным направлением служит геодезический меридиан, то азимут называют геодезическим азимутом. Если – астрономический, то - астрономическим азимутом. Обобщением обоих понятий служит термин - географический азимут или просто - азимут.

Значения азимута лежат в пределах от 0° до 360°. На рис. 3.1, а обозначено: С – северное направление меридиана, угол А₁ – азимут направления на точку 1 и А₂ – азимут направления на точку 2.

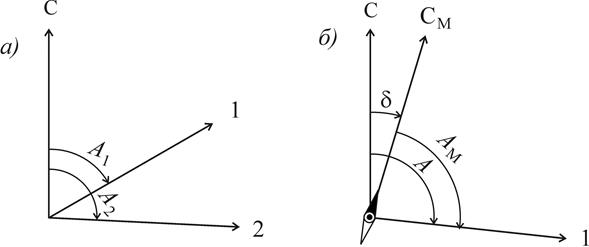
Рис. 3.1. Углы ориентирования: а - азимуты географические; б - магнитный азимут

На местности азимут заданного направления можно определить астрономическим методом - измерив горизонтальный угол между направлением на небесное светило (Солнце, звезду) и заданным направлением. Зная азимут светила, вычисляемый с использованием астрономического ежегодника, и измеренный угол, соображают азимут заданного направления.

Угол, отсчитываемый от северного направления магнитной стрелки до заданного направления, называется магнитным азимутом.

    Магнитная стрелка компаса отклоняется от направления истинного меридиана на угол d, который называется склонением магнитной стрелки (рис. 3.1, б).

    Если северный конец магнитной стрелки отклоняется от меридиана к востоку, то склонение называют восточным и считают положительным, а если - к западу, то называют западным и считают отрицательным.

    Азимут с магнитным азимутом связывает формула:

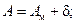
где А - азимут, А_м - магнитный азимут и d – склонение магнитной стрелки.

Магнитные азимуты в геодезии измеряют буссолью (рис. 3.2). Однако точность этих измерений невысока (несколько минут), так как склонение магнитной стрелки непостоянно. На территории России оно меняется от места к месту в пределах от –15° до 25°. В аномальных районах (например, в районе Курской магнитной аномалии) эти изменения так велики, что магнитной стрелкой пользоваться нельзя. Кроме того, склонение изменяется во времени, испытывая суточные, годовые и вековые изменения.

Рис. 3.2. Буссоль

Углом ориентирования, применяемым при использовании системы плоских прямоугольных координат Гаусса-Крюгера, является дирекционный угол.

    Дирекционным углом называется угол между северным направлением осевого меридиана или линии ему параллельной и заданным направлением (рис. 3.3).

Угол g между северным направлением меридиана и направлением оси абсцисс х прямоугольных координат (то есть линии, параллельной осевому меридиану) называется сближением меридианов.

 

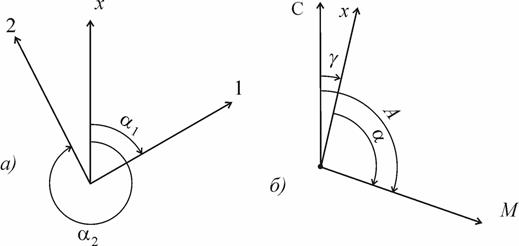
Рис. 3.3. Углы ориентирования: а - дирекционные углы a₁, a₂; б - азимут A и дирекционный угол a

 

При отклонении оси абсцисс от меридиана к востоку, сближение меридианов считают положительным, а при отклонении к западу - отрицательным. При этом справедлива формула (рис. 3.3 б)

А = a + g,

где a - дирекционный угол, g - сближение меридианов.

    Приближенно сближение меридианов равно

g = Dl sinj,

где Dl = l-l₀, причем l -долгота географического данной точки и l₀ - долгота осевого меридиана; j - широта точки.

    На рис. 3.4 показано соотношение между азимутами и дирекционными углами в пределах одной координатной зоны. Легко заметить, что для точек, расположенных к востоку от осевого меридиана зоны, сближение меридианов положительное, а к западу – отрицательное. При этом дирекционные углы в разных точках прямой линии равны a₁ = a₂ = a₃. Поэтому обратный дирекционный угол в точке 3 отличается от прямого в точке 1 ровно на 180°, то есть a_1-3 = a_3-1 ± 180°. Азимуты же в разных точках прямой различаются: А₁ ¹ А₂ ¹ А₃, что обусловлено различием сближения меридианов. Поэтому и А_1-3 ¹ А_3-1 ± 180°.

 

 

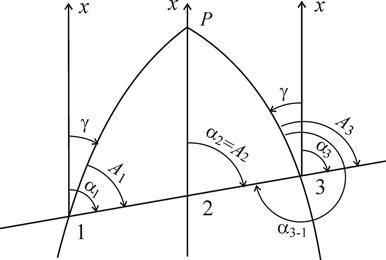
Рис. 3.4. Связь между азимутами и дирекционными углами: 1 – в западной половине зоны; 2 – на осевом меридиане; 3 – в восточной половине зоны; Р – полюс; 1Р, 3Р – меридианы; 2Р – осевой меридиан.

 

При использовании местной системы прямоугольных координат направление оси абсцисс x не связано с направлением осевого меридиана координатной зоны, и тогда дирекционные углы отсчитывают от положительного направления оси абсцисс х.

В практике вычислений находят применение также вспомогательные углы ориентирования – румбы. Румбом называют острый угол, измеряемый от ближайшего направления меридиана (северного или южного). Румбу приписывают название координатной четверти (СВ, ЮВ, ЮЗ, СЗ), в которой расположено заданное направление. Например, для a = 240°36¢ румб равен r = ЮЗ: 60°36¢.

ПЛАН И КАРТА

 

План, карта, цифровая модель местности

Планом называется уменьшенное подобное изображение горизонтальной проекции небольшого участка местности.

Для составления плана местности расположенные на ней точки проецируют на уровенную поверхность по направлению отвесных линий. Ввиду малости участка отвесные линии оказываются практически параллельными, а фрагмент уровенной поверхности может рассматриваться как плоскость. Полученную проекцию местности уменьшают и изображают на плане. Степень уменьшения характеризуется масштабом плана.

Масштабом называется отношение длины отрезка на плане к длине горизонтальной проекции соответствующего отрезка местности. Масштаб записывают в виде дроби с числителем, равным единице, и знаменателем, показывающим, во сколько раз уменьшены на плане длины линий. При строительстве железных дорог для выбора варианта трассы используют планы масштабов 1:2000 и 1:5000, для рабочего проектирования - 1:1000 и 1:2000, для проектирования мостов, тоннелей, станций - 1:500 ¸ 1:2000.

Наряду с представлением масштаба в виде дроби (численного масштаба) пользуются именованным масштабом - его словесным описанием, например: “в одном сантиметре 20 метров”, что соответствует масштабу 1:2000.

Для измерения расстояний на плане, под его нижней рамкой, помещают линейный масштаб (рис. 4.1), на котором несколько раз отложено одно и то же расстояние, называемое основанием масштаба и равное обычно 2 см. Крайнее левое основание делят на более мелкие отрезки. Деления линейного масштаба оцифровывают в метрах.

 

Рис. 4.1 Линейный масштаб

Картой называют уменьшенное и обобщённое изображение на плоскости всей земной поверхности или значительных её частей. Для изготовления карты объекты местности проецируют на поверхность земного эллипсоида и полученное изображение переносят на плоскость. Такой перенос невозможно выполнить без искажений. Каковы будут искажения, определяется картографической проекцией – законом перехода от геодезических координат объектов к плоским координатам карты. В геодезии чаще всего пользуются равноугольными (или иначе - конформными) проекциями, сохраняющими без искажений углы и очертания малых объектов. Карты различаются также по виду изображения на них меридианов и параллелей. В конических проекциях параллели изображаются концентрическими окружностями, а меридианы – радиальными прямыми, углы между которыми пропорциональны разностям долгот. Если при этом углы между изображениями меридианов равны разностям долгот, проекция называется азимутальной. В цилиндрических проекциях линии меридианов и параллелей изображаются взаимно перпендикулярными прямыми. 

Топографические карты в России издают в поперечной цилиндрической проекции Гаусса - равноугольной проекции, в которой прямыми линиями без искажений изображаются осевой меридиан зоны и экватор.

В условиях применения компьютерных технологий, наряду с изображениями местности на бумажных носителях - картами и планами, используются их цифровые аналоги.

Цифровой моделью местности (ЦММ) называется представленное в виде цифровых кодов и хранимое на магнитных носителях логико-математическое описание местности, адекватное по содержанию плану местности. Основным содержанием ЦММ является топографическая информация: координаты и высоты точек, очертания объектов, их свойства. ЦММ содержит и общую информацию - название участка, систему координат и высот и др.

Цифровой картой называют цифровую модель значительного участка земной поверхности, сформированную с учётом генерализации изображаемых объектов и принятой картографической проекции.

Электронной картой называется изображение местности на экране дисплея, полученное на основе цифровой карты.

4.2. Разграфка и номенклатура топографических карт и планов

Топографические карты издают на листах со сторонами 40–50 см. В основу разграфки (нарезки) карт положена карта масштаба 1:1000000. Она издается на листах размерами 4° по широте и 6° по долготе. Множество листов такой карты по направлению параллелей образует ряды шириной по 4°, а по направлению меридианов - колонны шириной по 6°.

Таблица 4.1

Обозначе-ние ряда	Границы ряда по широте	Обозначе-ние ряда	Границы ряда по широте	Обозначе-ние ряда	Границы ряда по широте
A	0° - 4°	I	32° - 36°	Q	64° - 68°
B	4 – 8	J	36 – 40	R	68 – 72
C	8 – 12	K	40 – 44	S	72 – 76
D	12 – 16	L	44 – 48	T	76 – 80
E	16 – 20	M	48 – 52	U	80 – 84
F	20 – 24	N	52 – 56	Y	84 – 88
G	24 – 28	O	56 – 60	Z	88 – 90
H	16 – 20	P	60 – 64

 

Ряды обозначают заглавными буквами латинского алфавита A, B, C, D, ..., начиная от экватора по направлениям к северу и югу (табл. 4.1). Колонны нумеруют арабскими цифрами 1, 2, ... , 60, начиная от меридиана 180° в направлении с запада на восток. Каждому листу карты масштаба 1:1000000 присвоен номенклатурный номер, состоящий из буквы соответствующего ряда и номера колонны, например, M-42.

Для карт масштаба 1:500000 лист масштаба 1:1000000 меридианом и параллелью делят на 4 листа, обозначая их прописными буквами А, Б, В, Г. Номенклатурные номера листов карты образуют добавлением соответствующей буквы к номенклатурному номеру листа масштаба 1:1000000 (например, M-42-Г).

Для карт масштаба 1:200000 лист масштаба 1:1000000 делят на 36 листов, нумеруя их римскими цифрами I, II, ... , XXXVI.

Для карт масштаба 1:100000, разделив лист масштаба 1:1000000 по широте и долготе на 12 частей, получают границы 144 листов (рис. 4.2, а), которые нумеруют цифрами 1, 2, ... , 144. Номенклатура каждого листа складывается из номенклатуры листа масштаба 1:1000000 и номера листа. На рисунке выделен лист M-37-87.

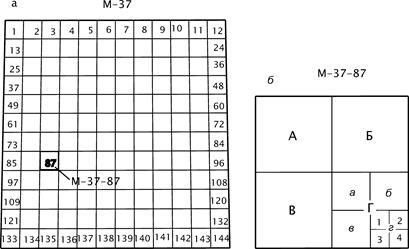
Рис. 4.2. Разграфка листов карт масштабов: а – 1:100000; б – 1:50000, 1:25000, 1:10000.

Разграфка карт масштабов 1:50000, 1:25000 и 1:10000 формируется делением на четыре части листа более мелкого масштаба (соответственно - 1:100000, 1:50000, 1:25000) и добавлением к номенклатуре предыдущего масштаба соответствующего знака, как показано на рис. 4.2, б и в табл. 4.2.

 

Таблица 4.2

	Номенклатура	Число листов	Размеры листа
Масштаб	(последнего листа карты)	карты	По Широте	по долготе
1:1000000 1:100000 1:50000 1:25000 1:10000	M -37 M -37-144 M -37-144-Г M -37-144-Г-г M -37-144-Г-г-4	- 12´12=144 2´2=4 2´2=4 2´2=4	4° 20¢ 10¢ 5¢ 2¢30²	6° 30¢ 15¢ 7¢30² 3¢45²

Для планов масштабов 1:5000 и 1:2000 применяется два вида разграфки - трапециевидная, в которой рамками планов служат параллели и меридианы, и прямоугольная, в которой рамки совмещают с линиями сетки прямоугольных координат.

При трапециевидной разграфке границы листов планов масштаба 1:5000 получают делением листа масштаба 1:100000 на 256 частей (16´16), которые нумеруют от 1 до 256. Номенклатура, например листа №70, записывается так M-37-87(70).

Разграфку листов масштаба 1:2000 получают делением листа масштаба 1:5000 на 9 частей (3´3) и обозначают добавлением буквы русского алфавита, например, M -37-87(70-и).

Прямоугольная разграфка применяется для планов населённых пунктов и для участков площадью менее 20 км2, а также для планов масштабов 1:1000 и 1:500.

При съёмке отдельного участка план может быть составлен и на листе нестандартного формата.

 

4.3. Условные знаки топографических карт и планов

Рамки карты и координатные линии. Листы топографических карт имеют три рамки: внутреннюю, минутную и внешнюю. Внутреннюю рамку образуют отрезки параллелей, ограничивающих площадь карты с севера и юга, и отрезки меридианов, ограничивающих её с запада и востока. Значения широт и долгот на линиях внутренней рамки связаны с номенклатурой карты и написаны в каждом её углу.

Между внутренней и внешней рамками помещена минутная рамка, на которой нанесены деления, соответствующие одной минуте широты (слева и справа) и долготы (наверху и внизу). Точками на рамке отмечены десятки секунд.

Система прямоугольных координат на карте представлена километровой сеткой, образованной проведенными через 1 км координатными линиями x и y. Значения x и y, выраженные в километрах, надписаны на выходах линий за внутреннюю рамку карты.

Планы масштабов 1:5000-1:500 с прямоугольной разграфкой имеют только сетку прямоугольных координат. Ее линии проведены через 10 см.

Условные знаки. На планах и картах объекты местности изображают условными знаками.

Условные знаки различают контурные, внемасштабные и линейные.

Контурными условными знаками изображают объекты, форма и размеры которых могут быть переданы в масштабе плана (карты). К ним относятся земельные угодья (леса, сады, пашни, луга), водоёмы, а для более крупных масштабов - здания, сооружения. Очертания объектов (контуры) на плане показывают точечным пунктиром или линиями определённой толщины и цвета. Внутри контура помещают знаки, указывающие характер объекта.

Внемасштабными условными знаками изображают объекты, которые необходимо нанести на план, но невозможно изобразить в масштабе (бензоколонки, колодцы, пункты геодезической сети и др.).

Линейными условными знаками изображают объекты, длина которых выражается в масштабе плана, а ширина не выражается (линии электропередач и связи, трубопроводы, ограды, тропы).

Для отражения характеристик изображаемых объектов многие условные знаки сопровождаются пояснительными подписями. Так, при изображении железной дороги указывают высоту насыпи и глубину выемки, ширину колеи на узкоколейной дороге. При изображении шоссе указывают его ширину и материал покрытия; при изображении линий связи – число проводов и их назначение; при изображении лесов – породу деревьев, среднюю высоту, толщину стволов и расстояние между деревьями.

Изображение рельефа. На картах и планах рельеф изображают с помощью горизонталей, высотных отметок и условных знаков. 

Горизонтали - линии сечения земной поверхности равноотстоящими уровенными поверхностями. Иными словами, горизонтали - это линии равных высот. Горизонтали, подобно другим точкам местности, проецируют на уровенную поверхность Q и наносят на план (рис. 4.3).

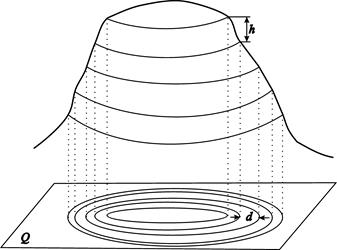
Рис. 4.3. Горизонтали: h – высота сечения рельефа; d – заложение

Разность h высот смежных горизонталей, равная расстоянию между секущими поверхностями, называется высотой сечения рельефа. Значение высоты сечения подписывают у нижней рамки плана.

Горизонтальное расстояние между соседними горизонталями называется заложением. Минимальным в данном месте является заложение, перпендикулярное к горизонталям, – заложение ската. Чем меньше заложение ската, тем круче скат.

Направление ската указывают бергштрихами - короткими штрихами у некоторых горизонталей, направленными в сторону спуска. На отдельных горизонталях в их разрывах пишут их высоту так, чтобы верх цифр указывал в сторону подъёма.

Горизонтали с круглыми значениями высот делают утолщёнными, а для отражения деталей рельефа используют полугоризонтали – штриховые линии, соответствующие половине высоты сечения рельефа, а также вспомогательные горизонтали с короткими штрихами, проводимые на произвольной высоте.

Изображение рельефа горизонталями дополняется вписыванием на план отметок высот около характерных точек рельефа и специальными условными знаками, изображающими обрывы, скалы, овраги и т. п.

Основными формами рельефа являются гора, котловина, хребет, лощина и седловина (рис. 4.4).

 

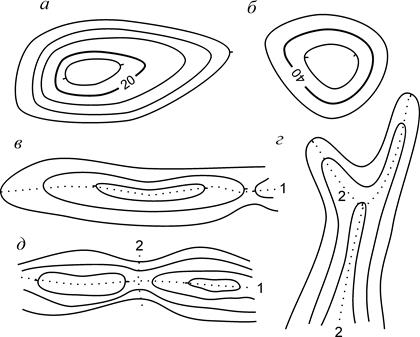
Рис. 4.4. Основные формы рельефа: а – гора; б – котловина; в – хребет; г – лощина; д – седловина; 1 – водораздельная линия; 2 – водосливная линия.

 

Гора (возвышенность, холм, курган, сопка) изображается замкнутыми горизонталями с бергштрихами, обращёнными наружу (рис. 4.4, а). Характерными точками горы являются её вершина и точки у подошвы.

Котловина (впадина) тоже изображается замкнутыми горизонталями, но с бергштрихами, обращёнными внутрь (рис. 4.4, б). Характерными точками котловины являются точки на её дне и вдоль бровки.

Хребет - вытянутая возвышенность. Изображается огибающими гребень хребта и идущими по его скатам вытянутыми горизонталями (рис. 4.4, в). Бергштрихи, как и у горы, обращены наружу. Характерной линией хребта является проходящая вдоль его гребня водораздельная линия.

Лощина (долина, ущелье, овраг, балка) – вытянутое в одном направлении углубление. Изображается вытянутыми, горизонталями с бергшрихами, обращёнными внутрь (рис. 4.4, г). Характерной линией лощины является водосливная линия (тальвег) - линия, по которой сбегает вода.

Седловина (перевал) – понижение между двумя возвышенностями (рис. 4.4, д). По обе стороны к седловине примыкают лощины. Седловина – это место пересечения водораздельной и водосливной линий.

ГЕОДЕЗИЧЕСКИХ ИЗМЕРЕНИЙ

Погрешности измерений

Геодезические работы связаны с выполнением измерений различных величин - расстояний, превышений, углов и др. Измерения могут выполняться непосредственным сравнением измеряемой величины с единицей меры – прямые измерения, и посредством ее вычисления как функции других непосредственно измеренных величин – косвенные измерения.

Результаты измерений всегда содержат некоторые погрешности. Погрешностью Δ называют отклонение результата измерения l от истинного значения измеряемой величины Х.

Δ = l – Х                                               (5.1)

Погрешности проявляются, например, при многократном измерении одной и той же величины – получаемые результаты всегда несколько различаются между собой, и значит, неизбежно отличаются от истинного значения, т.е. содержат погрешности.

Причинами, порождающими погрешности результатов измерений, являются несовершенство измерительных приборов, несовершенство органов чувств наблюдателя, внешние условия, влияющие на измерения.

Измерения, выполненные однотипными приборами, одинаковыми методами и в одинаковых условиях, принято считать равноточными, а выполненные разными приборами и методами, в разных условиях считают неравноточными.

Различают три основных вида погрешностей: случайные, систематические и грубые.

Грубые погрешности – необычно большие погрешности, вызванные небрежностью наблюдателя, неисправностью прибора или резким отклонением от нормы условий измерений. Грубые погрешности выявляют путем выполнения и анализа избыточных измерений. Результаты измерений, содержащие грубые погрешности, отбрасывают, бракуют.

Систематические погрешности – такие, которые при повторных измерениях остаются постоянными, или изменяются закономерным образом.

Причины и закономерности появления систематических погрешностей должны быть изучены, и сами погрешности исключены из результатов измерений путем введения соответствующих поправок, применением надлежащих методик измерений, юстировкой приборов.

Случайные погрешности – такие, которые при повторных измерениях изменяются случайным образом. Ни знак, ни значение случайной погрешности предвидеть невозможно. Поэтому невозможно исключить случайные погрешности из результатов измерений. Можно лишь при обработке измерений ослабить их влияние. Пути к такому ослаблению указывает теория погрешностей измерений.

В дальнейшем будем полагать, что результаты измерений свободны от грубых и систематических и содержат только случайные погрешности.

Измеренных величин.

В практике геодезических измерений определяемые величины обычно являются функциями других, непосредственно измеряемых величин. Рассмотрим функцию u независимых переменных x, y, z , …

u = f (x , y , z …).                                          (5.5)

Продифференцируем функцию (5.5) по всем переменным и заменим дифференциалы du, dx, dy, dz, …. погрешностями Du, Dx, Dy, Dz, ….

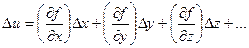
Получили выражение случайной погрешности Du в зависимости от случайной комбинации погрешностей Dx, Dy, Dz, …. Положим, что имеем n таких комбинаций, которым соответствует n выражений:

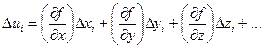         (i = 1, 2, …, n)

Возведем полученные выражения в квадрат, сложим и разделим на n:

,

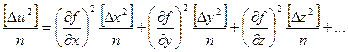
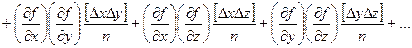где квадратными скобками обозначены суммы.

Устремим число комбинаций в бесконечность (n ® ¥) и, воспользовавшись выражениями (5.4) и (5.3), получим: 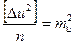, , 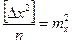, , 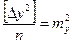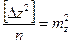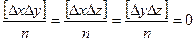. И окончательно

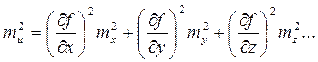                     (5.6)

Итак, квадрат средней квадратической погрешности функции общего вида равен сумме квадратов произведений частных производных по каждой переменной, умноженных на их средние квадратические погрешности.

Частные случаи.

1. Функция u является суммой переменных x , y, z: 

u = x + y + z .

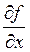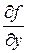В этом случае =1, =1, 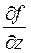=1. Следовательно

= + + .

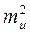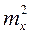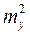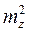2. Функция u является разностью переменных x и y: 

u = x - y.

В этом случае 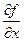=1, 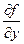=-1. Следовательно

= + .

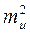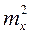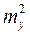3. Функция u имеет вид: 

u = k × x,

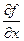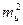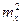где k – постоянный множитель. Теперь = k, поэтому = k²×  и

m_u = k × m_x.

4. Функция u является линейной функцией от x, y, z, …:

u = k₁ x + k₂ y + k₃ z …,

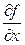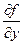где k _i ­постоянные множители. Теперь частные производные равны =k₁, = k₂, 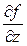= k₃. Поэтому

.

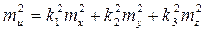Рассмотрим примеры.

Пример 1. Определить среднюю квадратическую погрешность превышения, вычисленного по горизонтальному расстоянию d=124,16 м и углу наклона n=2°16´, если m_d = 0,06 м, а m_n = 1´.

Превышение вычисляют по формуле

h = d tgν.

Продифференцируем формулу по переменным d и n:

, .

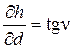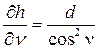Используя формулу общего вида (5.6) получим

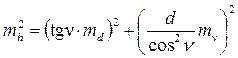
Подставляя исходные данные, найдем

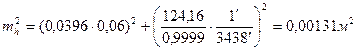
где 3438¢ -­ число минут в радиане. И окончательно m _h=0,036 .м.

Пример 2. При геометрическом нивелировании (см. раздел 9.2) превышение вычисляют как разность отчетов по рейкам

h = a - b.

Отчеты берут с точностью m_a = m_b = 2 мм. Находим среднюю квадратическую погрешность превышения

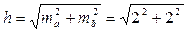= 2,8 мм

Пример 3. Выведем формулу допустимой угловой невязки замкнутого теодолитного хода (см. раздел 9.4). Невязку вычисляют по формуле

f_b = b₁ + b₂ + ¼+ b_n - 180°(n - 2),

где b_i – измеренные углы (i = 1, 2, ¼, n) и n – их число.

Невязка - результат погрешностей в углах b_i. Поэтому средняя квадратическая погрешность невязки равна

m_f = = ,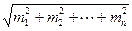

где m₁ = m₂ = ¼ = m_n = m – средняя квадратическая погрешность измерения угла. Примем ее равной m = 0,5¢.

Допуском угловой невязки (f_b)_доп служит предельная погрешность (f_b)_пред=2m_f. Получаем формулу

(f_b)_доп = 1¢ .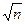

Равноточных измерений

Арифметическая средина результатов равноточных измерений. Пусть имеем результаты многократных равноточных измерений одной величины: l₁, l₂, …, l_n. Рассмотрим их среднее арифметическое

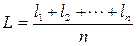.                                 (5.7)

Из (5.1) следует l _i = Х + Δ_i (i = 1, 2, … n). Поэтому напишем

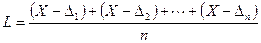= X - .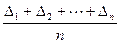

Согласно (5.2) с увеличением числа измерений сумма случайных погрешностей, деленная на их число, стремится к нулю, и, следовательно, среднее арифметическое L стремится к истинному значению Х. Поэтому значение определяемой величины принимают равным среднему арифметическому.

Средняя квадратическая погрешность арифметической средины. Пусть точность результатов измерений l₁, l₂, …, l_n характеризуется средними квадратическими погрешностями

m₁ = m₂ = ¼ = m_n = m

и требуется найти среднюю квадратическую погрешность M арифметической средины.

Представим формулу (5.7) в следующем виде:

L = .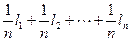

Среднюю квадратическую погрешность арифметической средины найдем как погрешность функции измеренных величин по формуле (5.6)

 

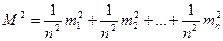
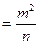
или

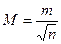                                            (5.8)

Формула (5.8) показывает, что погрешность арифметической средины с ростом числа измерений убывает пропорционально квадратному корню из этого числа. Так, чтобы погрешность среднего арифметического уменьшить в 2 раза, число измерений надо увеличить в 4 раза.

Обработка результатов равноточных измерений. Математическая обработка ряда результатов l₁, l₂, …, l_n прямых равноточных измерений одной величины выполняется в следующей последовательности:

1. Вычисляют среднее арифметическое L

.

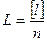2. Вычисляют поправки к v_i результатам измерений

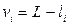(i = 1, 2, …, n)

Контролем правильности вычислений служит сумма поправок, которая должна быть близка к нулю.

3. Вычисляют среднюю квадратическую погрешность одного измерения по формуле Бесселя:

.

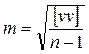Значение m вычисляют с двумя-тремя значащими цифрами.

4. Вычисляют среднюю квадратическую погрешность среднего арифметического

 .

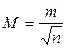Неравноточных измерений

Веса измерений. Неравноточными называют измерения, выполненные приборами различной точности, разным числом приемов, в различных условиях.

При неравноточных измерениях точность каждого результата измерений характеризуется своей среднеквадратической погрешностью. Наряду со средней квадратической погрешностью при обработке неравноточных измерений пользуются относительной характеристикой точности – весом измерения. Вес i-го измерения вычисляют по формуле

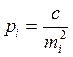                                              (5.9)

где с – произвольная постоянная, назначаемая вычислителем, m_i – средняя квадратическая погрешность i-го измерения.

Так, имея ряд результатов измерений l₁, l₂, ..., l_n , со средними квадратическими погрешностями m₁ ,  m₂ , ..., m_n , определяют их веса:

p₁ = c / m₁² , p₂ = c / m₂² , ..., p_n = c / m_n².

Часто постоянную с для удобства дальнейших вычислений назначают так, чтобы веса p_i оказались целыми числами.

Рассмотрим смысл произвольной постоянной с. Предположим, что в результате фиксирования значения с вес j-го измерения стал равен 1, то есть p_j = c / m_j² = 1. Отсюда находим c = m_j². Следовательно, постоянная с есть квадрат средней квадратической погрешности m² такого измерения, вес которого принят за единицу (с = m²).

Теперь (5.9) можем записать так

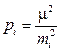.                                           (5.10)

Кратко m называют средней квадратической погрешностью единицы веса. 

Вес арифметической средины. Рассмотрим вес арифметической средины равноточных измерений. Примем в формуле (5.8) за единицу вес одного измерения, то есть m = m, и запишем .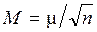

Тогда согласно (5.10) вес Р арифметической средины L будет равен

P = 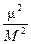 = n.                                (5.11)

Вывод. Если за единицу веса принят вес одного измерения, то согласно (5.11) вес арифметической средины равен числу измерений.

Следствие. Если результат l измерения имеет вес р, то можем считать, что l является средним арифметическим из р измерений с весом 1.

Общая арифметическая средина результатов неравноточных измерений. Пусть имеем результаты многократных неравноточных измерений одной величины: l₁, l₂, …, l_n, выполненных с весами p₁, p₂, …, p_n.

Представим каждый из результатов l_i (i = 1, 2, …, n) как среднее из p_i результатов с весом 1. Получим такой ряд результатов равноточных измерений:

l₁ - результат p₁ измерений с весом 1,

l₂ - результат p₂ измерений с весом 1,

¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼

l_n - результат p_n измерений с весом 1,

где общее число измерений с весом 1 равно p₁ + p₂ +¼+ p_n .

Нами составлен ряд результатов равноточных измерений, позволяющий найти окончательное значение измеряемой величины как среднее арифметическое из всех результатов измерений

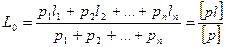.                             (5.12)

Значение, вычисляемое по формуле (5.12), называют общей арифметической срединой или весовым средним.

Оценки точности результатов неравноточных измерений. Приведем без вывода формулы характеристик точности, используемых при обработке прямых неравноточных измерений.

Средняя квадратическая погрешность m измерения, имеющего вес, равный единице:

- формула Гаусса: .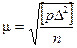  

Формула применяется, когда известно достаточно точное, близкое к истинному, значение X измеряемой величины.

- формула Бесселя:  ,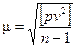

где v _i - поправки к результатам измерений:

.

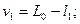
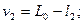
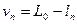Средняя квадратическая погрешность общей арифметической средины

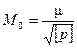
Обработка результатов неравноточных измерений. Математическая обработка ряда результатов прямых неравноточных измерений одной величины выполняется в следующей последовательности.

1. Вычисление весового среднего (общей арифметической средины)

.

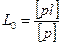2. Вычисление поправок к результатам измерений:

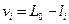(i = 1, 2,…, n).

Контролем правильности вычислений служит равенство

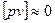
3. Вычисление средней квадратической погрешности одного измерения по уклонениям от арифметической средины, используя формулу Бесселя для неравноточных измерений:

.

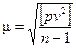4. Вычисление средней квадратической погрешности весового среднего

.

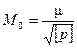ГЕОДЕЗИЧЕСКИЕ СЕТИ

Геодезической сетью называют совокупность пунктов на земной поверхности, закрепленных специальными центрами, положение которых определено в общей для них системе координат и высот.

Различают плановые, высотные и пространственные сети. Плановые сети – это такие, в которых определены плановые координаты (плоские - x, y или геодезические - широта B и долгота L) пунктов. В высотных сетях определяют высоты пунктов относительно отсчетной поверхности, например, поверхности геоида (а точнее - квазигеоида). В пространственных сетях определяют пространственные координаты пунктов, например, прямоугольные геоцентрические X, Y, Z или геодезические B , L , H.

6.1. Методы построения плановых сетей

При построении плановых сетей отдельные пункты сети служат исходными – их координаты должны быть известны. Координаты остальных пунктов определяют с помощью измерений, связывающих их с исходными. Плановые геодезические сети создают следующими методами.

Триангуляция – метод определения планового положения геодезических пунктов путем построения на местности сети треугольников, в которых измеряют углы, а также длины некоторых сторон, называемых базисными сторонами (рис. 6.1).

Положим, что в треугольнике АВ P известны координаты пунктов А ( 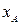, 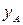) и B ( 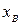, 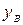). Это позволяет путем решения обратной геодезической задачи определить длину стороны  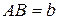и дирекционный угол  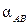направления с пункта A на пункт B. Длины двух других сторон треугольника АВ P могут быть вычислены по теореме синусов

; .

 

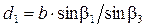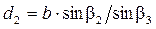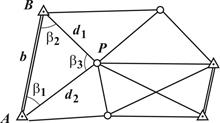
Рис. 6.1. Схема сети триангуляции

 

Продолжая подобным образом, вычисляют длины всех сторон сети. Если, кроме базиса b известны другие базисы (на рис. 6.1 базисы показаны двойной линией), то длины сторон сети можно вычислить с контролем.

Дирекционные углы сторон А P и В P треугольника АВ P равны

; .

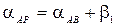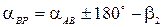Координаты пункта P определятся по формулам прямой геодезической задачи

; .

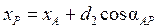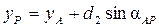Аналогично вычисляют координаты всех остальных пунктов.

Трилатерация – метод определения планового положения геодезических пунктов путем построения на местности сети треугольников, в которых измеряют длины их сторон.

Если в треугольнике АВ P (рис. 6.1) известен базис b и измерены стороны 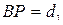 и 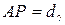, то на основе теоремы косинусов, можно вычислить углы треугольника;

;

;

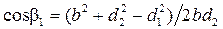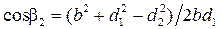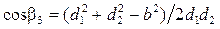.                           (6.1)

Так же вычисляют углы всех треугольников, а затем, как и в триангуляции, - координаты всех пунктов.

Линейно-угловая сеть строится, как правило, как сеть треугольников, в которых измеряют углы и длины сторон. Такие сети имеют большое число избыточных измерений и поэтому отличаются высокой надежностью.

Полигонометрия – метод определения планового положения геодезических пунктов путем проложения ломаной линии (полигонометрического хода) или системы связанных между собой ломаных линий (сети полигонометрии), в которых измеряют углы поворота и длины сторон.

 

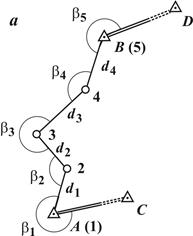
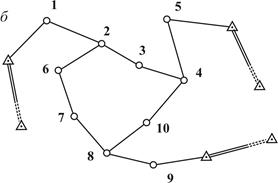
Рис. 6.2. Полигонометрия: а - полигонометрический ход; б – система ходов

Схема полигонометрического хода показана на рис. 6.2 a, где A и B – исходные пункты; CA и BD - исходные направления, дирекционные углы которых известны; 1, 2, 3, 4, 5 - точки (вершины) хода; 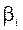- измеренные горизонтальные углы; 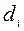- измеренные длины сторон (i = 1, 2, …).

На рис. 6.2 б показана схема системы полигонометрических ходов. Точки 2, 4, 8, где соединяются разные ходы, называются узловыми.

Спутниковый метод определения координат геодезических пунктов основан на измерениях по сигналам спутников навигационных систем ГЛОНАСС (Россия) и GPS (США), выполняемых двумя (и более) наземными приемниками. По результатам измерений с высокой точностью определяют разности 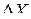, , 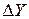 геоцентрических координат между пунктами. Если координаты одного из пунктов известны, то, прибавив к ним измеренные разности, находят координаты остальных пунктов. Затем координаты преобразуют в геодезические или плоские прямоугольные.

6.2. Основные виды плановых геодезических сетей

Геодезические сети по назначению классифицируют на государственные геодезические сети, геодезические сети сгущения, геодезические сети специального назначения и съемочные сети.

Государственная геодезическая сеть. Государственная геодезическая сеть покрывает всю территорию Российской Федерации и служит ее главной геодезической основой.

Государственная геодезическая сеть (ГГС) предназначена для решения следующих основных задач, имеющих хозяйственное, научное и оборонное значение: установление и распространение единой системы координат на всю территорию страны и поддержание ее на уровне современных и перспективных требований; геодезическое обеспечение картографирования территории страны и акваторий окружающих ее морей; геодезическое обеспечение изучения земельных ресурсов и землепользования, кадастра, строительства, разведки и освоения природных ресурсов; обеспечение геодезическими данными средств наземной, морской и аэрокосмической навигации, аэрокосмического мониторинга природной и техногенной среды; изучение поверхности и гравитационного поля Земли и их изменений во времени; изучение геодинамических явлений; метрологическое обеспечение высокоточных технических средств определения местоположения и ориентирования.

Положение пунктов ГГС определено сочетанием методов триангуляции, полигонометрии, астрономических и спутниковых измерений. Каталоги координат пунктов в системе СК-95 (координатная система 1995 года) хранятся в территориальных аэрогеодезических предприятиях Федерального Агентства «Роскартография».

По мере совершенствования средств измерений и накопления новых данных ГГС модернизируется. Создаваемая в настоящее время сеть согласно “Основным положениям о государственной геодезической сети Российской Федерации” включает: фундаментальную астрономо-геодезическую сеть, высокоточную геодезическую сеть, спутниковую геодезическую сеть 1 класса, а также астрономо-геодезическую сеть и геодезические сети сгущения.

Фундаментальная астрономо-геодезическая сеть (ФАГС) - сеть пунктов, геоцентрические координаты которых определяются методами космической геодезии относительно центра масс Земли с погрешностью не более 10-15 см. Расстояния между пунктами 650 - 1000 км.

Высокоточная геодезическая сеть (ВГС) обеспечивает распространение на всю территорию страны геоцентрической системы координат и уточнение параметров связи геоцентрической системы с действующей системой координат СК-95. Пункты ВГС определяются по наблюдениям спутников навигационных систем ГЛОНАСС и GPS. Расстояния между пунктами 150 - 300 км.

Спутниковая геодезическая сеть 1 класса (СГС-1) - сеть, создаваемая по мере необходимости по наблюдениям спутников систем ГЛОНАСС и GPS. Расстояния между пунктами 25 - 35 км.

Характеристики точности рассмотренных выше сетей представлены в табл. 6.1, где D – расстояние между пунктами в км.

Таблица 6.1

Сеть	Расстояние между смежными пунктами, км	Погрешность взаимного положения пунктов
		По плановым координатам	По высоте
ФАГС	650-1000	2 см	3 см
ВГС	150-300	3 мм +0,05 мм · D	5 мм +0,07 мм · D
СГС-1	25-35	3 мм +0,1 мм · D	5 мм +0,2 мм · D

 

 Астрономо-геодезическая сеть включает ранее созданные сети 1 и 2 классов. Сети 1 класса создавались в виде звеньев длиной 200 - 250 км, расположенных главным образом вдоль меридианов и параллелей и образующих замкнутые полигоны периметром 800 - 1000 км. Сеть 2 класса - сплошная сеть внутри полигонов. Сети 3 и 4 классов опираются на пункты 1 и 2 классов и служат сгущению сети.

Сети сгущения. Там, где требуется дальнейшее сгущение сети (например, в населенных пунктах), опираясь на государственную геодезическую сеть, развивают сети сгущения 1 и 2 разряда, чем достигается плотность на 1 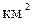не менее 4 пунктов на застроенной территории и 1 пункт на незастроенной территории.

Геодезические сети специального назначения создают в тех случаях, когда требуется особо высокая точность геодезической сети. Геодезическую сеть специального назначения строят в государственной или в местной системе координат. Примерами таких сетей являются создаваемые на железных дорогах реперные системы, которые должны служить основой для всех съемочных и разбивочных геодезических работ, возникающих при проектировании, строительстве и текущем содержании железных дорог, а также для мониторинга пути и сооружений, межевания земель и кадастровой съемки в пределах полосы отвода.

Съемочную сеть создают при выполнении съемки местности. Она развивается от пунктов государственной геодезической сети и сетей сгущения 1 и 2 разрядов. Но при съемке отдельных участков съемочная сеть может быть и самостоятельной, построенной в местной системе координат. В съемочных сетях, как правило, одновременно определяют положение пунктов в плане и по высоте.

Предельные погрешности планового положения пунктов съемочной сети относительно исходных пунктов не должны превышать на открытой местности и на застроенной территории 0,2 мм в масштабе плана и 0,3 мм на местности, закрытой древесной и кустарниковой растительностью.

Координаты пунктов съемочных сетей определяют проложением теодолитных ходов, построением триангуляции, засечками, спутниковым методом и др. Наиболее распространены теодолитные ходы.

6.3. Закрепление пунктов плановых геодезических сетей

Пункты геодезических сетей закрепляют на местности специальными знаками - центрами, призванными обеспечить устойчивость и длительную сохранность пунктов.

Вид центра зависит от назначения сети и характера грунта. Официальными нормативными документами [16, 17, 21] установлены типовые конструкции центров, зависящие от класса пункта и местных условий. Они различны для районов сезонного промерзания грунтов, для районов многолетней мерзлоты, для районов распространения подвижных песков.

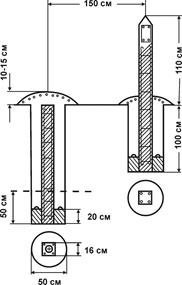
На рис. 6.3 показан центр пункта государственной геодезической сети 1 - 4 классов для районов сезонного промерзания грунта. Центр представляет собой железобетонный пилон сечением 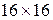см и скрепленный с ним цементным раствором якорь диаметром 50 см и высотой 20 см. Основание центра располагают на 50 см ниже границы наибольшего промерзания грунта, но во всех случаях не менее 1,5 м от поверхности земли. На верху пилона крепится (цементным раствором или приваривается) чугунная марка, на верхней поверхности которой отмечена точка, к которой относятся координаты пункта.

В 1,5 м устанавливают способствующий отысканию центра опознавательный знак – железобетонный столб с укрепленной на нем металлической охранной плитой, обращенной в сторону центра.

До внедрения в геодезическое производство спутниковых технологий над центрами геодезических пунктов устанавливались наружные геодезические знаки - деревянные или металлические сооружения, служащие объектом визирования на пункт и для подъема геодезических приборов над землей. Основными типами наружных знаков являлись пирамида и сигнал (рис. 6.4).

 

Рис. 6.3. Центр геодезического пункта: - - - - - - граница промерзания грунта	Рис. 6.4. Геодезические знаки: слева – пирамида; справа – сигнал

 

243 00,0

          B  

 

         

Sb = 466°51,2′

P = Sd = 452,10

SDx = = -122,60         SDy = = +342,89           

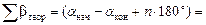
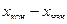= -122,70;  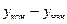 = 343,01;

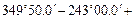= 4×180° -

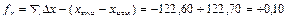м

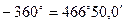
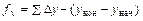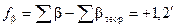
= + 342,89 - 343,01 = - 0,12 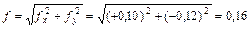м

м

                 

 

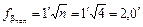
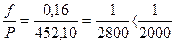
Вычисленную угловую невязку сравнивают с допустимой

.

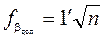Если угловая невязка меньше допустимой, что указывает на доброкачественность угловых измерений и правильность вычислений, то невязку 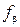  распределяют поровну во все измеренные углы со знаком, противоположным знаку невязки. Полученные при этом поправки

 

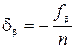
вписывают над измеренными углами в графу 2. Невязка редко делится на число углов без остатка. Поэтому поправки округляют, вводя бо¢льшие в углы с более короткими сторонами. При этом сумма поправок должна равняться невязке с обратным знаком: Sd_b = -f_b.

Вычисление дирекционных углов. Дирекционные углы вычисляют, используя начальный дирекционный угол 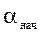и измеренные углы b_i, исправленные поправками d_b, по формулам:

для правых углов - ;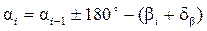

для левых углов -  .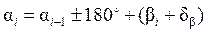

Здесь индексы i = 1, 2, …, n соответствуют номерам углов и сторон на рис. 6.5 а, причем a₀ = a_нач и a_n = a_кон.

    Контролем правильности вычислений служит равенство вычисленного и заданного значений конечного дирекционного угла.

Вычисление приращений координат выполняют по дирекционным углам и длинам сторон хода (графы 5 и 6).

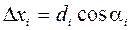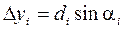;  (i = 1, 2, …, n-1).

    Вычислив суммы приращения абсцисс 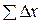 и ординат 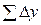, находят координатные невязки

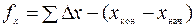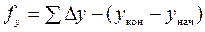                ,  .    (6.3)            

Вычисляют абсолютную невязку 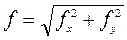и относительную невязку хода f / P, где  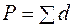- длина хода. Если относительная невязка не превосходит допустимой (обычно, 1/2000), то невязки f_x и f_y распределяют (см. записи курсивом в графах 5 и 6), в виде поправок к приращениям координат, пропорциональных длинам сторон, и со знаками, противоположными знакам невязок:

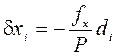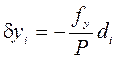; .                        (6.4)

Суммы поправок должны равняться невязкам с обратным знаком:

; .

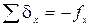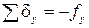Если из-за выполненных округлений равенства нарушаются, поправки, вычисленные по формулам (6.4), несколько изменяют, добиваясь соблюдения равенств.

Вычисление координат точек теодолитного хода выполняют по формулам (см. графы 7 и 8)

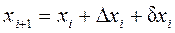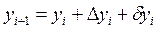;      (i = 1, 2, …, n-1).

Контролем правильности вычислений служит совпадение вычисленных и заданных координат последней точки теодолитного хода.

Обработка замкнутого теодолитного хода.

Последовательность обработки замкнутого хода такая же как и разомкнутого. Но исходными в замкнутом теодолитном ходе служат координаты одного из пунктов хода и дирекционный угол одной из сторон. Это накладывает на обработку замкнутого хода следующие особенности.

 Угловая невязка вычисляется по формуле (6.2), в которой в отличие от разомкнутого хода

,

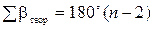где n – число углов в полигоне.

После распределения угловой невязки и вычисления дирекционных углов сторон хода контролируют правильность вычислений - в конце должно быть получено то же значение дирекционного угла, которое было исходным.

Невязки в координатах находят по формулам:

, .

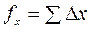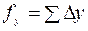Эти соотношения следуют из формул (6.3), где в данном случае 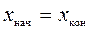, 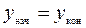. Распределив невязки f_x и f_y и вычислив координаты точек хода, контролируют правильность вычислений - вычисленные в конце координаты начальной точки хода должны равняться исходным.

Измерение углов

Определения

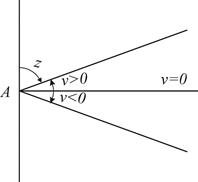
Горизонтальным углом называют проекцию b пространственного угла ÐCAB (рис. 7.1) на горизонтальную плоскость P. Для измерения горизонтального угла, образуемого направлениями A С и A В, необходимо круг с делениями расположить горизонтально, совместив его центр с отвесной линией AA¢, проходящей через вершину угла A, и определить число делений круга между проекциями направлений A С и A В на плоскость круга.

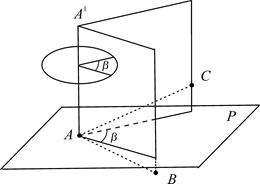
Вертикальные углы - это углы, расположенные в вертикальной плоскости (рис. 7.2). Углом наклона линии называют угол n между направлением линии и её проекцией на горизонтальную плоскость. Углы наклона выше горизонта - положительные, ниже горизонта - отрицательные. Зенитное расстояние – угол z между направлением в зенит и направлением линии.

                                  

Рис. 7.1. Горизонтальный угол¢	Рис. 7.2. Вертикальные углы

Горизонтальные и вертикальные углы измеряют теодолитами.

Устройство теодолитов

Принципиальная схема устройства теодолита показана на рис. 7.3. В отверстие подставки 2, опирающейся на три подъёмных винта 1, входит ось вращения лимба 3, в которую в свою очередь входит ось алидады 4.

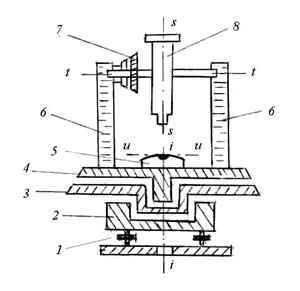
Рис. 7.3. Схема устройства теодолита: ii - ось вращения алидады; tt - ось вращения трубы; ss - визирная ось трубы; uu - ось уровня алидады.

Лимб это стеклянный круг, по скошенному краю которого нанесены деления с оцифровкой от 0 до 360º по часовой стрелке.

Алидада - верхняя часть прибора, расположенная соосно с лимбом. Алидада несет стойки 6, на которые опирается ось tt вращения зрительной трубы 8 с вертикальным кругом 7. Установка оси ii вращения алидады в отвесное положение выполняется тремя подъёмными винтами подставки по цилиндрическому уровню 5.

Вращающиеся части теодолита снабжены закрепительными винтами для их установки в неподвижное положение и наводящими винтами для плавного их вращения.

Зрительная труба служит для обеспечения точности наведения на визирные цели. Трубы бывают с прямым и обратным изображением.

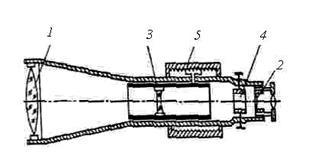
Рис. 7.4. Зрительная труба

Оптическая система трубы (рис. 7.4.) состоит из объектива 1, окуляра 2 и фокусирующей линзы 3, которую с помощью специального устройства - кремальеры 5, перемещают вдоль геометрической оси трубы. Между фокусирующей линзой и окуляром помещена сетка нитей 4 – деталь, несущая стеклянную пластину с нанесёнными на нее вертикальными и горизонтальными штрихами. При измерении углов перекрестие штрихов – центр сетки нитей, наводят на изображение визирной цели.

Сетка нитей имеет четыре исправительных винта, позволяющих перемещать ее в горизонтальном и вертикальном направлениях.

Линия, проходящая через оптический центр объектива и перекрестие сетки нитей, называется визирной осью.

Увеличением трубы называется отношение угла, под которым изображение предмета видно в трубе, к углу, под которым предмет виден невооружённым глазом. Практически увеличение трубы равно отношению фокусного расстояния объектива к фокусному расстоянию окуляра. Трубы геодезических приборов имеют увеличение от 15^´ до 50^´ и более.

Полем зрения трубы называется пространство, видимое в трубу при её неподвижном положении. Обычно оно бывает от 1 до 2º.

Визированием называют наведение трубы на цель. Точность визирования зависит от увеличения трубы и приближенно равна

,

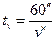где v^´ – увеличение зрительной трубы, а 60²– средняя разрешающая способность глаза.

Для визирования трубу фокусируют “по глазу” и “по предмету”. При этом, глядя в трубу, вращением диоптрийного кольца окуляра добиваются чёткого изображения сетки нитей, а перемещением фокусирующей линзы 3 - чёткого изображения наблюдаемого предмета.

Отсчётные устройства служат для взятия отсчетов по горизонтальному и вертикальному кругам. Они снабжены отсчетными микроскопами. Различают микроскопы штриховые, шкаловые и микроскопы с оптическими микрометрами.

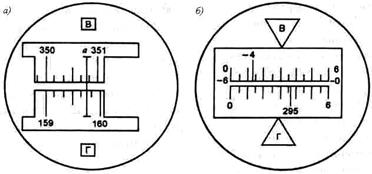
В штриховом микроскопе отсчет с точностью 1¢ берут по положению нулевого штриха алидады а (рис. 7.5, а), интерполируя минуты на глаз.

 

в)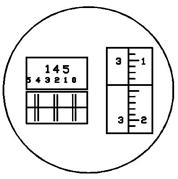

Рис. 7.5. Поле зрения отсчётных микроскопов:

а - штрихового (отсчёт по горизонтальному кругу 159º46’, по вертикальному 350º48’); б - шкалового (отсчёт по горизонтальному кругу 295º36’, по вертикальному -4º47’);

в - оптического микрометра (отсчет 145º23’14’’).

Шкаловый микроскоп имеет две шкалы, совмещённые с лимбами вертикального и горизонтального кругов (рис. 7.5, б). Отсчёты берут по градусным штрихам лимбов. Шкала вертикального круга теодолита 2Т30 имеет два ряда подписей. Если перед градусным делением отсутствует знак, отсчёт делают так же, как и по горизонтальному кругу. Если перед цифрой градусов стоит минус, то минуты считывают по шкале от -0 до -6 (справа налево).

Точные теодолиты снабжены микроскопами с оптическим микрометром (рис. 7.5, в). Градусы отсчитывают по основной шкале после совмещения верхнего и нижнего изображений штрихов горизонтального (или вертикального) круга, а минуты и секунды читают по шкале микрометра.

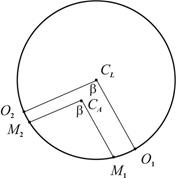
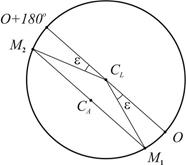
Эксцентриситет алидады. Несовпадение оси вращения алидады C_A (рис. 7.6) с центром лимба C_L называется эксцентриситетом алидады и является причиной систематических погрешностей при измерении углов. Так, при повороте алидады на угол b (рис. 7.6 а) вместо верной разности отсчетов по лимбу О₂ – О₁ из-за эксцентриситета алидады будет получена разность M₂ – M₁.

При отсутствии эксцентриситета поворот алидады на 180° (см. рис. 7.6 б) вызывает изменение отсчета на 180°. А при наличии эксцентриситета отсчеты до и после поворота различаются не ровно на 180°, так как содержат одинаковые погрешности эксцентриситета e, но с разным знаком. Так на рис. 7.6 б отсчет M₁ больше верного отсчета O на угол e, а отсчет M₂ меньше верного отсчета на угол e.

 

a)                                                                б)

Рис. 7.6. Эксцентриситет алидады: а – влияние на результат измерения угла; б – исключение влияния; C_L – центр лимба; C_A – ось вращения алидады.

Для исключения погрешности эксцентриситета горизонтальные углы измеряют при двух положениях вертикального круга – круг слева и круг справа. При этом отсчётное устройство обеспечивает взятие отсчетов на противолежащих частях лимба. Среднее из результатов, полученных при круге слева и круге справа, свободно от ошибки эксцентриситета.

Высокоточные теодолиты имеют двухсторонние отсчетные устройства, обеспечивающие одновременное взятие отсчетов по противоположным частям лимба. 

Уровни служат для приведения осей и плоскостей приборов в горизонтальное или вертикальное положение. По конструкции они бывают цилиндрические и круглые.

 

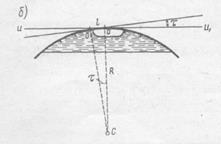
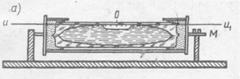Рис. 7.7. Цилиндрический уровень: а – общий вид; б – цена деления уровня.

Цилиндрический уровень (рис. 7.7.) состоит из стеклянной ампулы, верхняя внутренняя поверхность которой отшлифована по дуге окружности определённого радиуса. При изготовлении уровня её заполняют горячим эфиром или спиртом и запаивают. При охлаждении в ампуле образуется небольшое пространство, заполненное парами жидкости и называемое пузырьком уровня. Ампула помещается в металлическую оправу, снабжённую исправительными винтами для регулировки положения уровня (на рис. 7.7, а - винт М). На внешней поверхности ампулы нанесена шкала со штрихами через 2 мм. Точка в середине шкалы называется нульпунктом уровня. Касательная к внутренней поверхности ампулы в нульпункте называется осью уровня. Пузырёк уровня занимает в ампуле наивысшее положение, поэтому, когда его концы расположены симметрично относительно нульпункта, ось уровня горизонтальна.

Центральный угол t (рис. 7.7, б), соответствующий одному делению шкалы, называется ценой деления уровня. Цена деления уровня, выраженная в секундах, определяется по формуле

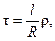
где l - длина деления шкалы; R - радиус внутренней поверхности ампулы; ρ - число секунд в радиане. В разных типах теодолита цена деления цилиндрического уровня бывает от 15² до 60².

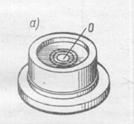
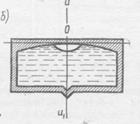
У круглого уровня (рис. 7.8.) внутренняя поверхность верхней стеклянной части ампулы имеет сферическую поверхность. Шкала уровня имеет вид окружностей с общим центром, который служит нульпунктом.

 

Рис. 7.8. Круглый уровень:

а – вид сверху; б –разрез и ось уровня

Нормаль к внутренней сферической поверхности ампулы в нульпункте называется осью круглого уровня. При расположении пузырька уровня в нульпункте ось уровня занимает отвесное положение. Цена деления круглого уровня бывает в пределах 3 - 15’. Круглые уровни служат для предварительной установки прибора в рабочее положение.

Разновидности теодолитов. В зависимости от точности теодолиты подразделяют на высокоточные (Т1), точные (Т2, Т5) и технические (Т15, Т30, Т60). Цифрами здесь указана точность измерения горизонтального угла одним приемом в лабораторных условиях, выраженная в секундах.

Различаются теодолиты и по конструкции.

Так, для измерения вертикальных углов точные теодолиты снабжены уровнем при вертикальном круге. У технических теодолитов такого уровня нет, его роль выполняет уровень при алидаде горизонтального круга. Есть теодолиты, в которых уровень при вертикальном круге заменен автоматическим компенсатором углов наклона (теодолиты Т5К, Т15К).

Теодолиты бывают с трубами прямого и обратного изображения. В первом случае в шифр теодолита добавляют букву П (Т5КП, Т15КП, Т15МКП). Маркшейдерские теодолиты (Т30М, Т15М), предназначенные для подземных работ, где возможно наличие взрывоопасного газа метана, изготавливают в специальном исполнении.

Электронные теодолиты (например, Т5Э) обеспечивают автоматическое считывание отсчетов по горизонтальному и вертикальному кругам. Угломерная часть электронного теодолита представляет собой растровый датчик накопительного типа. Датчиком угла служит стеклянный круг с нанесенным на него штрих-кодом. Сигнал, прочитанный фотоприемником, поступает в электронную часть датчика угла, обрабатывается и выводится в градусной мере на дисплей и в память прибора. Наличие двухосевого компенсатора обеспечивает автоматический ввод поправок за наклон в отсчеты по горизонтальному и вертикальному кругам.

Электронный теодолит является важной частью современного универсального прибора – электронного тахеометра.

Поверки теодолита

Поверки теодолита выполняют для контроля соблюдения в приборе верного взаиморасположения его осей. Основными поверками являются следующие.

Поверка уровня. Ось цилиндрического уровня на алидаде горизонтального круга должна быть перпендикулярна к оси вращения алидады.

Перед выполнением поверки выполняют горизонтирование теодолита. Затем устанавливают уровень по направлению двух подъёмных винтов и с их помощью приводят пузырёк в нульпункт. Поворачивают алидаду на 180º. Если пузырёк уровня остался в нульпункте, то требуемое условие выполнено – ось уровня перпендикулярна к оси вращения алидады. Если пузырёк уровня ушел из нульпункта, исправительными винтами уровня изменяют его наклон, перемещая пузырёк в сторону нульпункта на половину отклонения.

Поверку повторяют, добиваясь, чтобы смещение пузырька было меньше одного деления.

Поверка сетки нитей. Вертикальный штрих сетки нитей должен быть перпендикулярен к оси вращения зрительной трубы.

Наводят вертикальный штрих сетки нитей на точку и наводящим винтом трубы изменяют ее наклон. Если изображение точки не скользит по штриху, сетку нитей надо повернуть. Для этого поворачивают корпус окуляра, ослабив четыре винта его крепления к зрительной трубе (рис. 7.9).

 

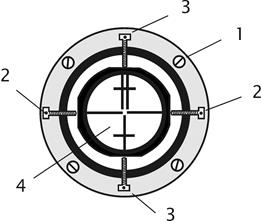
Рис. 7.9. Крепление сетки нитей: 1- крепёжный винт окуляра; 2, 3 - горизонтальные и вертикальные исправительные винты сетки нитей; 4 – сетка нитей.

Поверка визирной оси. Визирная ось трубы должна быть перпендикулярна к оси вращения трубы.

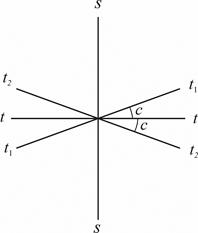
Если визирная ось перпендикулярна к оси вращения трубы, то отсчёты по горизонтальному кругу при разных положениях вертикального круга (круг слева и круг справа) и наведении на одну и ту же точку будут различаться ровно на 180º. Если разность отчетов отличается от 180°, то ось вращения трубы не перпендикулярна к визирной оси (рис. 7.10). При этом соответствующие отсчёты Л и П отличаются от правильных значений на одинаковую величину с, получившую название коллимационной ошибки.

При выполнении поверки визируют на удалённую точку при двух положениях круга и берут отсчёты Л и П. Вычисляют коллимационную погрешность с = (Л - П ± 180°) ¤ 2, которая не должна превышать двойной точности теодолита. 

Если коллимационная погрешность велика, то наводящим винтом алидады устанавливают на горизонтальном круге верный отсчёт, равный (Л - с) или (П + с). При этом центр сетки нитей сместится с изображения точки. Отвинчивают колпачок, закрывающий винты сетки нитей, ослабляют один из вертикальных исправительных винтов, и, действуя горизонтальными исправительными винтами, совмещают центр сетки нитей с изображением точки. Закрепив ослабленные винты, поверку повторяют.

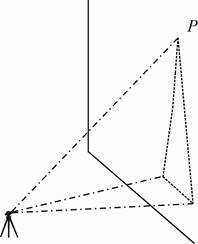
Рис. 7.10. Поверка визирной оси: ss - визирная ось; tt - верное положение оси вращения трубы; t1t1, t2t2 -положение оси вращения трубы при круге право и круге лево.	Рис. 7.11. Поверка оси вращения зрительной трубы

Поверка оси вращения трубы. Ось вращения трубы должна быть перпендикулярна к оси вращения алидады.

Установив теодолит вблизи стены здания, визируют на высоко расположенную под углом наклона 25 - 30º точку Р (рис. 7.11). Наклоняют трубу до горизонтального положения и отмечают на стене проекцию центра сетки нитей. Переводят трубу через зенит, вновь визируют на точку Р и отмечают её проекцию. Если изображения обеих проекций точки не выходят за пределы биссектора сетки нитей, требование считают выполненным. В противном случае необходимо исправить положение оси вращения трубы. Исправление выполняют в мастерской, изменяя наклон оси.

 

ИЗМЕРЕНИЕ ДЛИН ЛИНИЙ

Нитяный дальномер

Теория нитяного дальномера. Зрительные трубы многих геодезических приборов снабжены нитяным дальномером. Сетка нитей зрительной трубы, кроме основных штрихов (вертикальных и горизонтальных), имеет дальномерные штрихи a и b (рис. 8.4, а). Расстояние D от оси вращения прибора MM (рис. 8.4, б) до рейки AB равно

D = L + f + d ,

где L - расстояние от фокуса объектива до рейки; f - фокусное расстояние; d - расстояние между объективом и осью вращения прибора.

Лучи, идущие через дальномерные штрихи сетки a и b параллельно оптической оси, преломляются объективом, проходят через его фокус F и проецируют изображения дальномерных штрихов на точки A и B, так что дальномерный отсчёт по рейке равен n. Обозначив расстояние между дальномерными штрихами p, из подобных треугольников ABF и a¢b¢F находим L = n f / p. Обозначив f / p = K и f + d = c , получаем

D = K n + c ,

где K - коэффициент дальномера и  c - постоянная дальномера.

 

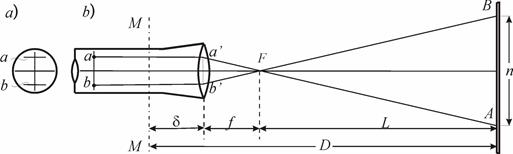
Рис. 8.4. Нитяный дальномер: а) – сетка нитей; б) – схема определения расстояния

При изготовлении прибора f и p подбирают такими, чтобы K=100, а постоянная c была близкой к нулю. Тогда D = 100 n.

Точность измерения расстояний нитяным дальномером » 1/300.

Определение горизонтального проложения линии, измеренной нитяным дальномером. При измерении наклонной линии отсчёт по рейке это отрезок n = AB (рис. 8.5). Если бы рейку наклонить на угол n, то отсчёт был бы равен n₀ = A₀B₀ = n cosn и наклонное расстояние D = Kn₀+ c = Kn ×cosn+c.

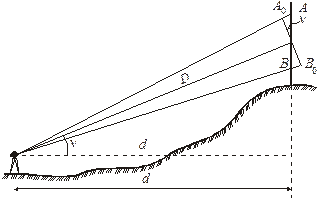
Рис. 8.5. Измерение нитяным дальномером наклонного расстояния

Умножив наклонное расстояние D на cosn, получим горизонтальное расстояние d = K n cos2 n + c cos n.

Прибавив и отняв с × cos2n, после преобразований получим

d = (Kn + с) cos²n + 2c cosn sin²(n¤2).

Методы нивелирования

Нивелированием называется измерение превышений с целью определения высот точек. Путем нивелирования значения высот передают от исходных точек с известными высотами на точки, высоты которых надо определить.

В зависимости от применяемых приборов и методов различают следующие виды нивелирования.

Геометрическое нивелирование - метод определения превышений путем взятия отсчетов по вертикальным рейкам при горизонтальном луче визирования. Это - основной метод нивелирования. Методом геометрического нивелирования создана государственная нивелирная сеть, создаются инженерно-геодезические высотные сети различного назначения.

 Тригонометрическое нивелирование - метод определения превышения путем измерения вертикального угла и расстояния. Метод используют при создании высотного обоснования топографических съемок, а также при определении превышений и передаче высот на строительных площадках.

Барометрическое нивелирование основано на зависимости между высотой и атмосферным давлением. Для определения превышений измеряют атмосферное давление и температуру в точке с известной высотой и в точках, высоты которых определяют. По разностям давлений вычисляют превышения. Метод применяют при работах в труднодоступной местности, им пользуются геологи, геофизики. Точность измерений этим методом невысокая: на равнинной местности - 0.5 м, в горной - 1.5 м.

Гидростатическое нивелирование основано на свойстве жидкости в сообщающихся сосудах устанавливаться на одном уровне. Простейший  гидростатический нивелир представляет собой два сосуда с делениями, соединенные шлангом. Систему заполняют дистиллированной водой. Точность метода очень высокая (0,1 мм), поэтому он применяется при монтаже и выверке конструкций по высоте, особенно при работе в стесненных условиях, при передаче отметок через водные преграды, для наблюдений за деформациями сооружений (плотин, мостов, ускорителей частиц и пр.).

Определение превышений и высот точек с помощью спутниковых измерений. Автономное определение высот точек аппаратурой ГЛОНАСС и GPS выполняется с точностью нескольких метров, а определение превышений между точками - с точностью 10 - 15 мм.

Рис. 9.2. Нивелирный ход

    Превышения вычисляют по формулам (см. рис. 9.2):

h₁ = a₁ - b₁;

h₂ = a₂ - b₂;

h₃ = a₃ - b₃;

Превышение между конечными точками хода А и В равно сумме вычисленных превышений

h_AB = h₁  + h₂ + h₃,

а высота точки В определится по формуле (9.1).

Нивелиры

Нивелиры с уровнем при трубе снабжены точным цилиндрическим уровнем, приводимым для измерений вместе со зрительной трубой в горизонтальное положение вручную. Нивелирами с уровнем при трубе являются нивелиры российского производства Н-3, Н-05, 3Н5Л и др.

Нивелиры с компенсатором углов наклона отличаются наличием устройства, автоматически приводящего визирную ось зрительной трубы в горизонтальное положение. Компенсатор работает в пределах 12 - 15¢, поэтому прибор предварительно устанавливают в рабочее положение по круглому уровню. Такими нивелирами являются Н-3К, 3Н2КЛ и др. 

Нивелиры с оптическим микрометром (например, нивелир Н-05) имеют перед объективом стеклянную пластину, повороты которой вокруг ее горизонтальной оси смещают лучи света параллельно самим себе. Это позволяет наводить визирную ось точно на штрих рейки. Величина смещения измеряется оптическим микрометром, чем достигается высокая точность отсчета по рейке.

Лазерные нивелиры излучают видимый пучок света. Отсчет берут по световому пятну на рейке.

Цифровые нивелиры автоматически формируют отсчет по рейке, шкала которой представляет собой штриховой код. Снабжены компенсатором углов наклона. Отсчеты по рейкам регистрируются на магнитном носителе. Примером такого прибора является нивелир SDL30M, Япония.    

По точности нивелиры делят на высокоточные, точные и технические в зависимости от величины средней квадратической погрешности m_h измерения превышения на 1 км двойного хода (табл. 9.1).

Таблица 9.1

Типы нивелиров	Точность	Примеры нивелиров
Высокоточные	mh £ 0,5 мм	Н-05 (Россия), PL1 (Япония)
Точные	mh £ 3 мм	3Н2КЛ, Н-3, Н-3К (Россия), С300 (Япония), DSZ3(Китай)
Технические	mh £ 5 мм	3Н5Л (Россия), АТ20D (Китай)

Нивелир с уровнем при трубе

Нивелиром с уровнем при трубе является, например, нивелир Н-3. Его устройство показано на рис. 9.3.

Для выполнения измерений нивелир устанавливают на штативе и подъемными винтами 7 приводят в нульпункт пузырек круглого уровня 5. Пользуясь закрепительным 3 и наводящим 4 винтами, наводят зрительную трубу на рейку. Вращением диоптрийного кольца окуляра 10 фокусируют трубу “по глазу” и вращением головки фокусирующего винта 2 - “по предмету”. В поле зрения трубы будут видны штрихи сетки нитей, изображение нивелирной рейки и в отдельном окошке - изображения двух половинок цилиндрического уровня (рис. 9.4).

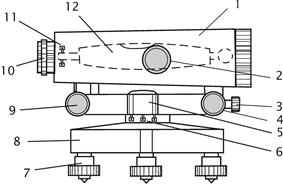
Рис. 9.3. Устройство нивелира Н-3:

Зрительная труба; 2 - фокусирующий винт зрительной трубы; 3, 4 – закрепительный и наводящий винты; 5 – круглый уровень; 6 – исправительные винты круглого уровня; 7 – подъемные винты; 8 - подставка; 9 – элевационный винт; 10 – окуляр с диоптрийным кольцом для фокусировки трубы по глазу; 11 – исправительные винты цилиндрического уровня; 12 – цилиндрический уровень.

 

Вращая элевационный винт 9 (рис. 9.3), изменяющий наклон трубы 1 и цилиндрического уровня 12, приводят ось уровня в горизонтальное положение. Ось уровня горизонтальна, если его пузырек находится в нульпункте, на что указывает совмещение концов изображений половинок уровня в поле зрения трубы (рис. 9.4). Отсчет берут по среднему штриху сетки нитей.

 

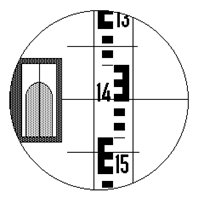
Рис. 9.4. Поле зрения зрительной трубы нивелира: отсчет по рейке равен 1449 мм

Поверки нивелира

Необходимая точность нивелирования может быть достигнута только в том случае, если обеспечено верное взаиморасположение основных осей нивелира. Для контроля предъявляемых к прибору требований в начале и периодически в ходе работ выполняют поверки нивелира. Основными поверками являются следующие.

Поверка круглого уровня. Ось круглого уровня должна быть параллельна оси вращения прибора.

Подъемными винтами нивелира приводят пузырек круглого уровня в нульпункт. Поворачивают нивелир на 180° вокруг оси его вращения ii (рис. 9.5). Если после поворота пузырек остался в нульпункте, проверяемое условие выполнено – ось круглого уровня ee параллельна оси вращения прибора ii.

Если пузырек ушел из нульпункта, исправительными винтами 2 изменяют наклон уровня так, чтобы пузырек сместился в сторону нульпункта на половину отклонения. Для поворота исправительных винтов пользуются шпилькой.

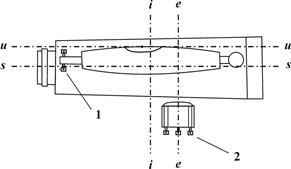
Рис. 9.5. Оси и исправительные винты нивелира: ss – визирная ось зрительной трубы; ii – ось вращения прибора; uu – ось цилиндрического уровня; ee – ось круглого уровня; 1 – исправительные винты цилиндрического уровня; 2 – исправительные винты круглого уровня

Поверка цилиндрического уровня. Ось цилиндрического уровня должна быть параллельна визирной оси зрительной трубы.

У высокоточных и точных нивелиров проекция на отвесную плоскость угла между осью цилиндрического уровня и визирной осью не должна превышать 10". Это означает, что при расстоянии до рейки d = 100 м допустима ошибка в отсчете по рейке из-за непараллельности оси уровня и визирной оси, не превышающая 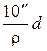= 5 мм, где ρ = 206 265" - число секунд в одном радиане.

Поверка выполняется путем измерения одного и того же превышения дважды - из середины и с неравными расстояниями до реек.

На расстоянии 75 – 100 м друг от друга закрепляют две точки, на которые устанавливают рейки (рис. 9.6). В середине, на равных расстояниях от реек устанавливают нивелир и, приводя пузырек цилиндрического уровня в нульпункт, берут отсчеты a и b по рейкам и вычисляют превышение .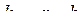

Если визирная ось трубы не параллельна оси уровня и потому наклонена на угол i, то вместо верных отсчетов a и b будут прочтены отсчеты a₁ и b₁. Вследствие равенства расстояний до реек ошибки в обоих отсчетах будут одинаковыми, Da = Db. Вычисленное при этом превышение будет равно

h = a₁ – b₁ = (a + Da) – (b + Db) = a – b.

Следовательно, несмотря на ошибки отсчетов, вызванные непараллельностью оси уровня и визирной оси трубы, превышение, вычисленное по измерениям из середины - верное.

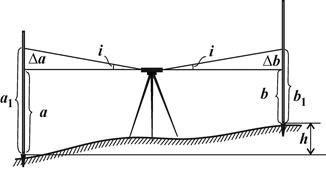
Рис. 9.6. Поверка цилиндрического уровня. Измерения из середины

Нивелир переносят и устанавливают на расстоянии 2-3 м от одной из реек (рис. 9.7). Берут отсчет b₂ по ближней рейке. Ввиду малости расстояния до рейки погрешность в отсчете b₂, вызванная наклоном луча визирования, мала. Поэтому отсчет b₂ считают безошибочным.

Рис. 9.7. Поверка цилиндрического уровня. Измерения с неравными расстояниями до реек

Вычисляют отсчет, который должен быть на дальней рейке, если луч визирования горизонтален: a₀ = b₂ + h.

Наводят нивелир на дальнюю рейку и берут фактический отсчет a₂. Сравнивают вычисленный и фактический отсчеты.

Если вычисленный a₀ и фактический a₂ отсчеты различаются меньше, чем на 5 мм, то считают, что ось цилиндрического уровня uu (рис. 9.5) параллельна визирной оси ss.

Если вычисленный и фактический отсчеты различаются больше, чем на 5 мм, то положение цилиндрического уровня необходимо исправить.

Для этого элевационным винтом наводят средний штрих сетки нитей на отсчет a₀ по дальней рейке. При этом пузырек цилиндрического уровня уйдет из нульпункта. Вертикальными исправительными винтами приводят пузырек цилиндрического уровня в нульпункт, совмещая изображения концов половинок пузырька в поле зрения трубы.

У нивелиров с компенсатором углов наклона цилиндрического уровня нет, и при выполнении поверки добиваются выполнения следующего условия.

Визирная ось зрительной трубы должна быть горизонтальна в пределах работы компенсатора.

Поверка выполняется в том же порядке, как и поверка цилиндрического уровня. Но при этом различие вычисленного a₀ и фактического a₂ отсчетов указывает на негоризонтальность визирной оси трубы.

Для исправления снимают колпачок, закрывающий исправительные винты сетки нитей зрительной трубы, и с помощью вертикальных исправительных винтов, наводят среднюю нить сетки нитей на отсчет по дальней рейке, равный вычисленному отсчету a₀.

Нивелирные рейки

Для высокоточного нивелирования служат цельные трехметровые инварные рейки. На рейке крепится круглый уровень, используемый для установки рейки в вертикальное положение. 

Для точного и технического нивелирования служат трехметровые цельные или складные деревянные рейки. На двух сторонах рейки нанесены шкалы с сантиметровыми делениями в виде шашек, на одной стороне – черных, на другой – красных. Установка таких реек в вертикальное положение выполняется по круглому уровню или на глаз.

При измерениях цифровыми нивелирами пользуются специальными рейками со шкалой в виде штрих-кода.

Поверки реек состоят в определении с помощью контрольной линейки длины метровых и дециметровых интервалов, определении разности нулей пары реек, поверке установки круглого уровня на рейке.

Нивелирные сети

Нивелирная сеть представляет собой совокупность закрепленных на местности точек, высоты которых определены путем геометрического нивелирования.

Основой для определения высот пунктов в России служит государственная нивелирная сеть I, II, III и IV классов.

Главной высотной основой страны является государственная нивелирная сеть I и II классов, назначением которой является распространение единой системы высот на территорию всей страны. Нивелирные сети I и II классов используются также для решения таких научных задач, как изучение фигуры физической поверхности Земли и ее гравитационного поля, определение разностей высот уровней морей и океанов, изучение вертикальных движений земной коры и др.

Государственная нивелирная сеть I класса имеет наивысшую точность и служит исходной для сетей следующих классов. Нивелирная сеть II класса опирается на пункты I класса, является ее сгущением. Невязки в сетях I и II классов не должны превышать соответственно 3мм× и 5мм× 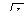, где L – длина нивелирного хода, выраженная в километрах.

Нивелирные сети  III и IV классов опираются на сеть I и II классов и служат основой для создания  высотного обоснования топографических съемок местности и решения различных инженерных задач. Невязки в таких сетях не должны превышать соответственно 10мм× 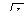 и 20мм× .

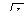Пункты государственной нивелирной сети надежно закрепляют на местности с помощью знаков – реперов. В зависимости от условий местности и характера грунта реперы бывают грунтовые, скальные и стенные.

Грунтовый репер состоит из железобетонного пилона сечением 16х16 см с маркой вверху и бетонной плитой (якорем) внизу. Марка должна находиться на 0,5 м ниже поверхности земли, а якорь - не менее чем на 0,5 м ниже глубины сезонного промерзания грунта.

Скальный репер представляет собой вцеменированную в скалу чугунную марку.

Стенной репер – представляет собой вцементированную в стену чугунную марку с выступом для установки на него нивелирной рейки или отверстием для ее подвешивания. Стенные реперы закладывают в цокольной части фундаментальных зданий или сооружений (опора моста, здание пассажирского вокзала, водонапорная башня).

На застроенной территории реперы закладывают не реже, чем через 5 км, а на незастроенной – не реже, чем через 7 км.

Нивелирование с точностью II, III и IV класса применяется не только в государственной нивелирной сети, но и при геодезическом обеспечении строительства и эксплуатации различных сооружений. Так, на железных дорогах с помощью геометрического нивелирования решаются такие задачи, как съемка профиля пути на станциях и перегонах, контроль проектного уклона путей на сортировочных горках, съемка продольного и поперечных профилей на вновь сооружаемых и реконструируемых железных дорогах, создание высотных съемочных сетей для съемки станций и узлов, создание высотной основы для строительства мостов и тоннелей и др.

Нивелирование II класса используют при наблюдениях за осадками зданий и сооружений.

Техническое нивелирование. На изысканиях железных дорог и других линейных сооружений, при создании высотного съемочного обоснования выполняют техническое нивелирование.

Ход технического нивелирования начинают и заканчивают на пунктах более высокого класса. По форме такие ходы бывают разомкнутыми или замкнутыми.

Для измерения превышений используются точные или технические нивелиры (табл. 9.1).

Ход прокладывают в одном направлении.

Нивелир устанавливают по возможности на равных расстояниях от передней и задней реек (см. рис. 9.2). При этом расстояния до реек не должны превышать 150 м.

Отсчеты по рейкам берут по среднему штриху сетки нитей, придерживаясь следующей последовательности - отсчет по черной стороне задней рейки, отсчет по черной стороне передней рейки, отсчет по красной стороне передней рейки, отсчет по красной стороне задней рейки.

Вычитая из отсчетов по задней рейке отсчеты по передней рейке, вычисляют превышения по черным и красным сторонам, а затем – среднее превышение h_ср. Контролем правильности измерений служит разность между превышениями, полученными по черным и красным сторонам реек. Расхождение не должно превышать 5 мм.

Контролем точности измерений в ходе служит невязка f_h, которую вычисляют по формулам:

- в разомкнутом ходе

f_h = å h_ср - (H_кон - H_нач);                                (9.2)

- в замкнутом ходе

f_h = å h_ср .                                          (9.3)

Здесь Sh_ср - сумма средних превышений в ходе; H_кон и H_нач - высоты конечного и начального реперов.

Невязка f_h считается допустимой, если она не превышает 50мм× 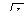, где L – длина хода, выраженная в километрах.

 Невязку равномерно распределяют в измеренные превышения. Поправку к превышению вычисляют по формуле δ_h = - f_h / n, где n – число превышений в ходе. Поправками исправляют измеренные превышения: 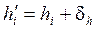. Используя исправленные превышения, последовательно вычисляют отметки всех точек нивелирного хода.

H_i+1 = H_i + 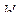         (i = 1, 2, …, n)

9.9. Тригонометрическое нивелирование

Тригонометрическое нивелирование – определение превышений по измеренным вертикальным углам и расстояниям.

Для определения превышения между точками А и B (рис. 9.9) на точке А устанавливают теодолит, а на точке B – рейку. Теодолитом измеряют угол наклона n.

Если известно горизонтальное расстояние d между точками А и B, то превышение h вычисляют по формуле:

h = d ×tgn + k - l,                                      (9.4)

где n - угол наклона, k - высота прибора, l - высота визирования.

Если расстояние AB измерено нитяным дальномером, то горизонтальное расстояние равно d = K n cos²n, где K – коэффициент дальномера и n – отсчет по рейке. Подставляя это выражение для d в (9.4) получаем h = K n cos2n tg n +k – l и окончательно  

h = 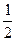Kn sin2n + k – l                                  (9.5)

Рис. 9.9. Тригонометрическое нивелирование

 

Формула (9.5) находит применение при тахеометрической съемке местности и носит название тахеометрической формулы для превышений.

ЛИТЕРАТУРА

 

1. Визгин А.А., Коугия В.А., Хренов Л.С. Практикум по инженерной геодезии. Учебное пособие для вузов.. – М.: Недра, 1989. – 285 с.

2. Генике А.А., Побединский Г.Г. Глобальные спутниковые системы определения местоположения и их применение в геодезии. Изд. 2-е. – М.: Картгеоцентр, 2004. – 355 с.

3. Геодезия. Термины и определения. ГОСТ 22268-76. – М.:Госстандарт СССР, 1976. – 32 с.

4. Геодезия. Топографические съемки: Справочное пособ. / Ю.К. Неумывакин, Е. И. Халугин, П. Н. Кузнецов и А. В. Бойко – М.: Недра, 1991. – 317 с.: ил.

5. Геодезические работы при строительстве мостов / В.А.Коугия, В.В. Грузинов, О.Н. Малковский, В.Д. Петров. – М.: Недра, 1986. – 248 с.

6. Изыскания и проектирование железных дорог. Учеб. для вузов ж.-д. трансп. / И.В. Турбин, А.В. Гавриленков, И.И. Кантор и др.; под ред. И.В. Турбина. – M.: Транспорт, 1989. – 479 с.

7. Инженерная геодезия. Учеб. для вузов ж.-д. трансп./ Г.С. Бронштейн, В.Д. Власов, Н.С. Зайцева и др.; под ред. С.И. Матвеева.– М.; 1999. – 455 с.

8. Инженерная геодезия. Учеб. для вузов / Под ред. Д.Ш. Михелева. – Изд. 2-е – М.: Высш. шк., 2001 – 464 с.

9. Инструкция по нивелированию I, II, III и IV классов.– М.: Недра, 1990. – 167 с.

10. Инструкция по топографической съемке в масштабах 1:5000, 1:2000, 1:1000, 1:500. – М.: Недра, 1985. – 152 с. 

11. Инструкция по топографо-геодезическим работам при инженерных изысканиях для промышленного, сельскохозяйственного, городского и поселкового строительства. СН-212-73. – М.: Стройиздат, 1974. – 152 с.

12. Коськов Б. И. Справочное пособие по съемке городов. – 3-е изд., перераб. и доп. – М.: Недра, 1986. – 334 с.

13. Лобанов А.Н. Аэрофототопография. – М.: Недра, 1978. – 576 с.

14. Матвеев С.И., Коугия В.А., Цветков В.Я. Геоинформационные системы и технологии на железнодорожном транспорте: Учебное пособие для вузов ж.-д. трансп. / Под ред. С.И. Матвеева. – М.: УМК МПС России, 2002. – 288 с.

15. Основные положения о государственной геодезической сети Российской Федерации. ГКИНТП (ГНТА) – 01 – 006 – 03. – М.: Федеральная служба геодезии и картографии России, 2004. – 28 с.

16. Правила закладки центров и реперов на пунктах геодезической и нивелирной сетей. – М.: “Картгеоцентр-Геодезиздат”,1993.

17. Правила закрепления центров пунктов спутниковой геодезической сети. – М.: ЦНИИГАиК, 2001.- 51 с.

18. СНиП №.01.03.-84. Геодезические работы в строительстве. – М.: ЦНИТП Госстроя СССР. – 1985. – 28 с. 

19. Спутниковая технология геодезических работ. Термины и определения / Руководящий технический материал. – М.: ЦНИИГАиК, 2001. – 28 с.

20. Условные знаки для топографических планов масштабов 1:5000, 1:2000, 1:1000, 1:500. – М.: Недра, 1989. - 286 с.

 21. Центры геодезических пунктов для территории городов, поселков и промышленных площадок. – М.: Недра, 1972. – 24 с.

 

Содержание

1. Предмет инженерной геодезии………………………………………………………. 2. Форма и размеры Земли. Системы координат. Высоты……………………………. 2.1. Форма и размеры Земли………………………………………………………. 2.2. Системы координат, применяемые в геодезии……………………………... 2.3. Системы высот………………………………………………………………... 3. Ориентирование линий. Прямая и обратная геодезические задачи на плоскости. 3.1. Углы ориентирования…………………………………………………………. 3.2. Прямая и обратная геодезические задачи на плоскости……………………. 4. План и карта……………………………………………………………………………. 4.1. План, карта, цифровая модель местности………………………………….... 4.2. Разграфка и номенклатура топографических карт и планов……………….. 4.3. Условные знаки топографических карт и планов…………………………… 4.4. Решение задач по топографической карте…………………………………... 4.5. Определение площадей по картам и планам………………………………… 5. Математическая обработка результатов геодезических измерений……………….. 5.1 Погрешности измерений………………………………………………………. 5.2 Свойства случайных погрешностей…………………………………………... 5.3 Характеристики точности измерений………………………………………… 5.4 Средняя квадратическая погрешность функции измеренных величин…….. 5.5 Математическая обработка результатов прямых равноточных измерений .. 5.6 Математическая обработка результатов прямых неравноточных измерений…………………………………………………………………………………... 5.7. Понятие об уравнивании геодезической сети………………………………. 6. Геодезические сети ……………………………………………………………………. 6.1. Методы построения плановых сетей………………………………………… 6.2. Основные виды плановых геодезических сетей…………………………….. 6.3. Закрепление пунктов плановых геодезических сетей………………………. 6.4. Создание съемочных сетей проложением теодолитных ходов…………….. 6.5. Определение координат засечками…………………………………………... 7. Измерение углов………………………………………………………………………. 7.1. Определения …………………………………………………………………... 7.2. Устройство теодолитов ………………………………………………………. 7.3. Измерение горизонтальных углов…………………………………………… 7.4. Измерение вертикальных углов……………………………………………… 7.5. Поверки теодолита …………………………………………………………… 8. Измерение длин линий………………………………………………………………… 8.1. Измерение длин линий мерными лентами и рулетками …………………… 8.2. Определение недоступных расстояний……………………………………… 8.3. Нитяный дальномер…………………………………………………………… 8.4. Светодальномеры, электронные тахеометры ……………………………….. 9. Нивелирование………………………………………………………………………… 9.1. Методы нивелирования………………………………………………………. 9.2. Геометрическое нивелирование……………………………………………… 9.3. Нивелиры ……………………………………………………………………… 9.4. Нивелир с уровнем при трубе ……………………………………………….. 9.5. Поверки нивелира……………………………………………………………... 9.6. Нивелирные рейки…………………………………………………………….. 9.7. Влияние кривизны Земли и рефракции на результаты нивелирования…… 9.8. Нивелирные сети……………………………………………………………… 9.9. Тригонометрическое нивелирование ……………………………………….. 9.10. Теодолитно-высотные и тахеометрические ходы…………………………. Литература………………………………………………………………………………...

3 5 5 6 9 10 10 14 15 15 17 20 22 27 30 30 31 32 33 36   37 40 41 41 43 45 46 50 52 52 53 58 59 60 62 62 67 67 68 72 72 73 75 75 76 79 79 80 82 83 84

 

 

ИНЖЕНЕРНАЯ ГЕОДЕЗИЯ

 

Учебное пособие

 

 

Часть I

 

 

САНКТ-ПЕТЕРБУРГ

2006

УДК 528.48

 

 

Инженерная геодезия. Учебное пособие, часть I / Е.С. Богомолова, М.Я. Брынь, В.В. Грузинов, В.А. Коугия, В.И. Полетаев; под ред. В.А. Коугия. – СПб.: Петербургский гос. ун-т путей сообщения, 2006. - с.

 

 

Изложены предмет и задачи инженерной геодезии, сведения о системах координат и высот, методах построения плановых и высотных геодезических сетей, элементы теории погрешностей измерений, приборы и методы, применяемые для измерения углов и расстояний, приборы и методы нивелирования.

Разделы 1, 6 пособия написаны М.Я. Брынем, 2, 9 – Е.С. Богомоловой, 3 – В.В. Грузиновым, 4, 8 – В.А. Коугия, 5, 7 – В. И. Полетаевым.

Предназначено для студентов, обучающихся по железнодорожным и строительным специальностям.

 

ПРЕДМЕТ ИНЖЕНЕРНОЙ ГЕОДЕЗИИ

Геодезия – наука, изучающая фигуру и внешнее гравитационное поле Земли и разрабатывающая методы создания систем координат, определения положения точек на Земле и околоземном пространстве, изображения земной поверхности на картах.

Научными задачами геодезии являются:

- установление систем координат;

- определение формы и размеров Земли и ее внешнего гравитационного поля и их изменений во времени;

- проведение геодинамических исследований (определение горизонтальных и вертикальных деформаций земной коры, движений земных полюсов, перемещений береговых линий морей и океанов и др.).

Научно-технические задачи геодезии в обобщенном виде заключаются в следующем:

- определение положения точек в выбранной системе координат;

- составление карт и планов местности разного назначения;

- обеспечение топографо-геодезическими данными нужд обороны страны;

- выполнение геодезических измерений для целей проектирования и строительства, землепользования, кадастра, исследования природных ресурсов и др. 

Геодезия в процессе своего развития разделилась на ряд научных дисциплин: высшую геодезию, топографию, фотограмметрию, картографию, космическую геодезию, морскую геодезию, инженерную геодезию.

Особое место в этом ряду занимает инженерная геодезия, которая разрабатывает методы геодезического обеспечения изысканий, проектирования, строительства и эксплуатации инженерных сооружений: железных и автомобильных дорог, мостов, тоннелей, трубопроводов, промышленных и гражданских зданий, систем водоснабжения и водоотведения и др.

Основными задачами инженерной геодезии являются:

- топографо-геодезические изыскания, в ходе которых выполняется создание на объекте работ геодезической сети, топографическая съемка, геодезическая привязка точек геологической и геофизической разведки;

- инженерно-геодезическое проектирование, включающее разработку генеральных планов сооружений и их цифровых моделей; геодезическую подготовку проекта для вынесения его в натуру, расчеты по горизонтальной и вертикальной планировке, определению площадей, объемов земляных работ и др.;

- геодезические разбивочные работы, включающие создание на объекте геодезической разбивочной сети и последующий вынос в натуру главных осей сооружения и его детальную разбивку;

- геодезическая выверка конструкций и технологического оборудования при установке их в проектное положение;

- наблюдения за деформациями сооружений, определяющие осадки оснований и фундаментов, плановые смещения и крены сооружений.

Геодезическое обеспечение строительства и эксплуатации современных инженерных сооружений связано с необходимостью выполнения точных измерений, служащих определению координат и высот геодезических пунктов, составлению топографических карт и планов, продольных профилей трасс; наблюдению за деформациями сооружений. Для обеспечения необходимой точности измерения выполняются высокоточными геодезическими приборами: теодолитами – угловые измерения; светодальномерами – линейные измерения; электронными тахеометрами – угловые и линейные измерения с решением различных инженерно-геодезических задач; нивелирами – определение превышений. При определении положения объектов используется аппаратура, работающая по сигналам спутниковых навигационных систем, при выполнении топографической съемки местности находят применение лазерные сканеры. Обработка результатов геодезических измерений выполняется на современных компьютерах с использованием развитого программного обеспечения. К числу таких программных продуктов относятся геоинформационные системы, служащие сбору, обработке, систематизации, отображению и анализу картографической информации.

Состав геодезических работ, их точность, используемые методы и приборы различаются в зависимости от особенностей объекта.

Так, при выполнении изысканий железной дороги создают геодезическую сеть, опираясь на которую составляют топографические карты и планы. На картах и планах выполняют предварительное трассирование дороги, окончательное положение которой выбирают в поле. Затем делают съемку трассы и получают необходимые для проектирования дороги профиль трассы и ситуационный план полосы местности.

Для обеспечения безопасного движения поездов вдоль железной дороги создают высокоточную геодезическую сеть (так называемую, реперную систему), опираясь на которую выполняют работы по реконструкции и ремонту пути, по оперативному контролю его геометрических параметров, по наблюдениям за деформациями пути, земляного полотна и искусственных сооружений.

В процессе строительства и по мере завершения отдельных его этапов выполняются исполнительные съемки, целью которых является установление точности вынесения проекта сооружения в натуру, выявление отклонений, допущенных в процессе строительства, а также определение фактических координат и высотных отметок построенных объектов, размеров его отдельных частей.

 

ФОРМА И РАЗМЕРЫ ЗЕМЛИ. СИСТЕМЫ КООРДИНАТ.

ВЫСОТЫ

 

Форма и размеры Земли

Изучение формы и размеров Земли включает решение двух задач. Это - установление некоторой сглаженной, обобщенной, теоретической фигуры Земли и определение отклонений от нее фактической физической поверхности.

Учитывая, что поверхность океанов и морей составляет 71% поверхности Земли, а поверхность суши - только 29%, за теоретическую фигуру Земли принято тело, ограниченное поверхностью океанов в их спокойном состоянии, продолженной и под материками, и называемое геоидом.

Поверхность, в каждой своей точке перпендикулярная к отвесной линии (направлению силы тяжести), называется уровенной поверхностью. Из множества уpовенных поверхностей одна совпадает с поверхностью геоида.

Из-за неравномерности распределения масс в земной коре геоид имеет неправильную геометрическую форму, и его поверхность нельзя выразить математически, что необходимо для решения геодезических задач. При решении геодезических задач геоид заменяют близкими к нему геометрически правильными поверхностями.

Так, для приближенных вычислений Землю принимают за шар с радиусом 6371 км.

Ближе к форме геоида подходит эллипсоид – фигура, получаемая вращением эллипса (рис. 2.1) вокруг его малой оси. Размеры земного эллипсоида характеризуют следующими основными параметрами: a - большая полуось, b - малая полуось, a - полярное сжатие и e – первый эксцентриситет меридианного эллипса, где 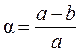 и .

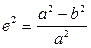Рис. 2.1. Меридианный эллипс: Рс – северный полюс; Рю – южный полюс

 

Различают общеземной эллипсоид и референц-эллипсоид.

Центр общеземного эллипсоида помещают в центре масс Земли, ось вращения совмещают со средней осью вращения Земли, а размеры принимают такие, чтобы обеспечить наибольшую близость поверхности эллипсоида к поверхности геоида. Общеземной эллипсоид используют при решении глобальных геодезических задач, и в частности, при обработке спутниковых измерений. В настоящее время широко пользуются двумя общеземными эллипсоидами: ПЗ-90 (Параметры Земли 1990 г, Россия) и WGS-84 (Мировая геодезическая система 1984 г, США).

 Референц-эллипсоид – эллипсоид, принятый для геодезических работ в конкретной стране. С референц-эллипсоидом связана принятая в стране система координат. Параметры референц-эллипсоида подбираются под условием наилучшей аппроксимации данной части поверхности Земли. При этом совмещения центров эллипсоида и Земли не добиваются.

В России с 1946 г. в качестве референц-эллипсоида используется эллипсоид Красовского с параметрами: а = 6 378 245 м, a = 1/ 298,3.