Наблюдаемое значение критерия.
Для проверки нулевой гипотезы используют специально подобранную случайную величину, точное или приближенное распределение которой известно. Эту величину обозначают U или Z, если она распределена нормально, F или v2 - по закону Фишера-Снедекора, T - по закону Стьюдента, 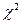 - по закону «хи квадрат» и т.д.
- по закону «хи квадрат» и т.д.
Например, если проверяют гипотезу о равенстве дисперсий двух нормальных генеральных совокупностей, то в качестве критерия принимают отношение их исправленных выборочных дисперсий:
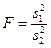 .
.
Эта величина случайная, она в различных опытах принимает различные наперед неизвестные значения, но известно, что она распределена по закону Фишера-Снедекора.
Для проверки гипотезы по данным выборок вычисляют частные значения входящих в критерий величин и в результате получают частное или наблюдаемое значение критерия.
О п р е д е л е н и е. Наблюдаемым значением называют значение критерия, вычисленное по выборкам.
Например, если по двум выборкам найдены исправленные выборочные дисперсии 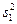 =20
=20 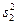 = 5, то наблюдаемое значение критерия F равно
= 5, то наблюдаемое значение критерия F равно
Fнабл = 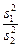 =
= 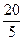 = 4.
= 4.
Критическая область. Область принятия гипотезы.
Критические точки.
После выбора определенного критерия множество его возможных значений разбивается на два непересекающихся подмножества, одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другое – при которых она принимается.
О п р е д е л е н и е. Критической областью называется совокупность значений критерия, при которых нулевая гипотеза отвергается.
О п р е д е л е н и е. Областью принятия гипотезы (или областью допустимых значений) называется совокупность значений критерия, при которых нулевая гипотеза принимается.
Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы – гипотезу принимают.
Поскольку критерий К – одномерная случайная величина, то все его возможные значения принадлежат некоторому интервалу. Поэтому критическая область и область принятия гипотезы также являются интервалами и, следовательно, есть точки, которые их разделяют.
О п р е д е л е н и е. Критическими точками kкр (иначе границами) называют точки, отделяющие критическую область от области принятия гипотезы.
Различают одностороннюю и двустороннюю критические области. В свою очередь односторонняя критическая область бывает правосторонней или левосторонне.
О п р е д е л е н и е. Правосторонней называют критическую область, определяемую неравенством 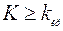 , где
, где 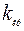 – положительное число.
– положительное число.
______________________________________
0 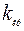
О п р е д е л е н и е. Левосторонней называют критическую область, определяемую неравенством 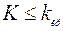 , где
, где 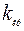 – отрицательное число.
– отрицательное число.
______________________________________
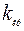 0
0
О п р е д е л е н и е. Односторонней называют правостороннюю или левостороннюю критическую область.
О п р е д е л е н и е. Двусторонней называют критическую область, определяемую неравенствами 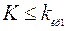 ,
, 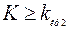 , где
, где 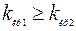 .
.
______________________________________
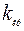 0
0 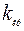
Если критические точки симметричны относительно нуля, то двусторонняя критическая область определяется неравенством 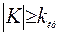 (в предположении, что
(в предположении, что 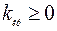 ).
).
Дата: 2019-02-02, просмотров: 375.