гипотез, ошибки первого и второго рода

О п р е д е л е н и е. Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений.

Например, статистическими являются следующие гипотезы:

1) генеральная совокупность распределена равномерно;

2) дисперсии двух нормально распределенных совокупностей равны меду собой.

В первой гипотезе сделано предположение о виде неизвестного распределения, во втором – о параметрах двух известных распределений.

Гипотеза «глобальное изменение климата на Земле произошло из-за столкновения Земли с крупным космическим объектом» не является статистической, так как в ней не идет речи ни о виде, ни о параметрах распределения.

Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то справедлива противоречащая ей гипотеза. Таким образом различают два вида гипотез.

О п р е д е л е н и е. Нулевой (или основной) называют выдвинутую гипотезу. Обозначают нулевую гипотезу Н₀ .

О п р е д е л е н и е. Конкурирующей (или альтернативной) называют гипотезу, противоречащую нулевой. Обозначают противоречащую гипотезу Н₁ .

Например, если нулевая гипотеза состоит в предположении, что математическое ожидание нормального распределения равно 10, a = 10, то конкурирующая гипотеза может состоять в предположении, что a 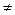10. Это записывается так: Н₀ : a = 10; Н₁: a 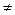10.

Также различают гипотезы по количеству предположений.

О п р е д е л е н и е. Простой называют гипотезу, содержащую только одно предположение.

Например, для показательного распределения гипотеза Н₀ : 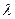 = 5 – простая. Или гипотеза Н₀ : для нормального распределения a = 3 (  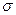известно) тоже простая.

О п р е д е л е н и е. Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.

Например, сложная гипотезе Н₀ : 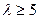 состоит из бесчисленного множества простых гипотез Н₀ :  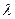= b, где b – любое число, больше 5.

Гипотеза Н₀ : для нормального распределения a = 3 ( 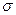 неизвестно) – сложная.

Выдвинутая гипотеза может быть правильной или неправильной. Поэтому возникает необходимость проверки гипотезы. Так как проверку осуществляют статистическими методами, то ее называют статистической проверкой.

В результате статистической проверки гипотезы возможно принятие неправильного решения, т.е. допущена ошибка. При этом возможна ошибка двух видов или говорят двух родов.

Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.

Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.

Вероятность совершить ошибку первого рода принято обозначать греческой буквой 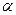. Ее называют уровнем значимости. Наиболее часто уровень значимости принимают равным 0,05 или 0,01. Это означает, что, если принять уровень значимости 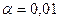, то в одном случае из ста имеется риск допустить ошибку первого рода – отвергнуть правильную гипотезу.