Ньютоновские жидкости – в этих жидкостях вязкость не зависит от градиента скорости. Они подчиняются уравнению Ньютона (вода, водные растворы, низкомолекулярные органические соединения ‑ этиловый спирт, ацетон).

Неньютоновские жидкости – это жидкости, для которых вязкость зависит от режима течения и градиента скорости. Это высокомолекулярные органические соединения, суспензии, эмульсии. Эти жидкости состоят из сложных и крупных молекул, которые могут образовывать пространственные структуры. Этот вид вязкости много больше, чем у ньютоновских жидкостей. Цельная кровь является неньютоновской жидкостью. Ее вязкость тем выше, чем медленнее она течет.

а) Течение крови в артериях в норме является ламинарным, т.е. упорядоченным. Ламинарное течение в переводе означает слоистое.

Рассмотрим ламинарное течение ньютоновской жидкости в трубе радиусом R и длиной L (рис. 8).

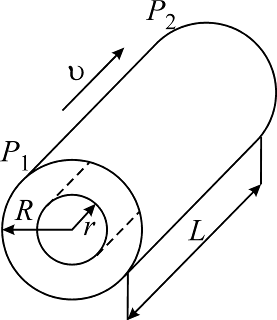
Рис. 8.

Для сохранения постоянного режима течения нужен перепад давлений (P₁-P₂). Выделим цилиндрический слой радиусом r. Течение жидкости в нем тормозится под действием силы трения, пропорциональной вязкости 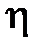 и площади боковой поверхности 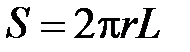, а также градиенту скорости 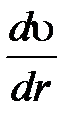; 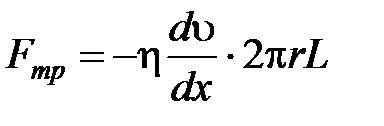. Силу трения можно найти через разность давлений:

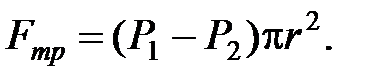
du = - Приравняем правые части выражений для F_тр и разделим переменные:  

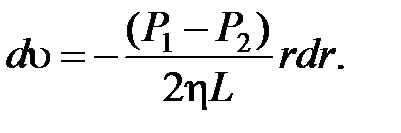
Проинтегрируем это выражение

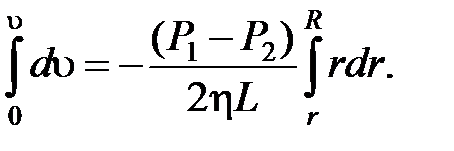
Поменяем местами пределы интегрирования для .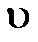

Получим следующее выражение для скорости:

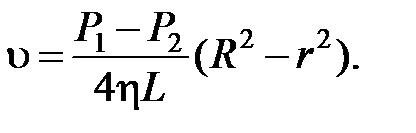
Это выражение показывает, что скорость от осевой линии до стенки трубы меняется по параболическому закону (рис. 9).

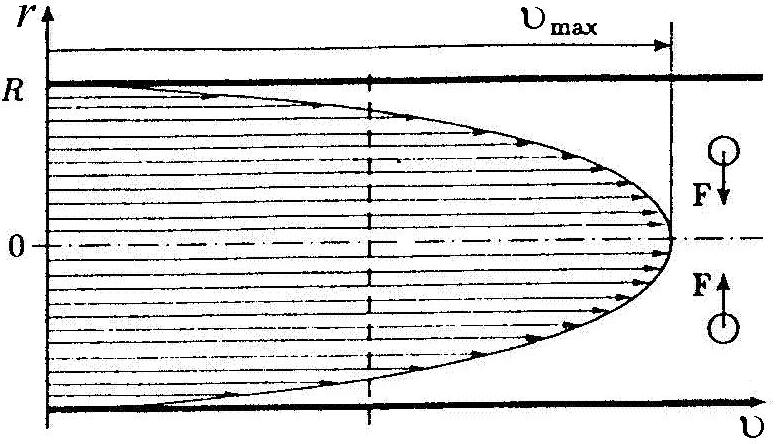
Рис. 9.

Низкая скорость около стенки означает, что давление здесь высокое в соответствие с уравнением Бернулли, в центре трубы минимальное. В связи с этим частицы (например, клетки крови) будут испытывать силу, толкающую их к центру трубы. По этой же причине клетки крови скапливаются вдоль оси потока, а плазма (малая вязкость) – по его периферии. Толщина плазмы составляет 0,004–0,04 мм. Эритроциты в этот слой практически не попадают. Плазма играет роль смазки, благодаря которой сопротивление движению эритроцитов снижается. Чем тоньше сосуд, тем более выражено снижение сопротивления.

б) Турбулентное течение – это хаотическое, крайне нерегулярное, неупорядоченное течение. Элементы жидкости совершают движение по сложным траекториям, что приводит к перемешиванию. При турбулентном течении эритроциты, которые обычно ориентированы своей длинной осью по направлению потока, переориентируются и располагаются хаотически. При таком движении местное изменение давления вызывает колебательное движение жидкости, которое сопровождается шумом. Турбулентное движение приводит к дополнительной работе сердца. Шум при турбулентности может быть использован для диагностирования заболевания. Шум прослушивается, например, на плечевой артерии при измерении давления крови.

Формула Пуазейля

Объем жидкости, протекающей по горизонтальной трубе радиуса R и длиной L ламинарно, можно вычислить следующим образом. Выделим в трубе тонкий цилиндрический слой радиусом r и толщиной dr (рис. 10).

Площадь его сечения 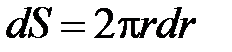. Т.к. слой тонкий, скорость жидкости в нем одинакова 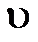. За единицу времени слой перенесет объем жидкости:

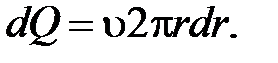
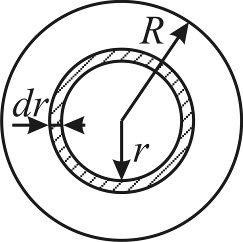
Рис. 10

Подставляя в это выражение 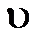 из формулы 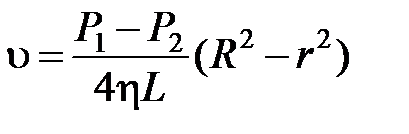, получим:

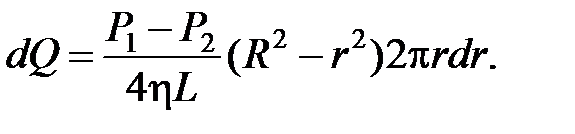
Интегрируем это выражение по всему сечению трубы:

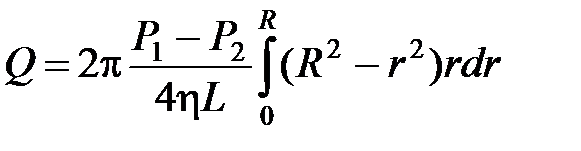
Окончательно: 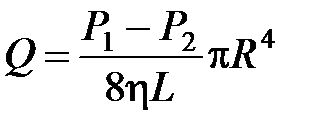 ‑ Формула Пуазейля для ньютоновских жидкостей.

Видно, что Q зависит от R⁴. Это очень сильная зависимость. Например, если при атеросклерозе радиус сосудов уменьшается в 2 раза, то для сохранения Q перепад давлений нужно увеличить в 16 раз. При этом сердце работает с перегрузкой. Скорость кровотока можно менять, изменяя вязкость крови, но вязкость зависит от температуры. С ростом температуры увеличивается скорость кровотока.

Закон Пуазейля используется при введении жидкостей с лечебной целью. Так, при подъеме камеры капельницы на высоту 120 см (вдвое выше стандартной) расход жидкости примерно удваивается, но при удвоении диаметра иглы поток жидкости должен возрасти в 16 раз. Для того чтобы добиться такого же увеличения скорости инъекции шприцем потребовалось бы 16-ти кратное увеличение силы.