Одной из наиболее важных задач, в которых используются определители, является решение систем n линейных уравнений с n неизвестными (n х n) .

Определение 1. Системой линейных уравнений (n х n) будем называть

Систему вида

Здесь x_j ( j =1,2,...,n) − неизвестные системы уравнений;

a_ij (i,j=1,2,..., n)− коэффициенты при неизвестных; b_i (i =1,2,...,n) − свободные члены системы уравнений. Из коэффициентов при неизвестных составим определитель

Этот определитель будем называть главным.

Составим ещё n определителей, каждый из которых получается из главного определителя ∆ заменой соответствующего столбца столбцом свободных членов.

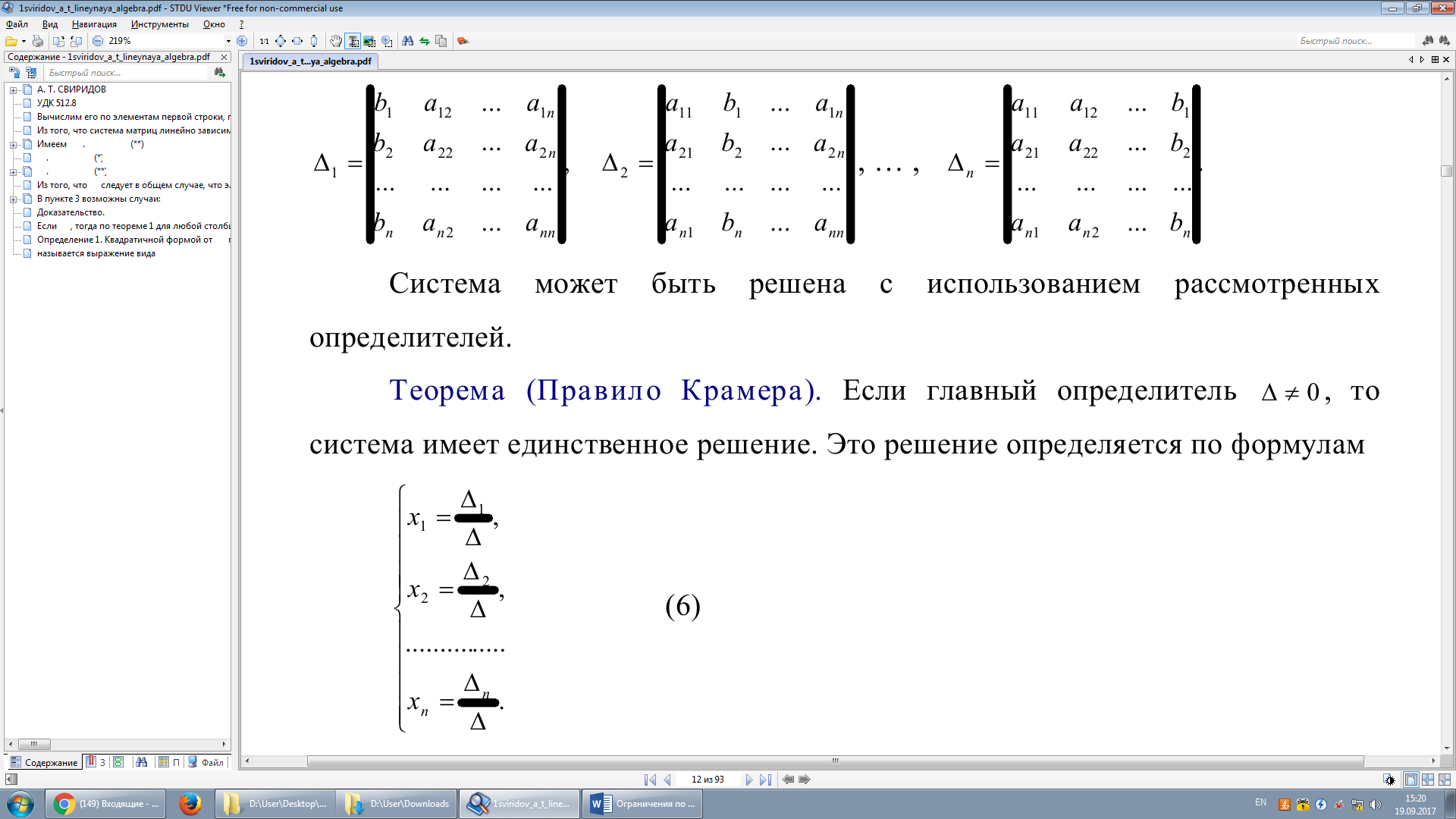
Система может быть решена с использованием рассмотренных определителей.

1. Теорема (Правило Крамера).

  Если главный определитель ∆ ≠ 0, то система имеет единственное решение. Это решение определяется по формулам

   Формула Крамера (6) очень важна в теоретическом отношении, так как позволяет найти явные выражения неизвестных через коэффициенты и свободные члены системы уравнений (5). Однако для решения системы линейных уравнений (5) с численными коэффициентами применять эти формулы нецелесообразно, особенно при больших n , так как это связано с громоздкостью вычислений определителей ∆ и ∆ j ( j = 1,2,...,n).

МАТРИЦЫ.

§ 1. Определение матриц. Общие понятия.

Определение 1. Матрицей размерностью (m х n) называется прямоугольная таблица чисел, состоящая из m строк и n столбцов.

 Матрицы обозначаются заглавными буквами.

Здесь a_ij элемент матрицы, стоящий на пересечении i − ой строки и j − го столбца. Для упрощения записи матрицы (1) будем записывать только его общий элемент, т. е.

Определение 2. Если в матрице А поменять местами строки с соответствующими столбцами, то получим матрицу, которая называется транспонированной по отношению к матрице А.

Транспонированную матрицу будем обозначать A' .

Или упрощённая запись A' = (a_ji ) . Из определения следует, что если матрица А имеет размерность (m х n), то размерность транспонированной матрицы A' будет (n х m) .

Из определений 1 и 2 следует, что повторное транспонирование приводит к исходной матрице, т. е. (A')' = A .

Определение 3. Если все элементы матрицы равны нулю, то такая матрица называется нулевой. Её упрощённая запись О = (0).

Определение 4. Если число строк матрицы равно числу столбцов, то

матрица называется квадратной. В этом случае число строк (столбцов)

Называется порядком квадратной матрицы.

 Определение 5. Если знаки у всех элементов матрицы А поменять  на противоположные, то полученная матрица называется противоположной относительно матрицы А и обозначается (-А).