Единицами измерения фазового сдвига являются радиан и градус:1° = π/180 рад.

В каталоговой классификации электронные измерители разности фаз и группового времени запаздывания обозначаются следующим образом: Ф1 — образцовые приборы, Ф2 — фазометры, ФЗ — измери­тельные фазовращатели, Ф4 — измерители группового времени запаз­дывания, Ф5 — измерители корреляции.

Электромеханические фазометры на лицевой панели имеют знак ∆φ.

Фаза характеризует состояние гармонического процесса в данный момент времени:

u(t) = U_m sin ( ω t + φ).

Фазой называется весь аргумент синусоидальной функции (ωt + φ). Обычно измерение ∆φ производится для колебаний одной и той же частоты:

u₁(t) = U_m sin (ω t + φ₁);

u₂(t) = U_m sin (ω t + φ₂).

В этом случае фазовый сдвиг

∆φ = (ωt + φ₁) - (ωt - φ₂) = φ₁ - φ₂ (5.10)

Для упрощения принимают начальную фазу одного колебания за нуль (например φ₂ = 0), тогда ∆φ = φ₁.

Приведенное понятие фазового сдвига относится только к гармо­ническим сигналам. Для негармонических (импульсных) сигналов применимо понятие временного сдвига (время задержки t₃),диаграм­мы которого приведены на рис. 5.6.

Рис.5.6. Диаграммы напряжений с временным сдвигом

Измерение фазового сдвига широко используется на промышлен­ных и сверхвысоких частотах, т.е. во всем диапазоне частот.

Фазовый сдвиг возникает, например, между входным и выходным напряжениями четырехполюсника, а также в силовых цепях перемен­ного тока между током и напряжением и определяет коэффициент мощности (cos φ), следовательно, и мощность в исследуемой цепи.

Для измерения фазового сдвига на промышленных частотах ши­роко используют электромеханические фазометры электродинамиче­ской и ферродинамической систем. Недостатками таких фазометров являются сравнительно большая потребляемая мощность от источни­ка сигнала и зависимость показаний от частоты. Относительная при­веденная погрешность электромеханических фазометров — не более ±0,5%.

В зависимости от требуемой точности измерения фазового сдвига и частоты сигнала применяют один из следующих методов: осциллографические (один из трех), компенсационный, электронный метод дискретного счета, метод преобразования фазового сдвига в импульсы тока, метод измерения с использованием фазометров на основе микро­процессорной системы, метод преобразования частоты сигнала.

Осциллографические методы, в свою очередь, разделяются на три: линейной развертки, синусоидальной развертки (эллипса) и кру­говой развертки.

Для реализации метода линейной развертки используют двухканальный или двухлучепой осциллограф (или однолучевой осцилло­граф с электронным коммутатором). На экране получается изображе­ние синусоидальных сигналов (рис. 5.7).

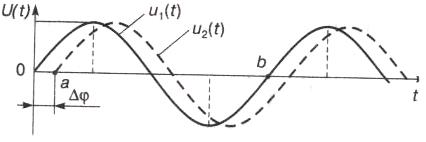
Рис.5.7. Осциллограммы двух синусоидальных сигналов при измерении фазового сдвига методом линейной развертки

Сигналы u₁(t)и u₂(t)подаются на входы Y1 и Y2 осциллографа. Для обеспечения неподвижности осциллограмм необходимо синхро­низировать развертку одним из исследуемых сигналов.

По измеренным отрезкам 0a и 0b рассчитывается фазовый сдвиг из соотношения

,

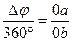откуда

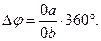(5.11)

Метод линейной развертки позволяет определить знак фазового сдвига, охватывает полный диапазон его измерения — 0...360°. Погреш­ность метода составляет ± (5...7°) и определяется нелинейностью раз­вертывающего напряжения, неточностью измерения линейных раз­меров отрезков 0а и 0b, качеством фокусировки и яркости луча (т.е. умением оператора).

Метод синусоидальной развертки реализуется с помощью одно; лучевого осциллографа. Исследуемые сигналы с напряжением u₁(t) и u₂(t) подаются на входы X и Y осциллографа при выключенном внутреннем генераторе линейной развертки. На экране появится фигура в виде эллипса (рис. 5.8), форма которого зависит от фазового сдвига между двумя напряжениями и их амплитуд. Фазовый сдвиг определяется по формуле

(5.12)

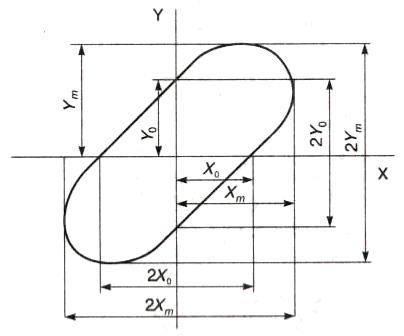
Рис.5.8. Результирующая осциллограмма при измерении фазового сдвига методом синусоидальной развёртки

Для уменьшения погрешности перед измерением выравнивают ам­плитуды Х_т и Y_m плавным их регулированием по каналам Y и X.

Метод синусоидальной развертки позволяет измерять фазовый сдвиг в пределах от 0...180° без определения знака.

Погрешность измерения ∆φ методом синусоидальной развертки (методом эллипса) зависит от точности измерения отрезков, входя­щих в уравнение (5.12), от качества фокусировки и яркости луча на экране ЭЛТ. Эти причины оказывают заметное влияние при фазовом сдвиге, близком к нулю и к 90°.

Оба рассмотренных метода являются косвенными и достаточно трудоемкими.

Метод круговой развертки — наиболее удобный осциллографический метод измерения фазового сдвига. При этом определяется знак фазового сдвига во всем диапазоне измерения угла (0...360°). Погреш­ность измерения постоянна во всем диапазоне.

На входы X и Y осциллографа подаются синусоидальные сигналы с на­пряжением U₁ и U₃ , сдвинутые относительно друг друга на 90° с помощью фазовращателя, состоящего из резистора и конденсатора. При равенстве сопротивлений плеч амплитуды напряжений U₁ и U₃ также равны и на экране будет наблюдаться осциллограмма в виде круга (рис. 5.9, б).

Сравниваемые сигналы u₁(t) и u₂(t) подаются на входы двух оди­наковых формирователей, которые преобразуют синусоидальные напряжения в последовательность коротких однополярных импульсов с напряжением U₄ и U₅ (рис. 5.9, в) с крутыми фронтами. Начала им­пульсов совпадают с моментом перехода синусоид через ось времени при их возрастании. Сигналы с напряжением U₄ и U₅ поступают на ло­гическую схему ИЛИ, где суммируются, и на выходе появляется по­следовательность импульсов с напряжением U₆ , которые подаются на управляющий электрод (модулятор) трубки, управляя яркостью луча в точках 1 и 2, и на окружности в точках 1 и 2 наблюдаются точки по­вышенной яркости.

Фазовый сдвиг между сигналами происходит следующим образом (см. рис. 5.9, б). При измерении центр прозрачного транспортира со­вмещают с центром круга, полная длина окружности которого соот­ветствует 360°. За период Т исследуемых сигналов с напряжением U₁ и U₂ электронный луч описывает круг. Дугу между точками 1 и 2, дли­на которой равна некоторому углу α, луч описывает за время задержки этих сигналов: ∆t = ∆φТ / 360°, откуда α= ∆φ.

Абсолютная погрешность измерения методом круговой развертки достигает 2...5° и зависит от точности определения центра круга, точ­ности измерения фазового сдвига с помощью транспортира и от степе­ни идентичности порога срабатывания обоих формирователей.

Компенсационный метод (метод наложения) реализуется с помо­щью осциллографа. Схема метода приведена на рис. 5.10, а.

Рис. 5.10. Схема реализации компенсационного метода (а) и осциллограмма (6) при измерении фазового сдвига

Сигналы с напряжением U₁ и U₂ подаются на входы Y и X осцилло­графа, причем на вход Y — через градуированный фазовращатель, а на вход X подается непосредственно.

Фазовый сдвиг между исследуемыми напряжениями U₁ и U₂ опре­деляется путем изменения фазы сигнала с напряжением U₃ фазовра­щателем до тех пор, пока на экране не появится прямая наклонная ли­ния (рис. 5.10, б), что свидетельствует о равенстве фаз обоих сигналов. Определяемый фазовый сдвиг ∆φ отсчитывают по шкале фазовращателя относительно первичного положения, соответствующего поворо­ту фазы на 180°. Для уменьшения погрешности измерения необходимо произвести коррекцию фазовых сдвигов, создаваемых усилителями каналов вертикального и горизонтального отклонения луча осциллографа. Эта процедура осуществляется в той же последовательности, что и при измерении фазового сдвига метолом синусоидальной раз­вертки (см. рис. 5.8). В качестве индикатора нуля можно использовать электронный вольтметр.

Погрешность измерения компенсационным методом небольшая (0,2...0,5°) и определяется главным образом качеством градуировки фазовращателя.

Компенсационный метод применяют и в диапазоне СВЧ при измерении фазового сдвига, вносимого каким-либо элементом, допол­нительно включаемым в тракт СВЧ (фильтром, отрезком волновода).Структурная схема измерения фазового сдвига компенсационным методом представлена на рис. 5.11.

Рис. 5.11. Структурная схема измерения фазового сдвига в диапазоне СВЧ компенсационным метолом

Процесс измерения производится в следующем порядке. При от­ключенном исследуемом элементе Z СВЧ-тракт на выходе фазовра­щателя замыкают заглушкой накоротко. При включении генератора в тракте устанавливается стоячая волна. Поскольку минимум стоячей волны более резко выражен, чем максимум, то настройкой фазовра­щателя так перемещают узел стоячей волны относительно поперечной плоскости расположения зонда, чтобы выпрямительный прибор (миллиамперметр) показал минимум, и отмечают показания φ₁, фазовраща­теля. Затем между фазовращателем и заглушкой включают исследуемый элемент Z, создающий смещение узла напряжения стоячей волны, и снова фазовращателем добиваются минимального показания инди­катора, которое составит φ₂ при отсчете по шкале фазовращателя.

Фазовый сдвиг, вносимый исследуемым элементом Z в СВЧ-тракт, определяется по формуле

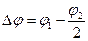(5.13)

Вместо фазовращателя и зонда в рассматриваемой схеме может быть использована измерительная линия. Описанный компенсацион­ный метод является косвенным.

Двухканальный фазометр позволяет измерить фазовый сдвиг непо­средственно. Принцип работы двухканального фазометра основан на преобразовании фазового сдвига в импульсы прямоугольной формы. Структурная схема двухканального фазометра, временные диаграммы сигналов, поясняющие его работу, и график зависимости показаний индикатора относительного ∆φ представлены на рис. 5.12.

Рис. 5.12. Структурная схема двухканального фазометра (а), временные диаграммы сигналов, поясняющие его работу (6) и график зависимости показаний индикатора относительно ∆φ (в)

Фазометр состоит из преобразователя ∆φ во временной сдвиг ∆t, равный искомому фазовому сдвигу ∆φ и измерительного индикатора. Преобразователь состоит из двух одинаковых формирователей сигна­ла и сумматора, в качестве которого используется триггер.

Исследуемые сигналы с напряжением U₁ и U₂ с фазовым сдвигом ∆φ подаются на входы двух одинаковых формирователей, которые преобразуют поступившие синусоидальные сигналы в последовательность коротких импульсов с напряжением U₃ и U₄. Импульсы с напряжени­ем U₃ запускают триггер, а импульсы с напряжением U₄ устанавливают его в исходное положение. В итоге на выходе образуется периодиче­ская последовательность импульсов, период повторения и длитель­ность которых равны периоду повторения T и сдвигу во времени ∆t исследуемых сигналов с амплитудой I_m .

В качестве измерительного индикатора чаще всего используется микроамперметр магнитоэлектрической системы, показания которого пропорциональны среднему значению силы тока за период повторе­ния сигнала Т.

Как видно из временной диаграммы I = f (t) (см. рис. 5.12, б), в цепи измерительного прибора получаются прямоугольные импульсы дли­тельностью ∆t. Следовательно, среднее за период значение силы тока, протекающего через приборы, пропорционально удвоенному относи­тельному временному интервалу:

откуда

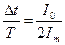(5.14)

Из графика (см. рис. 5.12, б) следует, что фазовый сдвиг между ис­следуемыми сигналами с напряжением U₁ и U₂ соответствует времен­ному сдвигу ∆t и может быть выражен формулой

из которой следует, что фазовый угол линейно зависит от отношения ∆t / T:

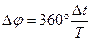(5.15)

Подставив уравнение (5.15) в выражение (5.14), получим

(5.16)

При постоянном значении амплитуды выходных импульсов шка­ла индикатора, измеряющего среднее значение силы тока I₀, градуи­руется в значениях ∆φ. При этом шкала индикатора фазометра будет линейной. Достоинством двухканального фазометра является прямое измерение ∆φ в диапазоне ±180°.

Электронный метод дискретного счета положен в основу ра­боты цифрового фазометра и состоит из двух основных этапов: пре­образование фазового сдвига в соответствующий интервал времени и измерение этого интервала времени методом дискретного счета.

Упрощенная структурная схема цифрового фазометра и временные диаграммы, поясняющие его работу, представлены на рис. 5.13.

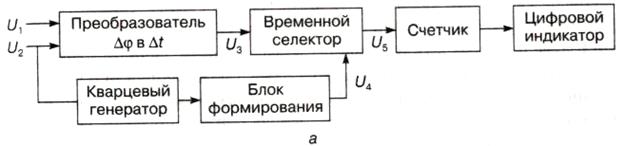
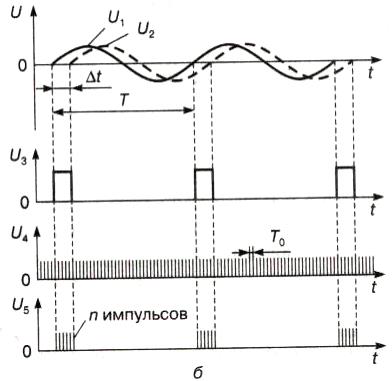
Рис. 5.13. Структурная схема фазометра при измерении фазового сдвига методом дискретного счета (а), и временные диаграммы сигналов, поясняющие его работу (б)

Вырабатываемый кварцевым генератором синусоидальный сигнал подается на блок формирования, на выходе которого образуются счет­ные импульсы, поступающие на один вход временного селектора. На другой его вход поступает преобразованная последовательность им­пульсов длительностью ∆t с периодом повторения исследуемых сиг­налов Т. Селектор открывается только на время, равное длительности ∆t импульсов с напряжением U₃ и пропускает на счетчик импульсы с напряжением U₄ от генератора. Временной селектор формирует па­кеты импульсов с напряжением U₅ (не изменяя периода Т), поступаю­щих на счетчик в одном пакете.

(5.17)

где T₀ — период повторения счетных импульсов кварцевого генератора.

Подставив в формулу (5.17) соотношение для ∆t из формулы (5.16), определяем ∆φ для сигналов с напряжением U₁ и U₂

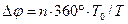(5.18)

Общая погрешность измерения этим методом зависит от погреш­ности дискретности, которая связана с тем, что интервал ∆t измеряется с точностью до одного периода Т₀ , и от нестабильности времени сраба­тывания преобразователя.

Большими возможностями обладают фазометры со встроенным микропроцессором, которыми можно измерять фазовый сдвиг между двумя периодическими сигналами за любой выбранный период.

На рисунке 5.14 представлена структурная схема фазометра co встроенным микропроцессором и временные диаграммы сигналов, поясняющие его работу.

После входного устройства синусоидальные сигналы с напряжением U₁ и U₂ поступают на входы импульсного преобразователя, в котором преобразуются в короткие импульсы с напряжением U '₁ и U '₂ С помощью первой пары данных импульсов формирователь 1 выра­батывает импульс с напряжением U₃ длительностью ∆t, которая равна временному сдвигу сигналов с напряжением U₁ и U₂. Этим импульсом открывается временной селектор 1, и в течение его действия на вход счетчика 1 проходят счетные импульсы с периодом повторения Т₀ , которые вырабатываются микропроцессором. Прошедший на вход счетчика 1 пакет импульсов с напряжением U₄ показан на рис. 5.14, б. Число импульсов в пакете выражается формулой

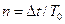(5.19)

Одновременно с этим формирователь 2 вырабатывает импульсы с напряжением U₅, с длительностью, равной периоду повторения иссле­дуемых сигналов с напряжением U₁ и U₂ . Этот импульс открывает се­лектор 2 (на время своего действия) и пропускает от микропроцессора на счетчик 2 пакет импульсов с напряжением U₆ и с периодом T₀ , число которых в пакете составляет

(5.20)

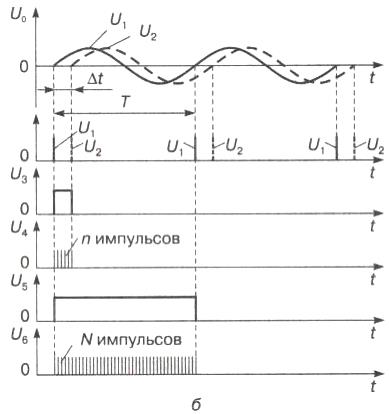
Рис. 5.14. Структурная схема фазометра со встроенным микропроцессором (а) и временные диаграммы сигналов, поясняющие его работу (б)

Для определения искомого значения фазового сдвига ∆φ за выб­ранный период повторения сигнала Т необходимо найти отношение величин (5.19) и (5.20), равное

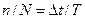
затем с учетом основной формулы ∆φ = 360° • ∆t / Т умножить это от­ношение на 360°:

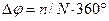(5.21)

Данное вычисление выполняется микропроцессором, на который передаются вырабатываемые счетчиками 1 и 2 коды чисел п и N. При соответствующей программе микропроцессора на дисплее высвечи­вается значение фазового сдвига ∆φ для любого выбранного периода Т. Благодаря сравнению таких сдвигов в разных периодах появляется возможность наблюдать флуктуации ∆φ и оценивать их статические параметры, к которым относятся математическое ожидание, диспер­сия, среднеквадратичное отклонение, измеренное среднее значение фазового сдвига.

При измерении фазометром со встроенным микропроцессором среднего значения фазового сдвига ∆φ за заданное количество К периодов Т в счетчиках 1 и 2 накапливаются коды числа импульсов, поступивших на их входы за К периодов, т.е. кодов чисел пК и NK соот­ветственно, передаваемых в микропроцессор.

Малую погрешность измерения ∆φ данным фазометром можно по­лучить только на достаточно низкой частоте исследуемых сигналов. Расширить частотный диапазон позволяет предварительное (гетеродинное) преобразование сигналов.

К основным метрологическим характеристикам фазометров, кото­рые необходимо знать при выборе прибора, относятся следующие:

· назначение прибора;

· диапазон измерения фазового сдвига;

· частотный диапазон;

· допустимая погрешность измерения.