Относительный показатель - это результат соотношения двух сопоставляемых абсолютных величин, выраженный в коэффициентах или процентах.

Выделяют следующие виды относительных величин:

Индекс планового задания – это отношение планового значения абсолютной величины к базисному:

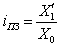
  Индекс выполнения плана – это отношение фактически полученного значения абсолютной величины в отчетном периоде к запланированному:

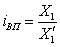
Перемножая индексы планового задания и выполнения плана, получим индекс динамики:

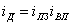
Индекс структуры (доля, удельный вес) - это отношение какой-либо части статистической совокупности к сумме всех ее частей:

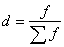
Индекс структуры показывает, какую долю составляет отдельная часть совокупности от всей совокупности.

   Индекс координации - это отношение одно части статистической совокупности к другой ее части, принятой за базу сравнения:

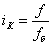
Индекс координации показывает, во сколько раз больше или сколько процентов составляет одна часть статистической совокупности по сравнению с другой ее частью, принятой за базу сравнения.

   Индекс сравнения - это отношение значений одной и той же абсолютной величины в одном и том же периоде или моменте времени, но для разных объектов или территорий:

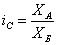
где А, Б — признаки сравниваемых объектов или территорий.

  Индекс интенсивности - это отношение значений двух взаимосвязанных абсолютных величин с разной размерностью, относящихся к одному объекту или явлению.

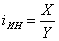
Средние величины и их виды

Средняя величина - это обобщающий показатель статистической совокупности, который погашает индивидуальные различия значений статистических величин, позволяя сравнивать разные совокупности между собой.

  Существует 2 класса средних величин: степенные и структурные .

К структурным средним относятся мода и медиана, но наиболее часто применяются степенные средние различных видов.

Степенные средние могут быть простыми и взвешенными.

  Средняя арифметическая - это самая часто используемая средняя величина, которая получается, если подставить в общую формулу m=1. Средняя арифметическая простая имеет следующий вид:

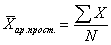
где X - значения величин, для которых необходимо рассчитать среднее значение; N - общее количество значений X (число единиц в изучаемой совокупности).

Средняя арифметическая взвешенная имеет следующий вид:

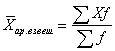
где f - количество величин с одинаковым значением X (частота).

     К наиболее часто используемым структурным средним относятся статистическая мода и статистическая медиана .

Статистическая мода - это наиболее часто повторяющееся значение величины X в статистической совокупности.

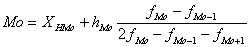
где Мо – мода;
Х_НМо – нижняя граница модального интервала;
h_Мо – размах модального интервала (разность между его верхней и нижней границей);
f_Мо – частота модального интервала;
f_Мо-1 – частота интервала, предшествующего модальному;
f_Мо+1 – частота интервала, следующего за модальным.

   Статистическая медиана – это значение величины X, которое делит упорядоченную по возрастанию или убыванию статистическую совокупность на 2 равных по численности части. В итоге у одной половины значение больше медианы, а у другой - меньше медианы.

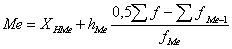
где Ме – медиана;
Х_НМе – нижняя граница медианного интервала;
h_Ме – размах медианного интервала (разность между его верхней и нижней границей);
f_Ме – частота медианного интервала;
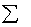f_Ме-1 – сумма частот интервалов, предшествующих медианному.