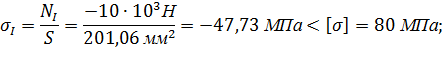
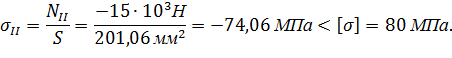
Условие выполняется.
Строим эпюру изменения напряжения растяжения (сжатия) по длине стержня под эпюрой продольной силы с соблюдением масштаба.
4. Определим абсолютную упругую деформацию стержня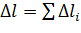 
, в нашем случае: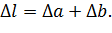 
Деформация на 1 участке:
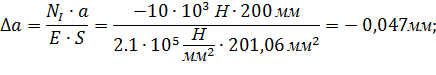
Деформация на 2 участке:
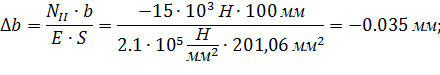
Таким образом, суммарная абсолютная упругая деформация равна:
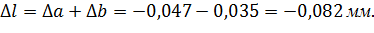
Ответ:
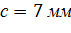
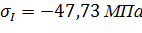
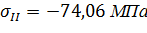
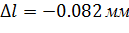
Задача №2 Расчет балки на прочность по нормальным напряжениям
Исходные данные:
| Наименование параметра | Значение | Единица измерения |
| P | 3 | кН |
| M | 6 | кН*м |
| q | 5 | кН/м |
| a | 2 | м |
| b | 4 | м |
| [s] | 120 | МПа |
| Форма сечения | прямоугольник | |
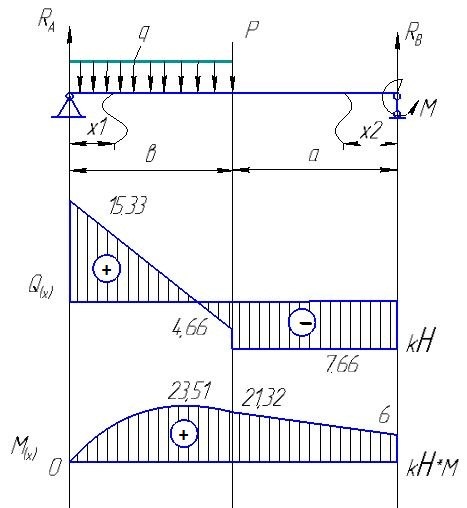
1. Обозначим реакции опор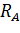 
и 
и 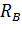определим их величину, используя уравнения равновесия для плоской системы сил:
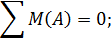
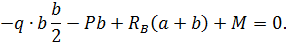
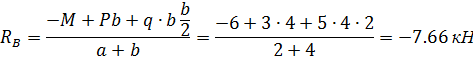
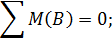
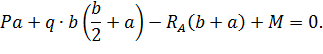
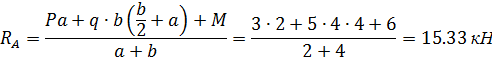
Проверка:
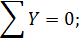
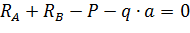
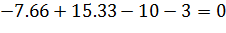
Реакции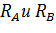 
определены верно.
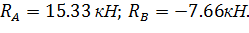
Обозначим участки слева направо I и II и сделаем два произвольных сечения.
2. Составим общие выражения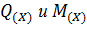 
по участкам I и II о определим их величину в соответствующим точках.
I участок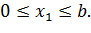 
На участке I поперечная сила определяется следующим образом:
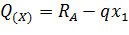
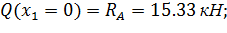
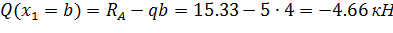
Уравнение изгибающего момента на I участке имеет вид:
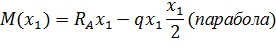
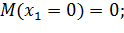
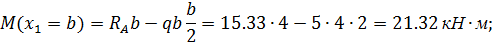
II участок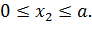 
На участке II поперечная сила определяется следующим образом:
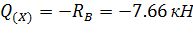
Строим эпюру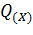 
Уравнение изгибающего момента на II участке имеет вид:
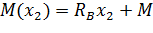
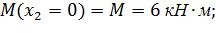
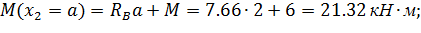
Найдем точку экстремума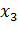 
:
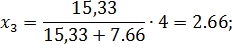
Строим эпюру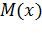 
3. Определяем размеры поперечного сечения, используя условие прочности:
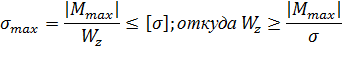
Из эпюры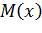 
видно, что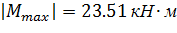 
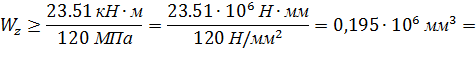
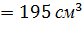
I случай: круглое сечение
Момент сопротивления сечения для круга
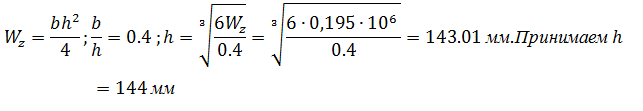
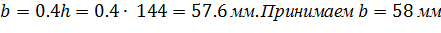
Определим погонную массу балки прямоугольного сечения:
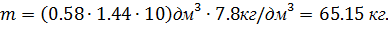
II случай: двутавр (ГОСТ 8239-72)
Выбираем двутавр, у которого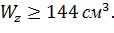 
Условию. Удовлетворяет двутавр №20, у которого 
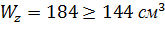и погонная масса составляет 21.0 кг. Использование балки двутаврового сечения позволяет снизить массу всей балки в 3 раза, по сравнению с прямоугольного сечения.
Задача №3 Расчет круглого прямого бруса (вала) на прочность и жесткость при кручении.
Исходные данные:
| Наименование параметра | Значение | Единица измерения |
| Т1 | 5 | кН*м |
| Т2 | 2 | кН*м |
| a | 1,7 | м |
| b | 3,4 | м |
| [t] | 80 | МПа |
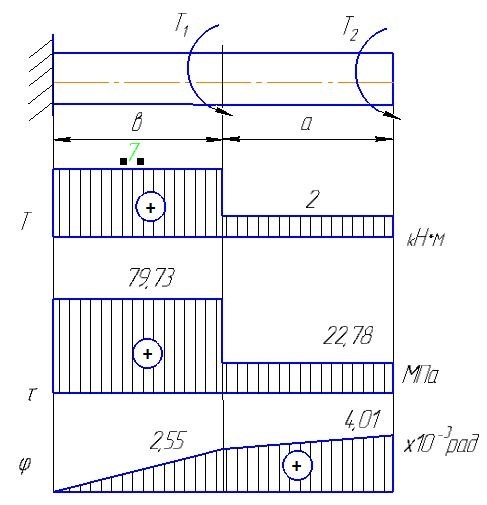
Обозначим участки слева направо I и II .
Определяем крутящие моменты на участках:
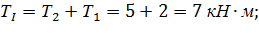
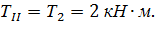
Строим эпюру крутящих моментов под расчетной схемой нагружения вала с соблюдением масштаба:
Из условия прочности на кручение
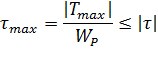
Определяем диаметр валов, приняв во внимание, что полярный момент сопротивления круга:
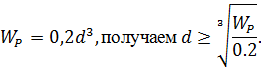
В нашем примере:
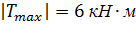
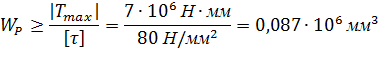
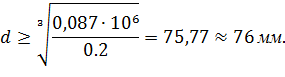
3. Определяем фактическое значение максимальных напряжений на участках:
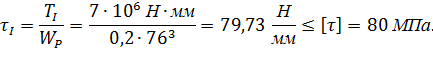
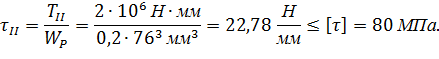
Дата: 2019-02-02, просмотров: 224.
