Задача №1 Расчет стержня при центральном растяжении или сжатии.
Исходные данные:
| Наименование параметра | Значение | Единица измерения |
| P1 | 5 | кН |
| P2 | 15 | кН |
| a | 0,2 | м |
| b | 0,1 | м |
| [s] | 80 | МПа |
| Форма сечения | круг | |
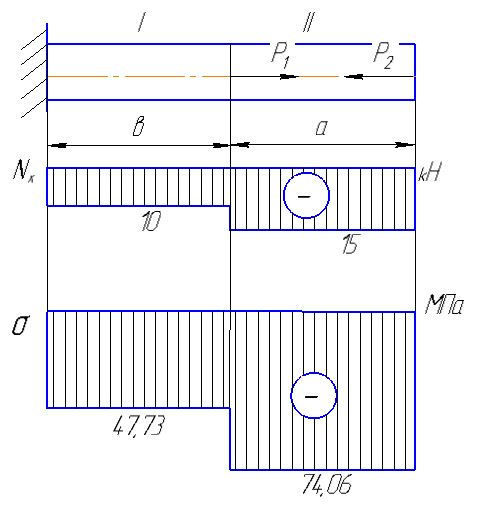
Стержень закреплен жёстко одним концом и к нему приложены две внешние силы Р1 и Р2, направление которых и точки их приложения совпадают с продольной осью стержня.
Стержень состоит из двух участков. Обозначим их, начиная с закрепленного конца, цифрами I и II.
1. Проведём на участке I произвольное сечение и рассмотрим равновесие правой отсеченной части:
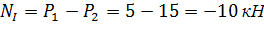
Знак перед числом говорит о том, что участок испытывает деформацию сжатия.
Проведем произвольное сечение на участке II. Определим нормальную (продольную) силу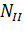 
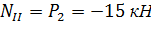
Данный участок испытывает деформацию растяжения.
Строим эпюру изменения продольной силы N(x) по длине стержня под расчетной схемой с соблюдением масштаба.
2. Определим размеры поперечного сечения из условия прочности при растяжении (сжатии):
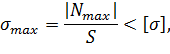
откуда следует:
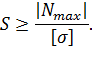
Из эпюры продольной силы видно, что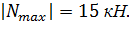 
Следовательно,
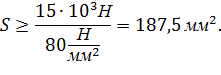
Принимая из условия задачи, что сечение - круг, определяем его стороны: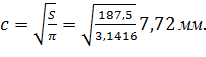 
Округляем в сторону увеличения до целого числа, т.е. принимаем с= 8мм. Тогда площадь поперечного сечения стержня будет равна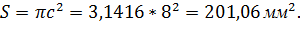 
Определим напряжения в поперечных сечениях стержня на обоих участках:
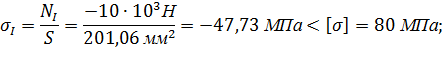
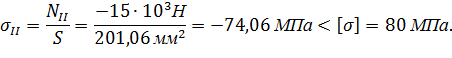
Условие выполняется.
Строим эпюру изменения напряжения растяжения (сжатия) по длине стержня под эпюрой продольной силы с соблюдением масштаба.
4. Определим абсолютную упругую деформацию стержня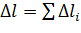 
, в нашем случае: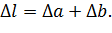 
Деформация на 1 участке:
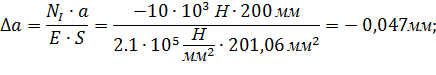
Деформация на 2 участке:
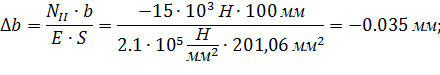
Таким образом, суммарная абсолютная упругая деформация равна:
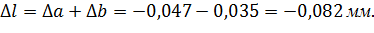
Ответ:
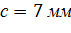
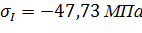
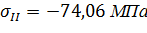
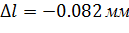
Задача №2 Расчет балки на прочность по нормальным напряжениям
Исходные данные:
| Наименование параметра | Значение | Единица измерения |
| P | 3 | кН |
| M | 6 | кН*м |
| q | 5 | кН/м |
| a | 2 | м |
| b | 4 | м |
| [s] | 120 | МПа |
| Форма сечения | прямоугольник | |
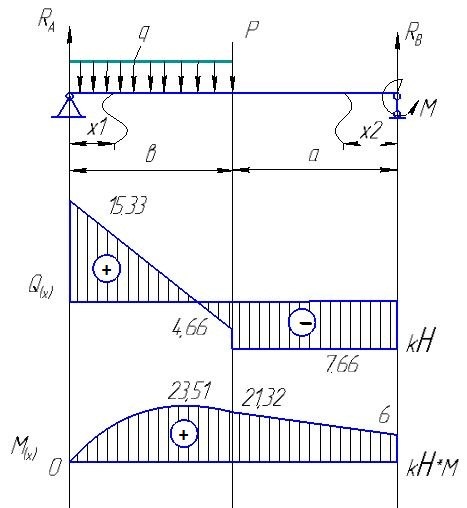
1. Обозначим реакции опор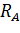 
и 
и 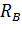определим их величину, используя уравнения равновесия для плоской системы сил:
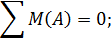
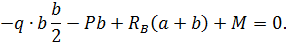
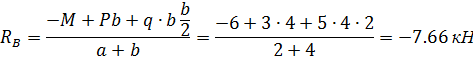
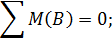
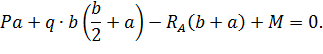
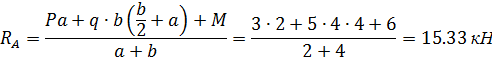
Проверка:
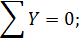
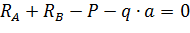
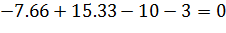
Реакции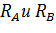 
определены верно.
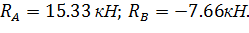
Обозначим участки слева направо I и II и сделаем два произвольных сечения.
2. Составим общие выражения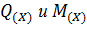 
по участкам I и II о определим их величину в соответствующим точках.
I участок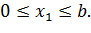 
На участке I поперечная сила определяется следующим образом:
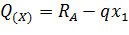
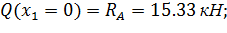
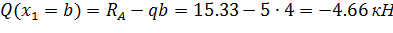
Уравнение изгибающего момента на I участке имеет вид:
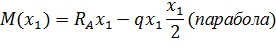
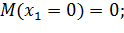
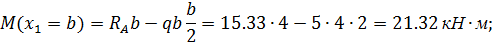
II участок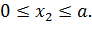 
На участке II поперечная сила определяется следующим образом:
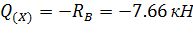
Строим эпюру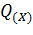 
Уравнение изгибающего момента на II участке имеет вид:
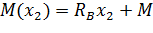
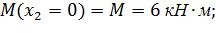
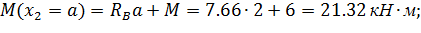
Найдем точку экстремума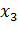 
:
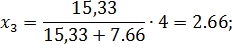
Строим эпюру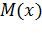 
3. Определяем размеры поперечного сечения, используя условие прочности:
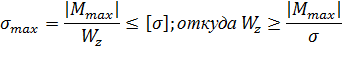
Из эпюры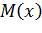 
видно, что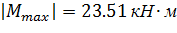 
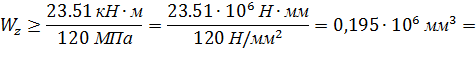
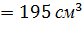
I случай: круглое сечение
Задача №1 Расчет стержня при центральном растяжении или сжатии.
Исходные данные:
| Наименование параметра | Значение | Единица измерения |
| P1 | 5 | кН |
| P2 | 15 | кН |
| a | 0,2 | м |
| b | 0,1 | м |
| [s] | 80 | МПа |
| Форма сечения | круг | |
Стержень закреплен жёстко одним концом и к нему приложены две внешние силы Р1 и Р2, направление которых и точки их приложения совпадают с продольной осью стержня.
Стержень состоит из двух участков. Обозначим их, начиная с закрепленного конца, цифрами I и II.
1. Проведём на участке I произвольное сечение и рассмотрим равновесие правой отсеченной части:
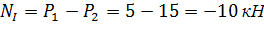
Знак перед числом говорит о том, что участок испытывает деформацию сжатия.
Проведем произвольное сечение на участке II. Определим нормальную (продольную) силу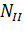
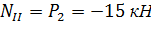
Данный участок испытывает деформацию растяжения.
Строим эпюру изменения продольной силы N(x) по длине стержня под расчетной схемой с соблюдением масштаба.
2. Определим размеры поперечного сечения из условия прочности при растяжении (сжатии):
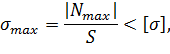
откуда следует:
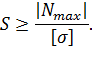
Из эпюры продольной силы видно, что 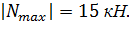Следовательно,
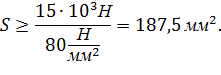
Принимая из условия задачи, что сечение - круг, определяем его стороны: 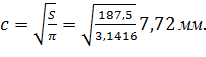Округляем в сторону увеличения до целого числа, т.е. принимаем с= 8мм. Тогда площадь поперечного сечения стержня будет равна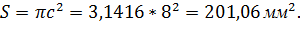
Дата: 2019-02-02, просмотров: 263.
