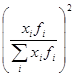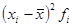Показатели дифференциации и концентрации

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Анализ вариации в рядах распределения целесообразно дополнить показателями дифференциации.

Для оценки дифференциации значений признака ряда используются децильный коэффициент дифференциации и коэффициент фондов.

Децильный коэффициент равен отношению девятой децили к первой децили. Децильный коэффициент широко применяют при измерении соотношения уровней дохода 10% наиболее обеспеченного и 10% наименее обеспеченного населения (в разах).

Коэффициент фондов равен отношению среднего уровня 10-й децили к среднему уровню 1-й децили. Он дает более точный уровень дифференциации.

Государственная статистика регулярно публикует коэффициент фондов для характеристики дифференциации доходов. Однако в исследовательской работе чаще используется децильный коэффициент дифференциации. Его применение особенно эффективно в случае, если, например, в распределении доходов в начале первого дециля присутствуют крайне низкие доходы, а десятый дециль завершается аномально высокими доходами, которые существенно влияют на сумму доходов в этих децилях. В такой ситуации правильнее применять децильный коэффициент дифференциации, а не коэффициент фондов.

К показателям дифференциации близки по значению показатели концентрации: коэффициент Джини и коэффициент Герфиндаля.

Коэффициент концентрации Джини рассчитывается по формуле:

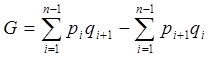, (6.27)

где p_i – накопленная доля (частость) численности единиц ряда

q_i – накопленная доля значений признака, приходящаяся на все единицы ряда со значеними признака не более x_i_.[2]

Коэффициент Джини может принимать значения от 0 до 1, поэтому результат следует разделить либо на 100, если p_i или q_i выражен в процентах, либо на 10000, если оба показателя выражены в процентах. Чем больше концентрация признака, тем ближе коэффициент Джини к 1. Коэффициент Джини используют для характеристики степени неравномерности распределения совокупности (например, населения) по уровню признака (например, доходов).

Коэффициент Герфиндаля вычисляется на основе данных о доле изучаемого признака в i-той группе в совокупном объеме признака:

или , (6.28)

где – доля выручки i-той группы в общем объеме всех значений признака;

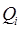– объём значений признака в i -той группе.

Показатель Н зависит от числа единиц в группах.

Пример 6.6. Имеются данные о полученной балансовой прибыли 50 крупнейших банков России (по состоянию на 01.01.1998 г.) (в млн. руб.):

1	-	974,2	11	-	188,8	21	-	143,9	31	-	85,4	41	-	69,3
2	-	609,2	12	-	187,3	22	-	134,6	32	-	84,5	42	-	66,4
3	-	588,3	13	-	186,8	23	-	120,9	33	-	82,4	43	-	66,2
4	-	562,9	14	-	171,1	24	-	112,2	34	-	79,6	44	-	59,7
5	-	436,3	15	-	167,9	25	-	108,5	35	-	74,3	45	-	59,1
6	-	432,5	16	-	164,3	26	-	101,6	36	-	74,0	46	-	58,3
7	-	283,6	17	-	160,3	27	-	101,3	37	-	73,5	47	-	57,4
8	-	265,8	18	-	159,9	28	-	97,4	38	-	73,2	48	-	53,8
9	-	231,5	19	-	157,5	29	-	97,4	39	-	73,0	49	-	51,4
10	-	211,7	20	-	147,6	30	-	92,0	40	-	71,5	50	-	51,2

Величина балансовой прибыли Сбербанка России на 01.07.97 – 4353,283 млн. руб.

1. Постройте вариационный ряд, образовав 7-8 интервалов произвольно.

2. Рассчитайте средний размер балансовой прибыли на один банк на основе средней арифметической, моды и медианы.

3. Рассчитайте показатели вариации.

4. Измерьте дифференциацию банков на основе децильного коэффициента и коэффициента фондов.

5. Рассчитайте коэффициент концентрации Джини и Герфиндаля.

Решение:

1. Распределение 50 банков РФ по размеру балансовой прибыли (БП) на 01.01.1998 г.

БП, млн. руб. x_k _-1 - x_k	Коли-чество банков		Сере-дина интер- вала x_i	x_if_i	На-копл. час-тоты V_i, %	На-копл. час-тос- ти p_i	Доля БП групп банков в общем объеме БП
БП, млн. руб. x_k _-1 - x_k	f_i	в % к ито- гу	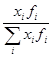Сере-дина интер- вала x_i	x_if_i	На-копл. час-тоты V_i, %	На-копл. час-тос- ти p_i		на- раст. ито- гом, q_i
А	1	2	3	4	5	6	7	8	9	10
50-60	7	14	55	385	7	14	0,042	0,042	0,02	116487
60-80	10	20	70	700	17	34	0,076	0,118	0,006	129960
80-100	6	12	90	540	23	46	0,059	0,177	0,003	53016
100-150	8	16	125	1000	31	62	0,109	0,286	0,012	27848
150-300	13	26	225	2925	44	88	0,318	0,604	0,101	21853
300-500	2	4	400	800	46	92	0,087	0,691	0,008	93312
500-800	3	6	650	1950	49	98	0,212	0,902	0,045	651468
800-1000	1	2	900	900	50	100	0,098	1,0	0,010	512656
Итого	50	100	-	9200	-	-	1	-	0,187	1606600

2. Средние показатели:

а) средний размер балансовой прибыли на один банк рассчитаем по средней арифметической взвешенной:

б) моду рассчитаем по формуле (5.6):

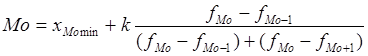Модальный интервал – 150-300, т.к. частота этого интервала, равная 13, является максимальной.

;

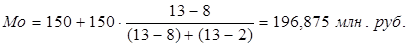в) медиану рассчитаем по формуле (5.5):

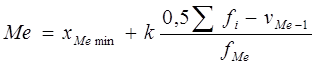Медианный интервал – 100-150, т.к. накопленная частота этого интервала, равная 31, - первая накопленная частота, превышающая половину суммы частот ряда.

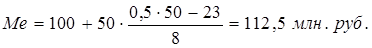
3. Показатели вариации:

а) дисперсия (по формуле 6.6):

= ;

б) среднее квадратическое отклонение (по формуле 6.7):

;

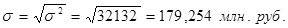в) коэффициент вариации (по формуле 6.11):

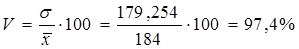
V >35%, что свидетельствует о неоднородности совокупности.

4. Показатели дифференциации:

а) для нахождения децильного коэффициента определим вначале первый и девятый децили по формуле 5.4:

Интервал, соответствующий первому децилю, – 50-60, т.к. накопленная частота этого интервала, равная 7, первая накопленная частота, превышающая 0,1 суммы частот.

Интервал, соответствующий девятому децилю, – 300-500, т.к. накопленная частота этого интервала, равная 14, первая накопленная частота, превышающая 0,9 суммы частот.

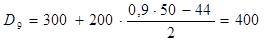
Тогда децильный коэффициент составит: ;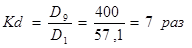

б) т.к. 10% самых крупных и 10% самых мелких банков составляют одну и ту же величину (в нашем примере 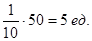), то фондовый коэффициент составит (по данным исходной таблицы):

5. Показатели концентрации:

а) коэффициент Джини рассчитаем по формуле 6.27, произведя предварительные расчеты


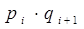
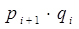
1,652	1,428
6,018	5,428
13,156	10,974
37,448	25,168
60,808	55,568
82,984	67,718
98	90,02

;

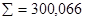
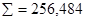
б) коэффициент Герфиндаля определим по формуле 6.28 (см. итог гр 9):

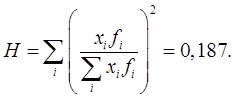Пример 6.7. Для иллюстрации принципа расчета коэффициентов Джини и Герфиндаля воспользуемся данными выборочного обследования дневной выручки 20 продуктовых магазинов (тыс. руб.):

Номера мага-зинов i	Значения признака (выручка магазина) х _i	Накоп-ленные значения признака	Накоп-ленная доля значений признака q_i	Накоп-ленная доля численности единиц ряда: p_i
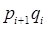
1	9	9	0,022	0,05	0,002	-	0,0005
2	9	18	0,044	0,1	0,007	0,002	0,0005
3	11	29	0,071	0,15	0,014	0,007	0,0007
4	12	41	0,1	0,2	0,025	0,015	0,0009
5	15	56	0,137	0,25	0,041	0,027	0,0013
6	16	72	0,176	0,3	0,062	0,044	0,0015
7	17	89	0,218	0,35	0,087	0,065	0,0017
8	18	107	0,262	0,4	0,118	0,092	0,0019
9	19	126	0,308	0,45	0,154	0,123	0,0021
10	21	147	0,359	0,5	0,198	0,162	0,0026
11	21	168	0,411	0,55	0,246	0,205	0,0026
12	25	193	0,472	0,6	0,307	0,296	0,0037
13	25	218	0,533	0,65	0,373	0,320	0,0037
14	26	244	0,597	0,7	0,447	0,388	0,0040
15	26	270	0,66	0,75	0,528	0,462	0,0040
16	26	296	0,724	0,8	0,615	0,543	0,0040
17	26	322	0,787	0,85	0,709	0,630	0,0040
18	27	349	0,853	0,9	0,811	0,725	0,0044
19	30	379	0,927	0,95	0,927	0,834	0,0054
20	30	409	1,0	1,0	-	0,95	0,0054
å					5,670	5,584	0,05528

Коэффициент Джини равен 0,086, что свидетельствует о невысоком уровне концентрации выручки магазинов. Значение коэффициента Герфиндаля, равное 0,05528, подтверждает этот вывод.

Следует отметить, что приведенные расчеты носят исключительно иллюстративный характер, поскольку экономический смысл коэффициентов Джини и Герфиндаля наиболее полно проявляется лишь при проведении сравнений исследуемых явлений во времени и в пространстве. Например, коэффициента Джини для характеристики дифференциации доходов населения в различных регионах РФ или странах, коэффициента Герфиндаля для характеристики концентрации производства, капитала. Основное достоинство коэффициента Герфиндаля – его высокая чувствительность к изменению в суммарном обороте долей крупнейших участников, что позволяет отслеживать концентрацию рыночного оборота и реагирует на число участников рынка. Коэффициент Герфиндаля может быть использован в качестве меры диверсификации кредитного портфеля банка. Чем меньше значение коэффициента Герфиндаля, т.е. чем больше диверсифицирован кредитный портфель, тем ниже могут быть требования по капиталу к кредитному портфелю.

6.2. Контрольные вопросы к теме 6

1. Чем вызвана необходимость изучения вариации признака?

2. Укажите основные показатели вариации.

3. Какие вам известны способы расчета дисперсии и среднего квадратического отклонения?

4. Как определяется дисперсия альтернативного признака?

5. Что такое коэффициент вариации?

6. Правило сложения дисперсий. Что показывают частная (внутригрупповая), средняя из частных, межгрупповая и общая дисперсии?

7. Как рассчитываются и что характеризуют коэффициент детерминации и эмпирическое корреляционное отношение?

8. Как рассчитывают и что характеризуют коэффициент дифференциации и коэффициент фондов?

9. Показатели концентрации: коэффициенты Джини и Герфиндаля.

6.3. Контрольные задания к теме 6

1. Дисперсия признака равна 600. Объем совокупности равен 10. Сумма квадратов индивидуальных значений признака равна 6250. Найти среднюю величину.

2. Средняя величина в совокупности равна 15, среднее квадратическое отклонение равно 10. Чему равен средний квадрат индивидуальных значений этого признака?

3. Средняя величина в совокупности равна 13, а средний квадрат индивидуальных значений этого признака равен 174. Определить коэффициент вариации.

4. Дисперсия признака равна 360000, коэффициент вариации равен 50%. Чему равна средняя величина признака?

5. Дисперсия признака равна 360, средний квадрат индивидуальных значений равен 585. Чему равна средняя?

6. Определить дисперсию признака, если средняя величина признака равна 2600, а коэффициент вариации признака равен 30%.

7. Общая дисперсия равна 8,4. Средняя величина признака для всей совокупности равна 13. Средние по группам равны соответственно 10, 15 и 12. Численность единиц в каждой группе составляет 32, 53 и 45. Определить среднюю внутригрупповую дисперсию.

8. По совокупности, состоящей из 100 единиц, известны: средняя арифметическая – 47,0; сумма квадратов индивидуальных значений признака – 231592. Определить, однородна ли изучаемая совокупность.

9. Определить величину эмпирического корреляционного отношения, если общая дисперсия равна 15,2; групповые средние ; 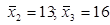, а численность групп соответственно равна 75, 60 и 65.

10. Для изучения уровня заработной платы рабочих на предприятии обследовано 500 мужчин и 300 женщин. Результаты исследования показали, что у мужчин средняя заработная плата составила 1200 у.е. при среднеквадратическом отклонении 200 у.е., у женщин соответственно 800 у.е. и 150 у.е.

Определить: 1) среднюю заработную плату работников;

2) дисперсии заработной платы и коэффициент вариации;

3) коэффициент детерминации и эмпирическое корреляционное отношение.

11. Имеются данные о чистой прибыли (балансовой за вычетом налогов) предприятий двух районов:

Район	Число предприятий	Чистая прибыль, млн. руб.
1	6	4, 6, 9, 4, 7, 6
2	10	8, 12, 8, 9, 6, 5, 7, 7, 8, 10

Определите дисперсии чистой прибыли: групповые (по каждому району), среднюю из групповых, межгрупповую и общую.

12. Имеются данные о заработной плате по двум группам работников:

Группы работников	Число работников	Заработная плата, у.е
Работающие в 1-й фирме	4	200
	2	300
	1	400
Работающие в 2-х фирмах	3	500
Работающие в 2-х фирмах	2	600

Найти все виды дисперсий заработной платы, коэффициент детерминации и эмпирическое корреляционное отношение.

13. Имеются следующие данные о среднем ежедневном времени занятости семейных женщин в домашнем хозяйстве:

Возрастные группы семейных женщин в домашнем хозяйстве	Численность женщин в группе	Частные средние (часов в день)	Частные дисперсии
до 25	250	2,0	4,0
25-45	420	3,5	6,8
свыше 45	330	3,2	5,0

Найти общую дисперсию занятости, коэффициент детерминации и эмпирическое корреляционное отношение.

14. Есть две группы людей с разным месячным доходом (тыс. руб.):

Группа А: 3, 3, 3, 4.

Группа Б: 6, 6, 7.

В какую группу нужно отнести человека с доходом 5 тыс. руб. в месяц?

15. По результатам маркетингового исследования туристических фирм, организующих недельные туры в Турцию в различные курортные города, получены следующие данные о вариации стоимости туров (цены приведены для гостиниц одного класса):

Месторасположение курорта	Число туристических фирм	Средняя цена недельного тура, у.е.	Дисперсия цен тура в группе
Анталия	7	530	2720
Бодрум	6	590	8855
Итого	13	550	5550

Найти общую дисперсию, коэффициент детерминации и эмпирическое корреляционное отношение.

16. По данным выборочного обследования заработной платы работников бюджетной сферы получены следующие показатели:

Отрасль	Средняя заработная плата, руб.	Численность работников, чел.	Дисперсия заработной платы
здравоохранение	600	80	4900
образование	800	120	16900

Определить: 1) среднюю заработную плату работников по двум отраслям;

2) дисперсии заработной платы;

3) коэффициент детерминации и эмпирическое корреляционное отношение.

17. Имеются следующие данные (условные) по трем группам рабочих:

Стаж работы (лет)	Число рабочих	Средняя заработная плата, руб.	Среднеквадратическое отклонение заработной платы
до 3	10	500	12
3 –10	15	600	10
более 10	25	700	20

Рассчитать: 1) среднюю заработную плату всей совокупности рабочих;

2) дисперсии заработной платы;

3) коэффициент детерминации и эмпирическое корреляционное отношение.

18. При изучении бюджета времени студентов было проведено обследование учащихся вузов. При обследовании вузы были разбиты на 7 групп по специализации. Были получены следующие результаты среднего количества времени, затрачиваемого студентами ежедневно на самостоятельную работу:

вузы по группам специальностей	Число обследованных студентов, тыс.чел.	Среднее число часов на самостоятельную работу	Средний квадрат отклонений
Промышленность и строительство	42	2,0	0,6
Транспорт	5	1,4	0,5
Право	13	1,7	0,3
Экономика	22	1,5	0,7
Здравоохранение	10	1,0	0,8
Искусство	5	1,6	1,0
Просвещение	36	1,8	0,.6

Используя правило сложения дисперсий, определить зависимость между средним числом часов на самостоятельную работу от специализации студента.

19. Для определения средней величины расходов на полугодовую подписку на газеты и журналы обследуемая совокупность семей разбита на группы по уровням дохода на три группы. По группам получены следующие результаты:

Номер группы	Число семей в группе	Средние расходы на подписку, руб.	Групповые дисперсии
1	300	200	14
2	500	400	30
3	200	600	60

Определите все виды дисперсий расходов, коэффициент детерминации и эмпирическое корреляционное отношение.

20. В районе 20 тыс. семей, проживающих в городах, поселках городского типа и сельской местности. В результате были получены следующие данные о среднем числе детей в семьях:

Семьи, проживающие	Удельный вес семей в генеральной совокупности, %	Среднее число детей в семьях	Среднее квадратическое отклонение
В городах	50	2,3	1,2
В пос. гор. типа	10	1,8	0,5
В сельской местности	40	2,8	2,5

Используя правило сложения дисперсий, определите коэффициент детерминации и эмпирическое корреляционное отношение.

21. Имеются следующие выборочные данные о вкладах населения района:

Группы населения	Число вкладов	Средний размер вклада, тыс. руб.	Коэффициент вариации вклада, %
Городское	7	4	20
Сельское	3	6	30

Определите тесноту связи между средним размером вклада и типом населения, исчислив коэффициент детерминации и эмпирическое корреляционное отношение.

22. Капитал коммерческих банков характеризуется следующими данными:

№ п/п	Собственный капитал банков, млн. руб.	Число банков	Средний размер привлеченных средств (капитала), млрд. руб.	Дисперсия привлеченных средств
1	30-40	8	100	400
2	40-50	10	180	2500
3	50-60	2	200	3600

Определите показатели тесноты связи между размером собственного капитала банков и привлеченными средствами, исчислив коэффициент детерминации и эмпирическое корреляционное отношение.

23. По данным обследования коммерческих банков города 70% общего числа клиентов составили юридические лица со средним размером кредита 120 тыс. руб. и коэффициентом вариации 25%, а 30% – физические лица со средним размером ссуды 20 тыс. руб. при среднем квадратическом отклонении 6 тыс. руб.

Используя правило сложения дисперсий, определите тесноту связи между размером кредита и типом клиента, исчислив коэффициент детерминации и эмпирическое корреляционное отношение.

24. Товарооборот по предприятиям общественного питания на одного работника за квартал характеризуется следующими данными:

Предприятие	Доля предприятий в общей численности работников, %	Товарооборот в расчете на одного работника, тыс. руб.	Дисперсия товарооборота в группе
Столовые	35	13	3,29
Кафе, закусочные	50	20	36,00
Рестораны	15	26	9,00

Определите все виды дисперсий товарооборота предприятий общественного питания, коэффициент детерминации и эмпирическое корреляционное отношение.

25. Имеются данные о распределении семей сотрудников финансовой корпорации по количеству детей:

Число детей	Число семей сотрудников по подразделениям
в семье	первое	второе	третье
0	4	7	5
1	6	10	13
2	3	3	3
3	2	1	-

Вычислите все виды дисперсий, используя правило сложения дисперсий.

26. Распределение основных фондов по малым предприятиям отрасли характеризуется следующими данными:

Группы предприятий по стоимости основных фондов, тыс. руб.	Число предприятий	Основные фонды в среднем на предприятии, тыс. руб.	Групповые дисперсии
12-27	18	18	1,14
27-42	40	32	1,09
42-57	26	48	1,69
57-72	12	69	1,84

Рассчитайте коэффициент детерминации и эмпирическое корреляционное отношение. Сделайте выводы.

27. По переписи населения 1926 года в России доля грамотных среди женщин составляла 46%, а среди мужчин – 77%. Определить общий (средний) процент грамотности всего населения и дисперсию этого показателя, если женщины составляли 53% в общей численности населения.

28. Определить дисперсию и среднее квадратическое отклонение, если при проверке партии изделий из 1000 шт. 30 шт. оказались бракованными.

29. Для определения удельного веса женщин в численности работающих в отрасли все предприятия были разбиты по среднесписочному числу работающих на 3 группы:

1-я гр. – с числом работающих до 1000 человек;

2-я гр. – с числом работающих от 1001 до 5000 человек;

3-я гр. – с числом работающих свыше 5000 человек.

Общая численность работающих в 1 группе – 120 тыс.человек, во 2-й группе – 89 тыс., в 3-й группе – 50 тыс. Доля женщин в первой группе оказалась равной 47%, во 2-й – 36%, в 3-й – 29%. С помощью правила сложения дисперсий определите дисперсию удельного веса женщин в отрасли.

30. Имеются следующие данные о числе домохозяйств, находящихся в условиях крайней бедности (среднедушевые доходы в два раза ниже прожиточного минимума):

Домохозяйство	Обследовано домохозяйств	Доля домохозяйств, находящихся в крайней бедности, %
Без детей	200	6
С детьми в возрасте до 16 лет	500	18
Пенсионеров	100	25

Определите все виды дисперсий, коэффициент детерминации и эмпирическое корреляционное отношение. Сделайте выводы.

31. Имеются следующие данные о расходах домохозяйств района на товары культурно-бытового назначения:

Домохозяйство	Обследовано домохозяйств	Доля расходов на товары культурно-бытового назначения, %
Имеющие детей	400	9
Без детей	100	39

Определите все виды дисперсий, коэффициент детерминации и эмпирическое корреляционное отношение.

32. Имеются следующие данные о расходах на платные услуги домохозяйствами района:

Домохозяйства	Обследовано домохозяйств	Доля расходов на платные услуги, %
городских поселений	400	30
сельской местности	100	10

Определите все виды дисперсий, коэффициент детерминации и эмпирическое корреляционное отношение.

33. Имеются следующие выборочные данные о расходах на питание домохозяйствами города:

	Численность домохозяйств в выборке	Доля расходов на питание
Одинокие	30	42
Семейные	70	53

Определите все виды дисперсий, коэффициент детерминации и эмпирическое корреляционное отношение.

34. Имеются данные о совокупной выручке (млрд. руб.) за 1997г. 50 крупнейших аудиторско-консультационных фирм:

1	-	78,1	11	-	17,5	21	-	7,2	31	-	4,0	41	-	2,7
2	-	44,8	12	-	15,8	22	-	7,0	32	-	3,8	42	-	2,7
3	-	35,2	13	-	15,7	23	-	6,8	33	-	3,6	43	-	2,7
4	-	34,6	14	-	14,5	24	-	6,6	34	-	3,6	44	-	2,7
5	-	32,5	15	-	13,2	25	-	5,6	35	-	3,5	45	-	2,6
6	-	31,8	16	-	12,0	26	-	5,1	36	-	3,1	46	-	2,6
7	-	25,4	17	-	11,6	27	-	4,8	37	-	3,0	47	-	2,2
8	-	23,0	18	-	9,4	28	-	4,5	38	-	3,0	48	-	2,1
9	-	17,8	19	-	7,6	29	-	4,5	39	-	3,0	49	-	1,5
10	-	17,7	20	-	7,3	30	-	4,4	40	-	2,9	50	-	1,5

1) Постройте вариационный ряд, образовав 7-8 интервалов произвольно.

2) Рассчитайте средний размер выручки на одну фирму на основе средней арифметической, моды, медианы.

3) Рассчитайте показатели вариации.

4) Измерьте дифференциацию выручки на основе децильного коэффициента и коэффициента фондов.

5) Рассчитайте коэффициент концентрации Джини и Герфиндаля.

35. Имеются данные о распределении населения РФ по размеру среднедушевого денежного дохода в первом полугодии 2000 года:

Среднедушевой денежный доход, ден. ед.	Численность населения в % от общей численности
до 400	2,7
400,1-600,0	6,6
600,1-800,0	9,3
800,1-1000,0	10,1
1000,1-1200,0	9,9
1200,1-1600,0	16,9
1600,1-2000,0	12,6
свыше 2000,0	31,9
ВСЕГО:	100

Рассчитайте: 1) среднедушевой денежный доход на основе средней арифметической, моды и медианы;

2) показатели дифференциации концентрации.

[1] Использование коэффициента вариации имеет смысл при изучении вариации признака, принимающего только положительные значения. Совершенно неправильно пользоваться V в случае измерения колеблемости признака, принимающего как положительные, так и отрицательные значения. Не имеет смысла, например, V, вычисленный для изучения колеблемости среднегодовой температуры воздуха, что особенно ясно при среднегодовой температуре близкой к нулю.

[2] Существует много других аналитических выражений коэффициента Джини, но в целях экономии места мы остановимся на одном.

Дата: 2019-02-02, просмотров: 428.

⇐ Предыдущая 1 23