Справочные материалы
Пример 6.1. Рассмотрим два вариационных ряда:
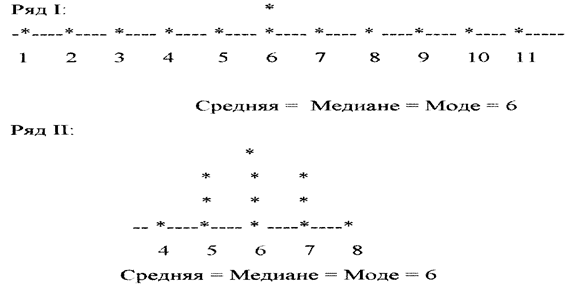
Ряд I: 1, 2, 3, 4, 5, 6, 6, 7, 8, 9, 10, 11.
Ряд II: 4, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 8.
В чем отличие между рядами, если 
?
|
Рис. 6.1. Сравнение вариации рядов I и II
|
Рисунок 6.1 графически изображает ряд I и ряд II. Ряд I более вариабелен, чем ряд II.
В статистике используется ряд мер вариабельности (колеблемости).
Определим интерквартильный размах как разницу между третьим и первым квартилями.
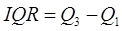(6.1)
Другая подобная мера – размах вариации.
Размах вариации в ряду – разность между наибольшим и наименьшим значениями признака.
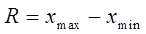(6.2)
По данным примера 6.1 имеем IQRI =5,5; IQRII =2; RI =10; RII =4.
Существуют и другие более часто используемые меры вариации. Это среднее линейное отклонение, дисперсия и стандартное отклонение (или среднее квадратическое отклонение).
Вариацию можно определить как меру отклонений значений признаков вариационного ряда от центра ряда распределения – средней арифметической.
Среднее линейное отклонение есть средняя арифметическая абсолютных значений отклонений значений признаков ряда от их средней арифметической.
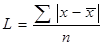– простое (6.3)
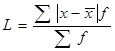– взвешенное (6.4)
Дисперсия вариационного ряда есть средняя арифметическая квадрата отклонения (средний квадрат отклонения) значений признаков ряда от их средней арифметической.
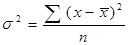– простая (6.5)
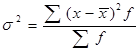– взвешенная (6.6)
Стандартное отклонение вариационного ряда есть арифметическое значение корня квадратного из дисперсии.
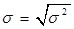(6.7)
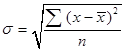– простое (6.7а)
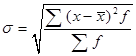– взвешенное (6.7б)
Для ручного счета лучше пользоваться формулой дисперсии следующего вида.
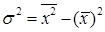(6.8)
Для оценки интенсивности вариации и сравнения ее в разных совокупностях и различных признаков применяются относительные показатели вариации, которые вычисляются как отношение абсолютных показателей силы вариации к средней арифметической. Существуют следующие показатели, выраженные в процентах: относительный размах вариации, относительное линейное отклонение и коэффициент вариации.
Относительный размах вариации (коэффициент осцилляции) отражает относительную меру колеблемости крайних значений признака вокруг средней.
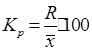(6.9)
Относительное линейное отклонение отражает долю усредненного значения абсолютных отклонений от средней величины.
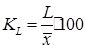(6.10)
Коэффициент вариации позволяет представить дисперсию как долю от средней величины.
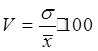, (6.11)
Чем меньше значение коэффициента вариации, тем однороднее совокупность по изучаемому признаку и типичнее средняя.[1]
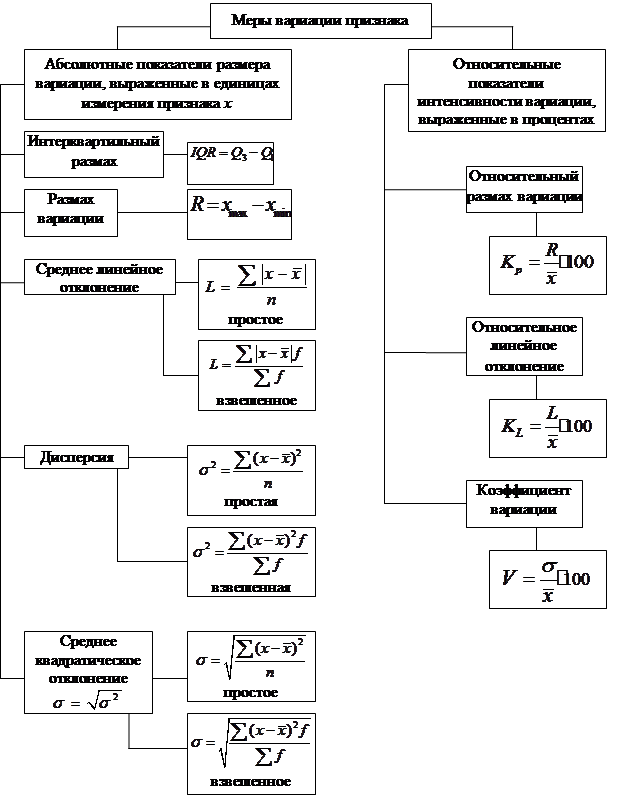
Для более ясного представления и использования в экономико-статистическом анализе показатели вариации представлены на схеме 6.1.
Правило сложения дисперсий
При изучении вариации для сгруппированных данных выделяют три вида дисперсий: общую дисперсию, внутригрупповую (частную) дисперсию, межгрупповую дисперсию.
Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов.
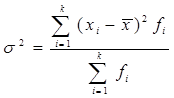. (6.12)
Схема 6.1
Статистическое изучение вариации
Справочные материалы
Пример 6.1. Рассмотрим два вариационных ряда:
Ряд I: 1, 2, 3, 4, 5, 6, 6, 7, 8, 9, 10, 11.
Ряд II: 4, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 8.
В чем отличие между рядами, если ?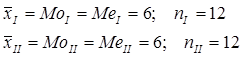
|
Рис. 6.1. Сравнение вариации рядов I и II
|
Рисунок 6.1 графически изображает ряд I и ряд II. Ряд I более вариабелен, чем ряд II.
В статистике используется ряд мер вариабельности (колеблемости).
Определим интерквартильный размах как разницу между третьим и первым квартилями.
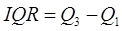(6.1)
Другая подобная мера – размах вариации.
Размах вариации в ряду – разность между наибольшим и наименьшим значениями признака.
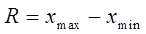(6.2)
По данным примера 6.1 имеем IQRI =5,5; IQRII =2; RI =10; RII =4.
Существуют и другие более часто используемые меры вариации. Это среднее линейное отклонение, дисперсия и стандартное отклонение (или среднее квадратическое отклонение).
Вариацию можно определить как меру отклонений значений признаков вариационного ряда от центра ряда распределения – средней арифметической.
Среднее линейное отклонение есть средняя арифметическая абсолютных значений отклонений значений признаков ряда от их средней арифметической.
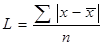– простое (6.3)
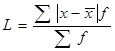– взвешенное (6.4)
Дисперсия вариационного ряда есть средняя арифметическая квадрата отклонения (средний квадрат отклонения) значений признаков ряда от их средней арифметической.
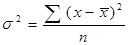– простая (6.5)
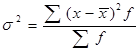– взвешенная (6.6)
Стандартное отклонение вариационного ряда есть арифметическое значение корня квадратного из дисперсии.
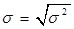(6.7)
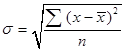– простое (6.7а)
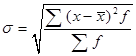– взвешенное (6.7б)
Для ручного счета лучше пользоваться формулой дисперсии следующего вида.
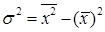(6.8)
Для оценки интенсивности вариации и сравнения ее в разных совокупностях и различных признаков применяются относительные показатели вариации, которые вычисляются как отношение абсолютных показателей силы вариации к средней арифметической. Существуют следующие показатели, выраженные в процентах: относительный размах вариации, относительное линейное отклонение и коэффициент вариации.
Относительный размах вариации (коэффициент осцилляции) отражает относительную меру колеблемости крайних значений признака вокруг средней.
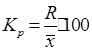(6.9)
Относительное линейное отклонение отражает долю усредненного значения абсолютных отклонений от средней величины.
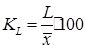(6.10)
Коэффициент вариации позволяет представить дисперсию как долю от средней величины.
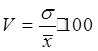, (6.11)
Чем меньше значение коэффициента вариации, тем однороднее совокупность по изучаемому признаку и типичнее средняя.[1]
Для более ясного представления и использования в экономико-статистическом анализе показатели вариации представлены на схеме 6.1.
Меры вариации для сгруппированных данных.
Правило сложения дисперсий
При изучении вариации для сгруппированных данных выделяют три вида дисперсий: общую дисперсию, внутригрупповую (частную) дисперсию, межгрупповую дисперсию.
Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов.
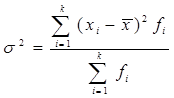. (6.12)
Схема 6.1
Статистическое изучение вариации
Дата: 2019-02-02, просмотров: 240.
