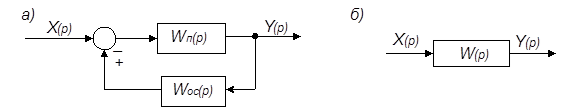
Найдем передаточную функцию W(p) звена (рис.4.4, б), эквивалентного встречно-параллельному соединению звеньев (рис.4.4, а).
Рис. 4.4. Алгоритмические схемы встречно-параллельного соединения звеньев (а)
и эквивалентного ему звена (б)
Передаточная функция соединения
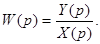 (4.3)
(4.3)
Но при этом
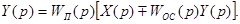 (4.4)
(4.4)
Здесь WП(p) и WОС (p) – передаточные функции соответственно прямой цепи и цепи обратной связи встречно-параллельного соединения звеньев.
После деления обеих частей равенства (4.4) на X(p) получаем
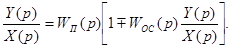 (4.5)
(4.5)
Учитывая соотношение (4.3) в равенстве (4.5), последнее приводим к виду
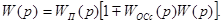 (4.6)
(4.6)
Решая уравнение (4.6) находим искомую передаточную функцию эквивалентного звена
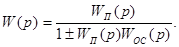 (4.7)
(4.7)
При отрицательной обратной связи передаточная функция эквивалентного звена
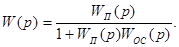 (4.8)
(4.8)
При положительной обратной связи передаточная функция эквивалентного звена
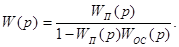 (4.9)
(4.9)
С помощью рассмотренных правил удается преобразовать (упростить) к простейшему виду (рис.4.4, б) любую алгоритмическую схему, не содержащую перекрестных связей между звеньями. Если же схема многоконтурная и содержит перекрестные связи, то эти правила можно применять лишь после устранения этих перекрестных связей. Для устранения перекрестных связей следует использовать ряд вспомогательных правил преобразований алгоритмических схем, которые приведены в табл. 4.1.
Таблица 4.1
Вспомогательные правила преобразования алгоритмических схем
| № | Операция | Исходная схема | Преобразованная схема |
| 1 | Перестановка узлов разветвления |
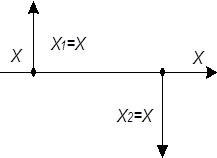
|
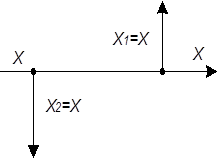
|
| 2 | Перестановка сумматоров |
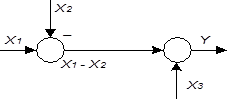
|
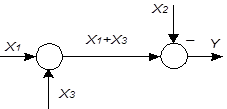
|
| 3 | Перенос узла разветвления через звено вперед |
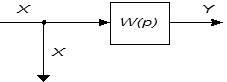
|
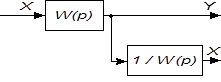
|
| 4 | Перенос узла разветвления через звено назад | 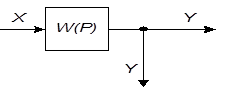
| 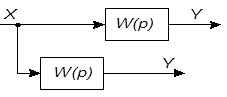
|
| 5 | Перенос сумматора через звено вперед |
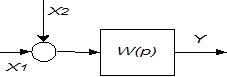
| 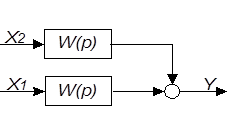
|
| 6 | Перенос сумматора через звено назад | 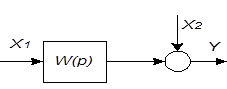
| 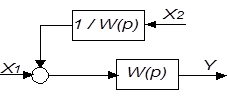
|
Пример применения правил преобразования алгоритмических схем
Преобразовать алгоритмическую схему АСУ (рис. 4.5, а), содержащую звенья с известными передаточными функциями, к схеме с одним эквивалентным звеном.
В табл. 4.2 приведена: информация после каждой операции преобразования.
Таблица 4.2
Операции преобразования
| № | Наименование операции преобразования | Передаточная функция эквивалентного звена | № рисунка с преобразованной алгоритмической схемой |
| 1 | Перенос сумматора В через звено 1 назад | 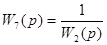
| 4.5, б |
| 2 | Перестановка сумматоров А и В | 
| 4.5, в |
| 3 | Замена параллельного соединения звеньев 2 и 4 | 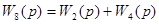
| 4.6, а |
| 4 | Замена последовательного соединения звеньев 1 и 8 | 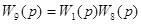
| 4.6, б |
| 5 | Замена последовательного соединения звеньев 6 и 7 | 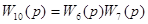
| 4.6, в |
| 6 | Замена встречно-параллельного соединения звеньев 5 и 9 | 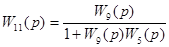
| 4.6, г |
| 7 | Замена последовательного соединения звеньев 3 и 11 | 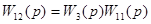
| 4.6, д |
| 8 | Замена встречно-параллельного соединения звеньев 10 и 12 | 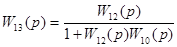
| 4.6, е |
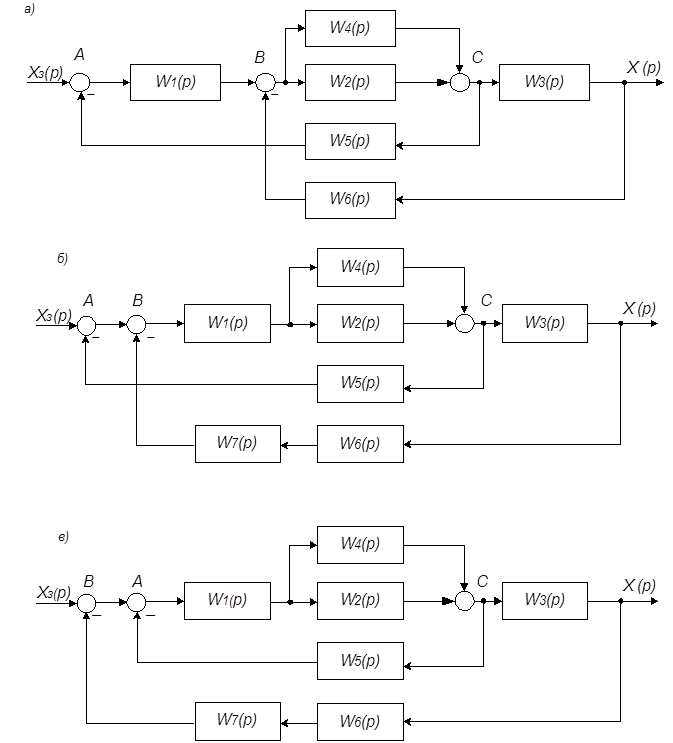
Рис. 4.5. Алгоритмические схемы АСУ
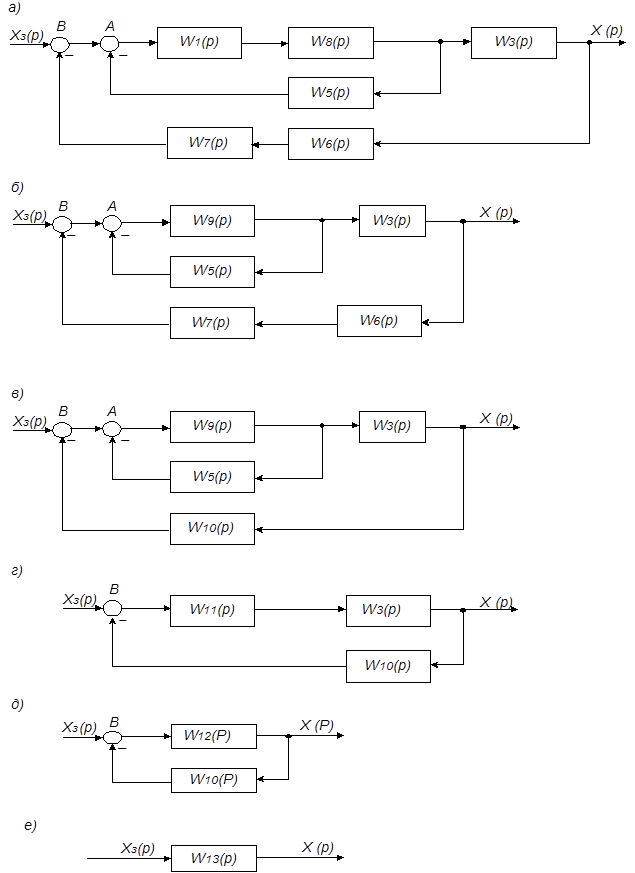
Рис. 4.6. Алгоритмические схемы АСУ
Дата: 2019-02-02, просмотров: 374.